基于改进海鸥算法优化支持向量机的斜拉桥索力优化研究

覃木宝 王华 王龙林

摘 要：针对大跨度斜拉桥斜拉索的索力优化问题，提出一种基于混合策略改进海鸥优化算法联合支持向量机的索力优化模型。融合折射反向学习、多方向螺旋攻击和非线性收敛等策略对标准海鸥优化算法进行改进，基于改进的海鸥优化算法（Improve Seagull optimization algorithm ，ISOA）對支持向量机（Support vector machine ，SVM）的惩罚因子和核函数参数进行优化，构建大跨度斜拉桥的索力组合-结构响应的预测模型，设计ISOA-SVM的索力优化流程并对考虑主梁线形控制下的斜拉索索力进行优化。结果表明，混合策略显著提高海鸥优化算法的收敛速度和收敛精度；采用ISOA参数优化后的SVM对数据样本具有良好的学习泛化能力，其测试集的平均相对误差（MRE）仅为1.08%，均方根误差（RMSE）仅为0.012 2；基于ISOA-SVM优化的索力组合有效改善了主梁线形和内力，主梁竖向挠度峰值降幅为36%，弯曲应力峰值降幅为11.94%，验证了该索力优化方法的有效性。

关键词：支持向量机；海鸥优化算法；非线性收敛；斜拉桥；索力优化

中图分类号：U448.27    文献标识码：A   文章编号：1006-8023（2023）04-0160-10

Research on Cable Force Optimization of Cable-stayed Bridges Based on

Improved Seagull Algorithm and Support Vector Machine

QIN Mubao1， WANG Hua2，3*， WANG Longlin3，4

（1.Guangxi Traffic Engineering Construction Guarantee Center， Nanning 530000， China; 2.School of Civil Engineering， Harbin

Institute of Technology， Harbin 150006， China; 3.Guangxi Communications Technology Group Co. Ltd.， Nanning

530000， China; 4.Transportation College， Jilin University， Changchun 130000， China）

Abstract：Aiming at the cable force optimization problem of long-span cable-stayed bridge， a cable force optimization method based on hybrid strategy improved seagull optimization algorithm and support vector machine is proposed. The standard seagull optimization algorithm is improved by integrating refraction reverse learning， multi-directional spiral attack and nonlinear convergence strategies. The penalty factor and kernel function parameters of support vector machine （SVM） are optimized by improved seagull optimization algorithm （ISOA）， and a prediction model of cable force combination structure response of long-span cable-stayed bridge is constructed. The cable force optimization model based on ISOA-SVM is designed and the cable force of stay cable under the control of girder alignment is optimized. The results show that the hybrid strategy significantly improves the convergence speed and convergence accuracy of seagull optimization algorithm. The SVM optimized by ISOA parameters has a good learning generalization ability for data samples. The average relative error of its test set is only 1.08%， and the root mean square error is only 0.012 2. The cable force combination based on ISOA-SVM optimization effectively improves the alignment and internal force of the main beam. The peak value reduction of the vertical deflection of the main beam is 36%， and the peak value reduction of the bending stress is 11.94%， which verifies the effectiveness of the cable force optimization method.

Keywords：Support vector machine; seagull optimization algorithm; nonlinear convergence; cable-stayed bridge; cable force optimization

收稿日期：2022-11-16

基金项目：广西科技计划项目（桂科AD19245152）；广西科技计划项目（桂科AB22035074）；南宁市创新创业领军人才“邕江计划”创新项目（2018-01-04）

第一作者简介：覃木宝，高级工程师。研究方向为大跨度桥梁受力分析与结构优化。E-mail： 302613279@qq.com

通信作者：王华，博士，高级工程师。研究方向为大跨度桥梁结构优化、智能优化算法的工程应用。E-mail： 962707235@qq.com

引文格式：覃木宝，王华，王龙林. 基于改进海鸥算法优化支持向量机的斜拉桥索力优化研究[J]. 森林工程， 2023，39（4）：160-169.

QIN M B， WANG H， WANG L L. Research on cable force optimization of cable-stayed bridges based on improved seagull algorithm and support vector machine[J]. Forest Engineering， 2023， 39（4）：160-169.

0 引 言

复杂结构的优化设计往往伴随着庞大的迭代次数和计算量，近年来，随着机器学习算法的不断开发与优化，部分专家学者将其作为代理模型应用于结构的优化设计中 [1]。徐文韬等[2]利用改进的遗传算法和BP神经网络建立了锅炉燃烧系统的多目标优化模型，通过对比不同优化模型的燃烧效率证明了所提方法的有效性；张德胜等[3]以立式离心泵为研究对象，针对离心泵的运行效率提出了基于神经网络和数值模拟的优化平台，研究结果表明神经网络算法可以准确构建优化设计变量和优化目标间的映射关系；梅益等[4]基于多目标优化的思想，采用遗传算法优化极限学习机模型对九轴五联动磨床结构进行了参数优化，验证了改进极限学习机在参数优化问题上的可行性。此外，还有部分专家学者针对各种实际问题提出了基于支持向量机（Support Vector Machine， SVM）的优化方法[5-7]，将机器学习算法不断推广应用于不同领域的优化问题中。

斜拉桥是大跨度桥梁中一种常见的结构形式，因其优美的造型和较强的跨越能力被广泛建设于河流航道中。斜拉桥的受力机理较为明晰，通过桥塔两侧的高强度钢绞线为主梁提供弹性支撑，从而减小主梁挠度和弯矩，因此斜拉索的受力和优化是大跨度斜拉桥工程设计中的研究重点之一。目前应用较广泛的大跨度斜拉桥索力优化方法是影响矩阵法和能量法[8]，但传统优化方法在进行索力优化时存在计算效率低、收敛精度差等局限性[9]，为避免这一现象的出现，部分专家学者将智能优化算法的相关理论引入索力优化问题中。张玉平等[10]基于多目标粒子群算法建立了斜拉桥的索力优化模型，根据Pareto最优解集求得了考虑多目标状态下的最优索力组合；占玉林等[11]采用响应面法联合粒子群算法对异性斜拉桥的索力优化问题进行了研究，得到了使主梁线形更合理的索力解；此外，还有一些专家基于群体智能算法对斜拉桥的索力优化展开了研究[12-14]。

综上所述，对于大跨度斜拉桥的索力优化问题，目前已有的研究多基于传统优化方法或群体智能优化算法，对于机器学习模型的引入较少，为进一步提升大跨度斜拉桥索力优化的效率，本研究提出一种基于混合策略改进海鸥优化算法联合支持向量机的索力优化方法，通过多种策略改进标准海鸥优化算法，构建参数优化的斜拉索力-结构响应预测模型，描述考虑主梁竖向挠度的索力优化数学模型，再次调用改进的海鸥优化算法对最优索力组合进行求解，所提方法可为类似工程结构的优化提供一定的参考。

1 支持向量机算法原理

支持向量机（SVM）是一种定义在特征空间上的机器学习算法，其基本工作逻辑为通过求取数据集中最大分类超平面完成关于损失函数优化问题的过程。对于非线性数据样本，SVM可以通过核函数将原样本数据映射至高维数据空间，在高维空间中将其转化为线性可分问题。故相较于其他机器学习模型，SVM对于小样本、非线性数据具有更高的适应性，SVM的基本原理如下[15]。

2.5 算法性能测试

为验证采用混合改进策略对海鸥优化算法（Improved Seagull Optimization Algorithm，ISOA）的有效性，引入标准海鸥优化算法、遗传算法（Genetic Algorithm，GA）、粒子群算法（Particle Swarm Algorithm，PSO）和麻雀搜索算法（Sparrow Search Algorithm，SSA）进行对比，种群规模N均设定为30，算法维数D均设定为30，最大迭代次数Tmax设定为500，算法独立运行50次。测试平台操作系统为Windows 10（x64），软件环境为MATLAB 2018b，中央处理器为Intel Core i7-8700 CPU@3.20 GHz，RAM為16 GB。选取单峰测试函数和多峰测试函数对各算法进行性能测试，各测试函数基本信息见表1。

考虑到算法性能对比的直观性，图4给出了各算法在不同测试函数下的收敛曲线。

由图4（a）可知，对于单峰测试函数Sphere，标准GA、PSO、SSA和SOA算法对其的收敛精度大致相同，均能收敛至理论最优值附近，各标准算法的寻优速度差距较小，在算法迭代全期保持了大致相同的收敛速度。观察ISOA收敛曲线，相较于其他标准算法，ISOA寻优能力得到明显提升，在约200次迭代后即完成理论最优解的寻优，寻优速度和精度均大幅高于其他算法。

由图4（b）可知，对于多峰测试函数Rastrigin，标准GA、PSO、SSA和SOA算法的收敛精度和速度差别较小，其中SSA和SOA提前陷入了局部极值，GA和PSO收敛速度较慢。ISOA算法表现出较高的寻优稳定性，算法前期以较高的效率收敛至全局最优解附近，并于300次迭代左右到达理论最优解。

由图4（c）和图4（d）可知，各标准GA、PSO、SSA和SOA算法对Ackley函数和Griewank函数的寻优效果存在一定的差异，PSO算法对Ackley函数的寻优效果不佳，但对Griewank函数的寻优表现优于GA、SSA和SOA；GA对Ackley函数的寻优精度高于另3种标准算法，但对Griewank函数的寻优表现较差。ISOA算法对Ackley函数和Griewank函数均表现出极高的寻优性能，寻优速度和精度方面大幅优于其他3种算法，且对于Griewank函数，在迭代过程中ISOA算法收敛曲线存在一定的停滞与波动，但整体呈现出较强的鲁棒性，相较于其他算法对局部极值的摆脱能力更强，极大避免了算法过早陷入局部最优解的情况。

结合不同测试函数的收敛曲线可知，混合策略对SOA算法的改进具有积极意义，ISOA算法在不同测试函数下均保持了较高的寻优性能，证明了改进策略的有效性。

3 基于ISOA-SVM的索力优化方法

核函数的选择对SVM的核心学习能力存在关键性影响，选择合适的核函数可以极大提高SVM对数据样本的学习泛化能力，目前SVM常用的核函数类型有线性核函数、高斯径向基核函数（Radial basis function ，RBF）、Sigmoid核函数和多项式核函数4种，由于RBF对于非线性数据的学习具有一定的优势，故研究选取RBF作为ISOA-SVM的核函数，RBF的表达式如公式（15）所示。

k（u，v）=exp（－‖x-x′‖22σ2）

=exp（-g‖x－x′‖2），g≥0。（15）

式中：σ为数据均方差；g为核函数参数。

为优化SVM的惩罚因子C和核函数参数g，首先建立大跨度斜拉桥的有限元数值计算模型，选取一次张拉扣挂的扣索索力作为输入变量，主梁挠度响应作为输出变量，建立输入变量和输出变量的样本集和测试集，通过SVM建立从输入变量到输出变量的映射关系，并采用ISOA算法对SVM的惩罚因子C和核函数参数g进行调优，使其预测精度达到预设精度以内。最后以结构弯曲应变能构造适应度函数，二次调用ISOA算法作为扣索索力求解器进行求解，得到考虑主梁挠度控制下的最优索力组合。主梁挠度响应如公式（16）所示。

U=1n∑ni=1Δui。（16）

式中：Δui为各索梁锚固处的挠度；i为挠度控制点序号；n为挠度控制点总数。

基于ISOA-SVM的索力优化方法求解流程如下。

3.1 基于参数优化SVM的结构响应预测模型

1）基于有限元数值模型计算结果生成结构输入

变量和输出变量的训练集和测试集，并进行归一化预处理。

2）初始化ISOA和SVM参数，将惩罚因子C和核参数g表征为海鸥在搜索空间中的坐标，计算适应度值。

3）更新海鸥位置并重新计算适应度值。

4）判断是否达到算法最大迭代次数或是否达到最优适应度，若是则输出当前最优参数组合，若不是则返回步骤3（图5）。

3.2 基于ISOA-SVM的索力优化模型

建立大跨度斜拉桥的索力优化数学模型如公式（17）所示。

FindX=[X1，X2，…，X34]T;

minU;

s.t. max（σ）≤[σmax]。（17）

式中：X为待优化索力组合；σ为斜拉索应力。

优化流程如下（图6）：

1）初始化ISOA参数，将索力向量表征为海鸥在搜索空间中的坐标。

2）基于优化后的SVM计算结构响应的适应度值。

3）更新海鸥位置并重新计算适应度值。

4）判断是否达到算法最大迭代次数或是否达到最优适应度，若是则输出当前最优参数组合，若不是则返回步骤3）。

4 工程算例

4.1 工程背景

某大跨度双塔双索面钢箱梁斜拉桥跨径布置为（182+450+182）m，设计荷载等级为公路Ⅰ级。桥塔采用C50混凝土浇筑，斜拉索采用高强度钢绞线，单侧索面布置68根斜拉索，主梁采用Q345qD钢材，桥型布置图如图7所示。

4.2 模型结果验证

采用MATLAB2018b平台及M语言编写斜拉桥索力-结构响应的SVM预测模型和ISOA的索力优化模型，实验环境配置见2.5节。

为验证ISOA-SVM模型计算结果的正确性，基于ANSYS APDL语言建立全桥的有限元数值计算模型。数值模型主梁钢箱梁采用Beam188梁单元进行模拟，斜拉索采用Link10杆单元进行模拟，主梁和斜拉索之间的刚臂采用MPC184单元进行模拟。采用ANSYS数值计算模型随机生成30组索力-挠度数据，其中20组作为训练集，10组作为测试集。有限元模型如图8所示。

引入未经优化的SVM模型、粒子群算法优化的SVM模型（PSO-SVM）、SOA优化的SVM（SOA-SVM）和ISOA优化的SVM模型（ISOA-SVM）进行对比，设置PSO、SOA、ISOA算法种群规模为40，最大迭代次数为500。测試集的挠度结果验证如图9所示，预测精度评价见表2。

对比不同算法优化支持向量机的目标变量预测结果与有限元模型的计算结果可知，未经参数优化的SVM对于不同测试集的拟合效果最差，MRE为48.41%；PSO-SVM、SOA-SVM预测精度大致相同，MRE约为25%；ISOA-SVM拟合效果最好，MRE仅为1.08%。对比各预测模型的RMSE，ISOA-SVM的预测精度远高于其他3种预测模型。测试集的结果表明，经混合策略改进的海鸥优化算法对支持向量机模型的参数寻优具有良好的适应性，ISOA-SVM对大跨度斜拉桥的结构响应预测具有较高的精度，验证了该预测模型的有效性。

4.3 优化结果分析

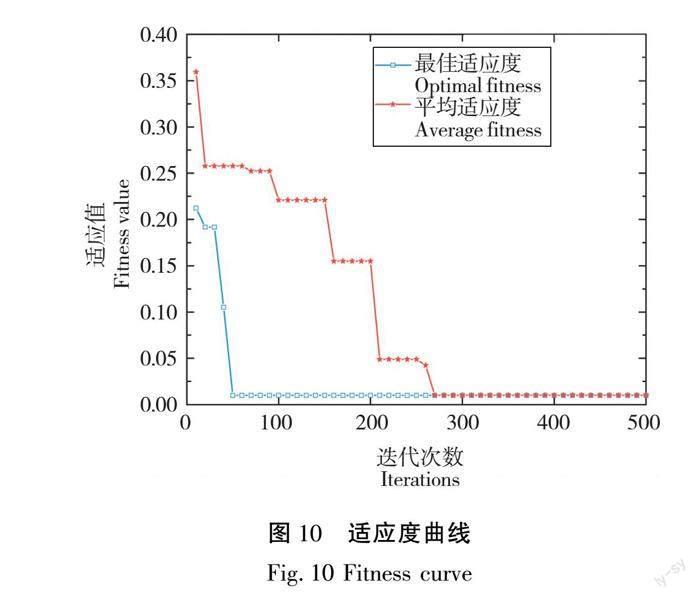
图10给出了ISOA索力寻优的适应度变化曲线，由图10可知，ISOA在第260次迭代左右收敛至全局最优，即视为ISOA算法寻得大跨度斜拉桥考虑主梁挠度控制下的最优索力组合，此时最佳适应度值为0.01。

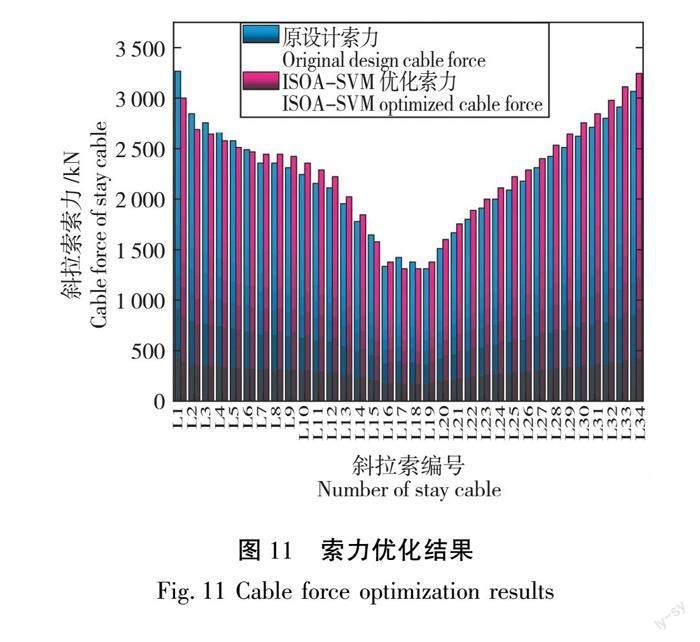
由于该斜拉桥左右桥塔沿中跨跨中呈对称布置，前后双索面受力特点相同，故取左侧单索面斜拉索进行分析，图11给出了恒载状态下原设计索力组合和基于ISOA-SVM算法优化后的索力组合。由图11可知，基于ISOA-SVM优化的索力组合与原设计索力组合分布趋势大致相同，各斜拉索强度系数均在安全系数范围之内，其中，L1—L6号、L15—L18

号扣索索力存在一定幅度的减小，L7—L14、L19—L34号扣索索力存在一定幅度的增加，索力整体均匀度得到小幅提升。

将ISOA-SVM计算得到的最优索力组合输入ANSYS有限元模型进行计算，取半结构进行分析，图12给出了优化前后恒载下的主梁竖向挠度曲线。由图12可知，采用ISOA-SVM优化后的索力组合计算得到的主梁竖向挠度得到显著改善，跨中位置竖向挠度大幅减小，主梁竖向挠度峰值由0.12 m下降至0.07 m，降幅约36%。恒载下的主梁线形更为合理，验证了考虑主梁挠度的ISOA-SVM索力优化模型的有效性。

图13给出了优化前后主梁钢箱梁截面的弯曲应力计算结果，由图13可知，采用优化索力计算得到的主梁钢箱梁截面峰值彎曲应力由62.97 MPa减小至55.45 MPa，降幅约11.94%，其余各截面弯曲应力均存在一定幅度的下降，可见优化索力在一定程度上降低了主梁钢箱梁截面的弯曲应力，主梁内力得到一定的改善。

5 结论

本研究针对大跨度斜拉桥索力优化的问题，提出了一种基于ISOA-SVM的索力优化方法，混合多种策略对SOA算法进行改进，通过对索力组合-结构响应样本数据的学习映射，建立了参数优化的SVM结构响应预测模型，采用ISOA算法对大跨度斜拉桥考虑主梁竖向挠度控制下的最优索力组合进行求解，得到结论如下。

1）提出了一种混合策略改进的海鸥优化算法。采用折射反向学习初始化、多方向螺旋攻击和非线性附加变量的改进方式可以明显提升海鸥优化算法的寻优性能，不同测试函数下的寻优结果表明，ISOA算法收敛速度更快，收敛精度更高。

2）基于ISOA参数优化后的SVM对结构响应的预测精度远高于未经优化的SVM和基于PSO、SOA优化的SVM，说明采用ISOA算法优化后的SVM对样本集数据的学习泛化能力更强，可以作为索力优化的代理模型进行计算。

3）以某大跨度斜拉桥为工程背景进行了应用研究，结果表明，ISOA算法对索力优化问题的收敛性良好，优化后的索力组合与原索力组合数值存在一定波动，但索力分布趋势大致相同；优化后主梁竖向挠度得到明显改善，跨中峰值挠度由0.12 m降低至0.07 m，降幅约36%；优化后主梁内力分布进一步优化，峰值弯曲应力由62.97 MPa减小至55.45 MPa，降幅约11.94%，说明了该索力优化方法的有效性。

【参 考 文 献】

[1]李昕光，元佳宇，王文超.基于均匀设计的电池组液冷结构多目标优化[J].电子测量技术，2022，45（13）：33-39.

LI X G， YUAN J Y， WANG W C. Multi-objective optimization of battery pack liquid cooling structure based on uniform design[J]. Electronic Measurement Technology， 2022， 45 （13）： 33-39.

[2]徐文韬，黄亚继，曹歌瀚，等.基于BP-改进NSGA-Ⅱ锅炉燃烧多目标优化[J].东南大学学报（自然科学版），2022，52（5）：943-952.

XU W T， HUANG Y J， CAO G H， et al. Multi-objective combustion optimization for boiler on BP-improved NSGA-Ⅱ[J]. Journal of Southeast University （Natural Science Edition）， 2022， 52 （5）： 943-952.

[3]张德胜，杨港，赵旭涛，等.基于BP神经网络的立式离心泵导叶与蜗壳优化设计[J].农业机械学报，2022，53（4）：130-139.

ZHANG D S， YANG G， ZHAO X T， et al. Optimization design of vane diffuser and volute in vertical centrifugal pump based on back propagation neural network[J]. Journal of Agricultural Machinery， 2022， 53 （4）： 130-139.

[4]梅益，薛茂远，甘盛霖，等.基于多目标的九轴五联动磨床整机分析与结构优化[J].湖南大学学报（自然科学版），2022，49（6）：25-36.

MEI Y， XUE M Y， GAN S L， et al. Whole machine analysis and structure optimization of nine-axis five-linkage grinder based on multi-objective[J]. Journal of Hunan University （Natural Science Edition）， 2022， 49 （6）： 25-36.

[5]唐捷，杨银，刘斯亮，等.基于改进SVM与NSGA-Ⅲ的台区相序在线优化方法[J].电力系统自动化，2022，46（3）：50-58.

TANG J， YANG Y， LIU S L， et al. On-line optimization method for phase sequence in station area based on improved support vector machine and non-dominated sorting genetic algorithm-Ⅲ[J]. Power System Automation， 2022， 46 （3）： 50-58.

[6]沈世斌，古翠红，钱伟行，等.基于SVM步态分类的柔性外骨骼自主定位优化方法[J].中国惯性技术学报，2020，28（2）：153-158.

SHEN S B， GU C H， QIAN W X， et al. Autonomous positioning optimization method of flexible exoskeleton robot based on gait classification by SVM [J]. Chinese Journal of Inertial Technology， 2020， 28 （2）： 153-158.

[7]张航，李洪双.结构优化设计的改进交叉熵支持向量机方法[J].西北工业大学学报，2018，36（3）：448-455.

ZHANG H， LI H S. Improved cross entropy support vector machine method for structural design optimization[J]. Journal of Northwest Polytechnical University， 2018， 36 （3）： 448-455.

[8]阴存欣.能量法和影响矩阵法相结合的斜拉桥成桥索力调整计算新方法及软件开发[J].建筑结构，2021，51（S1）：1532-1538.

YIN C X. New method for adjustment and calculation of cable forces of cable-stayed bridges and software development compounding bending energy method and effect matrix method[J]. Building Structure， 2021， 51 （S1）： 1532-1538.

[9]马广.基于混合遗传算法的四线钢桁斜拉桥索力优化研究[J].铁道标准设计，2020，64（S1）：85-89.

MA G. Study on cable force optimization of steel truss cable stayed bridge carrying four rail tracks based on hybrid genetic algorithm [J]. Railway Standard Design， 2020， 64 （S1）： 85-89.

[10]张玉平，刘雪松，李传习.基于MOPSO算法的斜拉桥索力优化分析[J].土木与环境工程学报（中英文），2020，42（2）：107-114.

HANG Y P， LIU X S， LI C X. Optimization of cable tension of cable-stayed bridges based on multi-objective particle swarm optimization algorithm[J]. Journal of Civil and Environmental Engineering （Chinese and English）， 2020， 42 （2）： 107-114.

[11]占玉林，侯之瑤，邵俊虎，等.基于响应面法及粒子群算法的异形斜拉桥索力优化[J].桥梁建设，2022，52（3）：16-23.

ZHAN Y L， HOU Z Y， SHAO J H， et al. Cable force optimization of irregular cable-stayed bridge based on response surface method and particle swarm optimization algorithm[J]. Bridge Construction， 2022， 52 （3）： 16-23.

[12]康俊涛，齐凯凯，张亚州.基于信息共享猴群算法的混合梁斜拉桥索力优化[J].公路工程，2020，45（3）：1-7，28.

KANG J T， QI K K， ZHANG Y Z. Optimization of cable force for cable-stayed bridge with mixed stiffening girders by using information exchange based monkey algorithm [J]. Highway Engineering， 2020， 45 （3）： 1-7，28.

[13]朱敏，刘荣桂，谢桂华，等.基于多种群遗传算法的大跨度斜拉桥索力优化[J].世界桥梁，2016，44（3）：38-42.

ZHU M， LIU R G， XIE G H， et al. Cable force optimization for long-span cable-stayed bridge based on multi-population genetic algorithm[J]. World Bridge， 2016， 44 （3）： 38-42.

[14]孙宇飞，郑晓雯，陈浩，等.基于改进遗传算法的颚式破碎机优化方法研究[J].哈尔滨理工大学学报，2022，27（2）：29-35.

SUN Y F， ZHENG X W， CHEN H， et al. Optimization of jaw crusher based on improved genetic algorithm[J]. Journal of Harbin University of Science and Technology， 2022， 27（2）： 29-35.

[15]郭小萍，尹瑞琛，李元.基于MDP-SVM的过程多类型故障诊断[J].电子测量技术，2022，45（1）：159-164.

GUO X P， YIN R C， LI Y. Process multi-type fault diagnosis based on MDP-SVM[J]. Electronic Measurement Technology， 2022， 45 （1）： 159-164.

[16]GAURAV D， VIJAY K. Seagull optimization algorithm： theory and its applications for large-scale industrial engineering problems [J]. Knowledge-Based Systems， 2019， 165： 169-196.

[17]李爱莲，全凌翔，崔桂梅，等.融合正余弦和柯西变异的麻雀搜索算法[J].计算机工程与应用，2022，58（3）：91-99.

LI A L， QUAN L X， CUI G M， et al. Sparrow search algorithm combining sine-cosine and cauchy mutation[J]. Computer Engineering and Applications， 2022， 58 （3）： 91-99.

[18]周蓉，李俊，王浩.基于灰狼优化的反向学习粒子群算法[J].计算机工程与应用，2020，56（7）：48-56.

ZHOU R， LI J， WANG H. Reverse learning particle swarm optimization based on grey wolf optimization[J]. Computer Engineering and Application， 2020， 56 （7）： 48-56.

[19]張冰洁，何庆，戴松利，等.多方向螺旋搜索的混沌海鸥优化算法[J].小型微型计算机系统，2023，44（3）：536-543.

ZHANG B J， HE Q， DAI S L， et al. Multi-directional exploring seagull optimization algorithm based on chaotic map[J]. Small Micro Computer System， 2023， 44 （3）： 536-543.

[20]刘亮，何庆.基于改进蝗虫优化算法的特征选择方法[J].南京大学学报（自然科学），2020，56（1）：41-50.

LIU L， HE Q. An feature selection method based on improved grasshopper optimization algorithm[J]. Journal of Nanjing University （Natural Science）， 2020， 56 （1）： 41-50.