基于FAHP-熵权理论的康复轮椅方案决策灰色评估
2023-08-07杨昕妍张继娟谭雨婕张仲凤
杨昕妍 张继娟 谭雨婕 张仲凤
(1.中南林业科技大学家具与艺术设计学院,湖南 长沙 410004;2.国家林业和草原局绿色家具工程技术研究中心,湖南 长沙 410004;3.湖南省绿色家居工程技术研究中心,湖南 长沙 410004)
自2001 年始,康复工程及公共服务体系快速建立,至“十三五”期间,康复器械适配率超80%[1-2]。2021 年我国残疾人口达8 500 万[3-4],设计研究康复辅助器械是发展趋势[5],目前有关康复轮椅的研究多是进行改良设计[6],新型产品研发成本高、迭代慢,康复效果有待考究[7-8],因此,提高康复产品使用率及适配性是必要的。
辜俊丽[9]利用AHP(Analytic Hierarchy Process)与TRIZ(Theory of the Solution of Inventive Problems)结合实现对残障人轮椅方案设计。周清华[10]通过TOPSIS获得老年代步车方案。Yue等[11]通过AHP对老年家庭医疗产品进行设计评价。刘征宏[12]通过数控机床产品方案验证了TOPSIS和灰色关联分析法的有效性。本文通过灰色关联法[13]、层次分析法和熵权法对轮椅方案进行评价及优选,以提高决策效率。构建产品设计的评价体系标准有助于实现产品创新[14]。
1 康复轮椅方案决策评估体系构建
1.1 康复轮椅设计原理
人体共206块骨骼,由关节和韧带连接。相互牵引而运动。下肢骨包括髋骨、腓骨、肢骨等,上肢包含肩胛骨、肱骨、桡骨等[10]。中枢神经控制关节运动,当其被破坏时,可采取按摩等手段辅助治疗。本研究参考Salter教授的连续被动运动(Continuous Passive Motion,CPM)理念,设计能有效提高用户因久坐导致的神经功能受损恢复能力的座椅。利用康复器械训练有三个阶段[15],即前期被动运动、中期辅助主动运动、后期阻抗运动。前两个阶段为防止肌力退化,后期为加速提高恢复 效果。
1.2 康复轮椅方案决策评估体系
根据调研,确定康复轮椅方案决策评估指标为康复功能指标、智能控制指标、安全载荷指标、模块性能指标和情感交互指标。基于互质原则得到康复轮椅设计决策评估体系,构建完善的康养产业标准体系是必要的[16],如图1 所示。

图1 康复轮椅方案决策评估体系Fig.1 Decision evaluation system for rehabilitation wheelchair program
该评估过程中,不同评估方法可能会得到不同评估结果,为保证结果准确,采用基于灰色关联分析法的主客观综合权重评估方法[17],如图2 所示。

图2 基于AHP-熵权理论的灰色评估Fig.2 Grey evaluation based on AHP-entropy weight theory
2 基于FAHP-熵权理论的灰色评估
2.1 灰色关联分析法步骤
根据所构建的康复轮椅评估体系图,被评估方案为C(C=1,2,3,n),评估一级指标的集合为E'=(E'J),评估二级指标的集合为E'={E'1m,E'2m,E'3m...E'nm},则评价步骤为:
2.1.1 确定参考数据列
将各指标最优值确定为参考数据列,将参考数据列定为E'0=(E'01,E'02,E'03...E'0m)。
2.1.2 数据无量纲化
为提高数据有效性,将不同指标按公式(1)和(2)进行归一化处理。将评估指标分为经济型指标和经济性指标[18],成本型指标参考,E0k=min(E1k,E2k,...,Emk,),经济性指标E0k=max(E1k,E2k,...,Emk,)处理后得到比较矩阵E=(E'Jk)mn=(J=[1,m];k=[1,n])
式中:J=1,2,3,...,n;k=1,2,3,...,m。进行无量纲化处理后构成加权矩阵Enm。
2.1.3 确定极值和极差
2.1.4 计算关联系数
关联系数表示比较序列与参考序列在某一值上的关联性,根据公式(5)计算关联系数,其中,ρ越小,则关联系数间差异性越强[19]。
式中:ρ为分辨系数。
2.1.5 计算关联序
计算各指标与参考序列在某一值上关联系数的平均值,其中,ξJk为比较序列与参考序列的关联度;m为评价指标数目。
2.2 FAHP-熵权法综合权重计算
层次分析法是美国运筹学家Saaty提出的系统分析方法[20]。该模型通过将基础单元按相互支配关系分为递进层次结构,再通过两两比较确定重要性[21]完成定性指标的定量评估。某一指标的信息熵越小,则该指标所能提供的信息量就越大,在综合评价中所起作用越大,表示权重越高[22-23]。
2.2.1 建立判断矩阵
采用9分制标度法为各评估指标进行两两比较打分,建立判断矩阵A'={A1m,A2m,A3m...Anm}。
2.2.2 计算主观权重
(1)计算相对权重
计算每行的标度乘积,后判断其几何平均值:
(2)计算相对权重:
(3)计算各评估指标最大特征值[24]:
式中:aJn为向量aJ第n个分量,n为阶数。
(4)一致性检验[25],计算一致性比值:
式中:RI为平均随机一致性指标;CR为一致性比值。CR≤0.1表明一致性检验合格,反之,则不合格[26]。
2.2.3 计算客观权重
(1)将评分矩阵转换为归一化矩阵
对矩阵中各项评估指标按公式进行归一化处理:
式中:PJk为归一化决策矩阵,bJk为原始矩阵数值,J=1,2,...,m,k=1,2,...,n。
(2)确定各评估指标的熵
计算第k项指标的熵值:
式中:Yk为各指标信息熵,Yk越小代表k指标下的数据离散程度越高,所提供信息量越大。
(3)定义了k个指标的熵后,可得到熵权如下[17]:
式中:ωk为第k个指标的熵权,且有
2.3 灰色加权综合权重计算
按公式(15)计算各指标与参考序列在某一值上关联系数的平均值:
式中:ξJk为比较序列与参考序列的关联度;m为评价指标数目。
按公式(16)计算灰色加权关联度并排序,排名靠前的方案即为优选方案,设计方案中指标权重高且得分较低的指标需优化程度高。
式中:ωk为第k项评估指标的权重值;ξJk为第J个产品的第k项评估指标与参考序列的关联度[27]。
3 康复轮椅案例验证
3.1 数据获取
本研究分两组调研对象,一组为业余组,一组为专家组。业余组由20名患者组成,专家组由5名康复器械专家、5名按摩医生、5名主攻康复产品设计硕士研究生和5名机械设计硕士研究生组成,并对三款康复轮椅方案进行测试打分,方案如图4所示。情感交互指标参考图3进行评估,专家组所产生分数的均值为方案评估最终得分,形成比较矩阵E。
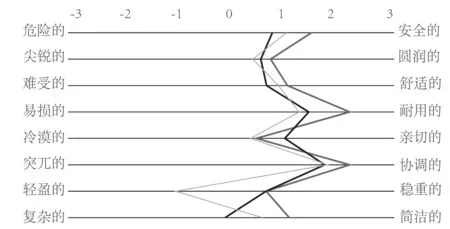
图3 业余组情感交互指标感性评价结果Fig.3 Emotional interaction index perceptual evaluation results of amateur group
3.2 计算关联度
将各项评估指标最优解定为参考序列,即,(E0)=(5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5),确定关联系数中ρ的取值为0.5[20]。计算关联系数公式中,ρ越小,分辨力就越大,一般ρ的取值区间为(0, 1),根据评价对象进行取值。当ρ≤ 0.546 3时,分辨力最好,一般取ρ= 0.5。利用SPSS23统计分析软件进行数据分析,关联系数计算结果如表1所示,三个方案关联度为:C1=0.729,C2=0.697,C3=0.794。

表1 关联系数计算结果Tab.1 Calculation result of correlation coefficient
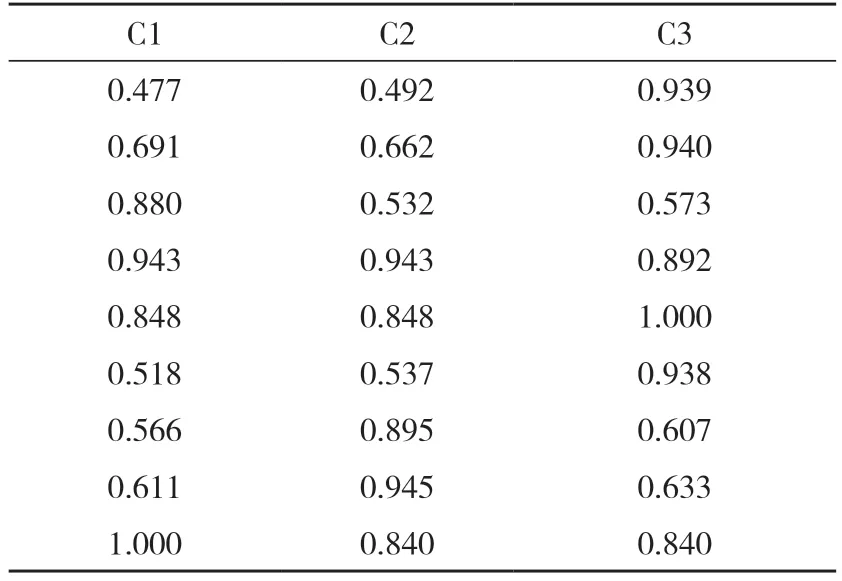
(续表1)
3.3 FAHP-熵权理论综合评价步骤
3.3.1 FAHP-熵权理论权重计算
将康复轮椅评估体系中一级指标作为准则层,二级指标作为方案层。根据专家组对各个评估指标的打分,形成5个矩阵主客观权重[12],如表5所示。
3.3.2 计算综合权重
层次分析法结合熵权法的综合权重采用公式ω=τω1+(1-τ)ω2计算,结果如表2所示。

表2 综合权重计算结果Tab.2 Calculation result of comprehensive weight
根据公式(16)计算灰色加权关联度,并按照结果进行排序,结果C1=0.161 5,C2=0.154 9,C3=0.167 3,排序后为C3>C1>C2。
3.4 设计评价验证
选取当地某老年康复医院中50位不同程度上下肢功能障碍人群、30位半自理老人和20位护工。采用李克特五级量表法评价,所得分值和满意度呈正相关。共有效回收98份,有效率98%。利用SPSS23软件进行信效度检验,信度Alpha系数为0.639,大于0.7,说明信度可靠,KMO值为0.605(KMO≥0.6),P为0.000(P≤0.05),说明效度较好。得到康复轮椅方案C3>C1>C2,符合表3中灰色加权关联度结果,说明该决策流程有效。

表3 综合权重表Tab.3 Comprehensive weight table
4 结论
本文通过构建康复轮椅设计评估体系,有效提高了设计效率。综合运用模糊层次法、熵权法、灰色关联法,能够快速准确地得到合理方案。三款肢体康复轮椅设计方案关联度为0.161 5、0.154 9 和0.167 3,第三款方案得分最高。经问卷调研后,验证方案三为最优设计,与多层级综合评价结果一致。本文所提出的评估体系和评价流程可以为相关康复辅具设计提供创新参考。
