基于灰狼算法优化支持向量回归模型的木材染色配色算法研究
2023-08-07管雪梅杨渠三
管雪梅 杨渠三 吴 言
(东北林业大学机电学院,黑龙江 哈尔滨 150040)
木材作为常见的建筑材料,被广泛应用于工业生产中。在禁止天然林商业性采伐之前,为了经济发展而牺牲林业资源,导致林业资源消耗过大[1-3]。木材染色对解决这一问题具有极其重要的作用[4-8]。计算机配色为木材染色提供了许多优异的方法[9-12]。将计算机配色应用到木材染色中,可以加快染色配方的生成速率,提高染料配比的准确度。近年来,越来越多的研究者将神经网络和深度学习模型应用到木材配色中,并取得了较多成果。反向传播(BP)神经网络在预测精度和泛化能力上存在很大缺陷,若用粒子群算法对其进行优化,将会提高预测效果。然而,受限于样本数量,其收敛速度不理想[13]。将K值聚类算法融合径向基(Radical Basis Function)神经网络,可进一步提高其配色精度,配色速度也会更快[14]。用粒子群优化Friele光学模型,平均拟合色差明显提高[15]。将全光谱配色融入Friele算法,将能有效改善色差均值[16]。对Stearns-Noechel模型中的参数M循环赋值,可进一步减小其拟合色差[17]。采用粒子群算法( PSO )对Stearns-Noechel模型进行优化,精度和速度都有所提高[18]。
目前针对智能配色已开展了很多研究,提高配色精度始终是研究人员不断追求的目标。鉴于支持向量回归(SVR)法具有很强的泛化能力,且容易实现,在各种预测中均有出色的表现[19]。本文基于SVR建立预测模型,并用灰狼算法进行优化,对灰狼算法(Grey Wolf Optimization)算法的不足加以改进[20],以光谱反射率作为输入,染色配比作为输出,可以减小配色误差,提高生产效率,从而推动木材染色技术的发展,实现人工速生材的高值化利用。
1 材料与方法
1.1 试验材料
樟子松(Pinus sylvestrisvar.mongolica Litv)旋切单板,并加工成40 mm×60 mm×0.5 mm的尺寸,用于染色处理。漂白剂(H2O2溶液),染色材料包括活性红(X-3B)染料、活性黄(X-RG)染料和活性蓝(X-3G)染料,染色助剂包括渗透剂(水性JFC溶液)、固色剂(无水碳酸钠)、促染剂(NaCl)等,材料购置于北京化工厂。
1.2 试验设备
芬兰SPECIM高光谱分析仪、数显恒温水浴锅(上海力辰邦西仪器科技有限公司)、电子天平、烧杯、202-Ⅰ型电热恒温干燥箱(天津泰斯特仪器公司)。
1.3 染色处理
为消除木材本身颜色的影响,染色前对试样进行漂白处理。配置浓度为4%H2O2漂白液500 mL,加入 7.5 g Na2SiO3后搅拌均匀,放入试样,设置浴比为1∶20,在65 ℃水浴锅中静置2 h。漂白结束后,用清水冲洗试样,并进行干燥。
干燥后,用蒸馏水配置500 mL的染液,染液中加入浓度为1 g/L的渗透剂JFC与15 g/L的NaCl,将三种染料按照设置的染料浓度分别加入,搅拌均匀后将漂白试样放入其中,在65 ℃水浴锅中静置2 h。然后加入20 g/L的Na2CO3固色30 min,结束后,用清水冲洗染色单板表面,并进行干燥,使其含水率降至8%,本文共设计120组染料浓度配比,每组6个木材单板试样,共计720个染色单板。部分染料浓度如表1所示,部分染色单板如图1所示。

图1 染色后部分木材单板照片Fig.1 Pictures of partial wood veneer after dyeing
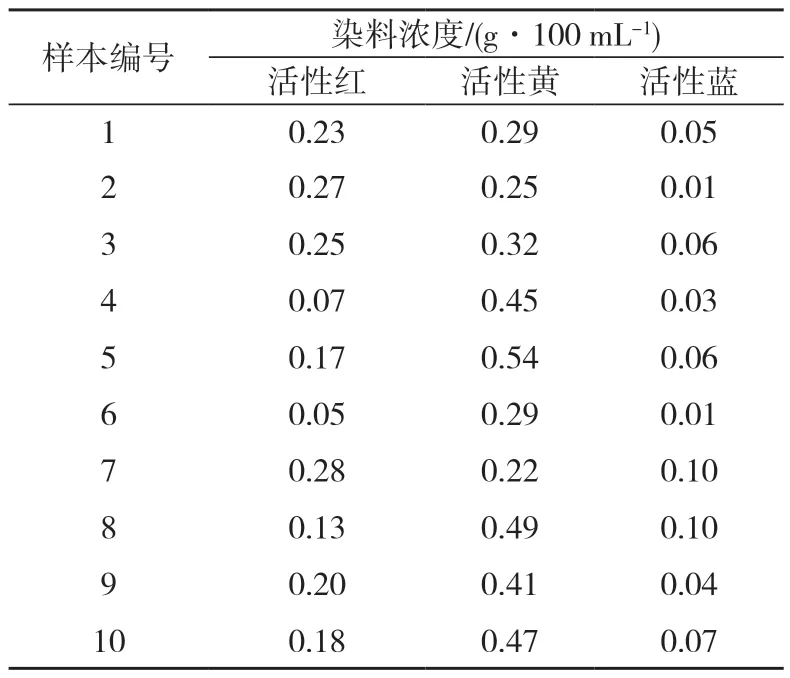
表1 部分木材单板染液染料配比Tab.1 Dye ratio of partial wood veneer dyeing solution
采用高光谱分析仪对染色后的木材单板进行光谱反射率提取,得到单板在400~700 nm波段各波长的光谱反射率,每隔20 nm取一个波长,共16个波长。部分染色单板各波长的光谱反射率如表2所示。
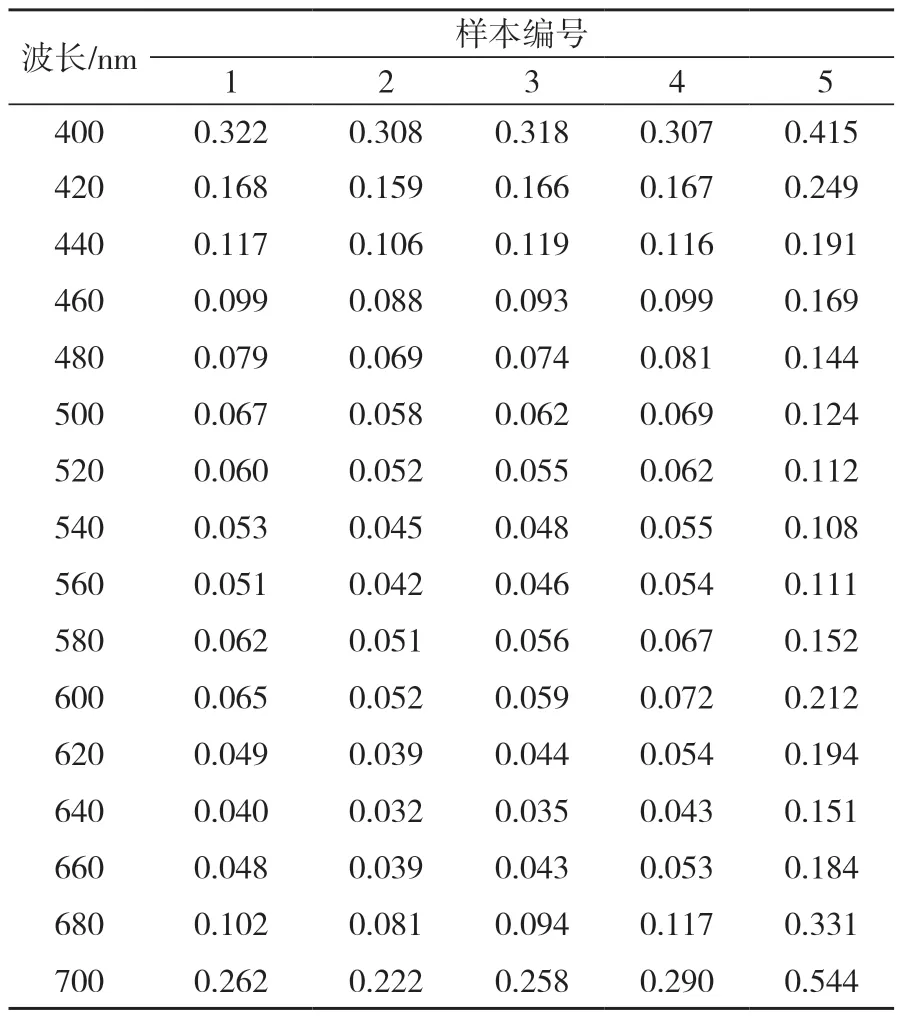
表2 部分样本不同波长对应的光谱反射率Tab.2 Spectral reflectance corresponding to different wavelengths of some samples
2 研究方法
2.1 SVR基本原理
SVR是支持向量机(SVM)的一个应用分支[21],但两者有明显不同。SVR的样本点只有一类,找到一个超平面使得所有样本点距离该超平面距离最近,从而达到拟合的目的。即给定样本集合:
笔者希望得到形如
的回归模型,使得f(x)和y趋近一致。
在SVR中允许存在偏差ε,当|y-f(x)|≤ε时定义该模型无损失,如图2 所示。当样本数据在虚线外时,|yf(x)|>ε定义为有损失,损失函数为|y-f(x)|-ε。根据图2可知,当ε变大时,模型的灵敏度降低,会导致“欠学习”问题,ε过大会导致“过学习”。
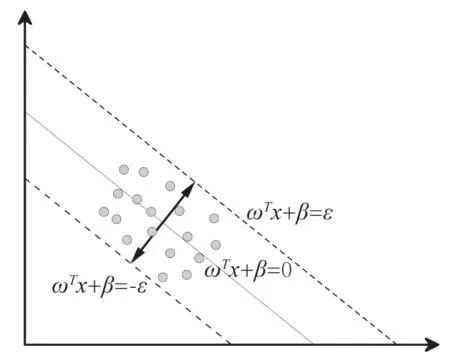
图2 SVR原理Fig.2 Schematic diagram of SVR algorithm
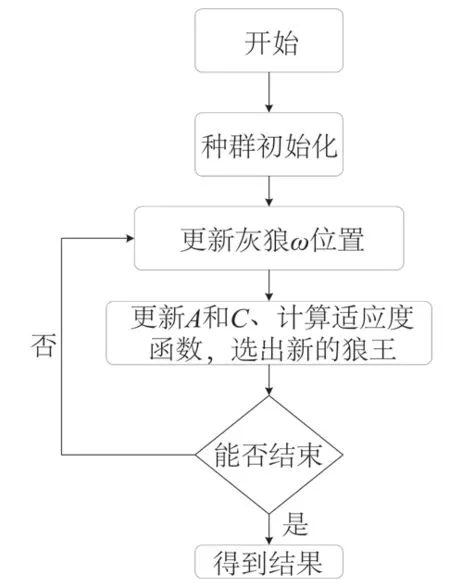
图3 灰狼算法原理Fig.3 Grey wolf algorithm principle
在SVR中还有两个参数分别是惩罚系数C和gamma。C代表对误差样本的宽容度,当C过大时,对误差容忍小,容易过拟合,反之易陷入欠拟合。gamma是选择RBF函数作为核函数自带的参数,gamma决定支持向量的数目,影响训练速度[22]。对于SVR的改进即对此三个参数进行寻优。
2.2 灰狼算法基本原理
灰狼算法来自于灰狼群体捕猎行为,将灰狼捕猎时的位置类比于求解问题中的可行解,狼群可以分为四部分,分别是α狼、β狼,δ狼和ω狼。在算法中,由α狼、β狼,δ狼作为引导,狼群中的个体会向着位置最优的三个个体移动[23]。数学描述如下:
1)包围。灰狼会向着头狼前进,计算其位置;
式中:XP(t)为t代时猎物位置;X(t)为t代灰狼位置;r1、r2是取值在[0,1]内的随机向量。随机数C决定了灰狼位置与猎物的距离,随着不断迭代,该灰狼位置与猎物之间的距离会趋于减小。
2)狩猎。设α狼、β狼,δ狼的位置为X1、X2、X3,迭代过程中用α狼、β狼,δ狼指导ω狼的移动,那么根据α狼、β狼,δ狼的位置和式(5)得出的三个位置为X1、X2、X3,灰狼ω将要移动到的位置为:
可以看出,A决定向目标位置靠近还是向目标位置远离。所以只有当|A|≥1,才有更好的全局搜索能力。为此,a采用以下公式进行计算,
式中:t为当前迭代次数;T为设置最大迭代次数;可知a的取值范围为[0,2],且递减。a值增大时,|A|≥1,狼群在此时进行全局搜索寻优;a值减小时,|A|≤1,狼群将在小范围内进行局部寻优。
2.3 改进灰狼算法
群体中灰狼个体的寻优过程对该算法的收敛速度和预测精度有较大的影响,同大部分算法一样,灰狼算法也存在会陷入局部最优解的缺点,为解决这一问题需要对灰狼算法进行改进[24-25]。
2.3.1 优化收敛因子
由上可知,当|A|≥1时,狼群进行全局搜索寻优;当a值减小时,|A|≤1,狼群将在小范围内进行局部寻优;A的大小又取决于a,传统的灰狼算法中,这是一个线性递减变化,但这种线性递减方式在实际寻优过程中不符合寻优规律,在寻优过程中容易陷入局部最优[26-28]。为改进这一问题,本文对a提出一种非线性收敛方式:
a随迭代次数变化曲线如图4所示。由图可知,a改为非线性函数后,在a较大时,衰减程度比较低;在a较小时,衰减程度比较高,能有效避免陷入局部最优。

图4 a值变化曲线Fig.4 a-value change curve
2.3.2 改进位置更新策略
原始的灰狼算法位置更新公式为式(6),初始化得到三只头狼(α狼、β狼、δ狼)的位置会被保存,然后在迭代过程中根据式(6)不断更新个体位置,直至能够出现适应度值更小的灰狼个体。未出现适应度更优异的个体之前,其他灰狼始终以这三只灰狼为目标前进。文献[25]提出了一种自适应位置更新策略。在此基础上,本文提出一种寻优效果更好的位置自适应策略:
另外,三只头狼的位置在更新位置时的重要程度不同,引入基于指导位置的动态比例权重:
则式(14)为:
2.4 基于IGWO-SVR的染色智能配方预测模型的建立
2.4.1 确定模型输入和输出
在传统的计算机配色中,常选用三刺激值作为输入,但是容易出现“同色异谱”现象,而一种颜色的光谱反射率曲线在固定光照条件下是唯一的,将其作为输入能够很好地避免这一现象。因此,笔者选择以各波长的光谱反射率为输入,三种染料的配比作为输出。
2.4.2 融合IGWO和SVR
灰狼算法优化原理是利用算法中的寻优能力对SVR中的参数进行不断赋值,从而找到达到最好预测效果的参数,该模型的原理如图4所示,具体步骤为:
1)读取制作好的染料配比和光谱反射率数据,对数据进行归一化处理,以光谱反射率作为输入,染料配比作为输出;
2)SVR参数寻优,将每只灰狼个体位置设置为xi=[Ci,εi,gammai],赋值后在样本集上训练,适应度函数选取预测值与真实值的均方误差,将误差最好的灰狼位置保留,然后根据式(14)更新灰狼位置,并不断重复计算适应度,与之前的适应度进行对比,根据设置好的迭代次数进行迭代,当超过最大迭代次数时,结束学习过程,并得到位置最好的灰狼(位置)。
3)将2)中得到的三个[C,ε,gamma](最优位置)带入SVR模型,运行SVR程序训练数据并对测试集进行预测,将数据反归一化后输出。因为配方浓度较小,采用的评价指标为配方相对偏差,配方相对偏差公式为:,yi(i=1,2,3)为测试样本真实配比,pi(i=1,2,3)为测试样本预测染料配比。
本研究对灰狼算法设置参数种群规模为50,狼群寻值(C、ε、gamma)范围为[0,100],最大迭代次数设置为500。
3 模型的性能测试与结果分析
为了验证IGWO算法的优越性,采用IGWO算法与传统GWO算法分别对SVR模型进行优化。算法在迭代过程中适应度值随迭代次数变化的曲线如图5所示。IGWO-1为引入非线性收敛因子适应度值变化曲线,IGWO-2为改进位置更新策略适应度值变化曲线,IGWO为引入收敛因子和融合位置更新策略并引入自适应权重的适应度值变化曲线。对比曲线可以看出,IGWO收敛速度和精度都有明显提高,说明改进后的IGWO对SVR进行优化是合理的。

图5 IGWO-SVR原理图Fig.5 IGWO-SVR schematic diagram
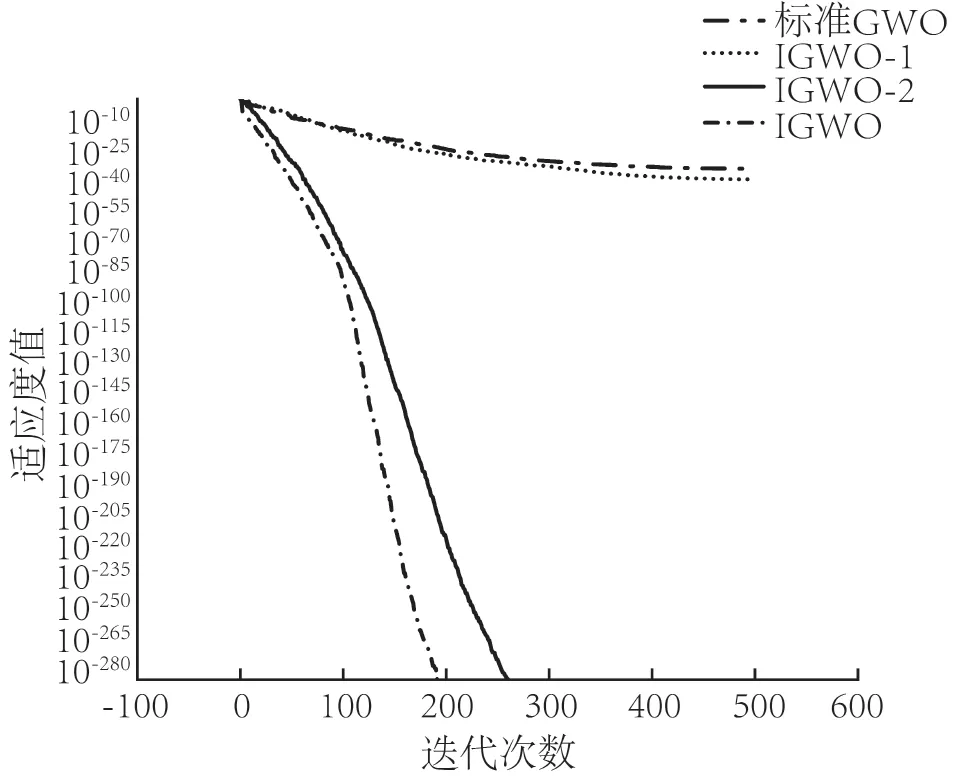
图6 不同GWO的适应度值变化曲线Fig.6 Variation curve of fitness value of different GWOs
利用Python验证模型预测能力。选取的测试集样本染料配比情况如表3。

表3 选取的10 组测试集数据Tab.3 Selected 10 groups of test set data
为进一步验证IGWO对于SVR优化的优越性,用IGWO-SVR对模型进行预测,并与标准SVR和GWOSVR的预测结果进行比较。无优化的SVR模型对配方进行预测时,根据经验和手动寻优对SVR参数设置为C=10,ε=0.1,gamma=1,得到的预测结果如表4 所示。用GWO-SVR进行预测时,设置的种群规模,狼群寻值范围和迭代次数与IGWO-SVR相同,预测结果如表5所示。
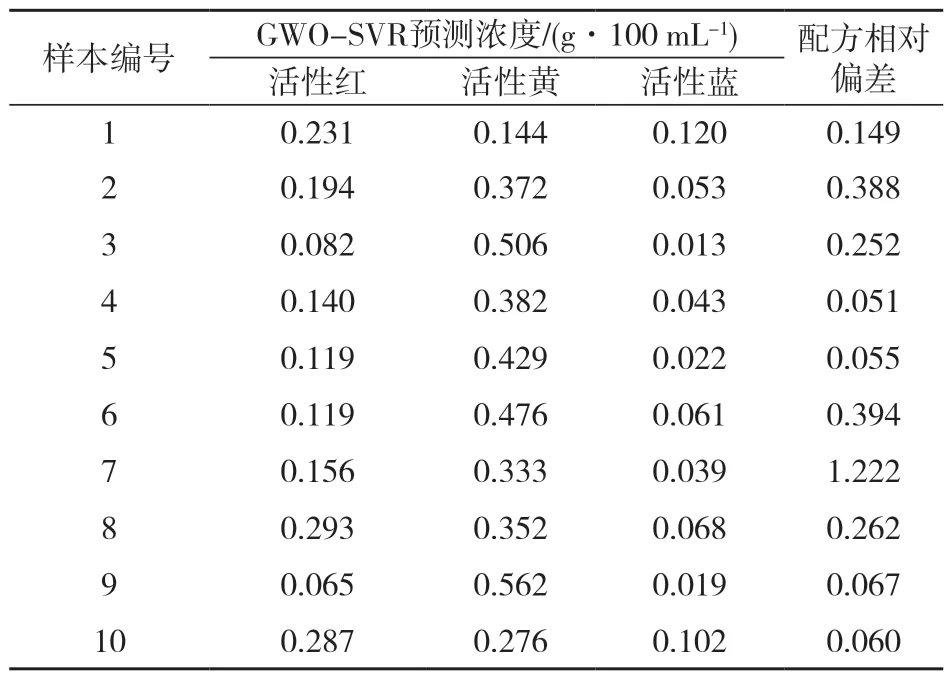
表5 GWO-SVR配色模型的预测结果Tab.5 Prediction results of GWO-SVR color matching model

表6 IGWO-SVR配色模型的预测结果Tab.6 Prediction results of IGWO-SVR color matching model
根据SVR、GWO-SVR、IGWO-SVR的配方预测结果,绘制三种模型的配方相对偏差曲线图,如图7所示。此外,计算三种模型预测结果的平均配方相对偏差,如表7所示。由曲线和平均配方的相对偏差可以看出,相较于前两种模型,IGWO-SVR的预测精度更高,评价偏差只有0.177,明显低于GWO-SVR和SVR模型。测试样本最大偏差0.418,最小偏差为0.070,误差波动更小,预测稳定性更强,证明了IGWO对SVR优化的有效性。
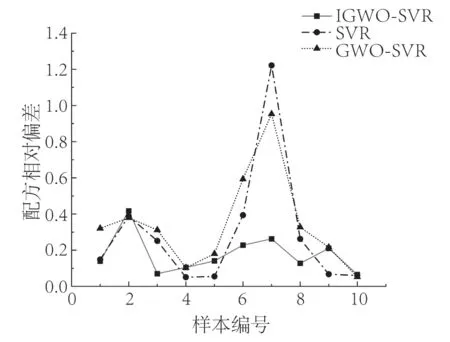
图7 SVR、GWO-SVR、IGWO-SVR配方相对偏差曲线对比Fig.7 Comparison of relative deviation curves of SVR, GWOSVR and IGWO-SVR formulations

表7 三种配色模型的平均配方相对偏差Tab.7 Average formula relative deviation of three color matching models
同时,为了说明此模型在配方预测中的适用性,本研究将其与BP神经网络、RBF神经网络、遗传算法(GA)优化SVR(GA-SVR)模型、粒子群算法(PSO)优化的SVR模型(PSO-SVR)的配方预测结果进行了对比。其中,GA算法将种群规模设置为10,最大进化代数为100,变异率和交叉率分别设置为0.1和0.3;PSO算法将粒子数设置为20,粒子加速因子设置为C1=2,C2=0,惯性常数设置为0.4;得到的所有预测配方相对偏差曲线如图8所示,其平均配方相对偏差如表8所示。由曲线图和平均配方模型可知,IGWO-SVR达到了理想效果。

图8 四种模型配方平均偏差曲线Fig.8 Average deviation curve of four model formulations

表8 各种配色模型的平均配方相对偏差Tab.8 Average formula relative deviation of various color matching models
4 结论
本文通过改进灰狼算法对支持向量回归(SVR)进行优化,得到染料配方预测模型,将SVR参数带入灰狼算法进行寻优,为避免陷入局部最优的情况,改进了位置更新策略和引入了非线性因子,得到的配方相对偏差为0.177,配色效果得到提高。与其他算法相比,更接近真实配方,表明IGWO-SVR在配方预测上的优越性。
与其他神经网络等模型不同,SVR对于数据集较小的情况有很强的适应性,属于小样本学习方法。本研究减小了数据集大小对模型的影响,使其能够适应实际生产需要,对于扩大人工速生材的应用具有重要意义。未来,可加入自定义初始化灰狼位置,或增加数据集,对其他优化算法进行深入探索。
