媒体报道诱导的离散传染病切换系统建模与分析
2023-08-05覃文杰张嘉敏向中义
覃文杰,张嘉敏,向中义
(1. 三峡大学 理学院, 湖北 宜昌 443002; 2. 云南民族大学 数学与计算机科学学院, 云南 昆明 650504;3. 湖北民族大学 数学与统计学院, 湖北 恩施 445000)
0 引言
传染病危害着人类生命健康、影响着社会经济发展,因此人们一直以来都在与传染病作斗争。通过发展传染病动力学模型来研究疾病的传播机制[1],可为传染病的预防和控制提供理论和数据支持,具有重要的现实意义。
影响传染病传播的因素有很多,近年来人们越来越关注媒体报道对人们行为方式的改变。在疾病暴发初期,媒体会通过网络、电视、报纸等不同的渠道实时报道相关情况,人们便会自觉采取相应的预防措施来阻止和减少疾病的传播,如出门戴口罩、少聚集、常消毒等[2]。因此国内外学者也持续关注媒体报道对疾病传播的影响。
2003年,RUAN等[3]用f(I)=k/(1+aI2)刻画媒体影响,得出基本再生数R0对疾病的暴发或消除起决定性作用。2007年,LIU等[4]通过构造传染率βexp(a1E-a2I-a3H)来研究媒体或心理效应对传染病的影响。2008年,CUI等[5]考虑含有媒体影响因子m的传染率βexp(-mI),建立SEI模型来讨论媒体报道对疾病传播的影响。2013年,刘玉英等[6]构造具有饱和性的媒体影响因子函数来刻画媒体对传染病感染率的影响。其他有关媒体效应的传染病模型可见文献[7-13]。
然而,目前基于媒体影响的传染病模型主要集中在连续模型,对于媒体影响的离散传染病模型还并不多见。事实上,对于某些传播速度较慢或疾病数据收集单位不连续的情形,用离散模型来刻画传播规律将更为合理。本文正是基于此而建立媒体报道诱导的离散传染病切换模型,研究媒体报道因子对传染病传播的影响。
1 模型的建立
在KERMACK和MCKENDRICK[14]的SIR仓室模型基础上,考虑具有媒体报道影响的SIR连续模型:
(1)
式中:S=S(t)、I=I(t)、R=R(t)分别表示t时间内易感者、感染者、恢复者的数量,b是内禀增长率,K是环境容纳量,d是自然死亡率,α是因病死亡率,γ是感染者的自然恢复率,β(I)表示疾病在媒体报道影响下的传染率。基于文献[3-6],考虑媒体影响因子m,以及疾病达到暴发点时感染者数量的临界值Ic,将其构造为非线性饱和函数:
这里所有参数都是非负数。
借助Euler离散[15-17],将模型(1)离散化,得到
(2)
由于模型(2)的前两个方程不含Rn,故简化模型(2)可得
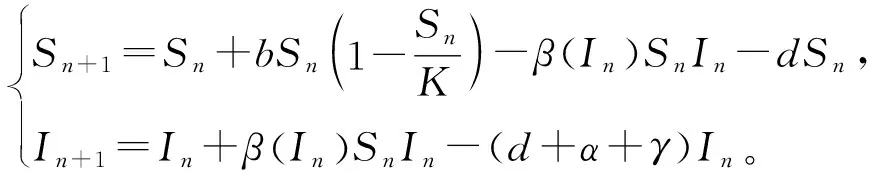
(3)
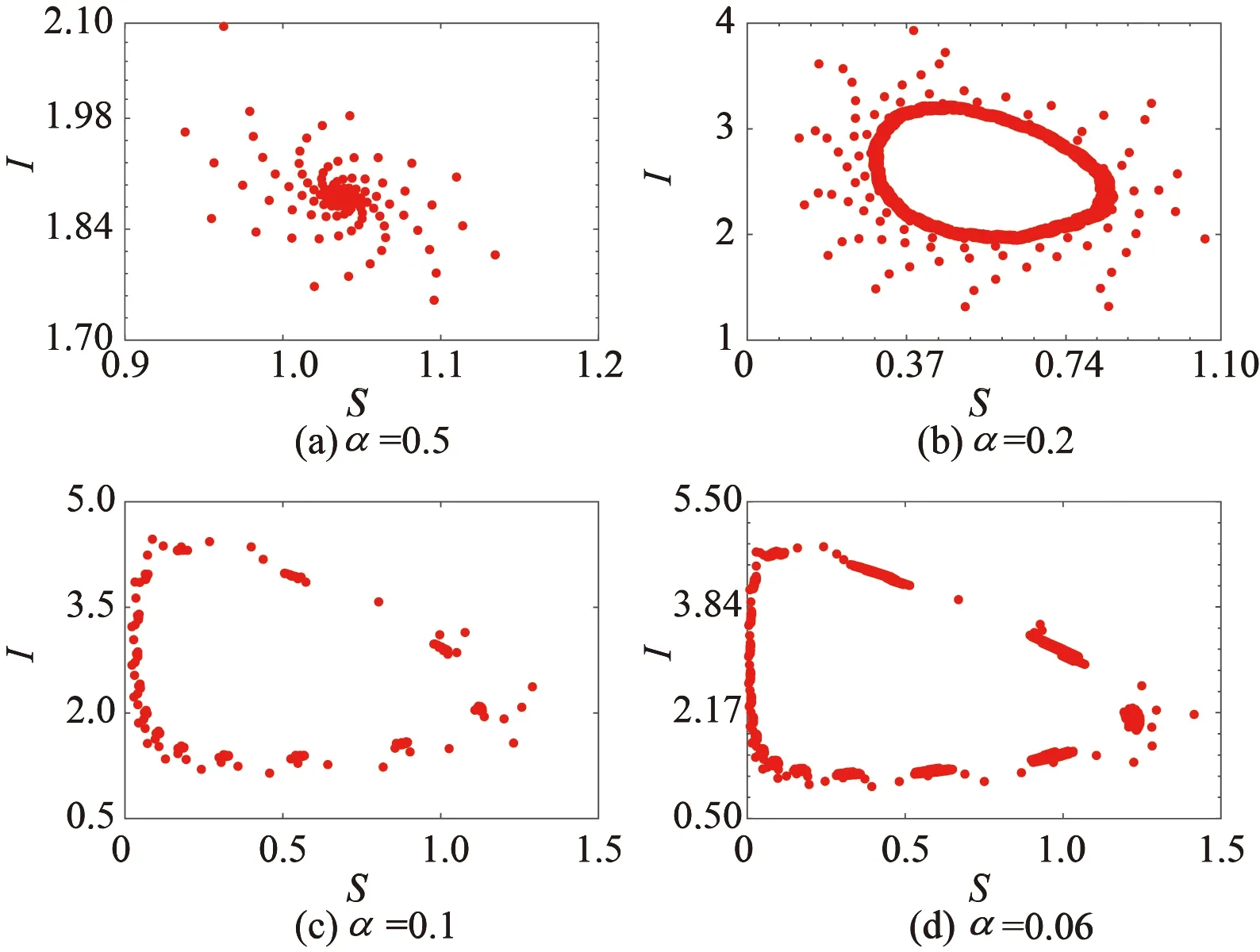
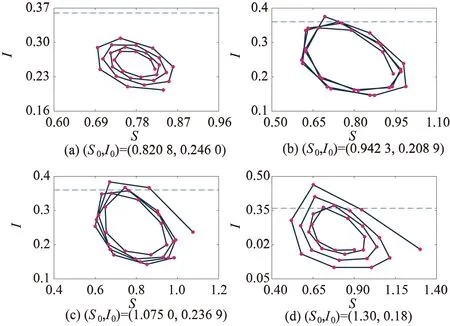
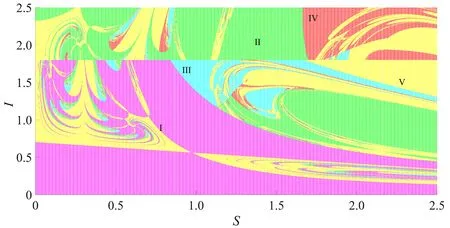
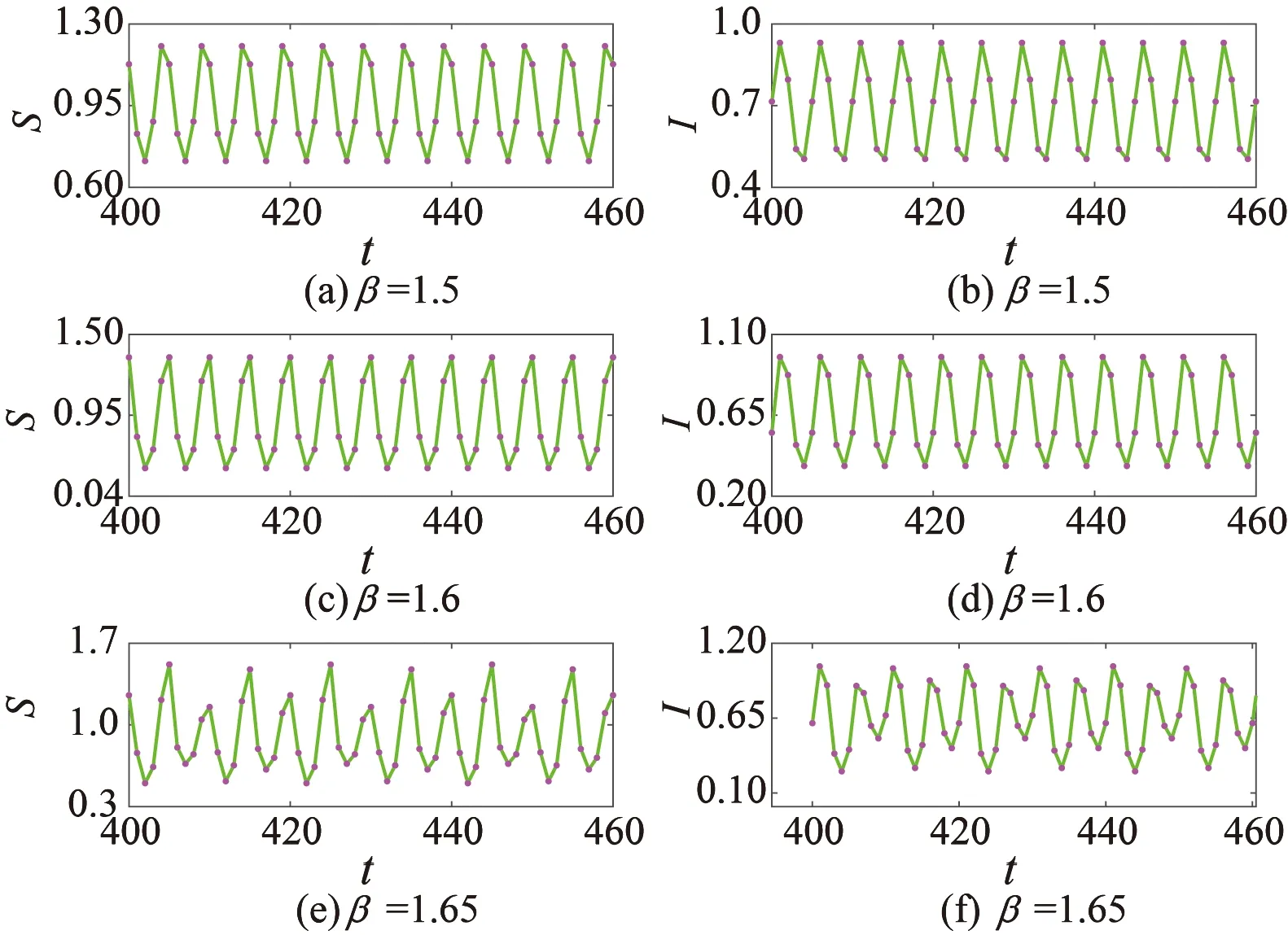
通常情形下,当感染人数较少(I (4) 然而随着感染人数的不断增加并达到阈值Ic时,相关媒体会持续关注此类传染病的传播与流行,全媒体的宣传和报道会使公众关注疾病的动态,从而采取相应的防护措施,改变个人行为,此时模型(4)为 (5) 综合模型(4)和(5),得到如下切换模型: (6) 式中: 离散模型(6)是一个基于阈值控制策略的动态切换系统,接下来将从理论和数值两方面来研究模型(6)的动力学行为。 为了叙述方便,将模型(6)改写成向量形式 (7) 式中: I(Z)=In-Ic,Z=[Sn,In]T。 特别地,切换系统定义在区域G1和G2的子系统分别记为FG1和FG2,下面将分析研究两个子系统正平衡点的存在性和稳定性。 子系统FG1的平衡点由如下方程决定: R0为子系统FG1的基本再生数,且有b-d>0。记D=b-d,M=d+α+γ。 定理1 若子系统FG1满足下列条件之一: (8) (9) (10) 由式(10)可得 子系统FG2的平衡点满足 (11) AI2+BI+C=0, (12) 式中: 方程(12)的判别式为 在R0>0的基础上对其进行分析: (1)当Δ=B2-4AC<0时,方程(12)不存在实根; (2)当Δ=B2-4AC>0,即 时,考虑以下3种情况: ①若C=1-R0<0,则方程(12)必存在一个正实根; ②若C=1-R0=0,则当-B/(2A)>0时方程(12)存在唯一的正实根,当-B/(2A)≤0时不存在正实根; ③若C=1-R0>0,则当-B/(2A)>0时方程(12)存在两个正实根,当-B/(2A)<0时不存在正实根。 定理2 若子系统FG2满足如下条件: (13) (14) 子系统FG2的雅可比矩阵为 (15) 显然,其特征方程为 P(λ)=λ2-tr(J2)λ+det(J2), (16) 式中: 由于离散切换系统各类平衡态存在的类型比较复杂,从理论上研究系统的动力学行为存在很多困难,因此本节将通过数值仿真方法研究传染病切换系统的复杂动力学行为,其中包括平衡点分支、单参数分支、初值敏感性和多吸引子共存等。 为了研究方便,给出切换系统真假平衡态的定义[19-22]: 为了研究系统以内禀增长率b和阈值Ic为分支参数的平衡点分支,固定参数K=0.5,β=1.8,m=0.28,d=0.02,α=0.35,γ=0.1,如图1所示,当b∈[0.65,2.50],Ic∈[0.1,1.5]时,离散切换系统存在6种情形的平衡态: 图1 系统以b和Ic为分支参数的平衡态分支图Fig. 1 Equilibria’ bifurcation diagram of system for parameters b and Ic 研究结果表明:通过媒体报道策略影响传染病的传播,要将离散切换系统的最终状态控制进入区域II-4,即两个子系统都不存在真平衡态,换言之,突发传染疾病不会成为地方病,不会影响到人们的正常生产、生活。一定要避免区域II-1及区域II-3所示的情形发生,因为传染疾病一旦形成地方病,将直接威胁着人们的身体健康、经济的发展、社会的稳定。 为了进一步研究切换系统的敏感参数、关键参数对系统动力学行为的影响,本小节将分别以自然恢复率γ、传染率β以及因病死亡率α为分支参数进行系统的单参数分支分析。 首先,固定参数b=2.8,K=1.8,β=0.52,m=0.8,d=0.08,α=0.25,Ic=1,以自然恢复率γ作为分支参数来研究切换系统的动力学行为,如图2所示。随着γ从0.05到0.40的不断变化,切换系统经历了周期解分支、倍周期解分支、混沌、周期减半、周期窗口、拟周期解等复杂的动力学行为,这也表明了突发性传染的自然恢复率在控制传染病传播方面起着相当重要的作用,在制定相关防控策略时一定要重点关注疾病的自然恢复率。 图2 系统以γ为分支参数的分支图Fig. 2 Bifurcation diagram of system for parameter γ 其次,固定参数b=1.8,K=3,m=0.02,d=0.3,α=0.3,γ=0.02,Ic=5,以疾病的传染率β作为分支参数来研究切换系统的动力学行为,如图3所示。当β∈[0.60,0.88]不断变化时,切换系统呈现出稳定解、混沌解、周期倍增解、多重稳定解等复杂的动力学行为。这说明了传染率对疾病的传播有着重要影响,为了控制疾病传播稳定在可控的范围内,需要采取措施降低传染率,如增大媒体宣传报道的力度就是间接降低疾病传染率的有效途径之一,这也是本文重点研究的内容之一。 图3 系统以β为分支参数的分支图Fig. 3 Bifurcation diagram of system for parameter β 接下来,研究因病死亡率α对系统动力学行为的影响,以α作为分支参数来研究切换系统的动力学行为。固定b=1.8,K=2.8,β=0.56,d=0.08,m=0.02,γ=0.001,Ic=2,如图4所示,随着因病死亡率α的不断变化,切换系统本身的动力学行为发生了不同的变化状态。 图4 系统以α为分支参数的分支图Fig. 4 Bifurcation diagram of system for parameter α 在图4 (a)(α=0.5)中,系统具有稳定解;当α从0.5减小到0.2时,系统出现一个周期解,如图4 (b)所示;当α继续变小达到0.1或0.06时,系统会出现混沌解,如图4 (c)和图4 (d)所示。 除了重要参数、敏感参数对疾病传播有着重要影响外,一定区域内易感者和感染者的初始密度对疾病的暴发状态也会产生不同的影响,本小节将系统研究切换系统在不同初值下的动态行为。 固定参数b=1.6,K=2,β=1.85,m=0.2,d=0.5,α=0.85,γ=0.09,Ic=0.36来研究初值对离散切换系统动力学行为的影响,如图5所示。 图5 系统的初始密度对疾病控制的影响Fig. 5 The impact of initial densities of system on disease control 图5中所示情形的初值都在切换线以下,即系统的感染者并未达到疾病暴发的阈值。具体而言,图5 (a)表示在初值(0.820 8,0.246 0)下,切换系统感染者密度未达到疾病暴发的阈值;图5 (b)表示在初值(0.942 3,0.208 9)下,切换系统感染者密度仅仅一次达到了疾病暴发的阈值,即突发性传染疾病只暴发一次;图5 (c)表示在初值(1.075 0,0.236 9)下,切换系统感染者密度两次达到了疾病暴发的阈值,即突发性传染疾病暴发两次;图5 (d)表示在初值(1.30, 0.18)下,切换系统感染者的密度多次达到了疾病暴发的阈值,即突发性传染疾病多次暴发。研究表明,为了抑制疾病的暴发流行,应该适当控制易感者和感染者的初始数量,让系统稳定在子系统FG1中,即图5 (a)、图5 (b)的情形。同时,为了控制疾病暴发,需要反复多次地对公众通过媒体宣传疾病传播的相关知识,使得人们对疾病防护引起相当的重视,从而改变人们的个人行为方式,达到控制疾病传播的目的。 为了更进一步研究离散切换系统的初始密度对突发性传染疾病传播的影响,下面给出了系统的盆吸引区域图,即选取参数b=0.8,K=3,β=1.85,m=0.57,d=0.5,α=0.85,γ=0.2,Ic=1.8,给出系统在区域S0∈[0,2.5],I0∈[0,2.5]的平面分支图,将5个区域分别记为I、II、III、IV及V,如图6所示。其中区域I表示疾病不会暴发为地方病;区域II表示疾病暴发一次后就不再流行;区域III表示疾病暴发二次就不再流行;区域IV表示疾病暴发三次就不再流行;区域V表示疾病会多次暴发流行。 图6 系统的盆吸引域Fig. 6 Basin of attractions of system 研究表明,当感染者数量超过疾病暴发的阈值时,要加大媒体的宣传力度、报道范围以及报道频率,使得公众提高警惕并养成良好的预防习惯,从而使得疾病即使在暴发多次后也要稳定于安全可控的范围之内。这也说明感染者和易感者的初始密度对后续疾病的流行趋势和程度会产生重要的影响。 因此,为了更有效地控制疾病传播流行,需要对易感者和感染者的密度进行实时监控和上报。 由3.3节相关内容可知,不同的初值会导致系统发生复杂多变的动力学行为以及致使系统稳定在不同的吸引子上,这就是吸引子共存现象,本节将关注系统多吸引子共存的研究。 切换系统的吸引子同样具有很强的初值敏感性,为了研究不同初始密度对共存吸引子的影响,在不同的初值状态下选取参数b=2.8,K=1.8,β=1.2,m=0.5,d=0.08,α=0.25,γ=0.46,Ic=3,如图7所示。图7 (a)为切换系统周期解情形,图7 (b)为系统拟周期解情形。很显然,随着时间序列的增大,图7 (b)所示情形必将导致系统呈混沌状态,这必然会给疾病防控带来一系列挑战。 图7 系统不同初值情形下的多吸引子共存Fig. 7 Coexisting attractors of system with different initial values 进一步,继续研究重要参数—疾病传染率β对系统多吸引子的影响,在初值(S0,I0)=(2,0.1)的情形下,固定参数b=3,K=2,m=0.1,d=0.5,a=0.85,γ=0.04,Ic=1.8,通过参数β的不断变化,切换系统呈现出不同的振幅和频率的吸引子。随着参加β不断增大,切换系统吸引子波动范围也不断变大,如图8 (a)—(f)所示。研究表明,疾病传染率在传染病传播中起着重要作用,防控部门可以通过媒体的宣传和报道降低疾病传染率,以达到有效控制传染病传播流行的目的。 图8 不同参数b下系统的吸引子Fig. 8 The attractors of system with different parameters β 考虑媒体报道对人们行为改变的切换效应,建立了一类由媒体效应诱导的离散传染病切换模型。一方面,从理论上研究了模型两个子系统的动力学行为,包括无病平衡点、地方病平衡点的存在性以及地方病平衡点的局部稳定性。另一方面,通过数值方法研究了敏感参数对系统动力学行为的影响。研究发现:关键参数的小扰动直接影响着疾病的暴发次数与频率,同时媒体报道可以降低疾病传染率,有效遏制疾病的流行与暴发。 事实上,决定系统切换的阈值相当关键,就目前掌握的文献,还没有对如何确定这个阈值进行相关的研究,这也是一个非常具有挑战的问题。同时结合具体的突发性传染疾病实例(如新型冠状病毒感染),在媒体效应的基础上考虑阈值对疫情防控的影响,将具有重要的理论和现实意义,这将是后续需要研究的重要课题。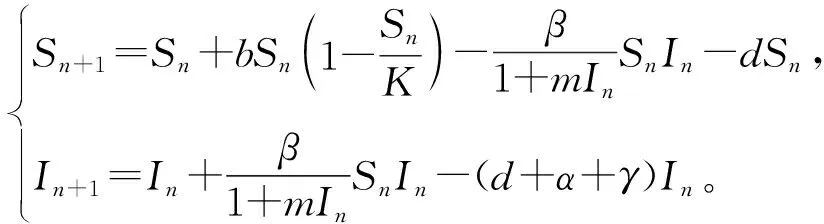
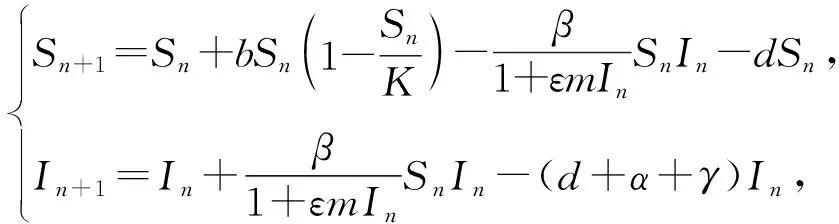
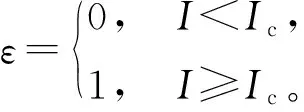
2 子系统的动力学行为
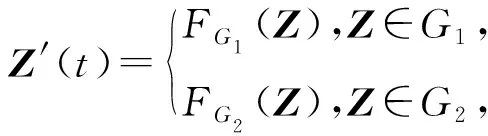
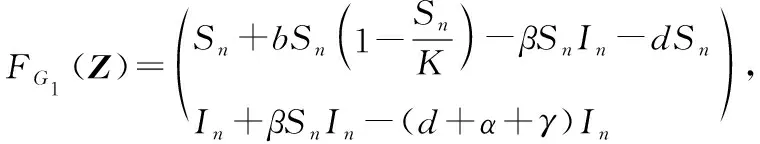
2.1 子系统FG1的动力学行为
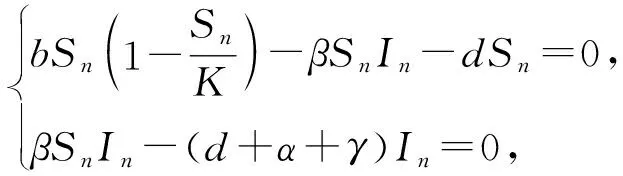
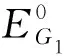
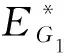
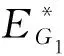
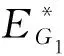
2.2 子系统FG2的动力学行为
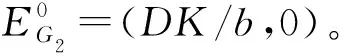
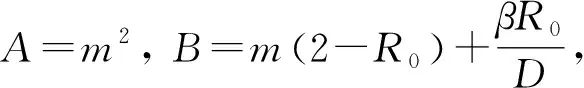
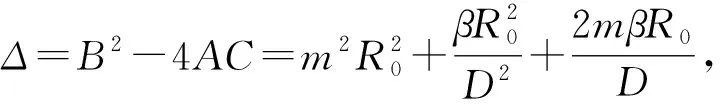



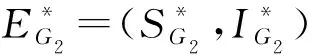
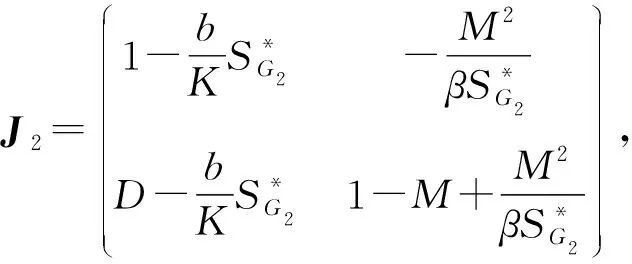
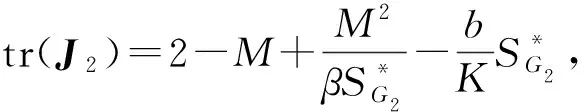

3 切换系统的复杂动力学行为
3.1 切换系统的平衡点分支分析
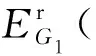

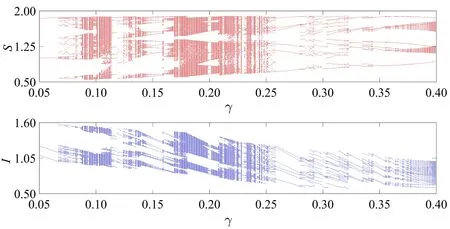
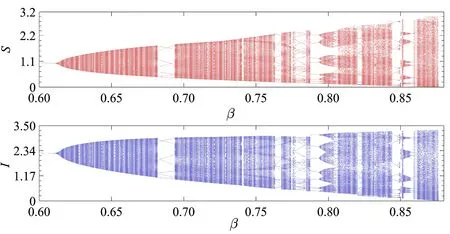
3.2 单参数分支分析
3.3 初值敏感性分析
3.4 多吸引子共存分析

4 结语
