基于Pearson相关性的雷达交叠信号识别

张先洪，李永祯

（1.国防科技大学电子科学学院CEMEE国家重点实验室，湖南长沙 410073；2.桂林长海发展有限责任公司，广西桂林 541001）

0 引 言

随着战场通信、雷达等电子设备的广泛应用,信号脉冲流愈加密集，信号分选环节的作用愈加关键［1］。信号分选指从交错的多部雷达信号中分离出每一部雷达信号的处理过程，也称雷达信号去交错处理。包括通过系统前端与硬件逻辑电路实现的预分选和利用计算机软件编程运算实现的主分选。目前，除了PDW 滤波器组、常规频率去交错器、捷变频去交错器等硬件方法外，主分选算法主要是基于脉冲宽度、脉冲到达方向、脉冲载频等参数利用扩展关联法、差直方图（CDIF）法、序列差直方图（SDIF）法、PRI变换法和TOA折叠分选方法等进行分选［2-9］。

然而，雷达对抗侦察接收机可能同时接收到多个雷达信号。同时在频域出现交叠的信号难以通过分选算法进行剔除，在低信噪比下，交叠和噪声都会导致信号的某些特征变得混乱，从而造成识别困难。

1 信号交叠对雷达辐射源信号识别的影响

信号交叠造成了侦察接收机单位时间内接收包数量的增加，同时会破坏了信号脉冲载波间原有的平衡关系。交叠部分的信号脉冲载波能量较多，对应的信号脉冲载波的幅度值较大。而非交叠区域的信号脉冲载波能量较少，对应的信号脉冲载波的幅度值较小。同时，交叠区域的信号脉冲载波和非交叠区域信号脉冲载波的波形与幅度值会有明显差异，因此在这种情况下交叠区域的信号脉冲载波与非交叠区域的信号脉冲载波之间的相关性较低，最终会导致所有信号脉冲载波间的相关性下降。

由于雷达对抗侦察接收机接收信号的过程实际上也是采样的过程，单位时间内接收包数量增多不可避免地导致了针对某一辐射源有效信号采样率的降低。而由奈奎斯特采样定理可知，当采样频率小于被采样信号频谱最高频率的两倍时，恢复的信号频谱易混叠失真，进而影响识别。

目前，对于一个相干处理周期的信号，大多采用信号脉冲载波融合的方式进行雷达信号识别。即通过相干处理周期内的信号脉冲载波的平均值或者相邻数个信号脉冲载波的平均值来代替所有信号脉冲载波的数据及特征内容。这些方法极大的依赖信号脉冲载波间的强相关性才能实现较好的性能。在无信号交叠的情况下，不同信号脉冲载波间的相关性较强，使用所有信号脉冲载波的平均值可以很好地替代其他信号脉冲载波的特征。而当信号交叠存在时，不同信号脉冲载波间的相关性较差，不同信号脉冲载波的差异较大，使用某一个信号脉冲载波特征来代替一个与其相差较大的信号脉冲载波的特征显然是不合适的，因此使用所有信号脉冲载波的平均值来代表与其差距较大的信号脉冲载波非常不合理。在这种处理下，融合的信号脉冲载波不能很好地反映辐射源特性对于不同信号脉冲载波的影响，这最终会导致识别性能的显著降低。

在不同的信号交叠环境中，由于雷达辐射源发射功率的变化以及信号脉冲载波交叠情况的差异，侦收信号幅度值是随之波动的。而大多数雷达辐射源信号识别系统都是需要提取幅度特征，幅度值的改变直接影响了这些系统提取的特征，进而影响到这些系统的识别性能。

2 基于Pearson算法的抗交叠雷达信号识别系统

如图1 所示，基于Pearson 算法的抗交叠雷达信号识别系统主要包含4 个模块:信号交叠的判断、动态的数据预处理、特征提取和信号分类模块。信号交叠的存在和信号交叠的改变首先在第一模块被判断出来。随后，根据信号交叠的判定结果，不同的信号脉冲载波处理策略被应用在第二模块。具体地，在无信号交叠的环境中，数据维度被通用信号脉冲载波融合算法快速降低。而在信号交叠恒定的情况下，基于Pearson 相关性计算的信号脉冲载波筛选算法被应用来提升正确识别率。随后，在第三模块提取信号特征。最终，在第四模块信号样本被分类器有效分类。

2.1 信号交叠检测

考虑到雷达辐射源要正常发挥作用，必须发射一定相干处理周期的连续脉冲，在该周期内信号脉冲载波固定、速率稳定的情形，信号脉冲载波的相关性变化较慢。因此，文章主要考虑该条件下的交叠检测。在该情形下，信号脉冲载波相关性较易度量。由于信号脉冲载波相关性变化较慢，滑动窗口的局部特征可以很好地表示所有样本的全局相关性特征。基于以上分析，基于Pearson 相关性的算法被提出来进行恒定信号交叠环境下信号脉冲载波的选择。

基于Pearson相关性计算的信号脉冲载波筛选算法使用滑动窗口的局部相关性来表示所有样本的全局相关性，以在有效度量信号脉冲载波相关性的同时保持较低的计算复杂度。

此外，为在不同的信号交叠环境中执行合适的信号脉冲载波处理方法，需要先确定信号交叠的存在和改变。

是否存在雷达信号交叠可以通过测量单位时间内指定辐射源有效脉冲数量进行判断。在无信号交叠的情况下，一个覆盖区域内信道被同一辐射源信号所独占。然而在信号交叠的环境中，侦察接收机可以感知到信道正在传输的指定辐射源有效脉冲数量的减少。因此，通过记录单位时间内指定辐射源接收包数量，信号交叠现象能够被有效检测出。

2.2 基于Pearson相关性计算的脉冲信号筛选

与脉冲信号融合算法相比，脉冲信号筛选方法会更加有效且对信号交叠鲁棒。具体地，通过选择几个弱相关的单独脉冲信号来表示所有脉冲信号的特性，可以在降低数据维度的同时将特征保持在最大水平。这是因为相同数量的强相关脉冲信号相比于相同数量的弱相关脉冲信号所包含的总信息较少。根据信息论，联合熵可以直接来表示由两个事件组合而成的总信息量。特别地，两个脉冲信号序列的联合熵可以表示为

式中，q，w是不同的脉冲信号序列，E(q)和E(w)分别是脉冲信号序列q和w的熵，E(q,w)表示脉冲信号序列q和脉冲信号序列w的联合熵。互信息ψ(q;w)与Pearson 的相关系数rq,w正相关。由于对于给定的脉冲信号序列q和w，E（q）和E（w）不变，所以两个脉冲信号q，w之间的相关性越强，互信息ψ(q;w)越大，所包含的信息E(q;w)就会越少。

基于以上分析，脉冲信号筛选算法的核心是选择几个弱相关的脉冲信号，而不是对其进行简单积累或平均。通过使用被选择的弱相关脉冲信号的特征来表征所有脉冲信号的特性，数据维度可以被有效降低，同时信息量也尽可能保留，从而可以实现对信号交叠鲁棒的效果。

本文使用Pearson方法来计算脉冲信号序列间的相关性。

Pearson 相关性系数使用两个序列分量（q和w）的协方差和标准差来定义脉冲信号相关性rq,w的强弱:

式中，l是序列q和序列w的长度，和分别是脉冲信号序列q和序列w的均值。具体地，在每个信号样本滑动窗口中，序列q和序列w分别代表该滑窗中第q个脉冲信号的幅度值序列和第w个脉冲信号的幅度值序列。因此，rq,w代表了对应滑动窗口中第q个脉冲信号序列和第w个脉冲信号序列间的Pearson 相关性系数值。基于Pearson 相关性计算的脉冲信号筛选算法的核心是选择几个弱相关的脉冲信号，同时不对它们进行融合处理。通过使用被选择的脉冲信号信息来替代所有脉冲信号的特征，数据维度能被显著减少的同时，伴随着较少的信息损失。

基于Pearson相关性计算的脉冲信号筛选算法主要包含3个步骤:

1）分别选择适合每个滑动窗口的识别脉冲信号。由于弱相关的脉冲信号组合所包含的总的特征信息较多，为了包含更多的特征信息，每个滑动窗口中具有最弱相关性的脉冲信号组合首先被确定。具体地，通过Pearson方法计算了第f个滑动窗口的内部相关性系数进而产生了该滑动窗口对应的相关性矩阵Rf。相关性矩阵Rf中的元素rq,w代表了脉冲信号序列q和脉冲信号序列w之间的序列相关性系数。随后，相关性矩阵Rf中的元素按照从小到大的顺序排列产生了一个新的数列If。选取数列If中最小相关性元素对应的两个脉冲信号(a和b)来组成脉冲信号组合Cf。在脉冲信号组合Cf达到设定的所需脉冲信号数量之前，脉冲信号将按照添加脉冲信号后被添加的脉冲信号和原有脉冲信号组合之间总的相关性最弱的原则被逐个添加到脉冲信号组合Cf中。类似地，对所有的滑动窗口执行相同的脉冲信号组合的确定操作。因此每个滑动窗口所选择的脉冲信号组合就被确定了。

2）将所有滑动窗口的脉冲信号组合进行有效的统计进而确定适合所有滑窗样本的脉冲信号组合。根据少数服从多数的原则，在所有滑动窗口中最常出现的脉冲信号组合（众数组合Ctmp）被选择作为步骤2的输出。在这种情况下，所有样本的全局相关性特点被滑动窗口的局部相关性特征所表示。

3）从步骤2）输出的脉冲信号组合中筛选出符合频率空间约束的脉冲信号组合作为最终用于辐射源识别的脉冲信号组合。由于两个脉冲信号序列号差距越大它们的频率差距也越大，这就会造成由相同辐射源的两个脉冲信号的相位改变有着更显著的差异。为了同时兼顾脉冲信号相位改变不同的影响以及脉冲信号相关性的影响，脉冲信号的频率空间约束被添加到本文算法中。具体地，在最终脉冲信号组合Cs中的脉冲信号应该从以下3 个脉冲信号区间中的每一个区间均进行选取，分别是区间［0，10)，［10，20)，以及［20，30］。如果步骤2）输出的脉冲信号组合Ctmp不满足这一条件，那么在所有滑动窗口中出现次数排名第二的脉冲信号组合将会被选择作为步骤2）的输出。以此类推，如果出现次数排名第二的脉冲信号组合不满足频率空间约束，那么出现次数排名第三的脉冲信号组合将会被选择作为步骤2）的输出。

3 实验结果分析

3.1 数据集构建与评估指标

本文通过仿真实验产生21个类别的雷达辐射源信号，每部雷达分别产生1 500个单脉冲数据，脉宽为3.5 μs，信噪比为20 dB，采样频率为100 MHz，中频频率为18 MHz，中频带宽为5 MHz，信号之间在上升沿和下降沿的宽度设置上有微小差异。根据单脉冲数据，设置5 组不同的脉冲重复周期（10 kHz、50 kHz、100 kHz），每个样本采集3个脉冲长度形成脉冲串，并按最长信号位数循环补齐，再用分选后不含交叠的脉冲串与同时交叠脉冲串相结合的方法构建包含交叠信号的雷达信号数据集，其中交叠信号即随机选择脉冲样本叠加输出，在数据集中随机两组交叠的形式输出的脉冲串样本占20%。

识别算法的评估指标为准确率，按照下式计算:

准确率是算法模型判断正确的数据占总数据的比例。其中，TP为将正类正确预测为正类的数量，TN为将负类正确预测为负类的数量，FP为将负类错误预测为正类的数量，FN为将正类错误预测为负类的数量。

3.2 网络参数

分类器采用ESN 网络拟合加分类的学习方法［10-11］，分别利用未经去交叠处理的雷达信号数据集和基于Pearson算法去交叠后的雷达信号数据集训练不同的网络以开展对比实验。

在分类方法中选用了KNN 与SVM，KNN 使用自动超参数优化，通过五重交叉验证的方式选取参数；SVM 采用“一对一”策略，并对输入变量进行标准化，正则系数通过五重交叉验证的方式进行选取。在所有实验中，每个模型都配置了相同的超参数。

3.3 实验结果

将未经去交叠处理的雷达信号数据集和基于Pearson 算法去交叠后的雷达信号数据集分别输入ESN网络进行学习拟合，部分训练和测试效果如图2所示。

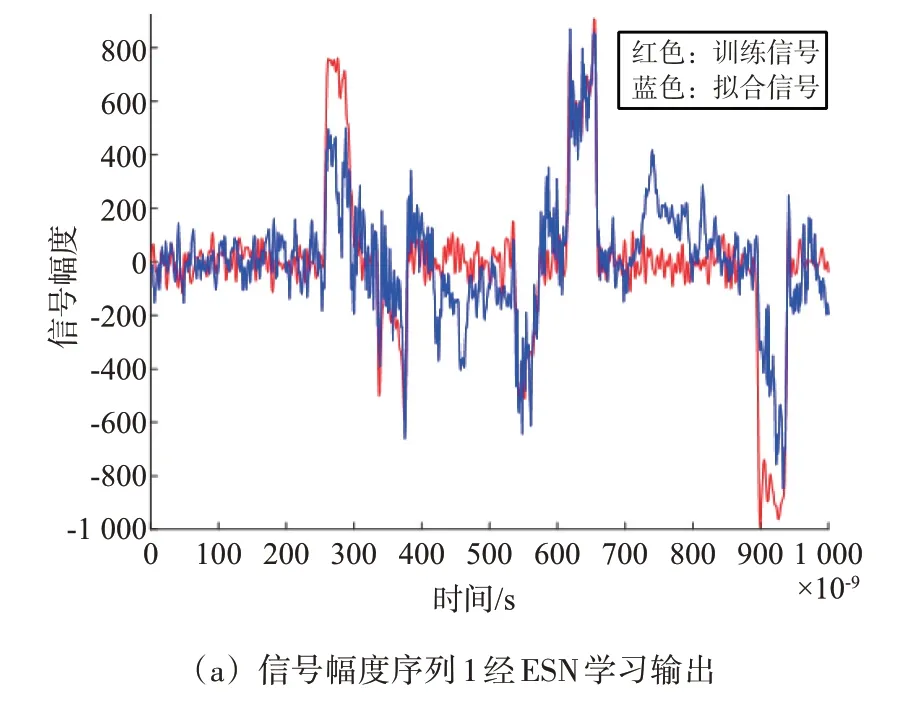
图2 部分时序信号经ESN学习输出

将学习到的ESN 输出表示作为分类算法的输入进行分类，经过蒙特卡洛实验统计后识别准确率结果如表1所示。

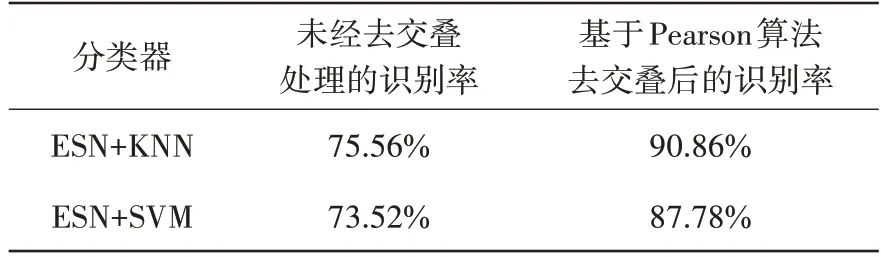
表1 实验分类精度

可以看出，未经去交叠处理的数据进行特征提取与识别后，识别准确率最高仅达到75.56%，其错误主要发生在交叠信号样本的识别测试中。经过本文的算法进行去交叠处理后，识别准确率最高达到了90.86%，验证了方法的可行性。

4 结束语

信号间脉冲相关性越弱，经选择时包含的总信息量就越大。因此，本文在接收机处理的信号脉冲数量一定时，利用基于Pearson 相关性计算的信号脉冲载波筛选算法尽可能地选择相关性较弱的信号脉冲，经筛选后的信号用于进行辐射源识别。在这种情况下所选择的信号脉冲包含的特征信息最多，因此系统能够最大程度适应信号交叠情形。实验结果表明，该信号脉冲筛选策略可以有效提高信号交叠情形下的识别率。