基于双重虚警控制XGBoost的海面小目标检测

施赛楠，姜 丽，李东宸，吴旭姿

（1.南京信息工程大学电子与信息工程学院，江苏南京 210044；2.中国船舶工业系统工程研究院，北京 100094；3.江苏开放大学信息工程学院，江苏南京 210036）

0 引 言

目前，海面小目标是海洋雷达探测的重点和难点对象，如小船、潜望镜、浮冰、蛙人、飞机残骸等［1-3］。这类小目标的弱回波被淹没在强杂波背景下，导致检测时信杂比（Signal-to-Clutter Ratio,SCR）很低，大大降低了检测概率。通常，需要采用长时累积技术，提高目标的信杂比。在秒级长时观测下，海杂波呈现出非平稳、非均匀的空时变性和重拖尾的强非高斯性，而小目标的幅度和多普勒偏移都不再保持恒定［4-5］。因此，海杂波和目标回波都难以建模为简单的参数化模型，这意味着很难发展基于杂波模型的最优或近最优检测方法。

在长时观测下，一种公认的有效途径是基于多维特征的检测方法，从不同域提取多个特征构建特征向量，进而将检测问题转换为分类问题。因此，该类方法的研究重点在于多域特征提取和特征空间中的分类器设计。在一维特征空间中，分类器简化为门限，研究主要在特征提取方面。典型的方法有基于分形的检测方法，提取Hurst 指数［6］、变换域的多尺度指数［7-8］、全维度特征［9］等。在三维特征空间中，发展了一系列以凸包学习算法为核心的单分类器，通过凸包的伸缩实现虚警控制。在文献［10］中，从时域和频域提取特征，构成了基于三特征的检测器，在高信杂比下性能显著提升。为了更加精细化描述频谱特性，文献［11］提出了基于时频三特征的检测器，适用于目标频偏落在主杂波带外。为了利用全极化维度信息，文献［12］提出了基于极化三特征的检测器，依赖于不同极化的信杂比高低。随后，为了进一步提升海面目标探测性能，联合更多的特征是必然趋势。但是，随着特征空间维数的增加，凸包学习算法的计算量极大甚至在高维中无法计算，亟需寻找新的高维分类器。

为此，有学者尝试引入机器学习中的两分类算法［13-16］，但这些算法适用于两类错误率均衡的情况。因此，在高维特征空间中，分类器设计的主要难点是实现虚警控制。目前，大致可以分为两类方法。第一类是通过搜索分类器的某个参数，达到给定虚警率。Guo 等人［13］将K 近邻（K Nearest Neighbors,KNN）算法引入到七维特征空间中，通过搜索邻近数目参数，实现虚警控制。Chen 等人［14］通过对一类支持向量机（One Class Support Vector Machine,OCSVM）中的超参数搜索，从而保证虚警率达到给定值。Shi 等人［15］提出基于随机森林（Random Forest,RF）的检测器，建立分裂因子与虚警率的函数关系，进而对给定虚警率下的参数设置具有一定指导。第二类是从分类器内部结构出发，打破原先两类错误率均衡的模式，达到虚警控制。Li等人［16］提出改进支持向量机（Supported Vector Machine,SVM）的检测器，通过改变目标函数中的两类惩罚参数，不断迭代更新获得与虚警率匹配的参数。这是一种从结构层面的思路，具有很好的借鉴意义。但是，上述分类器都需要不断地搜索参数，这意味着参数设置的精度与虚警率密切相关，因而存在虚警率控不准的问题。

针对高维特征空间中分类器虚警控制难的问题，本文提出一种基于双重虚警控制极限梯度提升（XGBoost）的海面小目标检测方法。检测方法的主要创新在于以下两个方面。在特征提取方面，提取了时域、频域、时频域中的7 个特征，构建高维特征空间。在分类器设计方面，提出改进的XGBoost 两分类器，实现对虚警率的精准控制。从结构层面，在原先XGBoost［17］中引入两类错误率的惩罚因子，实现第一重粗虚警控制。从参数层面，将分类概率值作为统计量，实现第二重精虚警控制。

1 高维特征空间中的两分类器设计

1.1 特征提取和互补性分析

假设雷达在检测单元（Cell Under Test,CUT）中接收到N个连续脉冲，即观测向量z=［z（1）,z（2）,…,z（N）］T。由于雷达目标检测就是判断观测向量是否有目标，则检测问题描述为以下的二元假设检验［9-12］:

式中，c表示海杂波向量，s表示含目标回波向量，zp表示CUT 周围第p个参考单元的回波向量，P表示参考单元的总数目。H0假设表示CUT 中纯海杂波，H1假设表示CUT中含有目标回波。

事实上，不同的特征反映了海杂波和含目标回波在不同方面上的差异性，比如能量、物理散射方式、几何形状等方面。在时域中，提取Hurst 指数（Hurst Exponent,HE）［6］和相对平均幅度（Relative Average Amplitude,RAA）［10］，分别反映了幅度的分形特性和能量特性，记为ξ1,ξ2。在频域，提取相对多普勒峰高（Relative Doppler Peak Height,RDPH）和相对向量熵（Relative Vector Entropy,RVE）［10］，记为ξ3,ξ4，前者衡量了海杂波和目标带宽大小的差异性，后者描述了两者频谱在频域的混乱度。在时频域，提取脊能量（Ridge Intensity,RI）、连通区域数目（Number of Regions,NR）、最大连通区域尺寸（Maximum Size,MS）［11］，精细化描述了海杂波和目标频谱的几何动态特性，记为ξ5,ξ6,ξ7。

下面，使用IPIX 数据集的10 组数据［18］测试特征在不同探测环境下的检测性能。实验中，观测时间为0.512 s，虚警率为10-3。图1 给出了7 个特征在HH 极化下的检测结果。可以发现，2 个时域特征、2 个频域特征和3 个时频域特征在不同数据上的检测概率明显存在波动性，没有哪个特征具有最优检测特性。这表明这7 个特征在检测能力方面具有互补性，联合使用可以进一步提升性能。

图1 7个特征的互补性分析

1.2 两分类器的虚警控制

为了精细化挖掘海杂波和含目标回波的差异性，将时域、频域、时频域提取的7 个特征联合，构建高维特征空间。因此，CUT 的观测向量被压缩为一个七维（7D）特征向量:

至此，式中的检测问题转换为高维特征空间中的分类问题:

对于海洋雷达，一旦开机后可以采集大量的海杂波数据。但是由于感兴趣小目标的空间稀疏性和种类多样性，很难获得大量的含目标回波。因此，很多学者将式（3）变为高维特征空间中的单分类问题［1，10-12］，也称为异常检测。事实上，单分类器只用了海杂波的信息，缺少含目标回波的信息，存在冗余性。因而，两分类器将是提升性能的必然选择。在两分类器中，需要获得两类均衡的训练样本，才能保证较好的分类性能。考虑到含目标回波的数据稀缺性，一种可行的方法是仿真目标回波，具体参照文献［13,15］。

事实上，特征提取过程涉及较多非线性操作，因而无法对高维特征的统计特性进行显示函数表述。假设已知两种假设下的样本x∈R7条件概率密度函数（Probability Density Function,PDF），记为P(x|H0)和P(x|H1)，根据奈曼-皮尔逊（Neyman-Pearson,NP）准则，检测器的设计等价于寻找H1假设下的判决区域Ω:

式中，Pd为检测概率，Pfa为设定的虚警率。当样本落在判决区域Ω内，判决为H1假设；否则，判决为H0假设。目标函数以寻求高维特征空间中最优判决区域为目的，除非P(x|H0)和P(x|H1)解析表达式非常简单，否则式（4）很难获得解析表达式。虽然目标回波仿真可以获得两种假设下特征向量的大量样本，但P(x|H0)和P(x|H1)的表达式是无法获知的。因此，在高维特征空间中，如何从两种假设样本中训练获得具有虚警可控的判决区域是两分类器设计的难点和核心问题。

2 基于双重虚警控制XGBoost的检测器

2.1 高维特征域检测器结构

在特征提取过程中，不同的特征来自不同域，且反映了海杂波和含目标回波在不同方面的差异性。所以，当联合多个特征时，必须考虑特征尺度不同的问题，常规的方法是对每一维特征进行归一化预处理。在获得H0假设下的M个观测向量后，对每个观测向量提取7个特征，构成M个7D 的特征向量xi∈R7,i=1,2,…,M。然后，对式（2）中CUT特征向量进行归一化处理:

图2 是基于双重虚警控制XGBoost 检测器的流程图，包含检测分支和训练分支，前者实现在线检测而后者需要离线训练。在检测分支中，首先，对CUT 观测向量提取特征，将观测向量凝聚为式中的一个特征向量；其次，按照式对特征向量进行归一化处理，最终获得式中的归一化特征向量；然后，双重虚警控制XGBoost两分类器对输入的归一化特征向量输出概率预测值，作为最终的统计量。最后，判断统计量是否超过判决门限，完成判决。训练分支作为检测的辅助分支，主要为检测分支提供了XGBoost 两分类器的最优模型参数和判决门限。为了实现两分类器的正确分类，可按照文献［15］中的方法产生两类均衡的样本数据。假设H0和H1假设的样本各有M个，分别记作标签0 和1。因此，两类特征向量样本训练集Θ为

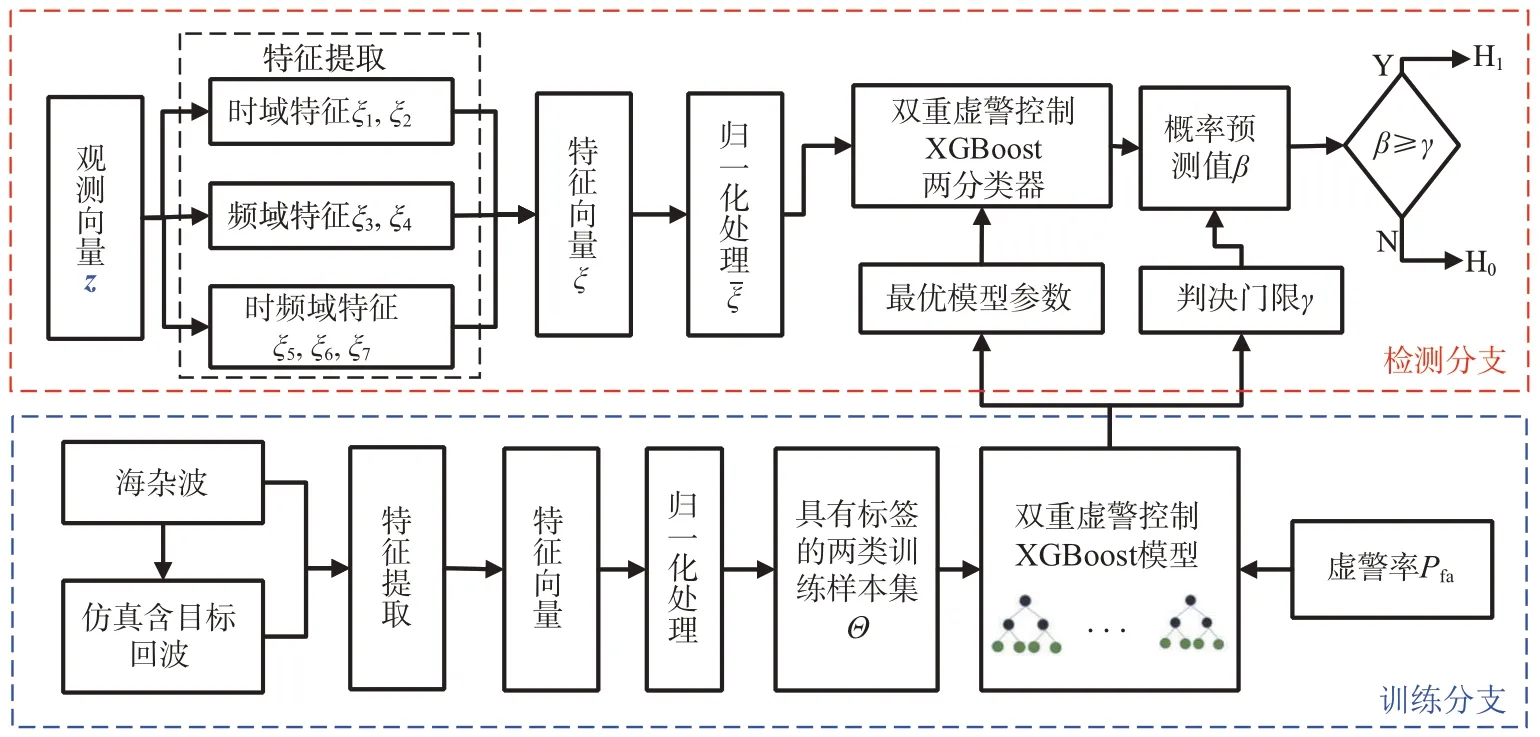
图2 基于双重虚警控制XGBoost的检测器流程图

用于训练学习双重虚警控制的XGBoost 模型的最优参数。

2.2 具有双重虚警控制的XGBoost两分类器

在两分类器中，通常存在两种错误率:H0假设误判成H1假设，H1假设误判成H0假设。在现有的SVM、KNN、决策树、随机森林、XGBoost 等机器学习［13，15-16］算法中，损失函数是以两类平均错误率为准则，与雷达目标检测中的NP 准则是不一致的。因此，在引入这些算法时，第一步必须解决虚警率控制的问题，这是雷达目标检测的基本要求和前提条件。

XGBoost 算法［17］将分类回归树（Classification And Regression Tree,CART）作为子模型，并级联K个子模型进行线性组合，最终达到准确分类。表1给出了具有双重虚警控制的XGBoost 两分类器的具体实现流程。

表1 具有双重虚警控制的XGBoost算法

在第一重中，通过不断调整惩罚因子，主要实现结构层面的粗虚警控制。首先，引入两类错误分类的惩罚和正确分类的惩罚，重新定义损失函数

式中，y,∈{0,1}分别为真实值和预测值，C（0|1）为真实值1判为0的惩罚，C（1|0）为真实值0判为1的惩罚，C（0|0）和C（1|1）为正确判断的惩罚。令C(0|0)=C(1|1)=0，C(0|1)=c1，C(1|0)=c2，式（8）简化为

式中，c1为出现漏检的惩罚，c2为出现虚警的惩罚，与虚警率相关。在固定c1的条件下，当增大c2时，H0假设下的样本一旦出现误判，则损失函数值增大，两分类器将朝着虚警率小的方向学习参数。当c1=c2时，分类器不再区别对待两类错误率，退化为原始的XGBoost两分类器［17］。

为了防止过拟合，第k棵CART 树的目标函数定义为

式中，fk-1(xi) 为输入样本xi的第k-1棵树的输出，J为叶子节点的个数，ωkj为第j个叶子节点的权重，α为复杂度惩罚项，λ为惩罚正则项。为了提高分类精度，式（10）进行泰勒二阶展开:

式中，gi=分别为损失函数的一阶、二阶偏导。从叶子节点出发，对所有叶子节点进行累积，式（11）进一步化简为

式中，Gj=∑i∈Ijgi和Hj=∑i∈Ijhi分别表示映射为叶子节点j所有输入样本的一阶、二阶导和。由此，可计算第j个叶子节点区域的最佳拟合值

将式（13）代入式（12）中，得到最小目标函数

这也称为打分函数，函数值越小，代表树结构越好。

接下来，如何选择不同的特征值进行分裂。假设每次左右子树分裂时，以最大程度减小目标函数的损失为准则。令GL，HL，GR，HR表示当前节点左右子树的一阶、二阶导数和，则定义分数增益函数为

遍历所有的分裂方式，最终选择以最大分数增益对应的特征进行分裂。

然后，更新预测值

式中，v∈[0,1]是学习率，用于控制过拟合度。

最后，更新迭代得到K个CART 树，最终输出值为

根据蒙特卡洛方法，将训练集Θ中属于H0假设的M个样本作为改进XGBoost两分类器的输入，获得最终的分类结果。那么，计算当前虚警率为

通常，当前虚警率PF和给定的虚警率Pfa是不一样的。为了获得给定的虚警率Pfa，在固定惩罚因子c1的条件下，不断更新惩罚因子c2，直到PF接近Pfa，最终获得XGBoost两分类器的最优参数。

由于第一重中需要对惩罚因子进行搜索，势必存在虚警率无法精准控制的问题。因此，设计了第二重的虚警控制。在第二重中，主要实现参数层面的精虚警控制。

首先，将第一重中获得的模型参数作为两分类器的最优模型参数。将训练集中属于H0假设的M个训练样本作为输入，获得M个预测为H1假设的概率值为

然后，对M个概率值按从大到小进行排序，记为{β1,β2,…,βM}，满足β1≥β2≥… ≥βM。

最后，根据蒙特卡洛方法，特定虚警率Pfa下的判决门限为

式中，［］表示取整数。

图3 演示了基于改进的XGBoost 两分类器的虚警控制过程，假设设定的虚警率Pfa为10-3，横轴表示40 组数据的序号。在第一重中，只有5 组数据的虚警率被控制在10-3，其余数据的虚警率在设定值附近上下波动，存在0.000 1左右的误差，这个误差与设置的误差值ε=0.000 1一致。当采用双重虚警控制时，两分类器的虚警率被精准控制在10-3，满足实际雷达的探测要求。

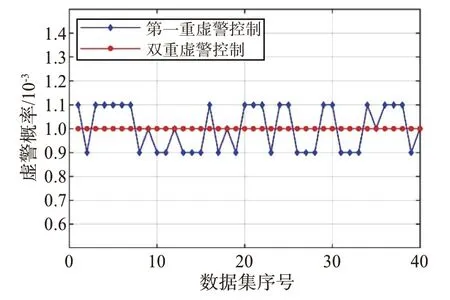
图3 实测数据下双重虚警控制演示

事实上，风速、风向和海况等海洋气象参数会对海洋雷达的检测性能产生影响。由于探测场景的改变，海杂波的统计特性会随之发生变化。如若仍用原先数据训练的模型进行检测，则检测性能存在一定的损失。因此，当探测场景发生改变时，必须动态更新当前环境下分类器的模型参数。首先，需要在线采集当前环境下的海杂波数据，获取相应的仿真回波数据。然后，使用新的两类数据离线训练当前环境下的模型参数，为在线检测提供虚警可控的检测器。所以，本文提出的检测器具有较好的鲁棒性，自适应于不同的探测场景，实现对海洋环境的恒虚警特性。

3 实验结果和性能评估

本文使用的实测数据来自IPIX 雷达公开的数据库［18］。X波段雷达工作在驻留模式下，脉冲重复频率为1 000 Hz，距离分辨率为30 m。实验目标是用铝丝包裹直径约1 m 的塑料小球，随海面上下漂浮。实验中使用了1993 年的10 组数据和1998 年数据的1组，各组数据均含有同步收集的HH、HV、VH和VV极化通道的数据［11,13,18］。

3.1 两分类器的参数设置

事实上，XGBoost 两分类器的参数大致分为学习参数和结构参数两大类。第一类为学习参数，比如CART 树的叶子节点权重、叶子节点个数等。这些参数高度依赖于训练数据，当探测环境发生变换时，需要不断地学习和更新。因此，在图2中，训练分支就是用于训练获取最优学习参数。第二类为结构参数，比如CART 树数目K、树最大深度D，学习率v、惩罚项等。建议设置学习率v=0.15，复杂度惩罚项α=0，惩罚正则项λ=1。然而，K和D直接决定了模型的结构，主要是这两个参数对检测性能产生较大影响，需要根据数据提前设置。

在二维特征空间中，图4 演示了参数K对XGBoost 分类器判决区域的影响。可观察到，当K不断增大时，分类器模型不断地迭代更新，判决区域也随之优化，表明海杂波与含目标回波样本能更好地被分类。虽然联合多个弱学习器能获得性能提升，但这种性能优势不是无止境的。当CART 树达到一定数量时，分类器性能提升不明显。此时，再增加CART 树，只能带来计算量的增加。因此，需要找到计算代价和性能之间的平衡点。

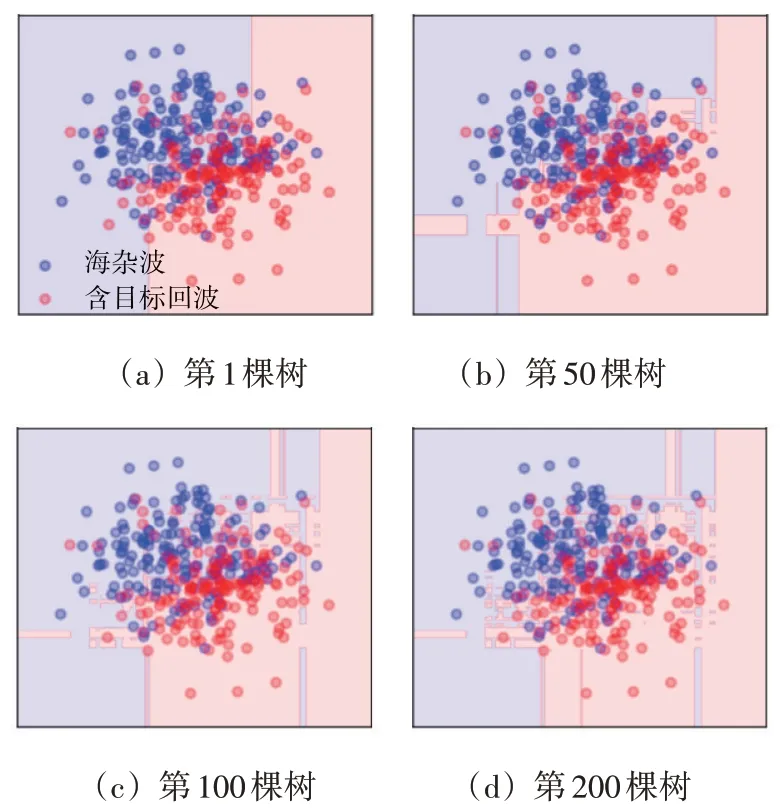
图4 二维特征空间中XGBoost分类器性能

接下来，在优先保证检测概率一定的前提下，尽可能地减小计算代价，从而找到合适的CART 树数目K和树最大深度D，如图5 所示。在图5（a）中，当K＜20 时，检测概率提升较为明显；当K＞50时，检测概率趋于稳定值。类似地，当D＞5 时，检测性能趋于稳定。从理论上来说，增加弱分类器数目和增大树深度，可以提升分类器的性能，但同时带来了更为复杂的计算量。在实际雷达探测环境中，可根据不同的性能要求，设置合适的参数。在本文中，综合考虑计算量和检测性能，确定参数K=100，D=6。

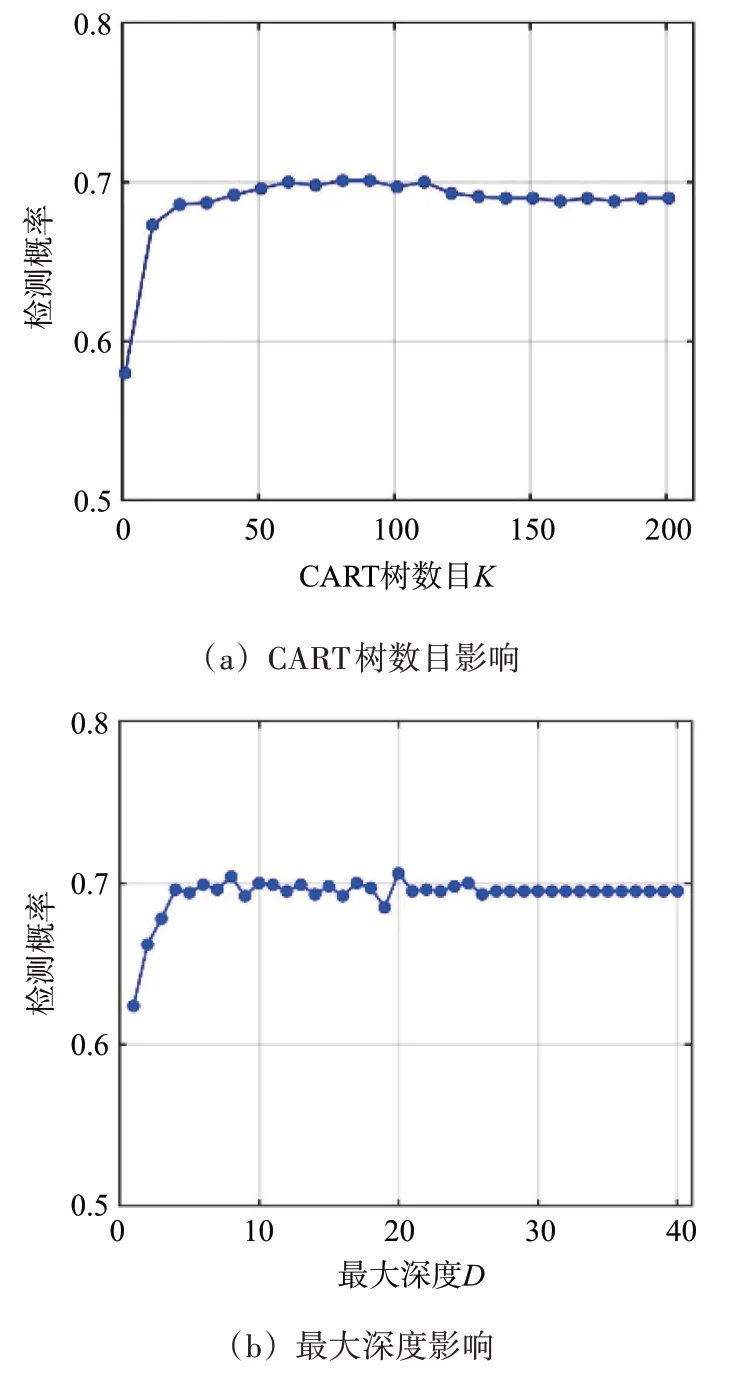
图5 两个结构参数对检测性能的影响

3.2 不同探测环境下性能分析

下面，使用实测数据验证基于多重虚警控制XGBoost 检测器的性能。设置脉冲累积数N=512（观测时间0.512 s），参考单元P=9，虚警率Pfa=10-3，分类器参数按照3.1 节中设置。由于每组数据都含有HH、HV、VH、VV 四种极化，10 组实测数据有40 个检测概率值。在图6 中，交叉极化（HV/VH）的检测性能优于同极化（HH/VV）的检测概率，这是因为不同极化下数据的信杂比不同。对于两个单特征检测器，基于Hurst 指数检测器［6］和基于全维度Hurst 指数检测器［9］在40 组数据上的平均检测概率分别为0.33 和0.55。虽然基于全维度Hurst指数检测器［9］融合了实数、复数、相位三个维度的分形特性提升了性能，但其性能依然受限制于单个特征的瓶颈。相对于单特征检测器，基于三特征检测器［10］、基于时频三特征检测器［11］和基于极化三特征检测器［12］的性能提升明显，整体平均检测概率分别为0.65，0.70，0.53，这来源于维度的增益和特征的有效性。鉴于3 个特征检测器维度相同，因而性能的差异性在于特征的不同。观察不同数据下的检测概率，不同特征组合的性能有较大的起伏性，这意味着有必要联合更多的特征。然而，本文提出的基于双重虚警控制XGBoost 检测器的平均检测概率为0.83，在不同数据下、不同极化下都具有最优的检测性能。这种性能优势充分体现了7个特征互补特性，保证了检测器在不同杂波环境、不同信杂比、不同极化下具有稳健的性能优势。

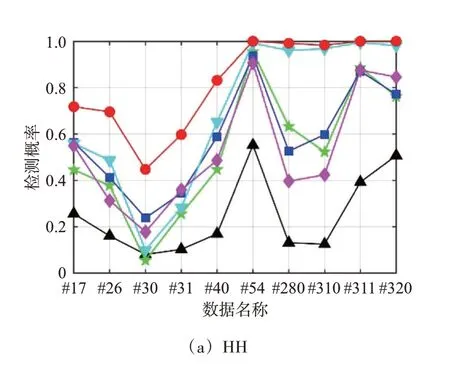
图6 不同数据下6种检测器的性能对比（N=512,Pfa=10-3）

为了充分验证检测器的通用性能，图7 和图8讨论了6 种检测器在1998 年数据#163113 下的检测性能。图7（a）是HH极化下在时间-距离上功率图，总观测时长为60 s，杂波功率起伏明显。测试目标位于第24 个距离单元，平均SCR 为-3.5 dB，因而从功率图上几乎看不到测试目标。在图7（b）的时频图中，小目标的瞬时频率曲线呈蛇形在零频附近波动，这是由于测试目标随海浪上下起伏导致的。海杂波的主杂波带位于（0 Hz,250 Hz）范围内，在整个观测时间内呈现出明显的非平稳特性。在图8（a）中，基于Hurst 指数检测器［6］的检测概率为0.11，在SCR低和秒级以内观测时间的条件下，性能损失严重。在图8（b）中，基于全维度Hurst 指数检测器［9］的检测概率为0.34，多维度信息量增多，检测性能有所提升。在图8（c）～（e）中，基于三特征检测器［10］、基于时频三特征检测器［11］、基于极化三特征检测器［12］的检测概率分别为0.59，0.62，0.68，性能进一步提升。在图8（f）中，基于双重虚警控制XGBoost 检测器的检测概率为0.81，具有最佳的性能。在第24 个距离单元上，小目标的运动轨迹较为清晰。

图7 实测数据（#163113）的时域和时频域特性

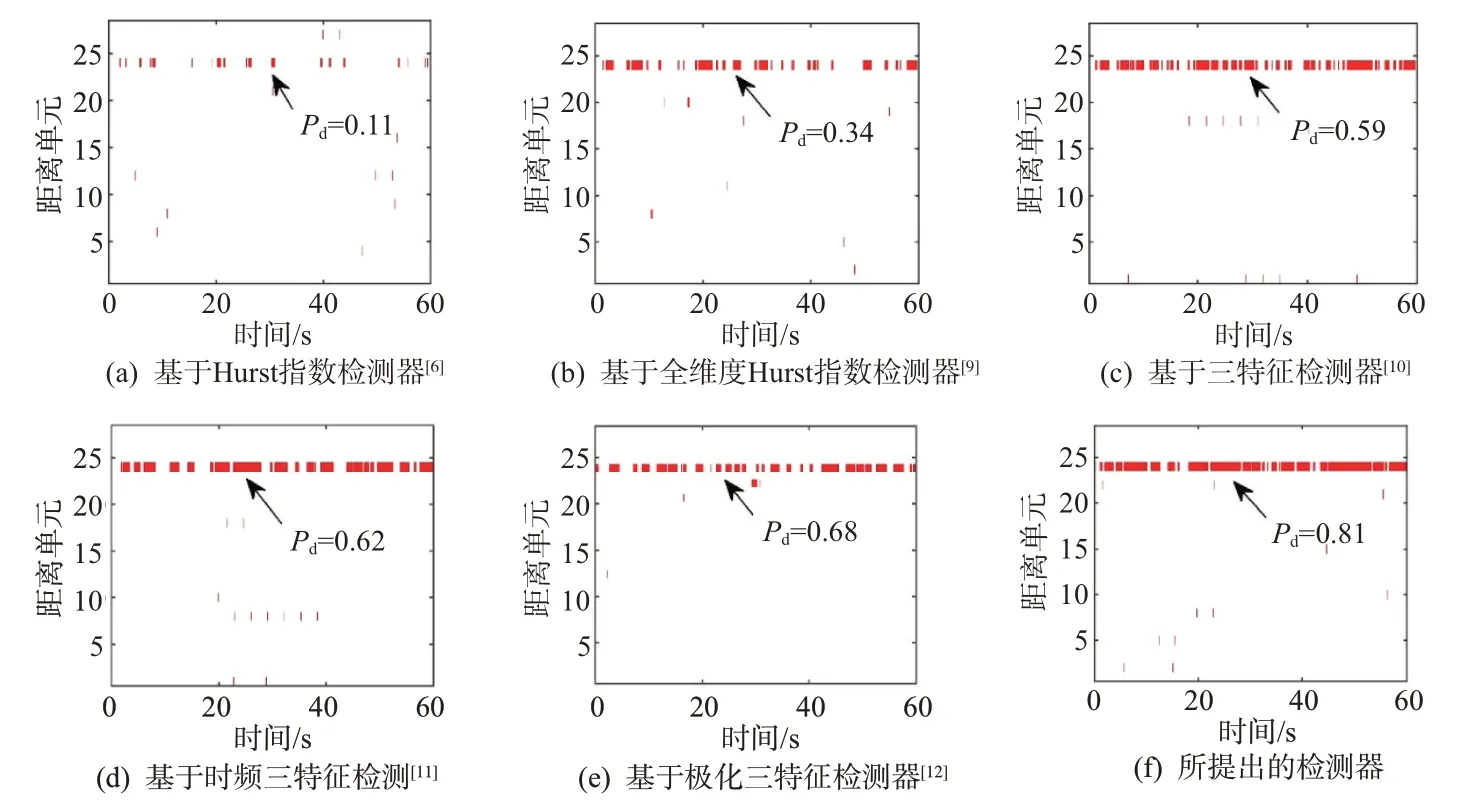
图8 6种检测器的检测结果（N=512，Pfa=10-3）

最后，讨论高维特征空间中两分类器的性能差异性。为了对比的公平性，4 种检测器都采用相同的七维特征，只有两分类器不同，其他参数设置与上述实验条件一致。为了方便讨论，将每组数据的4 种极化方式，独立为一组数据，因而共40 组数据。在图9（a）中，KNN 分类器［13］、RF 分类器［15］、SVM 分类器［16］和改进的XGBoost 分类器的平均检测性能分别为0.71，0.75，0.77，0.80，性能明显优于低维特征检测器。在4 种分类器中，改进的XGBoost 分类器的性能最优，这主要得益于弱分类器集成的优势和结构中两类惩罚因子的引入。在图9（b）中，4 种分类器的平均虚警率为0.001，都满足虚警设定值。但是，在不同的数据上，KNN 分类器［13］、RF 分类器［15］和SVM 分类器［16］的虚警率明显存在波动性，只有少数的数据上能够实现精准控制虚警率。主要原因在于3 个分类器都需要搜索与虚警率匹配的参数，参数的精度势必影响虚警率，存在一定的误差。然而，采用双重虚警控制的XGBoost 分类器，能够精准控制虚警率，满足雷达检测的需求。

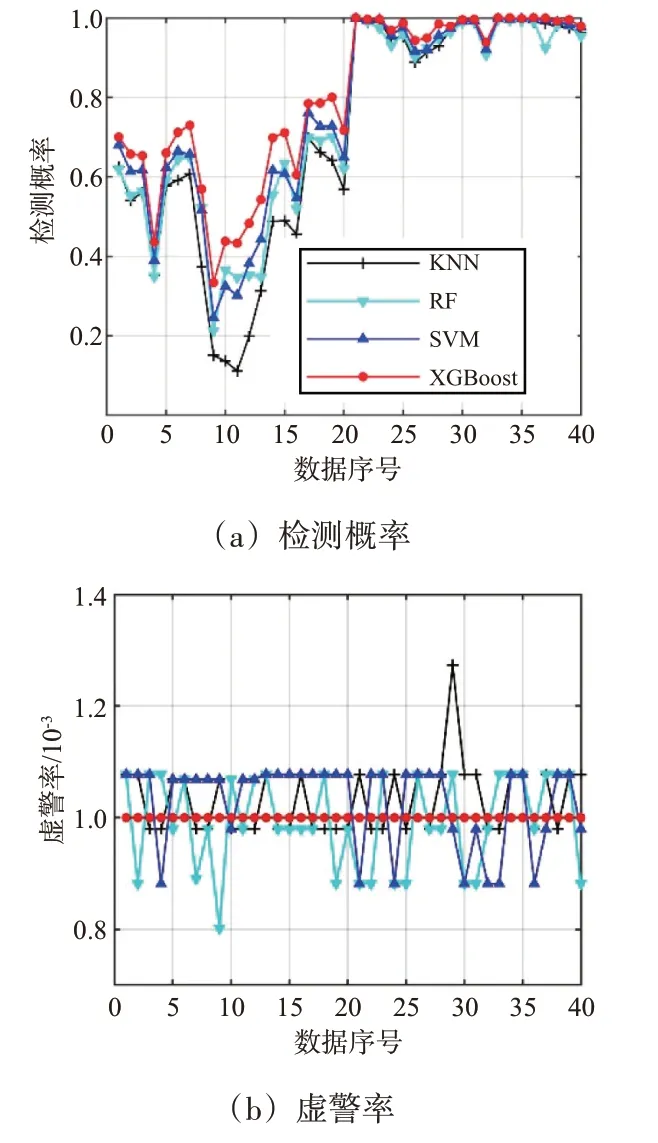
图9 高维特征空间中两分类器的性能对比（N=512,Pfa=10-3）

相较于KNN、SVM 等分类器，本文提出的改进XGBoost 分类器具有更多模型参数，但是并不明显需要更多训练样本。在固定虚警率Pfa=0.1 下，图10 给出了3 种分类器所需的训练样本数情况。第一，随着训练样本数目的增加，3 种分类器的性能都有提升，但提升空间是有限的。当样本数目大于500时，3种分类器的性能都趋于稳定，这意味着分类器已完全学到两类样本的特性。第二，为了保证可控的虚警率，KNN、SVM、改进XGBoost 分类器分别需要样本数目达到1 000、500、800 以上。KNN 分类器虽然本身参数较少，但是必须不断地调节参数k值以到达给定虚警率，这种全局搜索的方式势必要求大量的训练样本。不同于KNN 分类器，SVM 和改进XGBoost分类器是通过内部结构进行搜索参数，这种局部搜索的方式需要的样本数目明显减少。此外，根据Monte-Carlo 试验要求，在虚警率Pfa=0.001下，至少需要训练样本数目达到万以上。实验中，每组数据的训练样本数目为20 420个，如此大的训练样本完全可以保证3种分类器的性能达到稳定状态。因此，综合考虑分类器性能和虚警控制特性，3 种分类器的训练样本数目需求处于同一数量级。同时，由于创新性地引入了两个惩罚因子，不仅从结构上控制了虚警率，而且加快了XGBoost可控虚警的参数搜索，从而缩短了训练时间且保证了检测性能的提升。

图10 检测性能随训练样本数变化的情况对比

4 结束语

本文提出一种基于双重虚警控制XGBoost 的海面小目标检测方法，解决高维特征空间中两分类器的虚警控制问题，实现海面小目标性能的提升。从分类器的结构和参数两个层面，实现两分类器具有粗控和精控的双重虚警控制。实测数据验证了所提检测器的性能优势，主要得益于多个互补特征的联合以及分类器中两类错误率非均衡的结构。后续研究中可从结构层面直接实现精准的虚警控制，期望降低分类器的复杂度。