基于时延陷波FXLMS算法的自适应APF设计∗

徐亦杰 陈 亮 杨春宇

（中国舰船研究设计中心电磁兼容性实验室 武汉 430064）

1 引言

电力电子装置已经在电力系统中得到广泛的应用，交直流变换以及各种发电和用电设备并网都可以看到电力电子装置的身影。但是电力电子装置并非是百利而无一害的，电力电子器件本质是高速电子开关，工作时会产生很高的电压和电流变化率，由于寄生参数的存在，会在电回路中产生噪声，给电网带来了大量谐波［1］，造成用电设备的异常工作，危害设备的安全可靠运行［2］。

最早的有源电力滤波器（Active Power Filter，APF）由Sasaki H 在1971 年提出［3］，并在Akagi 于1982 年提出瞬时无功理论［4］后得到迅速发展。与此同时，新型全控型大功率电力电子开关器件进入实用阶段，再加上数字电路逐渐往高集成度的方向发展，能够实现更复杂的控制技术，使有源电力滤波器真正进入了工业实用阶段。现在APF 常用的控制方法有双PI 环控制、滞环电流控制、滑膜控制、无差拍控制、重复控制、预测控制、模糊控制、人工神经网络控制等。在此基础上研究出了大量的改进控制方式，例如Pandove 等对重复控制器灵敏度函数进行了平方修正，通过降低高频范围内的增益来解决高频不稳定问题［5］；Bosch 等在普通PI 控制器上额外增加预测控制和应对参数变化的附加校正补偿结构，在取得较好补偿效果的同时耗费较少的计算量［6］；曹武等采用过采样数字控制滞环电流跟踪以稳定开关频率［7］等。

截至目前，APF的研究主要针对陆上三相交流电网［8］，关注的谐波均为50Hz 基波的倍频，缺乏适用于船用直流电网的APF。船用直流电网的主谐波频率高达数千赫兹［9］，并且其高阶谐波在几千至十几千赫兹均有分布。传统的APF 检测并跟踪谐波的时域波形，然后输出与谐波幅值相等、相位相反的抵消信号，动态抵消谐波电流。但是基于时域信号对谐波进行跟踪抑制，会受到运算时硬件的固有延时的影响［10］，无法准确跟踪高频率的谐波。本文选取时延陷波的滤波-x 最小均方（FXLMS）算法作为自适应APF的控制算法，使设计的自适应APF能够实现参数的实时迭代更新，从频域的角度抵消主频率为数千赫兹的高频谐波电流。

2 基本原理及理论分析

2.1 LMS算法的工作原理

自适应滤波算法从原理上可以分为两类，即最小均方算法（LMS）和最小二乘算法（RLS）。本文涉及的LMS算法［11］基于梯度下降规则，沿均方误差曲面的最陡方向寻找使误差信号的期望均方差值最小的最优权值系数。其原理框图如图1所示。

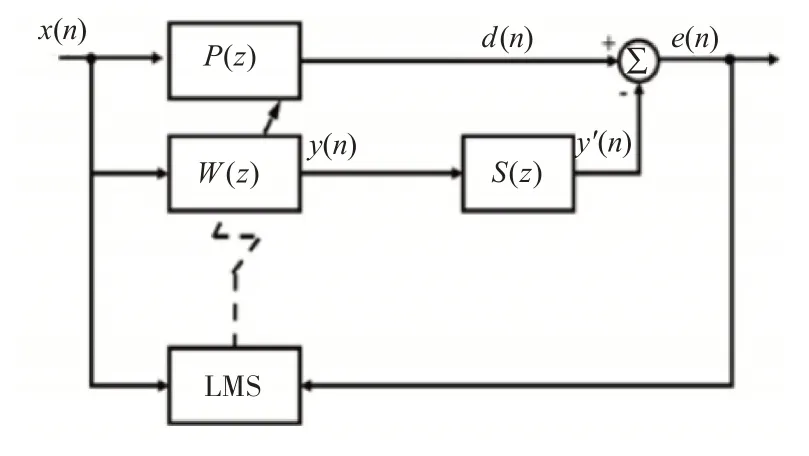
图1 LMS算法原理框图

P(z)为主通道，包含噪声源至误差信号检测点之间的物理通道，S(z)为次级通道，包含控制信号输出点至误差信号检测点之间的物理通道。算法的输入信号为参考信号x(n)、误差信号e(n)，输出信号为滤波信号y(n)。具体定义如下：

定义W(n)为滤波器权值系数：

将初始激励以一定的采样率进行采样产生序列x(n)，称为参考信号：

其中n 表示采样时刻，L 为控制器长度。n 时刻，滤波器输出y(n)为

误差信号e(n) 可表示为

按照最小均方误差准则定义目标函数可表示为

权值系数使用梯度下降法进行更新，使滤波器权值系数的每一步变化都正比于均方误差的梯度矢量的负值。自适应滤波器权值系数矢量的更新方式为

其中∇W(n)是权值系数更新的梯度因子，μ是为提高算法收敛性能而引入的收敛步长。∇W(n)的计算很困难，实际使用中，由于E[e2(n)]难以计算，所以通常采用瞬时值e2(n)作为估计值，通过快速迭代计算来达到无偏估计的效果。替换后可以计算出∇W(n)的估计值(n)：

合并常数项后得到权值系数的更新公式为

由式（7）可知，在权值系数W(n)更新的过程中是用瞬时平方误差对权值系数求偏导，若系统返回的误差信号e(n)和送入算法的参考信号x(n)并不处于同一时刻，求得的梯度方向就会出现偏差，偏差较小时会影响算法的收敛速度，当求得的矢量方向与下降梯度的矢量方向相位偏差大于90°时算法就会出现不稳定［12］，这种不稳定与传统闭环系统中相频特性小于-180°是类似的。

2.2 陷波FXLMS算法的工作原理

FXLMS 算法［13］由经典的LMS 算法发展而来，在主动噪声控制（ANC）领域取得了广泛的应用［12］，是一种经典的降噪算法。FXLMS 算法相较于LMS算法添加了次级通道S(z)的概念，对控制信号从发出到取得系统反馈的相位延迟进行了补偿。陷波FXLMS 算法是经典FXLMS 算法的一种陷波改进型，其原理框图如图2 所示。该算法的信号处理通道一次只能处理一个频率，多频点的复合谐波需要多个通道并行运算处理。从结构上来说，陷波FXLMS 算法的一个通道相当于一个正交的两阶陷波滤波器，即式（1）中的控制器长度L为2。

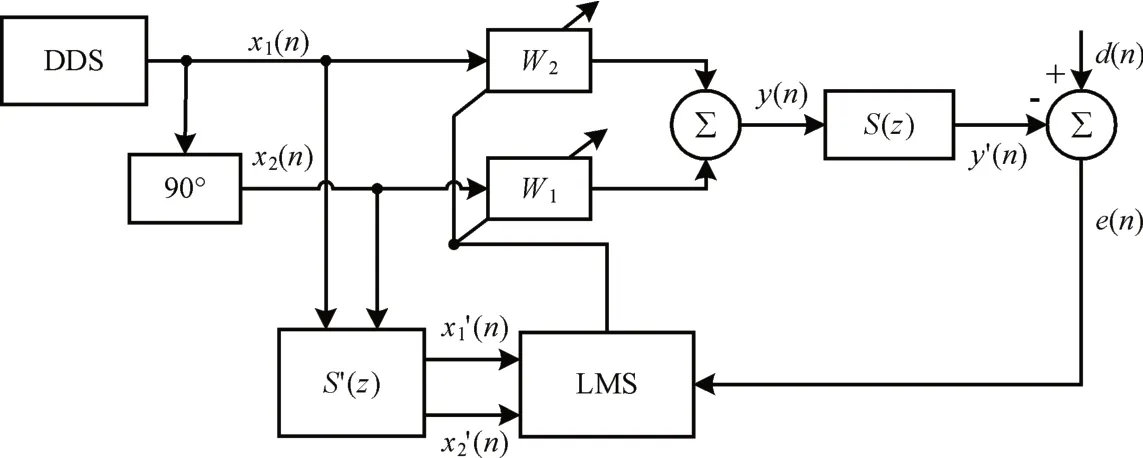
图2 陷波FXLMS算法原理框图

图2 中W1和W2为陷波权值系数。参考信号x(n)由内部的信号发生器，直接数字式频率合成器（DDS）产生。对于已知谐波频率的情况可以直接使用该频率值，若该频率未知，则需要检测谐波频率成分。假设该频率为f，幅值为A，则参考信号x(n)为

经过滤波器对应的输出信号为

用M 阶有限冲击响应（FIR）滤波器S'(n)对真实的次级通道S(z)进行估计：

在实际使用中，通常采用附加白噪声法对次级通道的传递函数进行离线建模［14］。假设滤波器S'(n)对次级通道S(z) 的估计不存在辨识误差。式（4）应改写为

设参考输入信号具有局部平稳性，使权值系数在L 个采样时间段内基本维持不变。则式（13）的后半部分可以改写为

式中x'(n)称为滤波参考信号，是输入信号x(n)与次级通道估算值S'(n)的卷积。

在FXLMS 算法的框架下，主通道权值系数更新方式为

式中μ为收敛步长。

2.3 以时延方式替代次级通道卷积

由式（14）可知，参考信号x(n)需要与次级通道权值系数S'(n)求卷积，以补偿次级通道带来的幅值和相位影响，所以当次级通道阶数较高时仍然具有很大的计算量，可采用时延的方式代替卷积运算［15］，以减小计算量。具体的实现方式为将单位脉冲响应函数（在本文中对应次级通道建模得到的权值系数），进行快速傅里叶分解（FFT）后得到相频特性P(f)，由于延时必须为正数，调整P(f)的值处于-2π～0之间。相位φ与时延t 有如下关系：

式中f 为信号源频率。可得延时的具体时钟周期数为

式中fs为数字电路的工作时钟频率，本文中根据硬件性能设为400kHz。

将d(f)的值以表的形式存储到数字控制系统的存储器，以当前信号源频率值f 为地址进行查表得到对应频率的延迟时钟周期数。对内部DDS 信号源合成的正弦波、余弦波进行延时操作后送入算法作为参考信号x(n)。

影响算法稳定性的是次级通道带来的相位误差，而幅值变化只影响收敛速度，因此时延可以替代次级通道的卷积运算。

3 基于时延陷波FXLMS算法的APF设计

3.1 APF整体结构

APF的整体结构如图3所示。APF并联接入船用直流电网。

图3 APF拓扑结构示意图

图3中各模块的功能如下。

1）参考信号从注入点的谐波源一侧采样送入预处理模块；

2）误差信号从注入点的负载一侧采样送入预处理模块；

3）预处理模块通过对参考信号进行FFT 运算获得谐波的频率成分，向算法模块发送幅值最高的若干频点，并使用积分电路和低通滤波等处理时域误差信号向算法模块发送；

4）算法模块负责计算指令电流，其详细结构如图4所示；

5）逆变模块采用单相全桥电路，使用正弦脉宽调制（SPWM）方式跟踪送入的指令电流信号；

6）注入模块包括隔直电容和缓冲电路等。

图4 以三频点谐波工况为例，设置了三个并行处理的陷波通道。其中误差信号和DDS 信号的频率值由前一级的预处理模块发送，输出的指令电流信号发送至逆变模块。每个陷波通道独立工作，基于LMS 算法的梯度下降规则对权值系数进行更新，各通道的输出信号再叠加形成总输出，对多频点的目标谐波进行抑制。

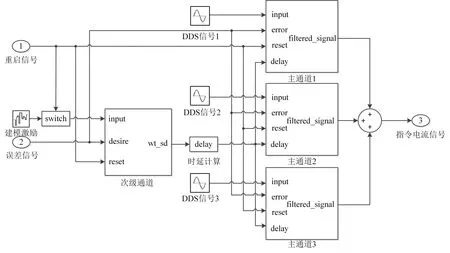
图4 时延陷波FXLMS算法模块结构示意图

3.2 时延陷波FXLMS算法软件设计

本文的现场可编辑逻辑门阵列（FPGA）采用Verilog 语言进行编程。Verilog 语言是一种自上而下的硬件描述语言，需要将控制算法分为几个模块进行编写，顶层模块通过调用各个子模块来实现算法功能。本文的设计思路如图5所示。

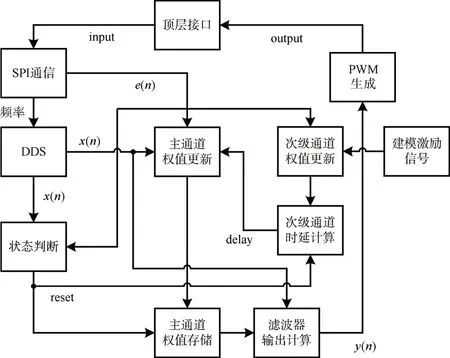
图5 时延陷波FXLMS算法FPGA程序设计思路

由于200MHz 系统时钟频率很高，首先通过分频或定时器的方式获取400kHz 的工作时钟。本文采用定时器的方式生成400kHz 的工作时钟，包括算法权值系数更新、AD 芯片采样及读取、PWM波生成等操作均以工作时钟触发步进。

除了算法本身的各组成模块之外，还有若干用于通信的辅助模块。例如与AD 芯片进行通信的串行外设接口（SPI）模块以及与微控制单元（MCU）进行通信的SPI 模块。AD 芯片通过三线SPI 通信向FPGA 周期性发送误差信号e(n)，MCU 通过四线SPI 向FPGA 发送谐波幅值最高的数个频率值，并兼有与上位机通信的功能。

4 试验平台搭建及试验结果分析

试验装置的基础架构如图6所示。

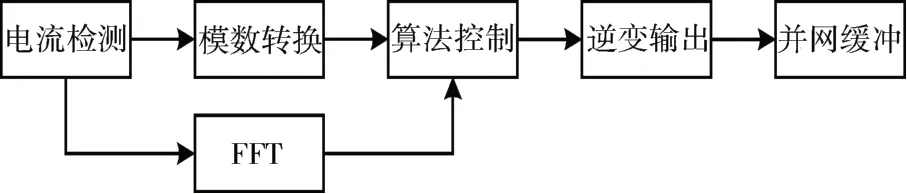
图6 APF装置基础架构

该装置可分为以下几个环节：

1）电流检测环节采用罗氏线圈配合积分电路以及低通滤波器检测谐波电流。谐波电流的模拟量送至模数转换环节。

2）模数转换环节。本文采用的AD芯片分辨率为16 位，实际使用采样率400kHz。AD 芯片与FP⁃GA 之间采用SPI 通信，将谐波电流的数字信号发送至算法控制环节。由于没有双向通信需求，采用三线SPI通信。

3）算法控制环节。本文中的FPGA 系统时钟频率200MHz，工作频率400kHz。参考信号的频率值由MCU进行FFT计算并通过SPI通信传输给FP⁃GA。FPGA 基于时延陷波FXLMS 算法计算指令电流并转换成PMW波送至逆变输出环节。

4）逆变输出环节。逆变器的开关管选用能适应400kHz高速开断的MOS管。本文的背景是消除电力电子设备产生的谐波，因此逆变器的开关器件的开关频率必须要远高于谐波源。拓扑结构采用48V直流电源的单相全桥电路。

5）并网缓冲环节。为减小APF 并网时对电网的冲击，装置输出侧包含了隔直电容、隔离变压器以及缓冲电路。

谐波抑制试验平台主要包括干扰源、负载电阻、控制模块、逆变模块等模块。干扰源使用信号发生器连接功放，形成谐波电压源。信号发生器应至少能同时生成三个频率的正弦波，以对多频点的工况进行试验验证。选取5kHz、10kHz、15kHz 为例，设置信号发生器并叠加输出至功放。调整干扰源的大小至0.1Ω 负载电阻上产生的干扰电流幅值为10A。为保证罗氏线圈的检测值准确、稳定，临时采用了塑料瓶确保载流导线从线圈中心轴心通过。正式使用时应固定罗氏线圈与电网母线的相对位置，使电流从罗氏线圈的中心轴线流过。罗氏线圈检测到干扰谐波电流后经过低通滤波以及放大后，送给AD 芯片作为误差信号。试验平台的搭建示意图如图7所示。

图7 有源电力滤波器试验平台

完成平台搭建后，通过合适的探头，对谐波电流进行检测，连接频谱仪获取频域的抑制效果对比，结果如图8所示。

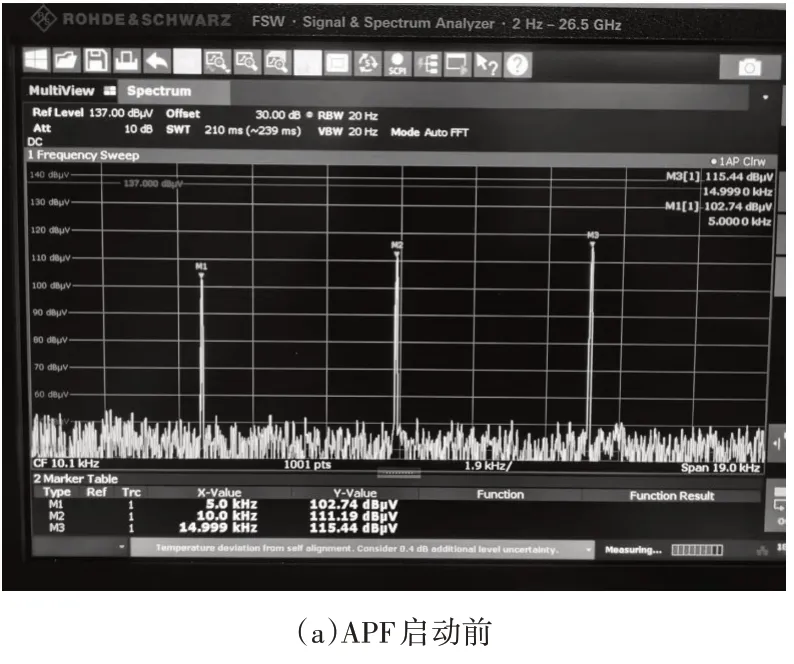
图8 谐波电流抑制效果频域对比图

抑制效果总结如表1所示。

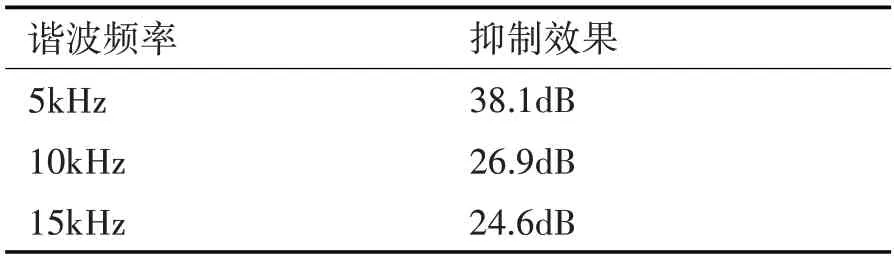
表1 APF启动前后谐波抑制效果对比

从频域对比可以看出，装置对5kHz、10kHz、15kHz 的复合频率谐波的三个频点均取得了24dB以上的抑制效果。APF 装置对预设谐波频率抑制效果均达到24dB 以上，实现了对高频谐波的有效抑制。

5 结语

针对缺乏适用于船用直流电网的APF的现状，分析并设计了基于时延陷波FXLMS 算法的自适应APF。搭建了基于FPGA的APF试验平台进行试验验证。根据原理，所设计的APF能抑制20kHz以内的若干个任意频点的谐波，频点越多则对硬件的要求越高。试验以5kHz、10kHz、15kHz的三频点复合频率谐波为例，APF装置对预设谐波频点抑制效果均达到24dB以上，实现了对高频谐波的有效抑制。