基于改进MILS的船舶操纵响应模型辨识∗
2023-08-04陈永冰李文魁
向 军 陈永冰 李文魁
(海军工程大学电气工程学院 武汉 430033)
1 引言
随着航运事业的发展,对船舶航向航迹控制的要求越来越高,而研究船舶操纵性与控制问题的基础是建立船舶运动数学模型[1]。这些模型中含有未知参数,考虑到船舶作为一个整体系统具有典型的时变非线性,即船舶载重、吃水、航速等发生变化时,其模型参数也会随之改变。因此采用系统辨识的方法实现对船舶航行过程中的未知模型参数的在线辨识具有重要意义。
目前,常用的辨识算法包括最小二乘法、最大似然估计、卡尔曼滤波、神经网络[2~3]、支持向量机[4~5]等;赵大明[6]等将船舶运动模型参数当作变量,建立增广状态方程并结合扩展卡尔曼滤波算法进行参数辨识,取得了良好的辨识效果;秦操[7]利用无迹卡尔曼滤波在非线性系统滤波中的精确性,将其应用了到三体船的MMG运动数学模型参数辨识中;秦余钢等[8]引入一种新的学习率对递推最小二乘算法进行改进,提高了船舶操纵性参数辨识的精度和速度;张显库等[9]提出一种基于正弦函数处理非线性新息的最小二乘算法,改进了最小二乘算法的准确性;褚式新等[10]采用极大似然法辨识水面无人艇的操纵响应模型参数,利用辨识结果对无人艇的操纵性进行了精准预报;谢朔等[11]针对船舶操纵运动模型参数辨识问题,将最小二乘向量机递推算法中的单新息扩展为多新息,提高了辨识精度;以上研究重点集中在辨识数据激励充分的条件下,提高参数辨识的精度,而对辨识数据欠激励的情况考虑不足。输入激励对于参数辨识性能有较大的影响,当前用于辨识船舶模型参数的实验数据通常来自于船舶的回转、Z 型试验,这些数据满足持续激励的条件,使得辨识结果能很好地收敛于真值。但在实际的船舶航行控制过程中,有直航与转弯的情况,输入舵角在小幅度范围内变化甚至保持不变,这就导致所得数据激励不够充分,大大影响了参数辨识的收敛性和准确性。
针对上述问题,包政凯等[12]利用满秩分解思想解决了最小二乘算法中矩阵奇异不可逆的问题,成功应用到船舶航向运动模型参数辨识中,但其未能对非线性参数进行辨识,辨识结果不具备通用性。本文将奇异值分解(SVD)技术[13~15]与多新息理论[16]引入最小二乘法(Least Square Algorithm,LS)中,提出一种改进的多新息最小二乘法。该算法利用奇异值分解的数值稳定性,使其在船舶正常航行过程中小幅度短暂打舵的情况下仍能具有较好的收敛性与辨识精度,将辨识所得船舶模型用于操纵运动预报,并与实际试验数据进行对比,验证了该算法在线辨识船舶操纵响应模型参数的有效性。
2 船舶操纵响应模型
水动力模型与响应型模型是船舶运动模型的两大类别[17],水动力模型对船舶自身运动特性和所受外力影响进行了详细描述,能够对船舶运动进行较为准确的预报,但该模型中含有大量未知水动力参数,计算复杂且不易获取。响应型模型参数较少,其主要描述了艏向角速度与舵角之间的变化关系,在船舶的运动控制器设计和操纵运动特性预报中应用最为广泛,其表达式为
式(1)中:r为船舶艏向角速度;δ为舵角;K、T为回转性指数和应舵指数,它们近似体现了船舶在某种速度下,船舶角速度与舵角之间的关系,受到船舶的航速与载荷条件的影响;
该模型为船舶一阶响应线性模型,考虑到船舶具有非线性特性,故增加一个非线性项αr3,其中α为非线性项系数,则得到的船舶操纵响应一阶非线性模型为
为了便于模型参数辨识,将式(2)进行前向差分离散化可得:
式(3)中,Δt为采样间隔。令1-Δt/T=a,-αΔt/T=b,KΔt/T=c,可得:
式(4)中,a、b、c即为待辨识参数。
令y(t)=r(t+1),h(t)=[r(t),r3(t),δ(t)],θ(t)=[a,b,c]T,则式(4)可化为
该式即为船舶操纵响应模型的最小二乘回归形式,后续的辨识算法表达式也是基于此式展开。
3 改进MILS算法设计
3.1 多新息最小二乘算法
递推最小二乘算法具有结构简单、计算快捷的特点,是应用最为广泛的系统辨识算法。它的标准表现形式为
式(6)中:P(t)为协方差阵;K(t)为增益向量;e(t)为每次递推时的新息标量,即单新息;为t时刻θ的估计值。为使算法启动,需要确定协方差阵和待辨识参数向量的初始值,一般人为给定经验值如下:
式(7)中:α2很大,一般取106~1010;I为单位阵。
多新息最小二乘辨识算法是递推最小二乘法与多新息理论结合形成的新算法,该算法可以不断重复使用历史数据,收敛速度和辨识精度都得到了改善。其原理是将单新息标量e(t)拓展为多新息矩阵E(p,t),即
考虑到矩阵维数的兼容性,信息向量和输出向量拓展为
由此,该算法表达式由式(6)变为
式(10)中:p为新息长度,根据该长度取初始的一小段试验数据,进行单新息最小二乘估计,将得到的协方差阵和参数向量的值作为初始值。
3.2 多新息最小二乘算法的改进
在辨识数据欠激励的情况下,随着计算误差的传递和累积,辨识精度将越来越低,从而导致辨识算法难以收敛于真值。从式(10)中可以看出,协方差阵P(t)的计算是该算法的核心,为改善该矩阵的数值计算性质,本文利用SVD技术对其进行奇异值分解。具体推导如下:
先引入矩阵反演式:
利用矩阵反演式对式(10)中的协方差阵更新式进行变换可得:
由协方差阵的对称正定性,对其进行奇异值分解,则式(12)可表示为
构造矩阵Ω,其具体形式为
对该矩阵进行奇异值分解可得:
则
将式(16)代入式(13)中,根据正交矩阵的性质可化为
对比等式两端,则有:
通过上述推导,得到了协方差阵P(t)的奇异值分解矩阵U和D的递推公式,从而取代了P(t)的更新计算。
则增益矩阵K(t)的递推式变为
根据以上推导,改进多新息最小二乘算法的实现步骤可总结如下:
1)初始化协方差阵P、辨识参数向量θ;初始化奇异值分解后的矩阵U(0)=I、D(0)=
2)按照式(14)构造矩阵Ω。
3)按照式(15)对矩阵Ω 进行奇异值分解,得到其右奇异矩阵和奇异值。
4)按照式(18)更新U(t),D(t)。
5)按照式(19)对增益矩阵K(t)进行更新。
6)按照式(10)中的参数向量递推式对参数进行更新。
4 仿真验证与结果分析
4.1 辨识数据采集
本文以文献[18]中的某型船舶为研究对象,建立式(1)的一阶非线性响应模型,其模型参数如表1所示。
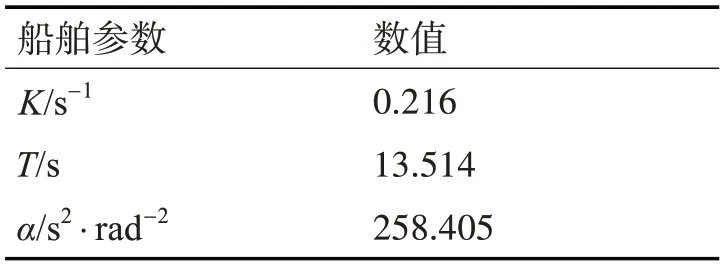
表1 某型船舶模型参数
为获取参数辨识所需的试验数据,验证辨识算法在数据欠激励情况下的辨识效果,利用已知的模型和参数在仿真软件Simulink 中做船舶自由航行的仿真实验,包括船舶直线航行与转向,仿真采样间隔为0.01s,采样时间为400s,得到的辨识数据如图1所示。
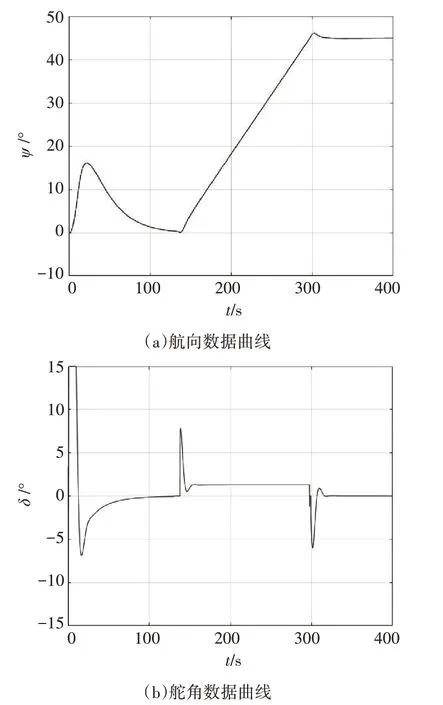
图1 辨识数据曲线
为证明舵角数据的真实性,通过单位实验室中的NP5400型自动舵与综合模拟平台进行了多次航向控制的模拟实验,采用自主设计的操舵仪综合训练与检测系统接收航向与舵角数据,如图2 和图3所示。其中图3 为某次常规的船舶航向控制实验中接收的实验数据。
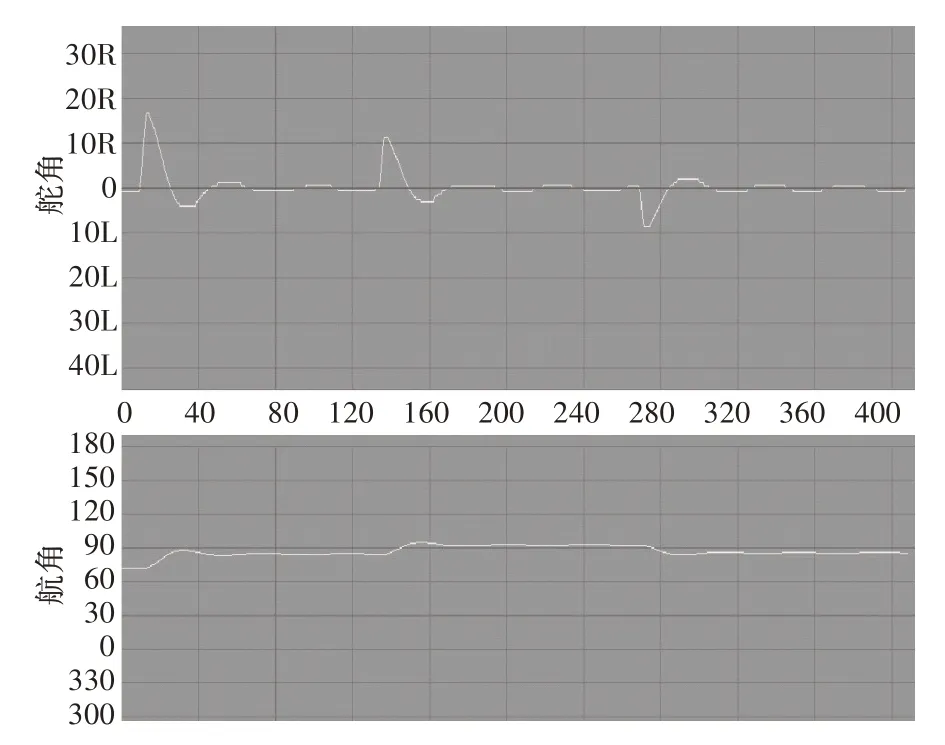
图3 某次常规船舶航向控制实验中接收的实验数据
从图中可以看出,当船舶航向变化15°时,打右舵17°,回舵后打左舵5°,从而实现航向的控制,故符合0s~50s 仿真数据中的打舵情况;同理,仿真数据中的右舵8°和左舵6°也符合实际情况,因此图1中的仿真数据可以作为船舶实际航行过程中接收的辨识数据。
4.2 船舶操纵响应模型参数辨识
根据数据激励程度差异,取采集的试验数据中0s~50s 和300s~350s 两段,先后选取这两段数据采用MILS 和改进MILS 对式(2)中的模型参数进行辨识,对比实验结果,分析在辨识数据欠激励的情况下,辨识算法的精确性和收敛性。
两种算法的新息数均设置为10,参数辨识结果对比曲线如图4~5所示。
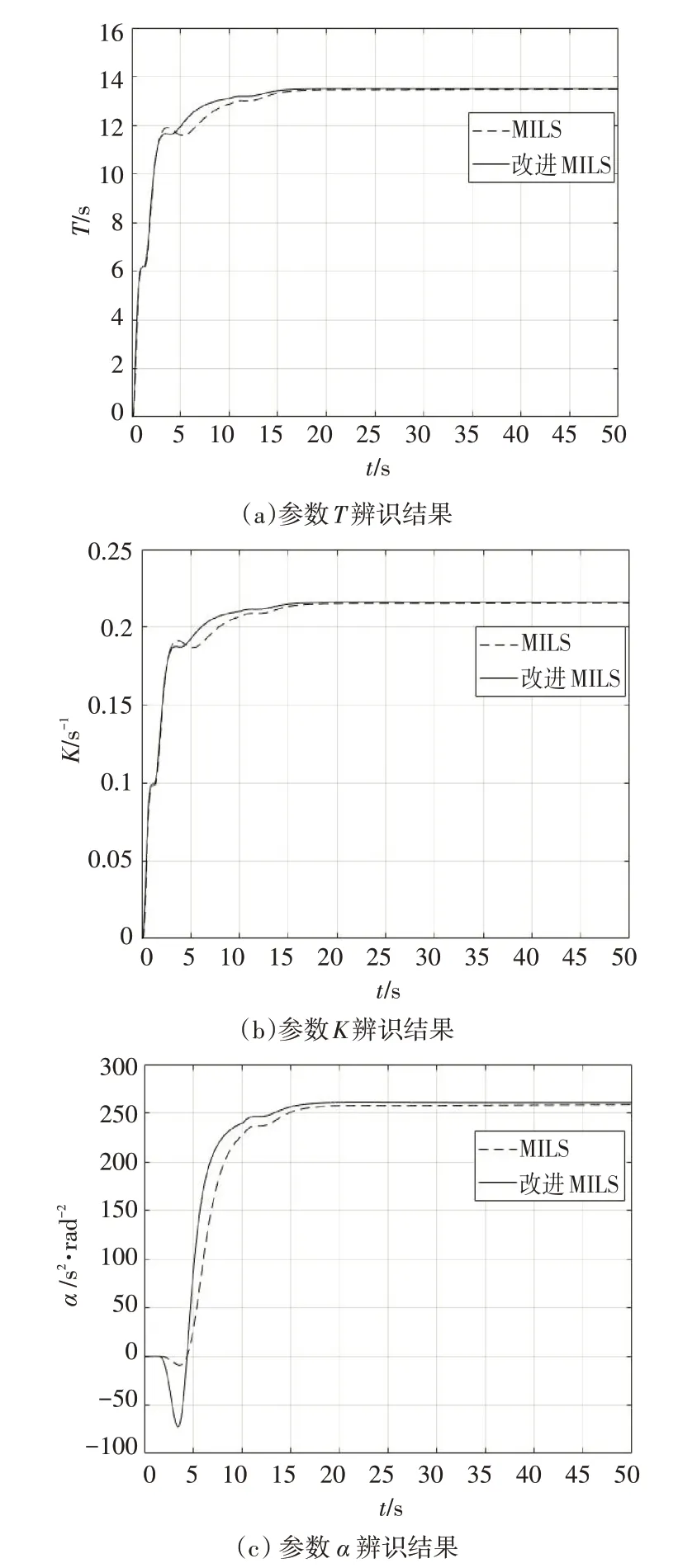
图4 各参数辨识结果曲线(0s~50s)
由图4和图5可以看出,在0s~50s辨识区间,船舶航向处于不断变化阶段,打舵时间长且范围在左舵6°和右舵15°之间,故辨识数据激励较充分,两种辨识算法的辨识结果均能快速收敛于真值;而在300s~350s 辨识区间,船舶打一次左舵6°且迅速回舵,右舵不到1°,辨识数据不满足持续充分激励的条件,此时MILS算法辨识的参数有偏,尤其是高次项系数α对激励的要求更高,辨识结果偏差严重,而改进MILS 算法在辨识数据欠激励的情况下,辨识精度明显高于MILS 算法且收敛较快。因此,引入奇异值分解提高了多新息最小二乘算法的辨识精度。欠激励情况下的参数辨识结果见表2。
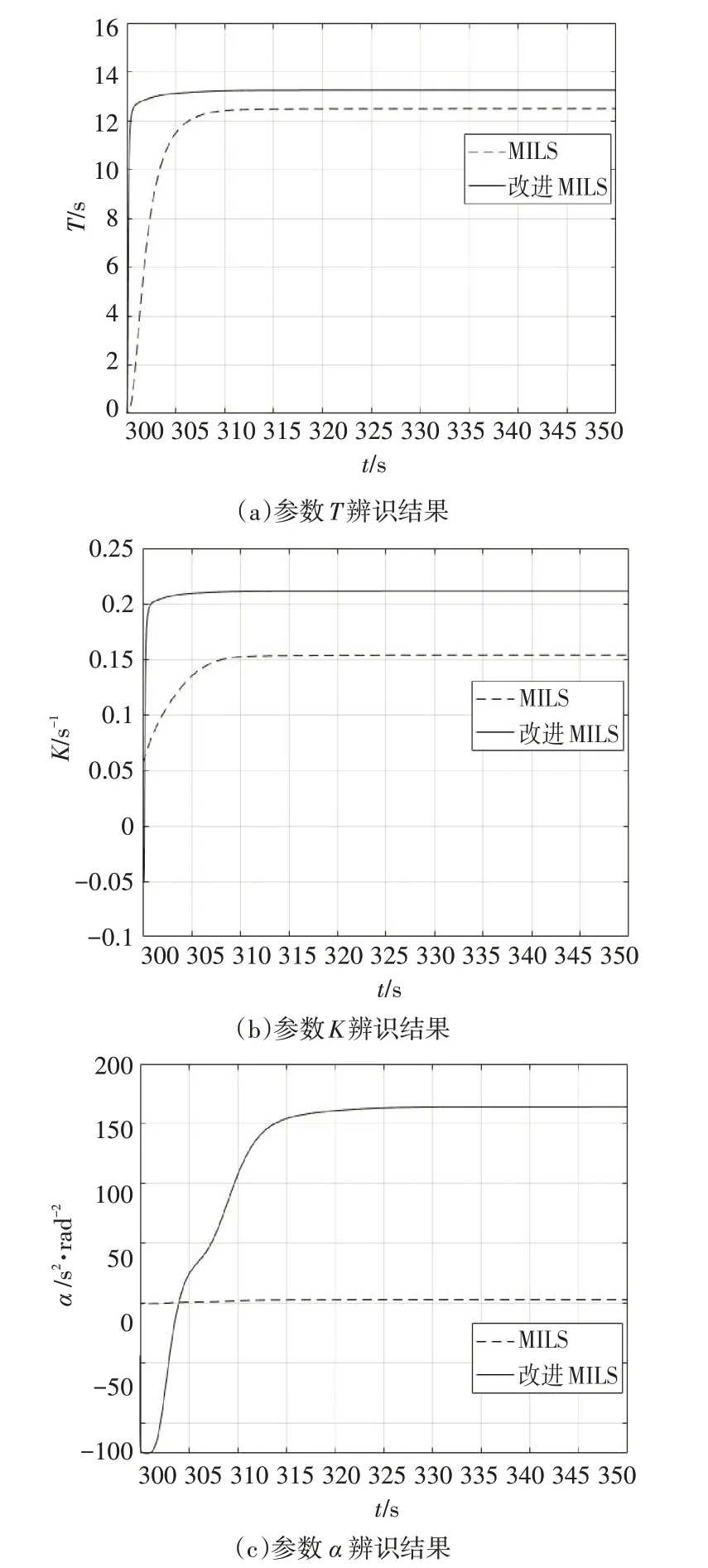
图5 各参数辨识结果曲线(300s~350s)
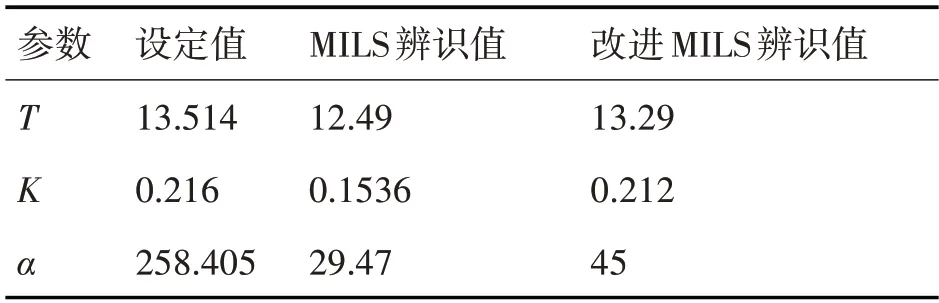
表2 参数辨识结果
由表2可知,MILS算法的辨识结果中,T、K、α的辨识误差分别为7.57%、28.89%、88.59%;而改进MILS 算法的辨识结果中T、K、α的辨识误差分别为1.65%、1.85%、82.58%。前者的平均误差达到了41.68%,后者平均误差为28.69%,降低了12.99%。
4.3 辨识模型运动预报
为了检验算法精度对船舶运动的影响程度,验证辨识算法的有效性。将参数辨识结果代入式(2)中,以船舶航行仿真试验中的舵角数据为输入,利用龙格-库塔法求解式(2)船舶响应模型,从而对船舶艏向角进行预报,预报时间为2000s。求解公式如下:
式中,yt=[r,ψ]T,f(t,yn)=[Kδ/T-r/T-αr3/T,r]T,th为采样周期,取th=0.01s;k1、k2、k3和k4为各时间段的斜率。将预报结果与实际仿真试验数据比较如图6所示。
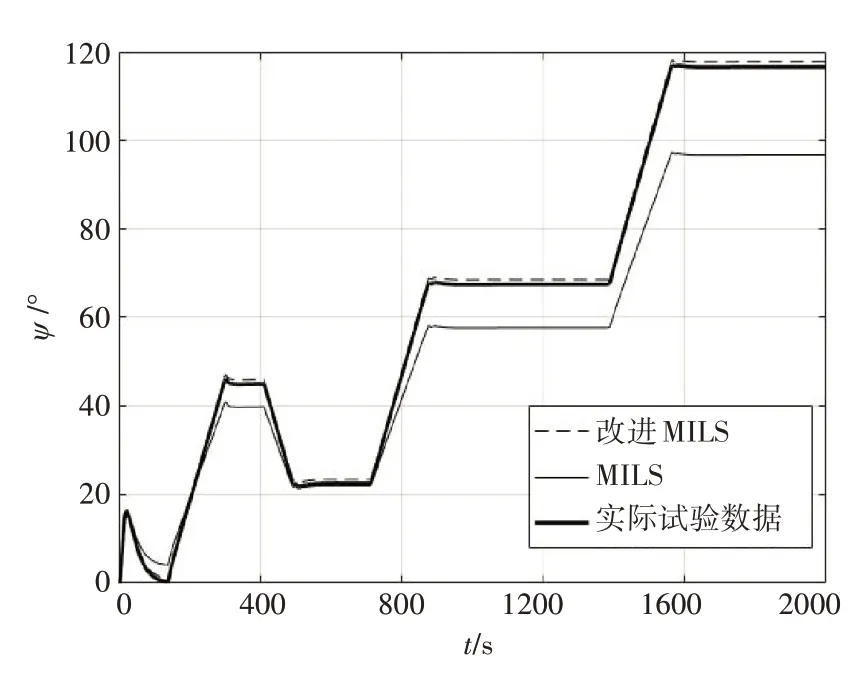
图6 艏向角预报曲线
从图6 可以看出,MILS 算法的航向预报值误差随时间不断叠加,而改进MILS 算法对船舶艏向角的预报值更接近真值,满足船舶航行的误差要求。
5 结语
本文将多新息理论与奇异值分解技术相结合,提出了一种改进MILS的模型参数辨识算法。通过仿真验证与对比分析,得到以下结论:
1)基于奇异值分解对MILS 算法进行改进,改善了数据欠激励情况下参数辨识不准的问题,辨识精度得到了有效提高,适用于船舶正常航行过程中小幅度短暂打舵情况下的参数辨识。
2)通过辨识得到的模型进行船舶航向的预报对比,该算法的航向预报满足误差要求,验证了算法的有效性。
本文辨识所使用的数据来自于仿真试验,不能完全保证算法的泛化性,后续可以使用实船试验数据来进一步验证。此外,还可以与自适应控制器设计相结合,进行船舶航向控制的研究。
