一种基于DQN的改进NSGA-II算法∗

吴亚楠 张 剑

（武汉数字工程研究所 武汉 430205）

1 引言

武器目标分配（Weapon Target Assignment，WTA）问题，又称导弹分配问题（Missile Assignment Prob⁃lem，MAP），起源于20 世纪50 年代［1］，是作战指挥控制系统所要解决的重点问题。武器目标分配方案是否实时、准确、有效，将直接影响军事对抗中能否取得更好的作战效能并尽量减少作战资源消耗［2］。

当前，已有多种方法可用于求解WTA 问题。其中，以NSGA-II 算法等为代表的智能优化算法［3～5］，以及由这些算法组合而成的混合优化算法［6～8］，是目前WTA 问题的主流求解方法。受算法本身原理机制的影响，直接将NSGA-II 算法应用于求解WTA 问题仍然存在无法规避的缺陷，如算法容易陷入局部最优、多样性不足。近年来，强化学习领域发展势头迅猛，有些学者开始思考将强化学习主动探索、不断试错的特性与传统优化算法结合的可能性［9～11］。封硕等［12］提出可采用双种群“迁徙思想”对传统单种群NSGA-II 算法进行改进，引入强化学习Q-learning 算法来对迁徙操作涉及到的相关参数m主动地进行优化，并通过实验验证了该做法可避免传统单种群NSGA-II算法陷入局部最优，解集具有更好的分布性，但其他两项迁徙参数p、q的设置对算法的最终结果同样起着重要的作用。

本文针对多类型反舰导弹攻击舰艇编队的WTA 问题进行研究，首先对数学建模过程进行简要介绍，分析海战场背景下可能影响分配方案结果的多项因素，建立多目标优化数学模型。为有效求解该模型，本文提出了基于深度强化学习的改进NSGA-II算法，采用深度强化学习和双种群“迁徙”思想对传统单种群NSGA-II算法进行改进，通过深度强化学习DQN 算法对迁徙操作涉及到的多个参数进行优化。仿真实验表明，与传统单种群NS⁃GA-II 算法、迁徙参数按照人类经验设置的普通双种群NSGA-II算法进行对比，本文所提出的基于深度强化学习的改进NSGA-II算法可提升算法性能，减少算法耗时，获得更好的分配方案集结果。

2 问题描述与建模

在复杂的海战场环境下，武器目标分配方案的形成一方面要考虑最大化对敌毁伤效果，另一方面要尽量减少弹药消耗。除此之外，还需考虑多个约束条件，如对单个目标所分配弹药上限、各类型反舰导弹总弹量、反舰导弹所搭载平台上火力通道数限制、反舰导弹作用距离限制等。只有全面细致地考虑代价和收益两方面因素，综合各项约束条件，才能反映真实的战场情况，得到更加科学、合理的武器—目标分配方案。因此，本文所研究的WTA问题实质上是一个多目标优化问题，如图1所示。

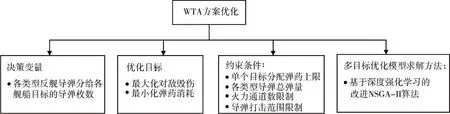
图1 WTA方案优化

3 改进NSGA-II算法用于求解弹目分配问题

3.1 DQN算法优化迁徙参数思想

文献［12］提出可采用双种群“迁徙思想”改善传统单种群NSGA-II算法的缺陷，首先设置两个独立种群1和种群2，令两种群分别进行遗传演化，在进化初期的前p 代每隔q 代令种群1 的前m 个精英个体和种群2 的随机m 个个体进行交换，交换后形成新的种群1和种群2，随后两种群继续寻优进化，直到达到终止条件。此时，共有p、q、m 三项迁徙参数需要确定，本文采用深度强化学习DQN 算法，通过智能体与环境的交互来同时对三项迁徙参数进行动态调整，进而提高算法性能，获得更好的Pareto最优方案集。

3.2 DQN算法要素设计

基于深度强化学习DQN 算法对传统单种群NSGA-II算法进行改进，首先必须用马尔可夫决策过程进行建模，对状态空间、动作空间、回报函数等进行设计。本文以种群1和种群2的当前收敛性与初始收敛性的比值、当前多样性与初始多样性的比值作为状态空间。选用七点平均距离SPAD［13］作为收敛性衡量指标，选用指标Δ*［14］作为多样性衡量指标。以三个迁徙参数p、q、m 的增大、减小、不变作为动作空间，根据状态设计相应的回报值，具体细节如下。

1）状态空间S

状态St表征当前种群收敛性、多样性与初始种群收敛性、多样性的比值，即St=(SPAD1_m/SPAD10,SPAD2_m/SPAD20,VAR1_m/VAR10,VAR2_m/VAR20)。其中，SPAD10、SPAD20、VAR10、VAR20 分别表示初始种群1、初始种群2的收敛性值、多样性值；SPAD1_m、SPAD2_m、VAR1_m、VAR2_m分别表示根据智能体动作获取三个迁徙参数值，并按照参数值在环境中执行完相应的迁徙操作后当前种群1、种群2的收敛性值、多样性值。

根据比值大小，状态的意义可分为与初始种群相比迁徙后数值增大、数值减小、数值保持不变，两个种群共有4 个比值，总共3×3×3×3=81 种组合方式，即81 种状态，目标状态为4 个比值均小于1（因收敛性衡量指标SPAD和多样性衡量指标Δ*均为值越小越好型），表示按照迁徙参数值执行相应的迁徙操作后，当前两种群的收敛性和多样性均优于初始两种群。

2）动作空间A

动作空间的动作设计为对p、q、m 三个迁徙参数大小的更改，如表1 所示。初始化种群的同时会随机设定三个参数大小在一定范围内，用p_random、q_random、m_random分别代表三个迁徙参数的初始值。动作空间的每一个动作是在三个参数原基础上进行增加、减少或保持不变，每个参数的改变量由事先设定，如A×popsize=10、B×popsize=1、C×popsize=2，其中popsize=100代表种群大小，A、B、C分别代表参数p、参数q、参数m的调整比例。

表1 迁徙参数调整

如表1 所示，动作空间共有1×3×3=9 个动作可供选择，其中参数p 的数值不可减小或保持不变，因参数p代表在前p代执行迁徙，而遗传操作一经执行不可逆转，故参数p只可增大。

3）回报函数R

本文优化的目的在于寻找p，q，m 三个参数的最佳值，以使得与之前种群相比，种群1和种群2的收敛性、多样性指标均有所改善。因此，对回报函数设计如下式所示。

当回报值Ri(i=1,2,3,4) 的值为0.5 时，代表执行迁徙动作后当前种群收敛性或多样性优于初始种群。

3.3 改进NSGA-II算法实现

将双种群NSGA-II算法主体部分作为环境，它将根据智能体选定的动作获取三项迁徙参数的值，在相应遗传代数执行迁徙操作，并根据当前迁徙操作的结果，将相应回报值返回至智能体。

主程序DQN算法实现步骤如表2所示，主要描述了算法如何进行动作选择、如何训练Q网络等细节。

表2 DQN算法实现步骤

环境更新部分的算法步骤如表3 所示，主要描述了环境如何根据智能体的动作获取相应的迁徙参数，对状态进行更新等。

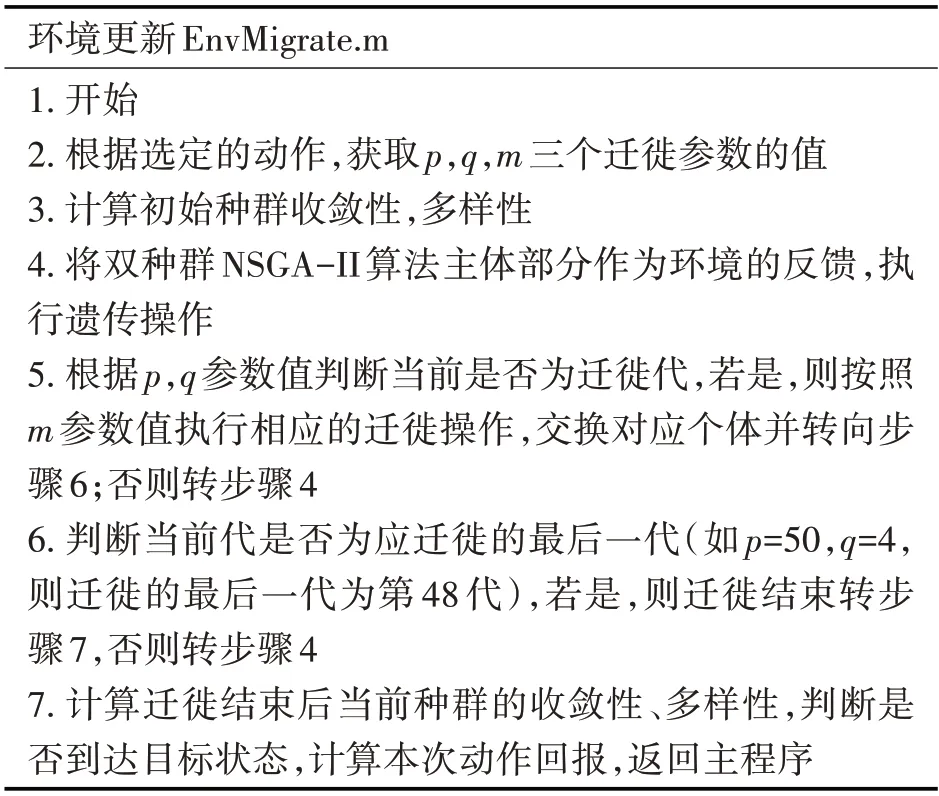
表3 环境更新算法步骤

当网络训练完成后，即可利用训练好的Q网络对迁徙参数进行调整优化，并在优化完成后继续执行遗传迭代，直到获得最终的Pareto 最优解集结果。该部分的算法步骤如表4所示。

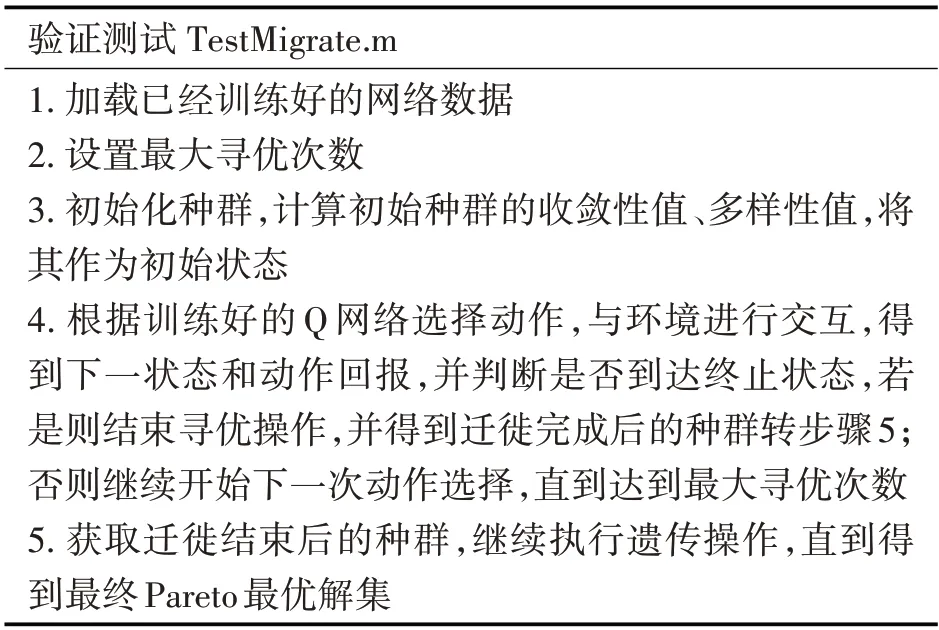
表4 验证测试算法步骤

4 仿真实验

4.1 想定设计

假设某一时刻，我方决定对敌方舰艇编队发起攻击。初始状态下，我方共有4 种不同类型的反舰导弹，敌舰编队共有5 艘舰船目标，一些参数信息详见表5～表8，数据来源参考文献［15］。规定整个过程中分给各目标的弹量总上限均为12 枚，避免造成弹药浪费。算法遗传迭代终止后输出武器目标分配方案，作为一个打击波次。每波次打击结束后评估各目标的毁伤程度，确定剩余弹量，根据战场信息并结合表8 确定是否继续解算下一波次方案，规定对所有目标的毁伤程度应为重伤或击沉。

表5 目标威胁程度

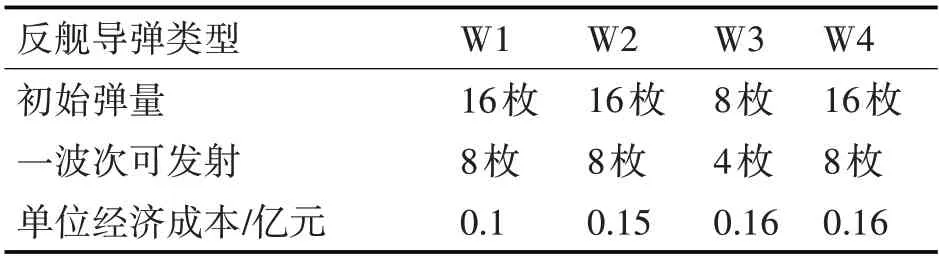
表6 反舰导弹基本信息

表7 导弹对目标毁伤概率

表8 毁伤程度区间

4.2 实验结果与分析

设置对比实验来验证本文基于深度强化学习的改进NSGA-II 算法在求解WTA 问题上的有效性，选择传统单种群NSGA-II 算法、普通双种群NSGA-II算法（迁徙参数按照人类经验设置）、与本文方法进行对比，比较最终生成的Pareto 解集的收敛性、多样性、算法耗时长短等。

1）收敛性、多样性对比

将上述三种算法的程序各自独立运行20 次，记录每一次运行后最终种群的收敛性值、多样性值，对20 次的结果取平均，结果如表9 所示。由表可知，对比传统单种群NSGA-II 算法，本文的改进算法结果在收敛性和多样性上均有一定程度的提升。进一步对比普通双种群NSGA-II 算法和本文方法，可以看出本文所提出的基于DQN 的改进NS⁃GA-II 算法在收敛性和多样性上与对比算法表现基本一致。

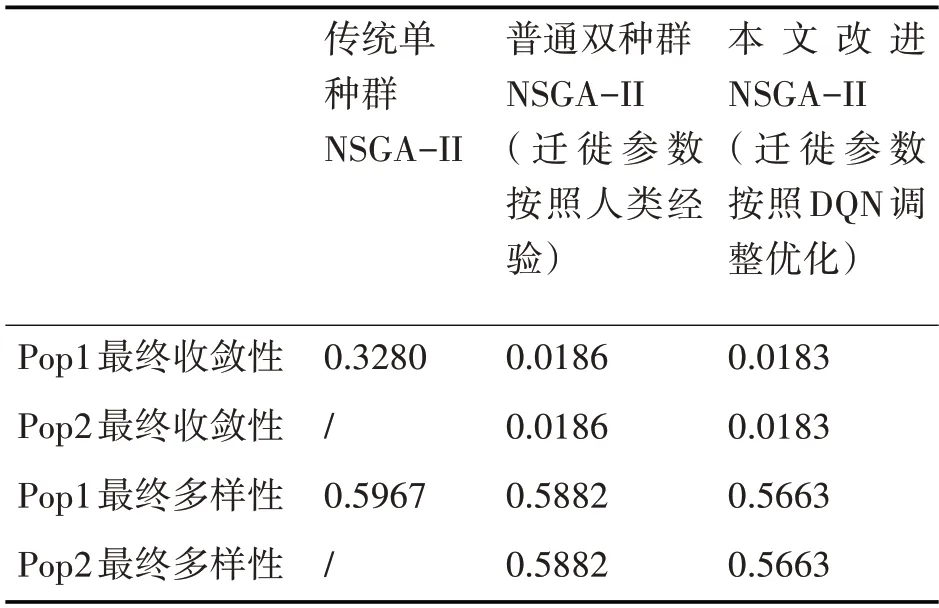
表9 算法收敛性与多样性对比

2）算法运行耗时对比

记录三种算法生成最终Pareto 前沿的运行时间，将20 次运行耗时取平均值，结果如表10 所示。由表10 可知，与其他两种算法进行对比，尽管本文基于深度强化学习的改进NSGA-II 算法前期需要较久的时间用于模型的训练，但在最后的优化阶段耗时较少，表现更佳。

表10 算法运行耗时

3）优化目标函数值对比

将三种算法的程序各自独立运行20 次，记录每次最终Pareto前沿结果中目标函数f1的最大值、f2的最小值，绘制两个目标函数的20 次结果的统计箱线图如图2、图3 所示，从图可以看出，传统单种群NSGA-II 算法在两个目标函数上的数据均存在较大的波动，表明该方法的解集结果随机性较大，不够稳定；双种群NSGA-II 算法和本文方法均引入了迁徙思想，可在传统单种群NSGA-II算法基础上改善不稳定的问题；对双种群NSGA-II算法和本文方法做进一步对比可知，本文方法将深度强化学习DQN 用于迁徙参数的优化，尽管可以在算法性能和算法耗时上获得一定的改善，但算法在鲁棒性上略显不足。

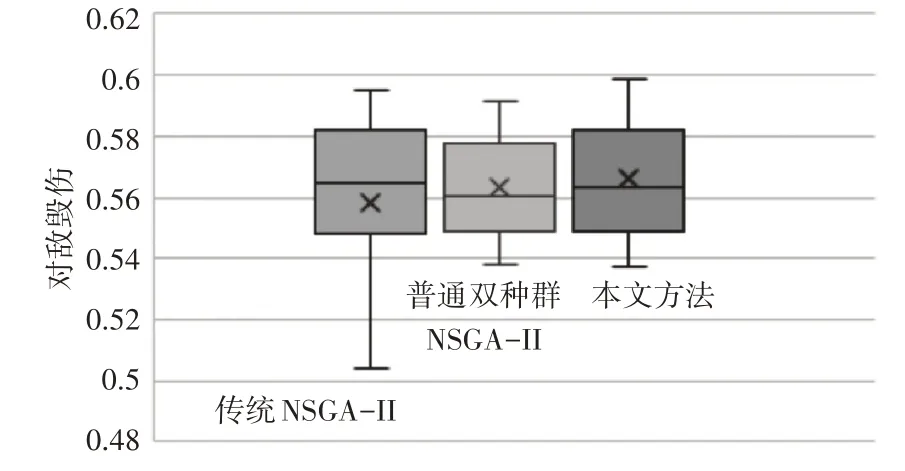
图2 不同算法对敌毁伤箱型图

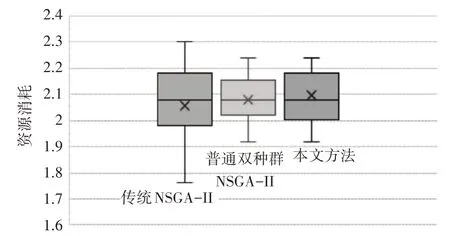
图3 不同算法资源消耗箱型图

5 结语

本文针对传统单种群NSGA-II 算法在求解WTA 数学模型时，容易陷入局部最优、多样性不足等缺陷，提出可引入深度强化学习和双种群“迁徙”思想对其进行改进，利用深度强化学习DQN 算法来对“迁徙”操作涉及到的三项参数进行优化。面向具体的海战场武器目标分配场景进行仿真实验，结果显示：与传统单种群NSGA-II 算法、迁徙参数依靠人类经验进行设置的普通双种群NSGA-II 算法相比，本文所提出的基于深度强化学习的改进NSGA-II 算法可以获得更好的收敛性、多样性结果，且算法耗时更少，验证了本文改进方法的有效性。