土力学中饱和土渗流固结理论的教学方法研究

徐令宇 张杰 陈炜昀 高洪梅

摘  要：Terzaghi饱和土单向固结理论的提出标志着土力学成为一门独立学科，土的渗透及固结是土力学教学的重点，同时也是教学难点。为使学生更为形象掌握和理解该知识点，该文提出一种数学方程与数值模型相结合的教学方法，从Biot渗透固结理论的偏微分方程出发，在通用有限元软件中建立并验证数值计算模型。通过渗流固结方程的介绍和说明，理解“渗流”和“固结”的过程及区别和联系。基于数值结果，形象说明达西定律中“水头”的概念。

关键词：土力学；饱和土渗流固结理论；教学方法；数值计算；有限元

中图分类号：G642        文献标志码：A          文章编号：2096-000X（2023）21-0083-04

Abstract： The emergence of Terzaghi seepage consolidation theory in Soil Mechanicsmarks that Soil Mechanics has become an independent subject. In order to make students grasp and understand the theory more vividly， this paper initially presents partial differential equations （PDEs） of the theory， and then proposes a numerical calculation model based on general finite element software.This paper introduces and explains the seepage consolidation equation， let students understand the process of "seepage" and "consolidation" and the difference and connection. At the same time， based on the numerical results， the concept of "water head" in Darcy's law is illustrated.

Keywords： Soil Mechanics; seepage consolidation theory of saturated soil; teaching method; numerical calculation; finite element

Terzaghi飽和土单向固结理论的提出标志着土力学成为一门独立学科，是岩土工程问题研究的基础，该知识点是土力学教学的重点，也是教学难点[1]。为了让学生更容易掌握该知识难点，已有文献探讨了多种土力学教学方法或者教学模式。伊盼盼[2]建议采用内化式教学模式，目标是让学生意识到自己处于教学中的主体。杨兵等[3-4]建议以实例带动理论教学，激发学生学习兴趣，进一步建议增加观看、分析失败的工程案例，让学生意识到理论重要性，同时通过对土力学试验方案创新设计也能够激发学生的学习热情。在疫情形势下，加瑞等[5]利用在线课程资源，开展基于“互联网+”的线上线下混合式教学改革，同时建议充分利用国家虚拟仿真实验教学项目共享平台上的虚拟仿真实验开展线上实验教学。综上可以看出，目前土力学教学主要集中于宏观方法的研究，较少涉及对土力学中重难点问题提出实操性方法。

本文针对土的渗透固结理论这一重要知识点，提出一种数学方程与数值模型相结合的教学方法，让学生学会求解土力学中的数学方程，从理论角度理解实际工程问题。通过渗流固结方程的介绍和说明，理解“渗流”和“固结”的过程、区别和联系。基于数值结果，形象说明了达西定律中“水头”的概念。通过本文的讲解，将土力学中的有效应力原理、达西定律、固结理论有机的串联起来，有助于提高学生学习兴趣和学习效率。

一  渗流固结控制方程

Biot[6]提出了经典的饱和土的渗流固结方程，将土的变形与土的渗流耦合在一起。本文将以二维固结为例，详细介绍了其微分控制方程，并在COMSOL Multiphysics软件建立数值模型，将模型退化为一维情形，将计算结果与Terzaghi饱和土单向固结方程解析解进行了对比。

（一）  固相控制方程

公式（1）和公式（2）分别给出了固相在水平向和竖向力的平衡方程，该方程引入了有效应力原理：总应力为有效应力和孔压之和，即隐含了土体为完全饱和的假定。因此，σx和σz分别为水平向和竖向有效应力，p为孔隙水压力。竖向力的平衡方程考虑了自重作用，ρ为饱和土的密度，g为重力加速度，τxz为剪应力。

（1）

（2）

假定土层为均质、各向同性的弹性体，通过引入弹性本构方程，应力和应变的表达式写为

（3）

式中：εx、εz和γxz分别为x方向正应变、z方向正应变及工程剪应变。K和G分别为体积模量和剪切模量，可写成弹性模量和泊松比的表达式

应变可通过位移求出，定义为

（6）

式中：u和w分别为x和z方向的位移。

（二）  液相控制方程

地下水渗流的驱动力是水头差，压力水头H定义为

（7）

式中：γw为水的重度；p/γw代表压力水头。

根据流体连续性条件，假定土颗粒和水是不可压缩的，可得到渗透速度与体应变εv的关系式

（8）

式中：vx和vz分別为x方向和z方向的渗透速度，t为时间。

根据线弹性理论，εv的表达式为

（9）

根据达西定律，渗透速度表示为

（10）

式中：kx和kz分别为x方向和z方向渗透系数。把式（9）和式（10）带入到公式（8）中，可以得到

若令式（11）右侧为零，即不考虑土体变形，方程退化为著名的拉普拉斯方程，也就是土力学教材中提到的平面渗流的控制方程。结合边界条件，即可联合求解式（1）、式（2）、式（11），得到u、w及p。这些边界包括已知水头边界和法向流速边界。下面结合Terzaghi饱和土单向固结求解来说明。

（三）  Terzaghi饱和土单向固结算例

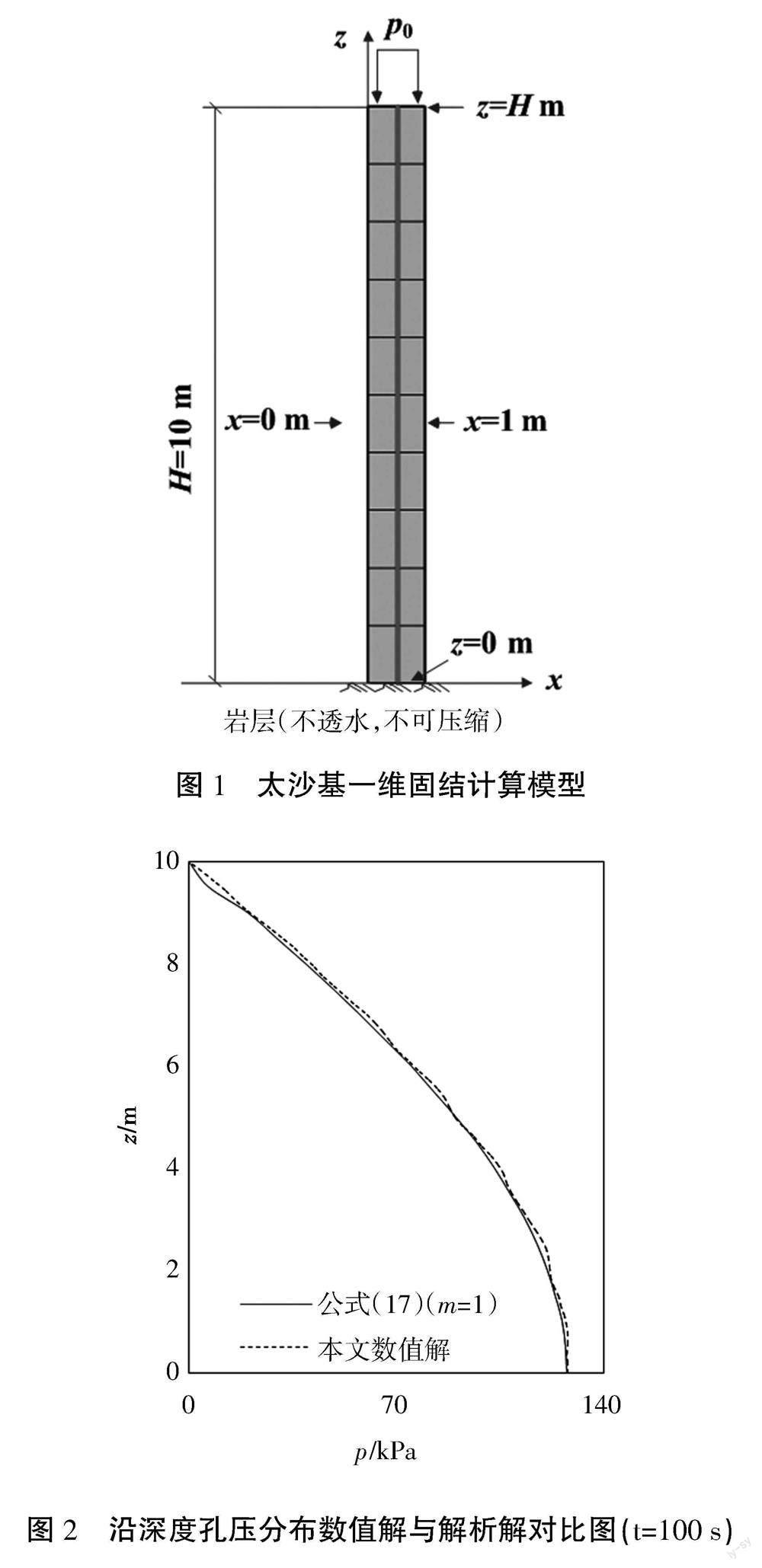
本文首先在COMSOL Multiphysics软件建立Terzaghi饱和土单向固结方程数值模型，模型土如图1所示。Terzaghi饱和土单向固结理论为一维情形，在有限元软件中仅设置竖向渗流，公式（11）退化为

（12）

通过添加固体力学和一般形式偏微分方程两个物理场，将土的变形与土的渗流耦合在一起。需要同设置边界条件，来满足偏微分方程的求解，具体为：①设置模型顶面单面排水（公式（13））；②模型两侧不透水且水平位移为零（公式（14））；③模型底部不透水且约束水平位移和竖向位移（公式（15））。初始条件为公式（16），施加的均布荷载为p0=100 kPa。

p=0，z=H ，                （13）

p=p0，t=0 ， （16）

式中：l为土柱模型宽度；H为土柱模型深度。根据上述渗流固结方程、边界条件及初始条件，文献[7]给出了土层任意深度z不同时刻t的孔隙水压力解析解

式中：m为正奇数，Cv为土的固结系数；Tv为无因次的时间因数；Es为压缩模量；p0为土柱顶部施加的压力。

假设一维固结模型尺寸宽度l为1 m，深度H为10 m的长方形土柱，土体密度ρ为1.72×103 kg/m3，渗透系数k为1.75×10-7 m/s，泊松比v为0.3，压缩模量Es为3.4 MPa。图2给出了t=100 s时刻孔隙水压力分布图，可以看到，数值解和解析解基本吻合，验证了数值模型的正确性。

二  二维渗流算例与结果分析

下面将利用上述数值模型计算一个二维渗流算例，计算模型及网格如图3所示。土体模型尺寸长l=50 m，深H=40 m，模型中间有一个不透水挡墙，挡墙宽2 m，插入深度为19 m，挡墙上游水头H1=10 m，挡墙下游水头H2=2 m。计算的土体参数与“Terzaghi饱和土单向固结算例”小节相同。

在有限元计算中，仅考虑渗流场，因此固体边界全部约束（即u=w=0），仅考虑流体边界，计算模型两侧及底部采用不透水边界（即          ），上下游边界为已知水头边界。

上游水头边界条件

p=ρwgH1，z=H 。        （19）

下游水头边界条件

p=ρwgH2，z=H ，            （20）

式中：ρw为水的密度，g为重力加速度。

图4给出了有限元计算出的等势线和流线，同时给出每个等势线的水头值。可以看出以下几点。

1）AB和GH分别为首位两条等势线，对应公式（19）和公式（20）所示的边界处水头。

2）BCEFG和AJIKH为不透水边界，是两条边界处的流线，所有等势线均匀流线垂直。

3）由于计算模型为对称模型，EI等势线值为6 m，是首尾等势线的均值。

三  结论

本文针对土的渗透固结理论这一重要知识点，提出一种数学方程与数值模型相结合的教学方法。通过土的渗流固结偏微分方程介绍，理解“渗流”和“固结”的过程及区别和联系。在通用有限元软件中建立数值模型，并利用Terzaghi饱和土单向固结解析解进行了验证。通过二维渗流算例，形象说明了达西定律中“水头”的概念。本文将土力学中的有效应力原理、达西定律、固结理论有机的串联起来，有助于提高学生学习兴趣和学习效率。

参考文献：

[1] 赵成刚，李舰，宋朝阳，等.土力学理论需要发展与变革[J].岩土工程学报，2018，40（8）：1383-1394.

[2] 伊盼盼.开发内化教学方法在《土力学》中的应用[J].当代教育实践与教学研究，2015（11）：211.

[3] 杨兵，苟锦程，侯江荣.新时期土力学教学方法探索[J].教育现代化，2019，6（89）：33-34.

[4] 杨兵，侯江荣.土力学课程教学现状及教学方法思考[J].教育教学论坛，2020（11）：219-220.

[5] 加瑞，雷华阳，刘景锦，等.土力学课堂和实验教学改革的探索与实践[J].高等建筑教育，2021，30（6）：39-46.

[6] BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics，1941（12）： 155-164.

[7] 赵明华.土力学与基础工程[M].武汉：武汉理工大学出版社，2014.