数字孪生基础数据底板DEM修正方法研究
2023-08-02洪明海王兴建汪仕伟魏文杰李析男冯楚桥
洪明海,严 涛,刘 辉,王兴建,敬 娜,汪仕伟,魏文杰,李析男,冯楚桥
(贵州省水利水电勘测设计研究院有限公司,贵州 贵阳 550002)
为全面推进算据、算法、算力建设,加快构建具有“四预”(预报、预警、预演、预案)功能的智慧水利体系,水利部发布的《“十四五”智慧水利建设实施方案》《数字孪生流域建设技术大纲(试行)》《数字孪生水利工程建设技术导则(试行)》《水利业务“四预”功能基本技术要求(试行)》等指导文件和技术要求[1],明确提出数据底板是数字孪生流域建设的重点任务之一,数字高程模型(DEM)则是数据底板中最重要的数据之一。
DEM于1958年由国外提出,基于DEM的数字地形分析在遥感测绘[2]、资源调查、环境保护、工程建设、灾害防治、水利规划设计[3]以及地学研究等各方面都展现出越来越重要的作用。通常,DEM主要来源于摄影测量、已有地形图数字化、已有的DEM库中提取、地面测量等。通过地面测量的等高线生成DEM不仅精度可控,操作方便,而且现有技术相对成熟稳定,是工程实践中最常用的DEM获取方式之一。然而,当研究区域较大(如一个地级市或者一个省)且等高线为大比例尺(万分之一或者五千分之一甚至更大)时,常常会因为电脑等硬件设施的限制使得DEM的获取不能一次性完成,需要分幅生成后再镶嵌,这样在分幅之间的缝隙往往就会产生误差甚至是Nodata值,给工程应用带来不小的困扰。
目前对于DEM修复的方法主要有3种:一是利用局部修正后进行反距离加权融合填补[4];二是建立误差分布模型来判断系统误差等指标后采用自适应平滑[5]、智能滤波[6]等对DEM噪音进行修复;三是以别的DEM来做参考校正缺失的区域[7]。事实上,DEM数据集的误差分布与土地利用类型、坡度、坡向、高程地形、地表植被类型等有关[8],也就是缺失的像元高程值与周边的像元是有关系的。当处理大面积大批量的DEM修复时,高效快速且精度可控的方法显得尤为重要[9]。
本文拟采用ESRI公司的ArcGIS软件,通过万分之一等高线来获取某市DEM,同时通过Python对生成的DEM分幅处进行适当的修正,将修正的结果和已有的数据进行比较分析,为大范围大尺度的等高线生成DEM提供一种借鉴方法。
1 材料与方法
1.1 研究区概况和数据来源
本次研究的区域位于贵州省某市某局部区域,研究区面积约为57 km2,海拔高度为935~1 345 m,境内地形起伏大,地貌类型较为复杂。
本文使用的研究数据为测量部门提供的1∶10 000的等高线和高程点数据,为shp格式,坐标系为CGCS2000投影坐标,其中等高线共4 716段,高程点共415个;对比的DEM为自然资源部门提供的同一区域数据,GDB格式,CGCS2000投影坐标。
1.2 计算原理
等高线生产DEM[10],主要涉及等高线/高程点转TIN,然后由TIN生成DEM,对DEM进行镶嵌后再修正。
不管是地形转TIN还是TIN转DEM工具,都是一个占用大量内存的应用程序,因此不能创建较大的输出栅格。按照ArcGIS官方(https://resources.arcgis.com/zh-cn/help/main/)给出的处理方案“创建多个DEM后,最好使用镶嵌地理处理工具的BLEND选项或MEAN选项将它们合并”。因此在处理全市乃至全省上万副大比例尺的等高线生成DEM后最终需要将它们拼接起来[11-12],然后对分幅的缝隙采用MEAN方法修正。
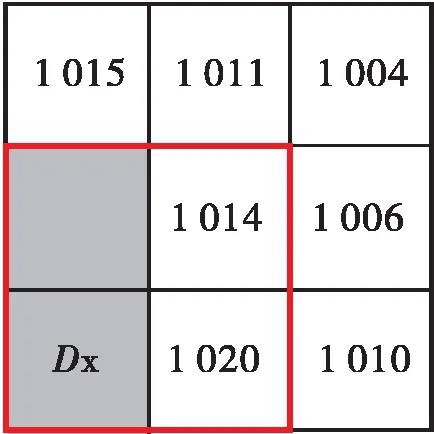
从概念上讲,该修正方法会将要修正的像元或中心像元周围一个3×3的像元邻域的高程值参与计算。图1所示,如果邻域内某个像元位置的高程值为NoData,则将中心像元周边8个有值像元值的平均值指定给该位置,计算见式(1):

a)像元位置
(1)
式中Dx——待修正的DEM像元;Di——周边8个像元有值的栅格像元值;n——周边8个像元中有值的个数,最大取8。
例如图1a中NoData的Dx,当其周边的8个像元值都不为NoData时,
Dx=(D1+D2+D3+D4+D5+D6+D7+D8)/8
(2)
当NoData的Dx周边的8个像元值均为NoData时,则该像元值赋值也为NoData。
当修正像元周边未读取到3×3的像元邻域或者读取到的3×3的像元邻域中的8个像元中可能会有多个NoData时,则参与计算的周边像元数是不为NoData的个数,见图2。图2a、2b、2c为周边邻域为2×2的像元,且3个像元值分别有1个、2个、3个NoData的像元,当2×2的邻域像元中有3个NoData时,则待修正的像元栅格也为NoData,见图2c。此外,当处理DEM边界时,还可能读取到2×3的像元或3×2的像元,见图2d、2e;其处理方法同上。或者读取到3×3的像元邻域中有多个NoData(图2f),则参与计算的为有值部分。
a)1个像元无值
1.3 研究技术路线及步骤
本文的研究技术路线见图3,其主要操作步骤如下。
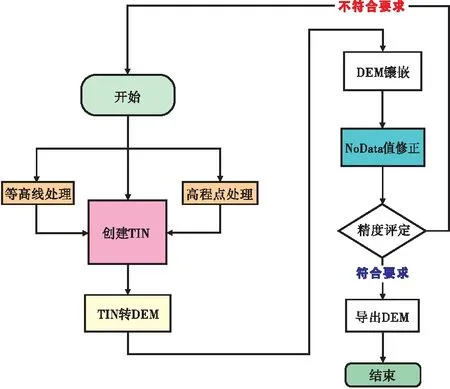
图3 研究技术路线
步骤一对研究区范围内的等高线和高程点数据处理。将CAD格式的地形图分别转为等高线shp和高程点shp,并定义正确的投影坐标系后,对等高线和高程点数据中高程值为0、无高程值、高程值异常的数据进行细部识别并处理(删除或重新赋值)为正常值,然后去除等高线或高程点重合的要素。
步骤二将处理好的等高线和高程点数据作为创建TIN的输入数据,其中等高线要素作为contour,高程点要素作为masspoint。
步骤三使用前文生成的TIN转DEM,根据输入地形图的比例尺设置合适的容差和像元大小。
步骤四重复步骤一、二完成所有单幅地形图转为DEM后将所有DEM进行镶嵌。
步骤五对镶嵌后DEM进行NoData值修正处理。
步骤六对修正后的DEM进行精度评定,符合要求则导出DEM,不符合则回到地形图的处理重新设置像元大小、容差等。
1.4 分析指标及评定标准
常用的高程评定[13]方法有检查点法[14-15]、剖面法、分形法、影像分析法、等高线回放法[16-17]等,本文采用中国国家标准化管理委员会发布的GB/T 18316—2001《数字测绘产品检查验收规定和质量评定》[14]中的检查点法进行分析,即对生成的DEM采用修正方法修正后NoData像元值和已知的DEM值进行比较,计算中误差。中误差按照GB 50026—2020《工程测量标准》[18]5.9.6计算,见式(3):
(3)
式中m——数字高程模型(DEM)高程中误差;n——检测点数,按照GB/T 18316—2008《数字测绘成果质量检查与验收》[15],要求检测点分布均匀,位置易于辨认,不少于50个;Ri——检测点的修正高程值;Zi——检测点的原始高程值。
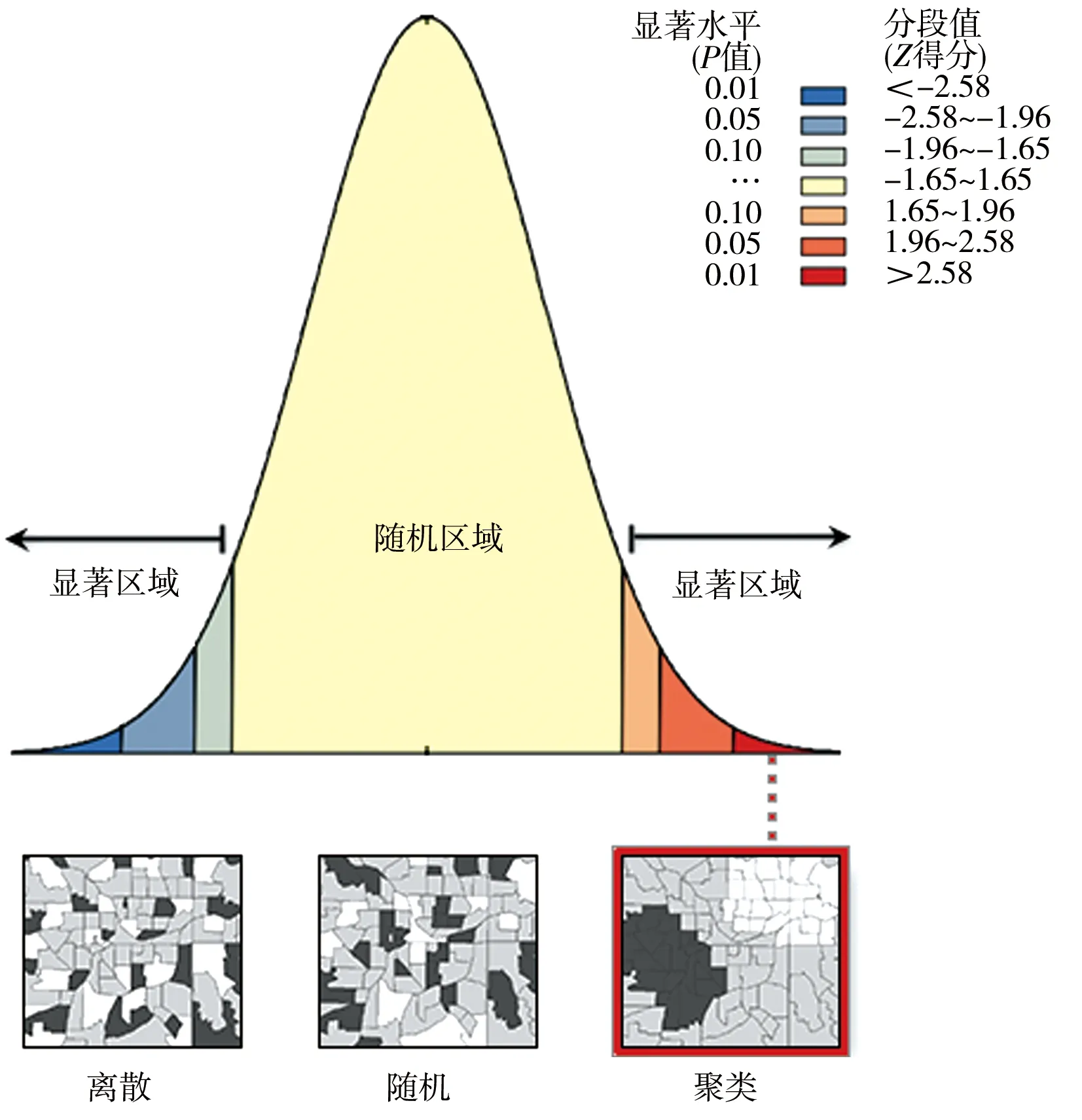
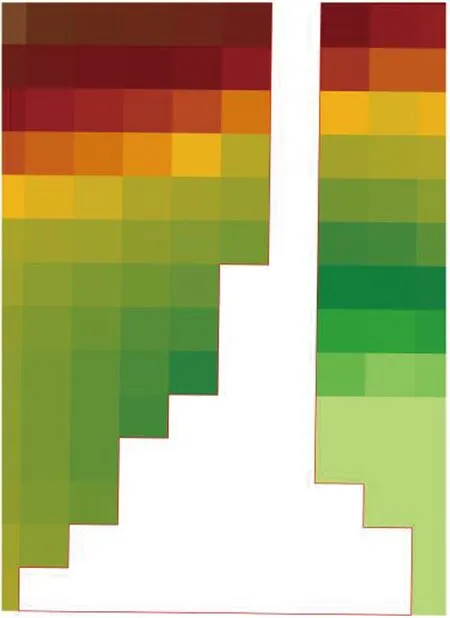
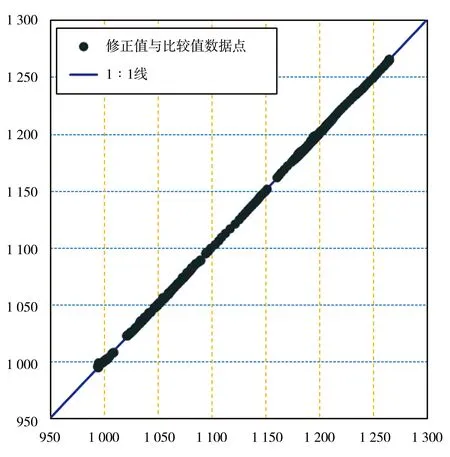
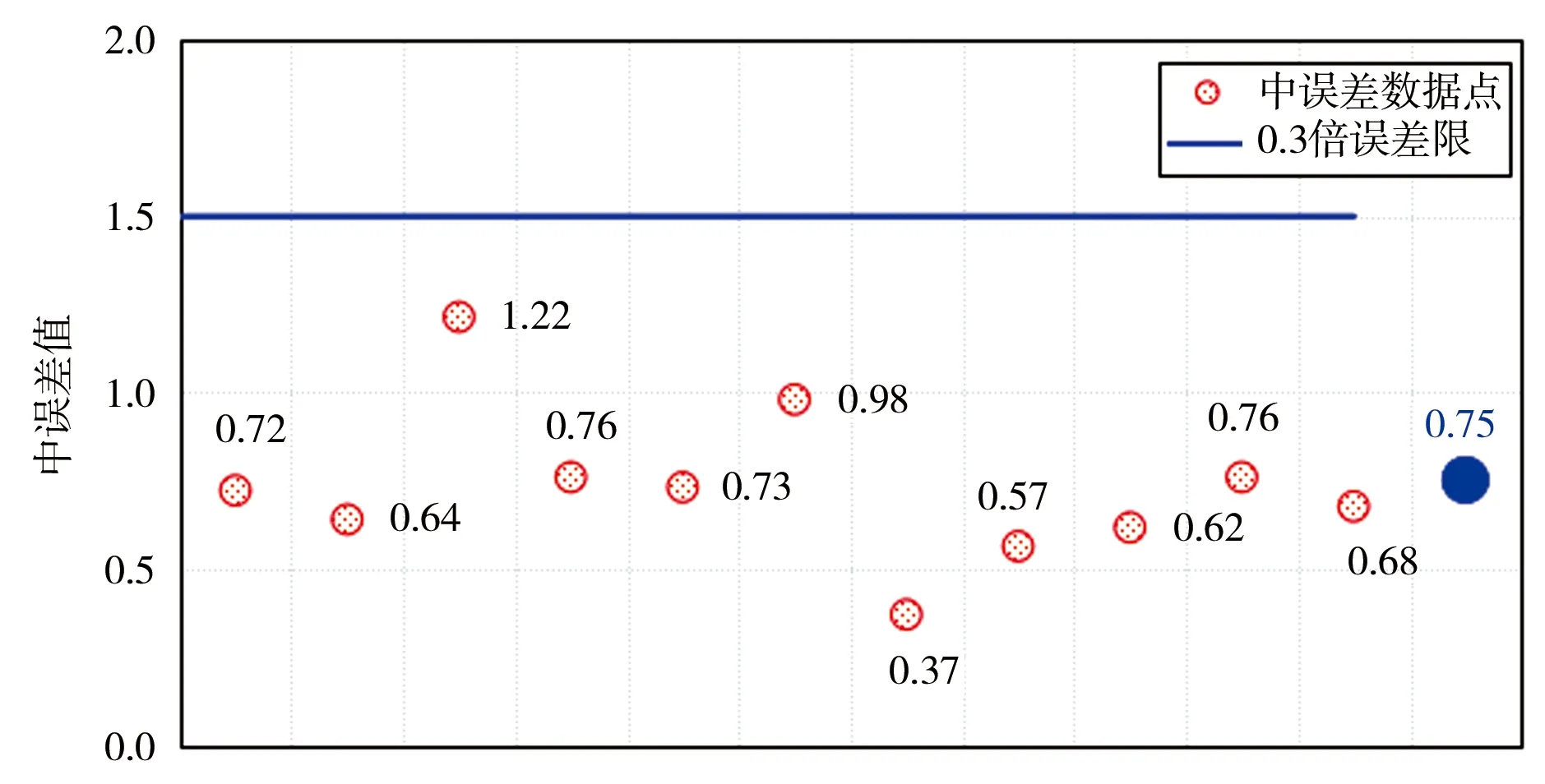
当m 参照GB 50026—2020《工程测量标准》条文说明5.1.3中,地形图的基本等高距,是以等高线的高程中误差的经验公式验算,数字高程模型格网间距的选取及格网点高程中误差应符合表1的规定。 表1 数字高程模型格网间距的选取及格网点高程中误差 单位:m 参照5.9.6条数字高程模型建立后应进行检查,并应符合下列条件:对于实测数据所建立的数字高程模型,应进行外业实测检查并统计精度。每个图幅的检查点数,不应少于20点,检查点与模型插值点的高程较差不应大于本标准第5.1.7条相应格网点高程中误差的2倍。等高线高程中误差mb的取值,对于常用的设计坡度,均不能大于基本等高距的1/2;对于较大的设计坡段,也不能大于基本等高距。 此外,参照DL/T 5001—2014《火力发电厂工程测量技术规程》[19]中第6.1.4条等高线插值点或相对与临近图根点的高程中误差的规定,见表2。 表2 等高线插值求点的高程中误差 单位:m 综上,本研究区地形类别为山地和高山地,为1∶10 000比例尺,数字高程模型的插值点高程中误差限值m0取1倍基本等高距(格网尺寸),为5 m。 地理学第一定律指出,任何事物都是与其他事物相关的,相近的事物关联更紧密[20],空间自相关分析对具有地理坐标的要素进行相关程度表征[21],即空间分布模式(spatial distribution pattern),一般有聚集、离散和随机3种模式,而空间自相关中用来表征空间分布模式的量化指数一般使用莫兰指数[22]。DEM是典型的具有坐标信息的要素,其高程值常常和地形的变化存在很大的联系,即空间相关性。 图4是比较值DEM转换为高程像元方格后做的空间自相关分析结果,参与计算的78 018个单元值(一般莫兰指数分析样本大于30个即可)表明DEM的高程分布存在空间上的高度聚集(图4 Clustered)。分析结果数据见表3,其中莫兰指数为0.999 796,莫兰指数代表数据的相关程度,其值范围为[-1,1],本次自相关分析表明高程值和位置关系相关性非常大,即高值与高值发生聚集,低值与低值聚集,空间上呈现正相关模式;表3中的Z得分和p值则代表分析的置信度,当Z>2.58且p<0.01时其置信度为99%,本次分析结果Z得分为393.212 387 369,则随机产生此聚类模式的可能性小于1%,因此高程值和地理位置是高度自相关的,这也印证了ArcGIS官方推荐的镶嵌DEM栅格时为处理接幅的缝隙采用“BLEND”或者“MEAN”方法是适宜的,也即是表明本文对NoData采用周边9个有值像元修正的方法是合适的。 表3 空间自相关分析结果数据 图4 比较值DEM空间自相关分析图莫兰指数 图5是接幅缝隙DEM的NoData值修正前后的局部截图比较,其中图5a为修正前,其接幅处存在空白的NoData值,会影响DEM的后续数据分析,比如集雨面积量算;图5b是修正后的像元,图5c是比较值的像元,可以看到采用本文提出的方法修正的像元高程值和比较值的差异非常小,图5中展示的39个像元值中37个的修正值和比较值相差均在1 m以内,远远低于规范规定的误差限5 m和采样间距5 m,最大值也仅为1.11 m,也满足规范要求的误差限值。 a)NoData像元空值 图6是本次研究区域内接幅缝隙中306个NoData像元的修正值和比较值的点绘图,可以看出,306对数据几乎均匀分布在1∶1线附近,表明采用本文提出的方法修正的DEM高程值和真值(比较值)非常接近,数据计算结果也表明修正值和比较值的最大差值仅为3.55 m(图7),也低于规范规定的误差限5 m和采样间距5 m。 图6 修正值与比较值数据点比较 图7 修正值与比较值高程差 将研究区域306个NoData像元的修正值和比较值按照各自所在的空间位置关系,自然形成11组,分别计算中误差,结果见图8,中误差不等于真误差,它仅是一组真误差的代表值。中误差的大小反映了该组观测值精度的高低,因此,通常称中误差为观测值的中误差。其中,中误差最大值为1.22,是第三组,最小值是第7组的0.37。此外,还可以看出11组的中误差值和总体的中误差值0.75都在0.3倍误差限的下方,低于规范要求的中误差限值。 图8 中误差分布 按照GB/T 18316—2008《数字测绘成果质量检查与验收》[15],当成果质量符合要求后还可以计算质量元素分值S,并对单位成果质量进行等级评定。计算见式(4): (4) 式中S——质量元素分值,其分值对应的等级分类见表4;m0——允许中误差值,参照表1取值;m——数字高程模型(DEM)高程中误差,按式(3)计算。 表4 单位成果质量评定等级 根据GB/T 18316—2008《数字测绘成果质量检查与验收》规范,采用本方法修正的研究区域的DEM高程值的中误差均小于0.3倍中误差,其质量元素分值S为100分,按照表4的等级评定结果为优级品。 本文通过Python调用ArcGIS相应的工具来批量修正某市某研究区域的地形转DEM后接缝处存在的高程NoData值,其主要结论如下。 a)方法适用性强。参与计算的78 018个单元值的自相关分析表明DEM的高程值存在高度的自相关性,空间分布模式结果为聚类,其中莫兰指数为0.999 796,Z得分为393.212 387 369且p小于0.1,则随机产生此聚类模式的可能性小于1%。此外ESRI官方推荐的镶嵌DEM栅格时为处理接幅的缝隙采用“BLEND”或者“MEAN”方法。因此本文提出DEM的NoData值采用周边8个有值像元的均值来修正的方法是可行的。 b)修正结果可靠。局部计算39个像元值中37个的修正值和比较值相差均在1 m以内,最大值也仅为1.11 m;本次研究区域内接幅缝隙中306个NoData像元的修正值和比较值的数据几乎均匀分布在1∶1线附近,修正值和比较值的最大差值仅为3.55 m,低于规范规定的误差限5 m和采样间距5 m。11组中误差最大值为1.22,最小值是0.37,且总体的中误差值0.75都在0.3倍误差限内,低于规范要求的中误差限值,其质量元素分值S为100分,评定结果为优级品。 c)计算速度快,节约时间成本。从栅格计算的原理出发,采用Python调用ArcGIS将处理图像问题转化为矩阵运算问题,而矩阵运算速度极快则是Numpy最大的优势,本研究区域的修正计算用时仅为10 s(ArcGIS暂时没有直接的修正工具,采用镶嵌栅格也不一定能覆盖所有的接缝处NoData值)。此外,本方法还可以批量处理,通过矩阵分块快速完成任务,不存在内存限制处理失败等情形,这些都是ArcGIS无法比拟的,生产实践中可极大地提高工作效率,为DEM后续的计算分析奠定基础。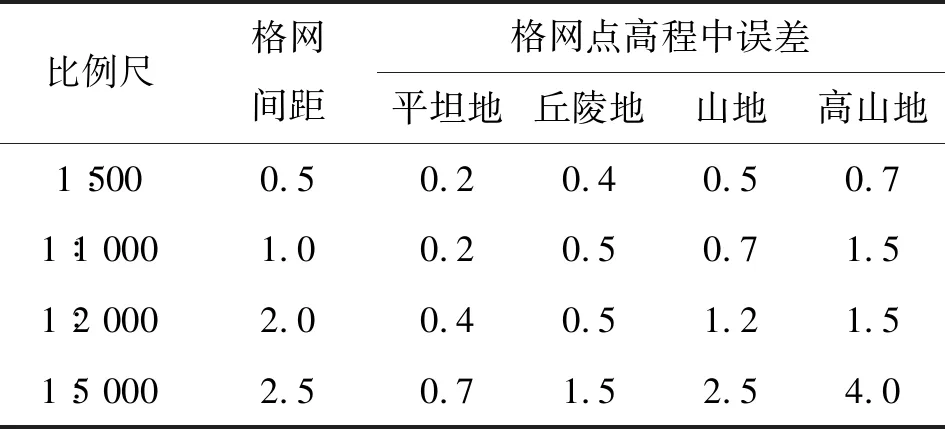

2 结果与讨论
2.1 修正方法的适用性

2.2 修正结果

2.3 中误差分析
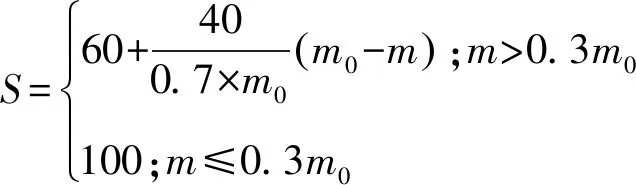

3 结论
