表面形貌对单晶CoCrFeMnNi高熵合金刮擦行为影响的分子动力学模拟

2023-08-01罗灵芝

摩擦学学报 2023年7期

王冰,罗灵芝,古斌

(西南科技大学制造科学与工程学院制造过程测试技术教育部重点实验室,四川绵阳 621010)

自Yeh等[1]和Cantor等[2]分别独立地报道了等原子比或近等原子比的具有多种元素组成的高熵合金以来，高熵合金的变形行为引起国内外学者的广泛关注[3-8]. CoCrFeMnNi高熵合金作为1种新型工程材料因其优异的力学性能而使得其在微纳机电系统中具有巨大的应用潜力[1-3]. CoCrFeMnNi高熵合金器件在服役过程中会不可避免地承受刮擦载荷的作用，产生刮痕或者磨损. 为了提高纳米高熵合金器件的装配精度和服役可靠性，需要对CoCrFeMnNi高熵合金的刮擦变形行为进行深入研究.

对CoCrFeMnNi高熵合金变形行为的早期研究主要关注拉伸或压缩载荷作用下的变形行为和变形机理，目前已通过试验研究揭示了加载率、环境温度和晶粒尺寸等因素的影响. 例如，Park等[9]指出准静态加载下率依赖性的本质是由非弹性变形过程中内部热效应引起的温度变化造成的，然而冲击载荷作用下率依赖性的本质是由温度变化和黏性对位错运动的影响共同决定的；Gludovatz等[10]和Aitken等[6]讨论了低温下孪晶对CoCrFeMnNi高熵合金位错运动的阻碍作用和该合金的应力-应变响应曲线对温度的依赖性；Ji等[11]的试验结果表明12.70 nm晶粒尺寸的CoCrFe-MnNi高熵合金在室温下展现出1.99 GPa的高抗压强度. 除试验外，分子动力学(Molecular dynamics,MD)模拟也已应用于分析CoCrFeMnNi高熵合金在拉伸或压缩载荷作用下的变形行为和微结构演化机理，并取得了一定研究成果[12-13]. Choi等[14]发现CoCrFeMnNi高熵合金中孪晶沿着不全位错面形成，并且高熵合金中严重的晶格扭曲会促进位错的形成. Fang等[15]揭示双相CoCrFeMnNi高熵合金中应变诱发相变可以进一步提高纳米多晶高熵合金的延展性和断裂强度. 胡远啸等[16]讨论了纳米尺度下CoCrFeMnNi高熵合金力学行为的温度效应和强韧机理. Qi等[17-19]通过分子动力学模拟研究了纳米多晶CoCrFeMnNi高熵合金的温度和加载率依赖性及晶向依赖性.

当高熵合金受到压痕和划痕/刮擦载荷作用时，Nagarjuna等[20]通过试验分析指出，由滑动摩擦引起的晶粒细化会引起等原子比的CoCrFeMnNi高熵合金变形层的硬度增加. 在数值模拟研究方面，Tang和Li[21]研究了CoCrFeMnNi和CrFeCoNi高熵合金在单向和双向划痕载荷下的纳米摩擦机理. Qi等[22]通过分子动力学模拟研究了纳米多晶CoCrFeMnNi高熵合金在刮擦载荷作用下的力学行为和微结构演化.

在实际应用中，高熵合金表面存在微纳尺度的表面粗糙度，并具有不同的表面形貌. Li等[23]揭示出单晶铜的刮擦切向力和摩擦系数呈现出强烈的表面形貌依赖性，并且精密加工过程中的切削质量可以通过对表面形貌的调控来实现. Qi等[18,22]进一步指出随着孪晶界距离的减小，刮擦过程中形成的不全位错会显著影响CoCrFeMnNi高熵合金的非弹性变形，这表明表面形貌会影响CoCrFeMnNi高熵合金的刮擦行为.尽管CoCrFeMnNi高熵合金在纳米刮擦中的微观变形行为已得到初步的研究，但表面形貌对CoCrFeMnNi高熵合金刮擦行为的影响尚未见研究报道. 因此，本研究中利用MD模拟方法研究在纳米刮擦载荷作用下，表面纹理形貌和刮头半径对CoCrFeMnNi高熵合金的刮擦响应和微结构演化的影响.

1 模拟方法

图1所示为模拟单晶等原子比CoCrFeMnNi高熵合金刮擦行为的MD模型示意图. CoCrFeMnNi高熵合金是面心立方晶格(Face Center Cubic,FCC)结构. 如图1所示，模型由高熵合金试样和金刚石刮头组成，其中高熵合金试样分为牛顿层、恒温层和固定层. 模型中X、Y和Z方向分别对应晶向[100]、[010]和[001]，CoCrFeMnNi高熵合金的初始晶格常数为3.59 Å[14,24]，高熵合金在X，Y和Z方向的尺寸分别是11.2、6.0和3.2 nm，恒温层和固定层的厚度均为0.4 nm. 刮头半径设为1.2 nm. 研究中考虑图2所示的3种高熵合金表面形貌：平面(A1)、矩形(A2)和三角形(A3)，其中，矩形和三角形表面形貌的高度、宽度或底边边长和间距都是0.8 nm.平面、矩形和三角形表面形貌的划痕深度均是从织构最高点开始计算. 模拟晶胞在Y方向采用周期性边界条件，在X和Z方向采用自由边界条件. 刮头半径分别设置为0.6、1.2和1.8 nm，划痕方向的边界为周期性边界条件，在此边界条件下，模拟中不会出现边界不足以抑制划痕的情况.

在刮擦模拟前，模型在恒温恒压的环境下进行驰豫以使原子达到平衡状态. 在弛豫过程中，试样与刮头需保持一定距离以避免弛豫过程中试样与刮头之间的相互作用. 驰豫结束后，在微正则系综下进行刮擦过程的模拟. 在刮擦过程中，刮头在300 K的初始温度下以100 m/s的速度从初始位置沿着X轴负方向进行刮擦，刮擦深度设置为1.2 nm. 需要指出的是，已有分子动力学模拟工作将刮头的速度设置为100 m/s，并捕获了划痕过程的主要物理特征[21,23]. 模拟过程中时间步长设置为1 fs. CoCrFeMnNi高熵合金之间的相互作用采用考虑第二近邻的修正嵌入原子势来进行描述[14]，其基本表达式为

式中，E是系统的总能量，Fi是嵌入能函数，是第i个原子处的背景电子密度，Sij和φij(Rij)分别是原子i和j在距离Rij处的屏蔽函数和对势.

金刚石刮头与基底之间的相互作用采用Lennard-Jones (L-J)势描述，其基本表达式为

式中，ε为能量参数；σ为距离参数；r为两个原子之间的距离. 根据Rappe等[25]计算的通用力场参数和Lorentz-Berthelot 混合法则[26]，金刚石刮头与基底之间的相互作用参数列于表1中.

本文中采用开源代码LAMMPS[27]进行模拟计算，采用位错提取算法[28]分析CoCrFeMnNi高熵合金在刮擦过程中出现的位错和结构特征，使用OVITO软件[29]对模拟结果进行可视化分析.

Fig. 1 Schematic diagram for simulating the scratch behavior of single crystal CoCrFeMnNi high-entropy alloy图 1 模拟单晶CoCrFeMnNi高熵合金刮擦行为的MD模型示意图

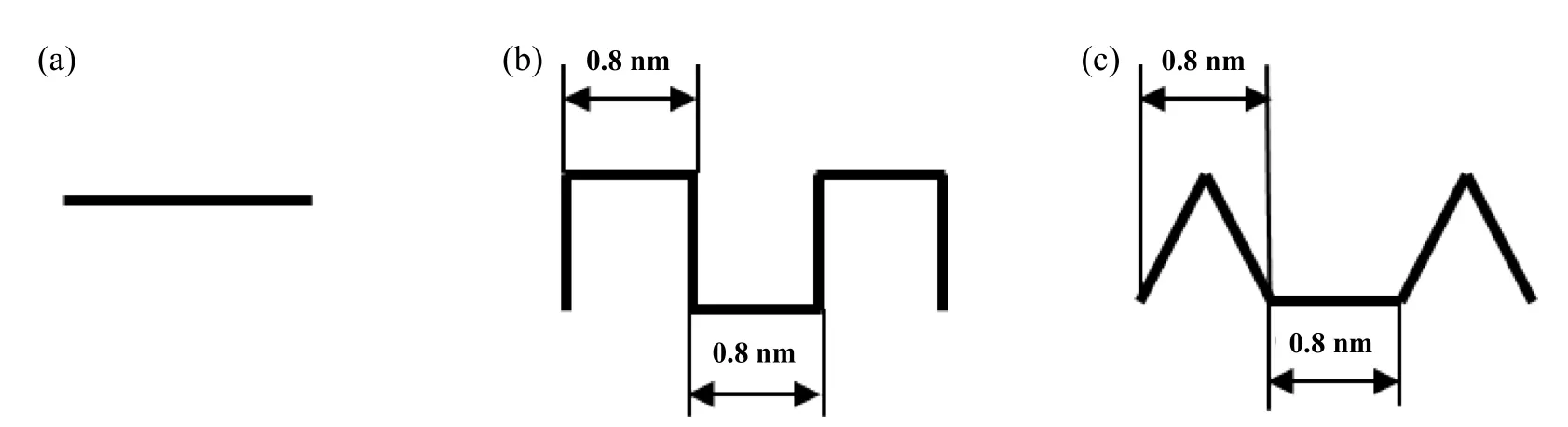
Fig. 2 The surface texture types of high entropy alloy: (a) planar,(b) rectangular and (c) triangular图 2 高熵合金表面形貌示意图：(a) 平面、(b) 矩形和(c) 三角形

2 结果与讨论

2.1 表面形貌对刮擦的影响

图3所示为不同表面形貌下，CoCrFeMnNi高熵合金刮擦过程中切向和法向刮擦力随刮擦时间的变化.由图3可知，随着刮头接近和切入基底，不同表面形貌试样的切向和法向刮擦力均从0开始不断增加. 随后刮擦力大致在一定范围内稳定波动. 取刮头完全刮入基底到刮擦结束时切向力和法向力的平均值作为平均切向力和平均法向力，平均切向力和法向力的比值作为平均刮擦摩擦系数. 图4所示为平面、矩形和三角形表面形貌试样的平均刮擦摩擦系数. 平面、矩形和三角形的平均刮擦摩擦系数分别为0.86、0.71和0.57. 这表明在1.2 nm的刮头半径中三角形形貌的减摩效果最明显，矩形形貌的减摩效果次之，光滑表面的摩擦阻力最大.

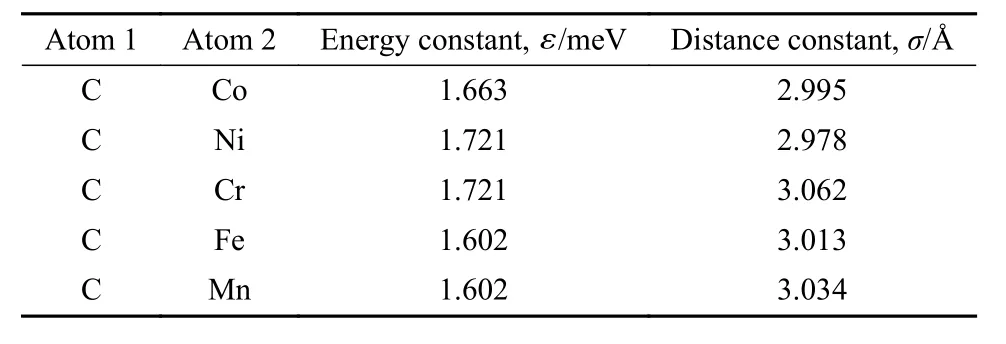
表 1 模拟中使用的 L-J势能参数Table 1 L-J potential energy parameters in MD simulations

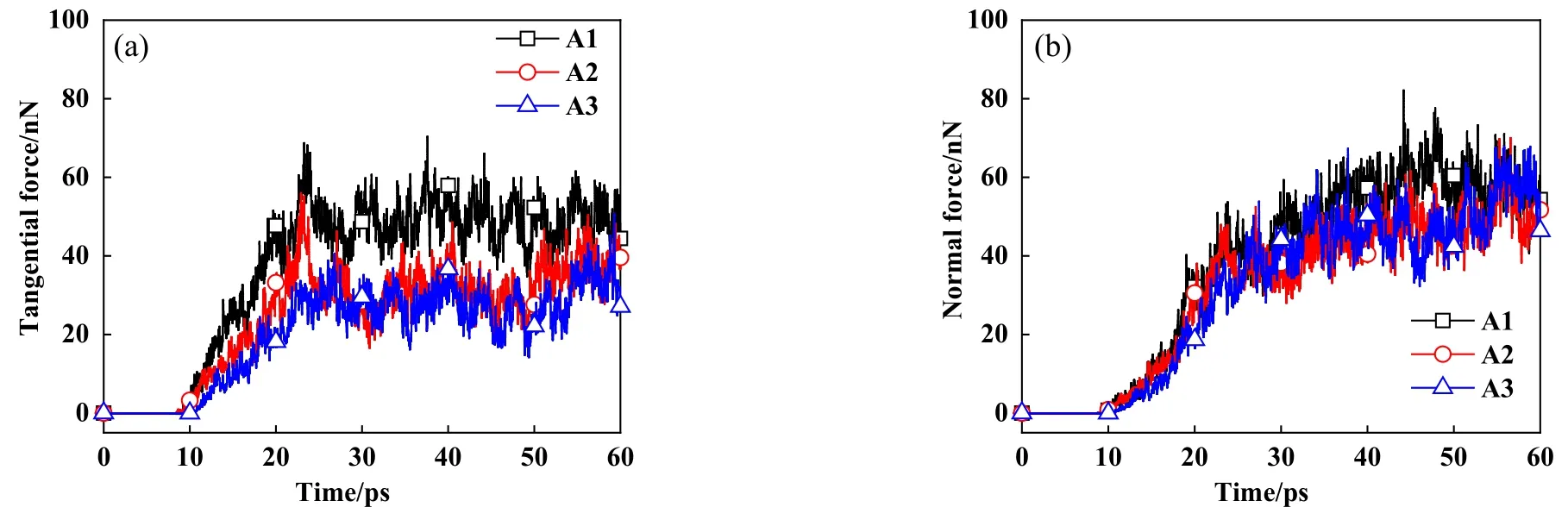
Fig. 3 (a) Tangential force-time curve and (b) normal force-time curve with different surface texture types图 3 不同形貌下试样(a) 切向刮擦力与时间的曲线和(b) 法向刮擦力与时间曲线

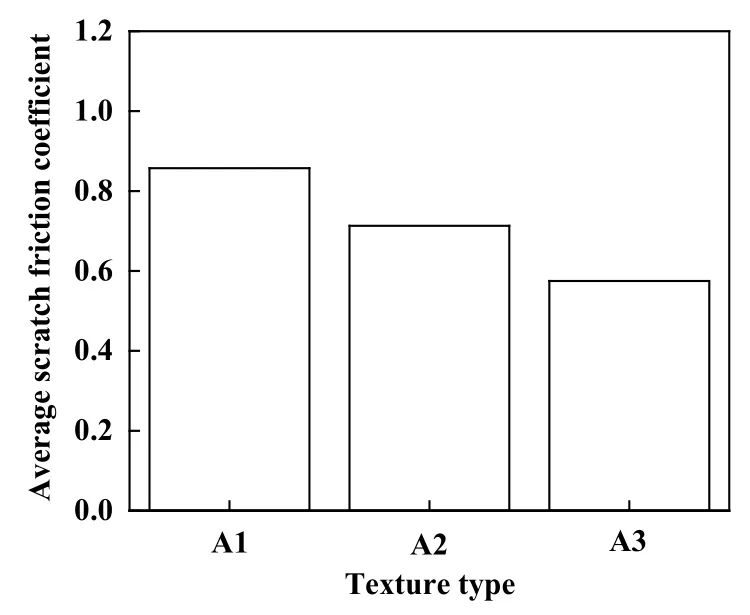
Fig. 4 Average scratch friction coefficient of planar,rectangular and triangular surface texture types图 4 平面、矩形和三角形表面形貌试样的平均刮擦摩擦系数

图5 所示为3种不同表面形貌的高熵合金在刮擦结束后的原子结构图. 如图5(a)所示，对于非平面形貌的试样，刮头后方的基底齿槽在刮擦变形后完全破坏，并且对应的基底齿槽的晶格呈现严重畸变. 对于平面形貌，刮头前方的表面向上凸起且不平整，对于矩形和三角形形貌，刮头前方的齿槽出现原子堆积.这表明刮擦变形后刮擦区域的基底以晶格畸变的方式被破坏并出现原子堆积.

如图5(b)所示，大量原子堆积在刮头前方，部分原子堆积在刮擦沟槽两侧，刮头前方原子堆积的高度大小依次为A1＞A2＞A3. 由此得知，刮头半径为1.2 nm时，刮擦载荷作用下CoCrFeMnNi高熵合金的晶体结构变形具有形貌依赖性，非平面类型的表面形貌有助于释放内应力，避免原子堆积.

图6所示为刮擦结束后不同形貌试样内部位错分布图，在刮擦过程中刮痕区域的位错以Shockley不全位错为主. 这表明CoCrFeMnNi高熵合金在刮擦过程中的主要塑性变形机理是Shockley不全位错的滑移变形. Qi等[22]也观察到CoCrFeMnNi高熵合金在单轴拉伸变形过程中的塑性变形以Shockley不全位错为主.图7所示为刮擦过程中不同形貌下试样的位错长度变化，由于能量最小化原理和弛豫过程中原子位置的调整，矩形类型的初始模拟晶胞会出现少量的位错. 当位错滑移到CoCrFeMnNi高熵合金表面时，表面会吸收位错，这使得位错线长度随着刮擦时间的增加而波动. 对比刮擦起始和终止时刻位错长度的变化，可以发现：A1类型的位错长度变化最大，其他2种形貌试样的位错长度变化率均小于A1.

Fig. 5 The atomic structure of different surface texture types after the scratch: (a1,a2) planar,(b1,b2) rectangular and (c1,c2)triangular (in a2,b2 and c2,the atoms were colored according to the height value)图 5 不同表面形貌下刮擦结束后的原子结构图：(a1,a2) 表面形貌为平面，(b1，b2) 表面形貌为矩形结构，(c1，c2) 表面形貌为三角形结构(在a2，b2和c2中，原子颜色根据高度值标记)

Fig. 6 Dislocation distribution in the simulation cells with different surface texture types after the scratch (the green lines were Shockley partial dislocation,the red lines were other dislocations)图 6 刮擦结束后不同形貌试样内部位错分布(绿色线条是Shockley不全位错，红色线条是其它位错)

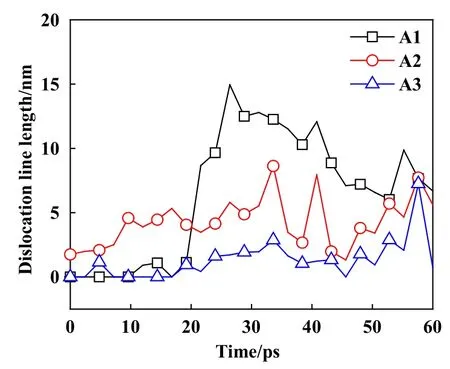
Fig. 7 Total length of dislocations in the simulation cells with different surface texture types during the scratch图 7 刮擦过程中不同形貌试样的位错总长度

当刮头进入基底并且划痕区域的外加载荷超过位错的形核应力时，位错从刮头周围的原子中形核生长并诱发刮擦区域的塑性变形，进而引起划痕区域原子的去除. 当划痕区域的塑性变形更加剧烈时，刮头前方会堆积更多的原子，从而增加划痕区域的摩擦系数[30-31]. 如图7所示，刮头完全进入基底后，也即大约22 ps以后，平面类型的位错总长度显著大于非平面类型的位错总长度. 这表明平面类型划痕区域的塑性变形比非平面类型划痕区域的塑性变形更加剧烈. 因此，平面和非平面类型划痕区域的摩擦系数与划痕区域的位错缺陷特征有关，位错诱发的塑性变形越剧烈，划痕区域的摩擦系数越大.

2.2 刮头半径对刮擦的影响

图8所示为不同刮头半径和不同表面形貌下材料的平均切向刮擦力、法向刮擦力和平均刮擦系数值.如图8(a)和(b)所示，平面、矩形和三角形表面形貌的平均切向力和平均法向力都随着刮头半径的增大而增大，这表明平均切向力和平均法向力具有刮头半径依赖性. 如图8(c)所示，对于不同的基底形貌，随着刮头半径的增加，平均刮擦系数均逐渐减小；在不同的刮头半径下，平面类型表面形貌的摩擦系数高于矩形和三角形类型表面形貌的摩擦系数；在刮头半径为1.2 nm时，矩形类型表面形貌的摩擦系数高于三角形类型表面形貌的摩擦系数，但是在刮头半径为0.6 和1.8 nm时，矩形和三角形类型表面形貌的摩擦系数不是单调变化. 非平面类型的表面形貌有助于释放内应力，避免原子堆积，另外，由于分子动力学模拟过程中热波动的影响，统计获得的切向和法向载荷会出现波动，这导致在刮头半径为0.6 和1.8 nm时，矩形和三角形类型表面形貌的摩擦系数出现波动.

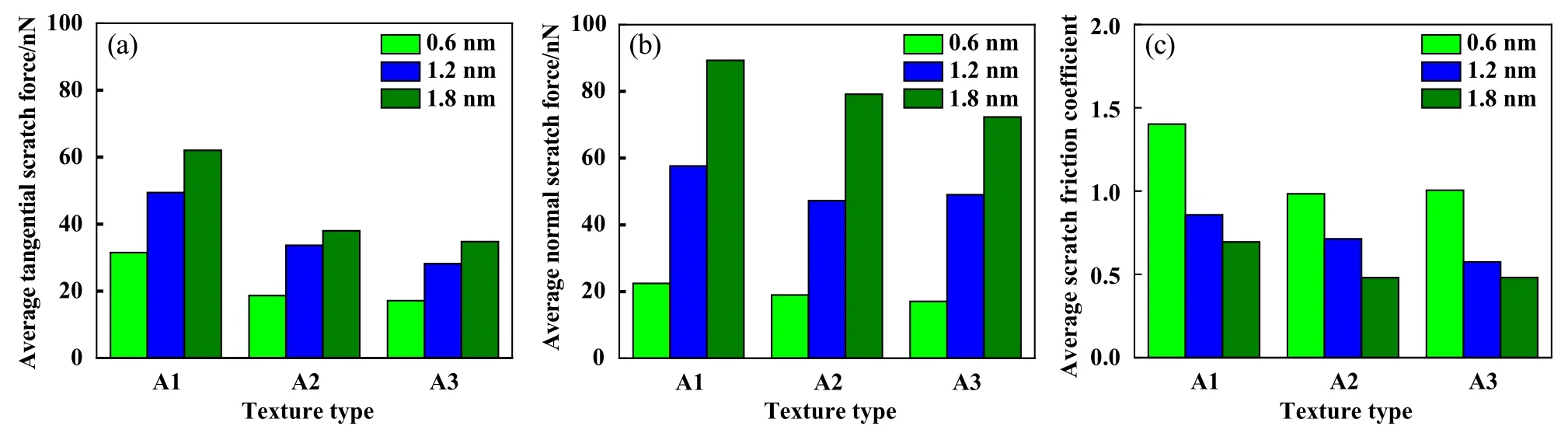
Fig. 8 (a) Average tangential scratch force,(b) average normal scratch force and (c) average scratch friction coefficient with different scratch tip radiuses and surface texture types图 8 不同刮头半径和不同表面形貌下材料的(a)平均切向刮擦力，(b)平均法向刮擦力和(c)平均刮擦摩擦系数

Fig. 9 The atomic structure of different scratch tip radiuses after the scratch: (a～c) 0.6 nm; (d～f) 1.2 nm; (g～i) 1.8 nm图 9 不同刮头半径下刮擦结束时刻的原子结构：(a～c) 0.6 nm；(d～f) 1.2 nm；(g～i) 1.8 nm

不同刮头半径下的刮擦结果更进一步表明，在CoCrFeMnNi高熵合金中，平面类型形貌的平均切向力和平均法向力显著高于非平面形貌的平均切向力和平均法向力；平面类型的形貌试样具有最大的摩擦系数；表面的非平面形貌有助于减小摩擦系数并具有明显的减摩作用，这与纳米尺度下不同形貌的单晶铜在高速刮擦过程中的研究结果是一致的[23].

图9所示为不同刮头半径下刮擦结束后的原子结构图. 刮头划过后，不同刮头半径和不同表面形貌的试样都发生了晶格变形和原子堆积. 随着刮头半径的增加，平面类型表面形貌的原子堆积高度明显大于矩形和三角形类型表面形貌的原子堆积高度. 在平面、矩形和三角形类型表面形貌照片中，刮头前方原子堆积高度均随着刮头半径的增大而增大.

图10所示为不同刮头半径下刮擦结束时刻单晶CoCrFeMnNi高熵合金中的位错分布. 随着刮头半径的增大，平面类型表面形貌中位错的长度和数量明显增加，但是三角形和矩形形貌中位错的长度和数量没有明显增加. 由于矩形和三角形类型表面形貌的刮擦区域并非连续，这使得矩形和三角形形貌中的位错更易于滑动到材料表面. 当位错滑移至材料表面时，表面会吸收位错，导致随着刮头半径的增加，矩形和三角形类型表面形貌刮擦区域的位错数量没有明显增加. 这表明刮擦过程中CoCrFeMnNi高熵合金表面的非连续形貌有助于位错的湮灭和降低刮擦区域的塑性变形. 这也进一步指出在1.2 nm的刮擦深度下，表面的非平面形貌通过位错湮灭的方式来减小摩擦系数，降低刮擦区域的塑性变形. 在图10中，不同刮头半径下刮擦结束时刻单晶CoCrFeMnNi高熵合金中的位错以Shockley不全位错为主，这表明CoCrFeMnNi高熵合金在刮擦过程中的主要塑性变形机理是Shockley不全位错的滑移变形.

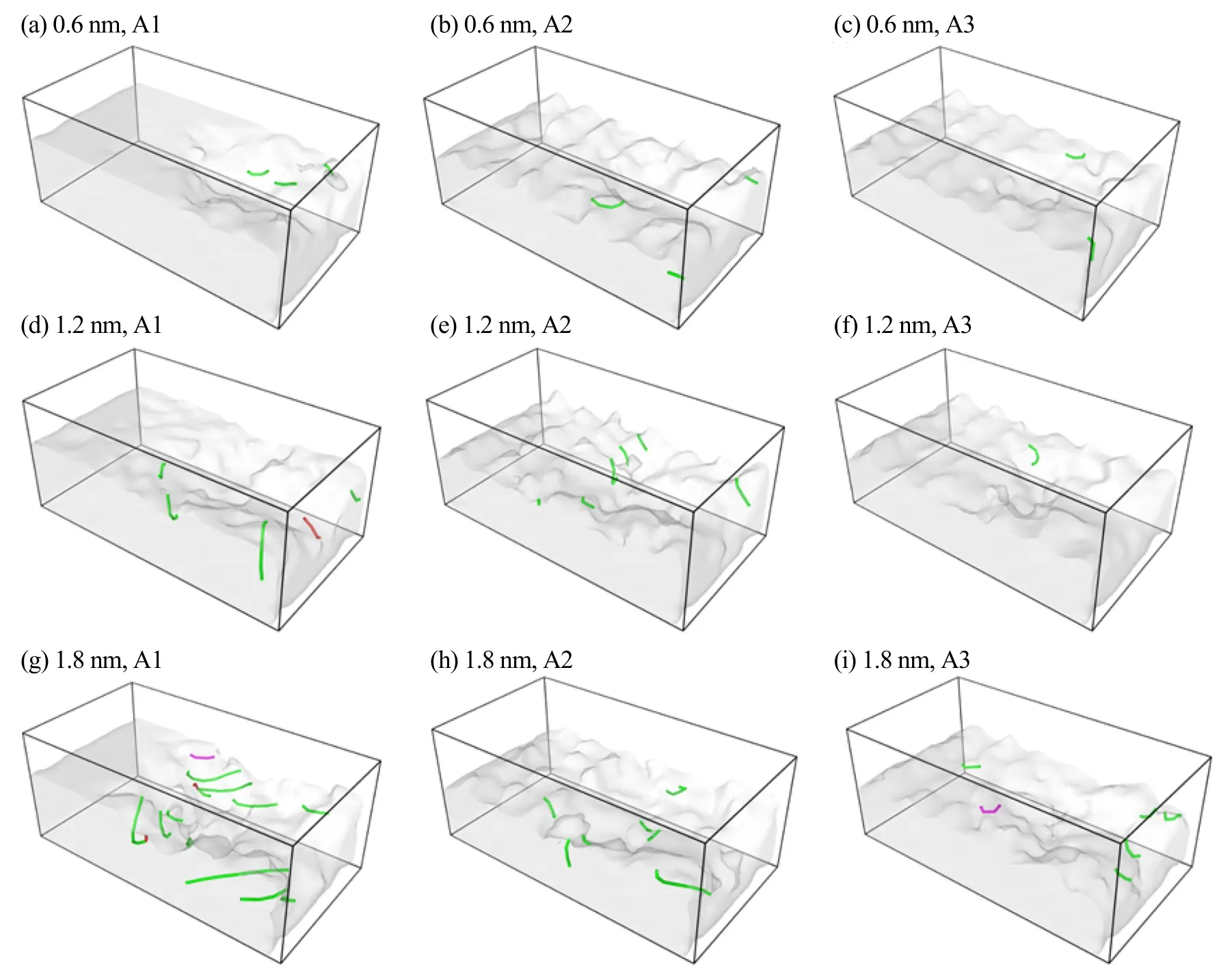
Fig. 10 Dislocation distribution in the single crystal CoCrFeMnNi high-entropy alloy with different scratch tip radiuses after the scratch: (a～c) 0.6 nm,(d～f) 1.2 nm and (g～i) 1.8 nm (the green lines are Shockley partial dislocation,the pink lines are Stair-rod partial dislocation,the red lines are other dislocations)图 10 不同刮头半径下刮擦结束时刻单晶CoCrFeMnNi高熵合金中的位错分布：(a～c) 刮头半径为0.6 nm；(d～f) 刮头半径为1.2 nm；(g～i) 刮头半径为1.8 nm (绿色线条是Shockley不全位错，粉色线条是Stair-rod不全位错，红色线条是其他位错)

2.3 MD模拟结果的验证

由于MD模拟中设定的加载率比现有的试验结果高多个数量级，现有研究主要定性地比较MD模拟与试验结果[32-35]. 通过与已有试验结果的定性比较，本文中详细讨论了MD模拟结果的合理性.

Nagarjuna等[20]开展了CoCrFeMnNi高熵合金的刮擦试验研究，指出CoCrFeMnNi高熵合金的摩擦系数随着刮头滑移时间的增加而趋于稳定. MD模拟也观察到CoCrFeMnNi高熵合金的切向载荷、法向载荷和刮擦系数随着刮擦时间的增加而趋于稳定. MD模拟获得的CoCrFeMnNi高熵合金的刮擦系数与时间的变化趋势与试验揭示的结果一致.

在室温下，Wu等[36]通过原位中子衍射试验说明了CoCrFeMnNi高熵合金在变形过程中形成许多不同取向的宏观滑移带. Yao等[37]利用金相显微镜进一步观察到室温下拉伸过程中CoCrFeMnNi高熵合金表面滑移线数量随着应变的增加而逐渐增加，并揭示了CoCrFeMnNi高熵合金的显微组织经历位错塞积、稠密位错墙形成和位错胞形成的演变过程. Laplanche等[38]、Otto等[39]和Smith等[40]的结果进一步表明位错滑移是CoCrFeMnNi高熵合金的主要塑性变形机理. Nagarjuna等[20]观察到CoCrFeMnNi高熵合金的刮擦区域存在位错滑移以及由剧烈塑性变形诱发的表面磨损. MD模拟结果表明当刮头进入基底时，位错在刮擦区域形核生长并诱发刮擦区域的塑性变形，进而引起划痕区域原子的去除. MD模拟获得的CoCrFeMnNi高熵合金的刮擦区域的塑性变形机理与试验的结论一致.

综上所述，通过比较本项工作获得的MD模拟结果与对应的宏微观试验结果，可以确定MD模拟是合理的，并进一步反映了CoCrFeMnNi高熵合金在原子尺度的刮擦行为及其变形机理.