一道创新性多选题的解法探究及高考溯源
2023-08-01王东海
王东海 王 晶
(1.安徽省合肥市肥东县城关中学 2.安徽财经大学会计学院)
2023年3月中学生标准学术能力测试数学第12题极具综合性和创新性,且其题干简洁,没有繁冗的文字,学生易想到使用数形结合法去处理.但此题融入了众多数学思想与方法的考查,对学生数学核心素养应用水平和关键能力有较高要求,因而正确求解并非易事.也正因如此,本题的得分率较低.同时,就笔者所进行的调查结果而言,本题的区分度好,不失为一道比较成功的多项选择题.
1 考题呈现
分析这道多选题考查了椭圆、点到直线距离等相关知识,检验了学生分析问题、解决问题的能力,除了运用常规的数形结合思想方法求解外,可以通过设而不求用根与系数的关系求解,也可以利用三角换元知识处理,还可以运用仿射变换巧妙破解.试题设计精巧、内涵丰富,是一道有探究价值的好题.
2 解法探究
视角1四个选项都可以看成P(x1,y1),Q(x2,y2)两点到同一条直线的距离之和的倍数的最值,而对于x1x2+9y1y2=-2,可使用常规的根与系数的关系去处理.
3 追本溯源
3.1 教材溯源
2023年中学生标准学术能力测试第12题是一道对思维能力有较高要求的好题,但它也不是无本之源,而是与教材有着紧密的联系,正是贯彻了高考命题源于教材、高于教材的理念.上述四种方法中方法4相对运算量较小,即利用仿射变换将椭圆变换成圆使求解更容易.事实上仿射变换实现椭圆和圆之间的转化现行教材早有渗透,它来源于人教A 版数学《选择性必修1》第108页例2:
如图1所示,在圆x2+y2=4 上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么? 为什么?
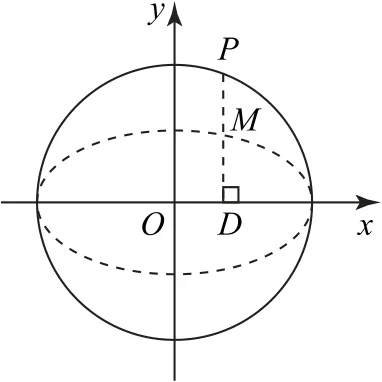
图1
之后教材还进一步给出一个思考:由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉伸”得到椭圆吗? 如何“拉伸”? 由此你能发现椭圆与圆之间的关系吗?
平时教学中只要将此例稍微引申一下即可理解仿射变换.另外,当问题转化为椭圆x2+9y2=1上的点到直线2x+3y-3=0和x-3y+5=0的距离的最值后,就成为教材中熟悉的题目,见人教A 版数学《选择性必修1》第116页习题13:
(1)它到直线l的距离最小? 最小距离是多少?
(2)它到直线l的距离最大? 最大距离是多少?
因此,笔者重视对课本例题与习题的挖掘,尤其是对教材中那些蕴含丰富的数学思想、开阔的思路的例题与习题的挖掘,针对这些好题,挖掘其中的数学背景,剖析背后的数学本质,感悟试题设计所蕴含的数学思想等,为高考打好基础.
3.2 高考溯源
4 一般性结论
5 结论应用
(完)
