多轴机电设备在线轨迹规划改进方法研究*

赵俊英，姚 彬，邵 欣，李云龙，韩金玉

（1.天津中德应用技术大学汽车与轨道交通学院，天津 300350；2.北京东方计量测试研究所，北京 100029；3.天津中德应用技术大学智能制造学院，天津 300350；4.天津中德应用技术大学基础实验实训中心，天津 300350）

0 引言

机器人等现代工业多轴机电设备中，运动控制一直是当前的研究热点［1-2］。轨迹跟踪精度和生产效率在高性能控制器［3］的设计研发中越来越受到重视。高进给速度能提高生产效率，但是可能会由于违反执行器的物理约束而导致控制器饱和以及跟踪性能下降等实际问题。因此，合理规划参考轨迹的进给速度对于提高生产效率并保证优良控制性能至关重要［4］。对此，Bobrowet 等利用序列二次规划技术求解了速度规划问题［5］。Renton 以及Stori利用数值搜索方法求解了时间最优轨迹规划问题，但计算效率较低［6-7］。Yuan 等提到的BFC 离线算法，不适用于需要实时在线轨迹规划的任务［8］。针对上述方法的局限性，Luet 等提出了一种双环在线轨迹优化算法，从实际结果来看，双环算法仅仅是接近最优的，因为当它在内环中积分时，参数加速度是不变的［9］。另外，在线轨迹规划的另一个框架采用了路径速度分解方案［10］和纵向时间标度［11］。基于此框架，Zanasi 等提出了一种实用的非线性在线轨迹规划器［12］。Bianco 等对文献［12］中的在线轨迹规划器进行了进一步扩展，利用有界估计器将转换后的参数速度和加速度输入到非线性滤波器，最后得到可行的参数轨迹［13-15］。此外，Bianco 在文献［15］中重点关注了在线轨迹规划的稳定性问题，引入了一种简单的阈值方法，当参数加速度下界的绝对值小于预设的阈值时，参数速度的上界设为零，实验结果表明该方法具有良好的性能。但当参数加速度上界小于其下界时必须辅以离线操作，削弱了在线轨迹规划的优势。

针对上述问题，本文提出了一种改进的在线轨迹规划方法来解决广义参数加速度约束的问题，消除了加速度参数上界和下界必须分别为正和负的限制，并从理论上给出了改进的在线规划算法的全局收敛性。为验证所提的方法，本文设计了椭圆轮廓跟踪仿真实验、复杂曲线轮廓激光雕刻实验，通过与已有方法对比验证了本文所提方法的改进效果。

1 问题描述

在轨迹速度分解中，轨迹通常以参数化形式表示如下［10］：

其中，qd为时变轨迹，P（s）为路径函数。

轨迹是时变的，因而可写成复合函数形式：

根据链式求导法则，轨迹的速度和加速度为：

2 改进的在线轨迹规划器

与文献［14］的框架类似，本文提出的在线轨迹规划器由边界估计器和改进的非线性变结构滤波器两部分组成。如图1 所示，在关节空间中分配的运动学约束将转换为参数空间中的参数速度和加速度的约束。将转化后的参数速度和加速度的界限和期望时变参数律反馈到非线性滤波器，在转化后的参数速度和加速度约束下，通过非线性滤波器在线规划期望时变参数轨迹。

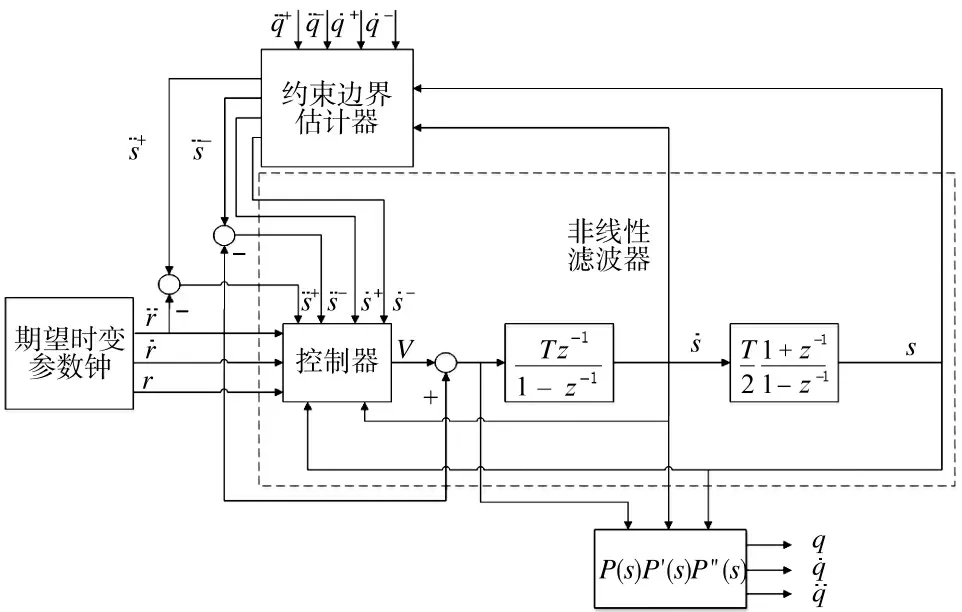
图1 在线轨迹规划框架Fig.1 Framework for online trajectory planning

2.1 边界估计方法

在关节上指定的速度约束可以用分量形式描述为：

式中，i 为关节编号，n 为最大关节数。关节的加速度约束可以描述为：

根据式（5），关节速度q˙i的约束条件可以很容易地映射为参数速度s 的一个上界，通过

可以得到参数速度的最终上界s˙+可以表示为

为避免规划的轨迹沿着路径产生反向运动，参数速度约束的下界s˙-设为零，即s˙-=0。

类似地，基于式（6）和式（4），可得参数加速度的上下界为

其中，

2.2 非线性滤波器的改进

在多轴系统轨迹规划中，参数加速度约束的上界和下界并不一定严格是正值和负值，针对该问题，本文提出了一种改进的非线性滤波器。对于一个期望时变参数函数r（t），以及由边界估计器提供的s˙+∊R+，s˙-=0，s¨+∊R+和s¨-∊R 等极限，所提出的非线性滤波器有望达到以下性能。

1）对于满足给定约束条件的可行参考轨迹r（t），即

期望达到的目标是滤波器的输出s（t）在最小的时间内达到跟踪性能s（t）=r（t），且无超调。

2）如果不满足式（13）中的约束条件，滤波器s（t）的输出应该以最佳的方式逼近参考轨迹r（t），即参数加速度s¨必须强制在一个执行周期内进入区间［］内，然后滤波器将在式（13）约束下保证其输出跟踪参考轨迹r（t）。

如图1 所示，以参数加速度作为控制输入，系统的动力学模型等效为两个积分器的串联。

引入si表示系统状态，且令si=［］T。则状态空间形式的系统动力学表示为［13］

其中，ui=，T 表示采样时间。

根据式（14）知，对于以下离散形式的参考输入

系统的误差动力学公式为

采用文献［14］中的变换来避免系统对采样时间T 的显式依赖

其中，

将式（17）代入式（16），则误差动力学重新表述为

其中，

由于矩阵W 的非奇异性，可以通过将状态z强制到原点来保证零跟踪误差，即yi=0。其次，设计一个非线性滤波器以保证zi的全局收敛性，该滤波器的第二状态变量和控制输入均受边界估计器的约束。

需要注意的是，文献［14］中的在线轨迹规划器只有在参数加速度的上下限分别为正和负的假设下有效，即>0 和<0。下面提出的非线性滤波器放宽了这一限制，并考虑了广义参数加速度约束∊R和∊R。为此，进行以下变换，得到参数速度和加速度的等价界：

其中，ε 是无穷小量且ε>0。

δ 的值由以下方程确定

参数γ，α，m 通过如下方法计算得到：

其中，式（30）表示参数的下限值。

非线性滤波器的最终控制输入为

上述控制器所采用的滑动面经过精心设计，公式如下：

3 在线临界曲线算法

4 实验验证

为验证所提算法的有效性，本文在双轴门架激光雕刻实验台上进行了椭圆轮廓跟踪仿真实验、复杂曲线轮廓激光雕刻实验，通过实验结果对所提出的在线轨迹规划器的优势进行分析。

如图2 所示，实验台主要由X 轴运动模组、Y轴运动模组、激光发生器、雕刻工作台、以及固定支架等组成。其中，X、Y 轴分别由一台伺服电机驱动，通过控制两电动机的运动，实现激光发生器在二维空间内的运动。在激光发生器运动的过程中，控制激光束的开关状态转换，即可在工件上雕刻出连续或间断的图案痕迹。

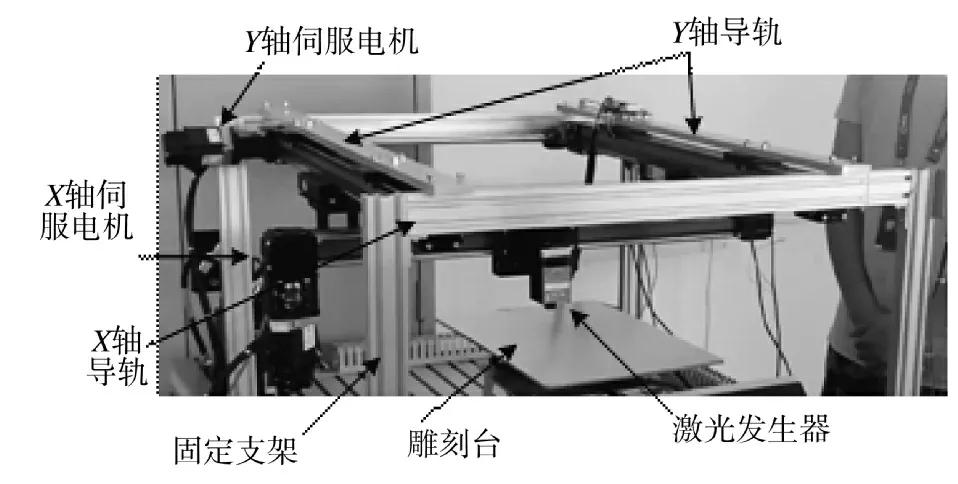
图2 实验平台Fig.2 The experiment platform

4.1 椭圆轮廓跟踪仿真实验设计

实验以椭圆轮廓作为跟踪目标，相对于圆形和方形等均匀曲线，椭圆的跟踪难度更大。本文所选的椭圆长半轴为0.1 m，短半轴为0.06 m，对应两个轴的位置、速度和加速度参考轨迹如图3 所示。由于轨迹为椭圆，且目标是在1.5 s 内沿椭圆轨迹运行一周，角速度固定，由此直接求导计算的两个轴的速度和加速度；实验中设置的速度和加速度约束条件为x 轴0.6 m/s 和6 m/s2，y 轴为0.4 m/s 和3 m/s2。

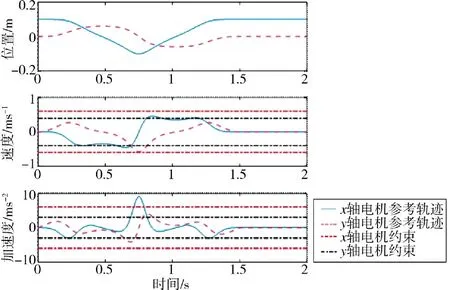
图3 椭圆轮廓参考轨迹Fig.3 Elliptic contour reference trajectory

从图3 可以看出，参考轨迹在速度、加速度上均有超出实际限制的情况，需要在线规划进行处理。此外，实验中采用自抗扰跟踪控制器对参考轨迹进行跟踪。同时，本文选择文献［14］中提出的轨迹规划器进行对比。

4.2 仿真实验轨迹规划结果分析

在椭圆轮廓跟踪仿真实验中，基于式（7）～式（10）和式（32），计算得到仿真曲线的轨迹规划结果，如图4 和图6 所示。通过比较本文方法和对比方法的轨迹规划结果，证明本文所提出的规划器能够解决广义参数加速度约束和两个潜在的稳定性问题。

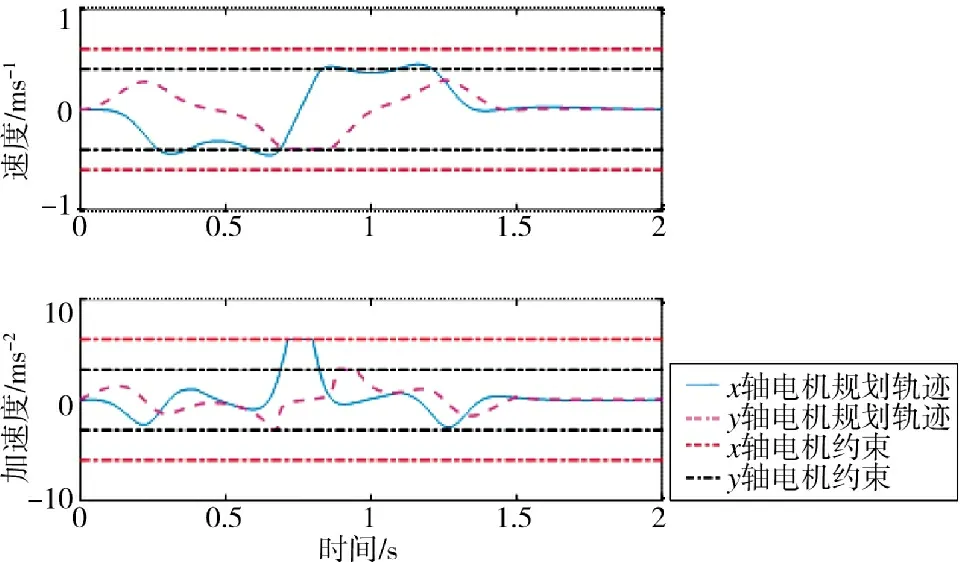
图4 本文方法的规划轨迹Fig.4 The planning trajectory obtained with the proposed method

规划器的采样周期设置为T=0.002 s，图4 和图5 都是matlab 仿真得到的曲线，分别为本文方法和对比方法的规划结果；如图5 所示，对比方法对应的轨迹规划结果仍然在个别情况下会超出对应的约束限制，仍然存在轨迹规划不理想的问题。从图5可以看出，对比方法的x 轴加速度规划值在0.72 s时超出给定上界，达到了7.43 m/s2，而且y 轴的加速度规划值同样在0.91 s 时达到了6.93 m/s2，两个轴的加速度规划值分别超过了设定加速度上限。

图5 对比方法的规划轨迹Fig.5 Planning trajectory obtained with the comparative method

相比之下，本文所提方法则可以很好地处理该问题，如图4 所示，本文方法轨迹规划结果都在电机约束范围内，规划结果符合物理约束，不会对电机执行规划的轨迹造成影响。通过对比，本文所提方法不会违反实验设置的约束条件。

4.3 仿真实验轨迹跟踪结果分析

利用本文方法进行了椭圆轮廓跟踪仿真实验，本文所用设备准确跟踪了经过在线规划的参考轨迹。为了更清晰地展示仿真结果，绘制了包含x、y 位置与时间进度的三维曲线，如图6 所示。与其对应的详细的速度、加速度规划曲线如图4 所示。

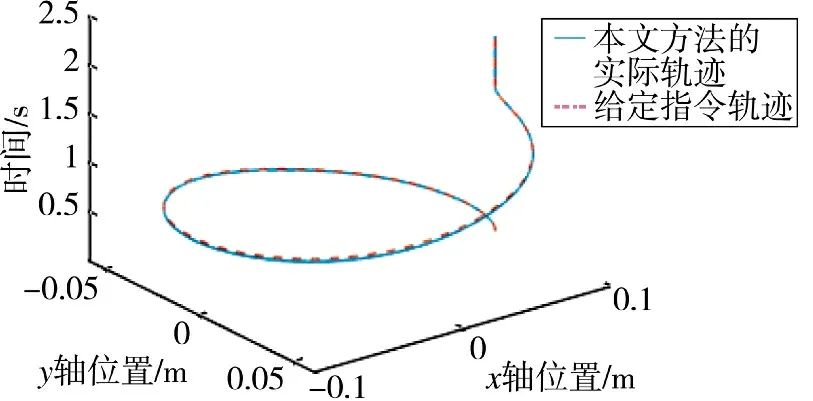
图6 轨迹跟踪实验Fig.6 Trajectory tracking experiment

图6 中的实线为实验曲线，分别是记录的x 轴和y 轴的位置，虚线是与仿真一致的曲线跟踪目标，即跟踪角速度固定的椭圆轨迹。采样和插补周期都是1 ms。为了便于观察，图6 将实验结果通过三维形式呈现，以清晰表达参考轨迹与本文规划轨迹之间的区别。图中坐标轴x 和坐标轴y 分别为x 轴和y 轴的位置，坐标轴z 则为时间。从图6 中可以看出，实际运行轨迹可以完成椭圆跟踪任务，实现对给定参考轨迹的跟踪，而且在t=0 的初始位置以及结束位置参考轨迹与实际轨迹重合。但是由于速度和加速度约束的限制，中间个别时间存在实际轨迹滞后于参考轨迹的现象，如图中红色虚线所示的玫红色虚线高于蓝色实线，这是由于参考轨迹的速度超出了电机轴实际可执行的速度或加速度。随着这段时间的结束，实验装置所输出的实际曲线将弥补这部分的滞后误差。

由图4 可见，本文方法可以很好地处理速度和加速度超出实际限制条件的情况。对应到图6 中，可以看到给定位置指令因速度和加速度超出实际限制而领先于实际输出值，但本文方法可以在后续计算中充分利用加速度和速度边界值实现规划误差的收敛，即实际输出跟踪上给定指令轨迹。综上，结合图4 与图5 所示规划结果对比，以及图6 所示轨迹跟踪实验曲线，可知本文方法可实现约束条件下对参考轨迹的最优跟踪。

4.4 激光雕刻应用实验

为了验证本文方法的实用性，应用本文设计的算法，以图7 所示图案为雕刻对象，在双轴门架激光雕刻实验台上进行了复杂曲线轮廓激光雕刻实验，其中，被雕刻木板的尺寸为200 mm*200 mm。

图7 激光雕刻图案Fig.7 Laser engraving pattern

观察图7 可知，待加工的图案不是简单的直线或圆弧等规则曲线，而是轮廓比较复杂的多次非线性曲线，激光头完全通过图案每一个点的难度很大。另外，由于激光雕刻工艺的特点，若轨迹规划不合理，很容易出现刻痕深浅不一、木板烧焦、精度差等雕刻质量低下的情况。综上，复杂轨迹激光雕刻对轨迹规划方法有较高的要求。

图8 所示为激光雕刻实验结果，由图可见，雕刻轨迹光滑、无突变；雕刻痕迹深浅均匀，木板上没有出现刻痕焦黑或烧焦的现象。进一步验证了本文轨迹规划方法的有效性及实际应用价值。

图8 激光雕刻实验结果Fig.8 The experiment result of the laser engraving

5 结论

本文提出了一种改进的在线轨迹规划方法，通过对在线轨迹规划器中非线性滤波器的改进解决了广义参数加速度约束问题。同时，本文算法取消了参数加速度的上界和下界必须分别为正和负的限制，在线算法的实现也解决了以往轨迹规划中可能存在的稳定性问题。椭圆轨迹规划和跟踪仿真实验验证了所提出的在线轨迹规划方法的正确性，证明了该算法在轮廓跟踪任务中取得了显著的性能改善；在试验台上进行的复杂曲线轮廓激光雕刻实验，进一步验证了本文轨迹规划方法的有效性及实际应用价值。