航母编队反无人机蜂群作战兵力部署模型及优化*

樊辉锦，巫银花，毕 月，刘家祺，苏泽亚

（1.海军指挥学院，南京 210018；2.解放军92635 部队，山东 青岛 266001；3.解放军92326 部队，广东 湛江 524001）

0 引言

随着自动控制、大数据和人工智能等技术的不断发展，无人机蜂群战术在实战中得到应用和发展［1］，以其高效费比、高自主性和低伤亡风险的特点成为新兴作战样式，给现代防空作战带来了新的挑战。同时，反无人机蜂群作战的研究还处于探索起步阶段，尤其对于航母编队这类高价值目标，反无人机蜂群作战能力建设需求日益迫切，如何调整现有兵力部署以应对无人机蜂群攻击成为研究重点。

目前，反无人机蜂群作战的相关研究主要集中在武器系统和作战能力评估方面［2-4］。焦士俊等利用模糊层次分析法对反无人机蜂群作战中雷达探测效能进行定量评估分析，并实例分析验证可行性［5］；姚立新等构建基于空间解析几何的防空火箭弹反无人机蜂群交会模型，提出利用激光引信提高反蜂群探测概率，并通过蒙特卡洛方法构建并分析反蜂群探测概率模型［6］；杨永亮等从弹炮结合反无人机蜂群角度出发，建立基于排队论的作战能力评估模型，并仿真分析其能力需求，主要从近程防御和火力拦截方面提出反无人机蜂群能力建设需求［7］；杨丽娜等从“任务- 能力”映射关系构建高能微波武器反无人机蜂群能力需求的解析模型，为装备发展需求论证提供支撑［8］；闫海港等明确了海上反无人机蜂群作战概念，分析蜂群作战优势及弱点，提出了海上防空体系反蜂群作战的多种方式［9］。总得来看，相关研究文献大多从武器系统或作战概念方面来进行反无人机蜂群作战分析，较少从海上编队体系作战角度来研究反无人机蜂群兵力部署问题。

本文以航母编队反无人机蜂群兵力部署为研究对象，重点分析编队内各兵力能力和装备有新兴反无人机蜂群武器作战平台部署位置和方位为变量的约束条件集，构建反无人机蜂群作战兵力部署解析规划模型，并采用智能优化算法寻优满足约束条件并使作战效能最大的解，为航母编队反无人机蜂群作战兵力部署提供参考。

1 航母编队反蜂群作战兵力部署模型

航母编队采用经典的远中近3 层防御体系，通过解析规则将反无人机蜂群作战任务转换为作战兵力部署需求，从而提出作战兵力部署要求，重点考虑对蜂群的打击和压制时外层电子战飞机和中层装备有反无蜂群武器防空警戒哨舰兵力部署情况。为便于理解，将文中涉及的物理量定义如表1。

1.1 反蜂群目标需求

以航母编队反无人机蜂群作战为背景，假设目标蜂群从编队防区外某方向以VUAVs速度向航母编队袭来，编队中层防区半径为RM，对无人机蜂群打击半径为RH，预警机有效预警半径为以航母为核心半径RAW的扇形区域，要求无人机蜂群被拦截和击落的概率为90%（或蜂群中90%以上的目标被拦截、控制或击落的概率），同时，航母编队反无人机蜂群作战打击半径RH尽可能大，有效作战扇面角ω尽可能大。根据作战需求提取目标约束要求为：

式中，P 为无人机蜂群被拦截和击落的概率，用来描述拦截效果。则P 可以表示为由兵力部署约束控制的函数，即

其中，RH为反蜂群打击半径，ω 为反蜂群打击半径扇面角，RAW为预警机有效预警半径。

1.2 航母编队反蜂群兵力部署约束

兵力部署约束主要描述防空体系中各兵力要素必须满足的条件，其中各要素之间存在相互关联和制约关系，其中，主要关系如图1 所示。O 为航母编队中心航空母舰位置，X 轴为蜂群距离航母的直线距离来袭方向。

1）反蜂群打击半径RH。装备有反无人机蜂群定向能武器的防空警戒哨舰部署在中层防御区，其前出距离RL，定向能武器作用距离RW，舰载电子飞机前出距离到中层防御区边界距离为RLA，舰载电子战飞机电磁压制半径为REA，RM为中层防御区半径，将中层防御区边界定义为防空哨舰最远打击距离，则有如下约束关系：

其中，RLA为舰载电子战飞机到中层防御区边界的距离，与预警机前出位置、探测范围及舰载机出动时间和效率以及无人机蜂群的速度相关，RM和REA为武器系统性能参数相对固定，RL中层防空哨舰前出距离主要影响反蜂群打击半径RH。综合式（2）、式（3），可将RH表示为由RL、Ra、α 约束的函数，记作f1：

2）反蜂群打击扇面角ω。本文固定中层防空哨舰数量为3 艘，3 艘防空哨舰的前出距离RLi，方位角为βi（i=1，2，3），部署在威胁轴附近的防空哨舰编为1 号舰，方位角为β1，另外两艘部署在威胁轴的两侧，它们的方位分别为β2和β3。防空哨舰在判明无人机蜂群来袭方向后，快速机动变化队形，改变前出距离和方位角，编队中间1 号防空哨舰机动至来袭方向，以应对蜂群袭击。部署方式如图2 所示，则其形成的反蜂群扇面角为ω：

图2 中层防空警戒哨舰阵位图Fig.2 Trench map of low-level air defense picket ships

同时，为使打击扇面全覆盖，且无人机蜂群能够进入防空哨舰攻击扇面内，需在发现蜂群后机动时满足以下要求：

综合式（5）、式（6），可将约束关系描述为：

3）预警机有效预警半径RAW。

预警机主要为舰载电子战飞机和防空警戒哨舰提供蜂群目标信息，预警机发现时间决定甲板待战电子战飞机与无人机蜂群相遇时间，影响实施电磁干扰压制时间，进而影响拦截效果。预警机在巡逻区巡逻时，巡逻阵位中心距航母的水平距离为其前出距离Ra，相对于威胁轴x→的方位角为α，预警机探测距离为Da，预警机有效预警距离为RAW，其解析关系如图3。

图3 预警机最远预警距离示意图Fig.3 Schematic diagram of the farthest early-warning distance of early warning aircraft

假设（x，0）为预警机捕捉到无人机蜂群时，根据图3，无人机蜂群的位置为：

同时，若要预警机能够成功在外层防御区探测到无人机蜂群，则要求，

设舰载电子战飞机出动时间固定，探测距离由武器装备性能决定，影响拦截效果主要空中待战预警机位置（Ra，α）决定，则根据式（8）、式（9），可将RAW表示为由预警机位置约束的函数，即：

4）反蜂群拦截效果分析建模

①在外层防御区，将无人机蜂群经过武器作用范围的时间作为衡量拦截效果的指标，假设蜂群以恒定速度VUAVs沿威胁轴x→方向向航母编队中心突防，蜂群不论是否被拦截均能飞行至内层防区，则无人机蜂群经过预警机探测范围的时间ty可表示为：

甲板待战舰载电子战飞机起飞后以VEA速度拦截无人机蜂群，与蜂群相遇后可一直对蜂群实施电磁干扰压制至中层防御区边界，将预警机探测到无人机蜂群的时刻设为T0，信息发回航母编队后舰载电子战飞机起飞准备时间为t01，电子战飞机起飞时刻为T1，经过t12时间的飞行后，在T2时刻可对无人机蜂群发起进攻，攻击时长为t23，无人机蜂群进入中层防御区时刻为T3。则无人机蜂群在外层防御区受舰载电子战飞机攻击时间为t23，则有：

则根据式（12）、式（13），电子战飞机攻击时长t23可以表示为由蜂群距航母的位置以及中层防御区边界约束的函数：

将拦截效果PEA近似为指数分布，p1为指数分布函数，可得到其拦截效果概率函数：

②在中层防御区，无人机蜂群受中层防空警戒哨舰反无人机蜂群武器攻击时间为：

其拦截效果PL近似为概率函数：

考虑到蜂群进入中层防区后不一定沿轴线突防，式中，加入反蜂群作战扇面角ω 以修正拦截效果。

故，反蜂群作战拦截效果P 为：

1.3 反蜂群兵力武器性能约束

根据现有和未来一段时间内定向能武器的发展水平，对电子战飞机电子干扰作战半径和扇面角约束如下：

REA电子战飞机压制半径，VEA电子战飞机速度。

1.4 兵力部署规划模型

根据上述对航母编队反蜂群作战过程中兵力部署需求和约束条件的定量分析，以及防空警戒哨舰阵位中心到航母航行方向的距离和方位角为主要变量，建立如下规划模型：

根据式（1）、式（4）、式（7）、式（10），有

战场环境的复杂多变，为使决策结果更加贴近实际、科学合理，在建立兵力部署数学规划模型的基础上，可将航母编队反蜂群作战兵力部署优化转换为约束条件集下的优化问题，借助简化粒子群智能优化算法，求取解空间中的最优满意解。

2 基于简化粒子群算法的兵力部署优化

根据反无人机蜂群兵力部署的解析规则可得满足要求的解空间，建立带约束的非线性规划最优解寻优模型，采用简化粒子群算法（simple particle swarm optimization，简称sPSO），构建适应度函数，实现对目标函数的寻优。相比于经典粒子群算法（PSO）和离散粒子群算法（DPSO），简化粒子群算法能够简化模型求解过程，缩短求解时间，加快收敛速度，在兵力部署这类需要及时调整作出指挥策略的过程中具有更好的适用性。

2.1 求解算法的选择

智能优化算法的研究中，较为成熟的有：遗传算法、蚁群算法、粒子群算法和鱼群算法，根据相关文献［10-11］对4 种算法的性能测试，可将4 种算法收敛速度和适应范围总结为下页表2。针对算法时效性较高的军事类问题，尤其是本文的兵力部署优化问题，为能在海战场对兵力兵器部署做成及时调整，故选用收敛速度最快的粒子群算法，求解连续函数求极值问题。同时，本文尝试利用收敛速度更快的简化粒子群法来求解上述模型问题。

表2 4 种智能算法特点和适用范围Table 2 Features and applicable scopes of four kinds of intelligence algorithms

2.2 简化粒子群算法

粒子群算法中的速度项Vid代表粒子移动的快慢，速度项并不能较好地使粒子寻找到最优解，反而在迭代次数不够多的情况下出现“发散”，减低收敛速度［12］。而简化粒子群算法不包含速度项，具有参数少、结构简单、计算便捷等优势，公式为：

定义变量Xi={RL1，RL2，RL3，β1，β2，β3，Ra，α} 为3艘中程防空警戒哨舰反蜂群作战时前出距离和方位以及预警机前出距离和方位角向量，ri为（0，1）的随机因子，ci为学习因子，pid为当前最优位置，pgd为全局最优位置。避免了人为确定速度项Vid范围来控制收敛速度和精度。

2.3 适应度函数及初始粒子群

将第1 节中规划问题的目标函数作为粒子群算法的适应度函数，研究3 艘防空警戒哨舰的最优部署位置，适应度函数为：

粒子群算法中初始粒子群的位置会影响算法的寻优效率，反蜂群兵力部署优化中防空警戒哨舰的距离方位初始粒子群，应考虑现有综合防空队形中警戒哨舰的位置来设置，以求在航渡过程向作战过程机动变化队形时，机动距离较短，且提高搜索效率。

式中，RLiF代表航渡过程中防空警戒哨舰的位置，βiF代表航渡过程中防空警戒哨舰的方位。

2.4 简化粒子群算法流程

简化粒子群算法去掉速度项后流程如下：

Step 1：对粒子群进行初始化，设定粒子个数等参数，并将1.2 中规划问题的等式约束和不等式约束转化为约束集。

Step 2：对简化粒子群中每个粒子的适应度值和适应度函数进行求解，初始化个体最优pbest和全局最优gbest。

Step 4：比较适应度值和个体最优pbest，并更新。

Step 5：比较适应度值和全局最优gbest，并更新。

Step 6：判断是否达到迭代次数，未达到则返回Step 2 构成循环迭代，否则输出最优结果。

简化粒子群算法流程如图4 所示。

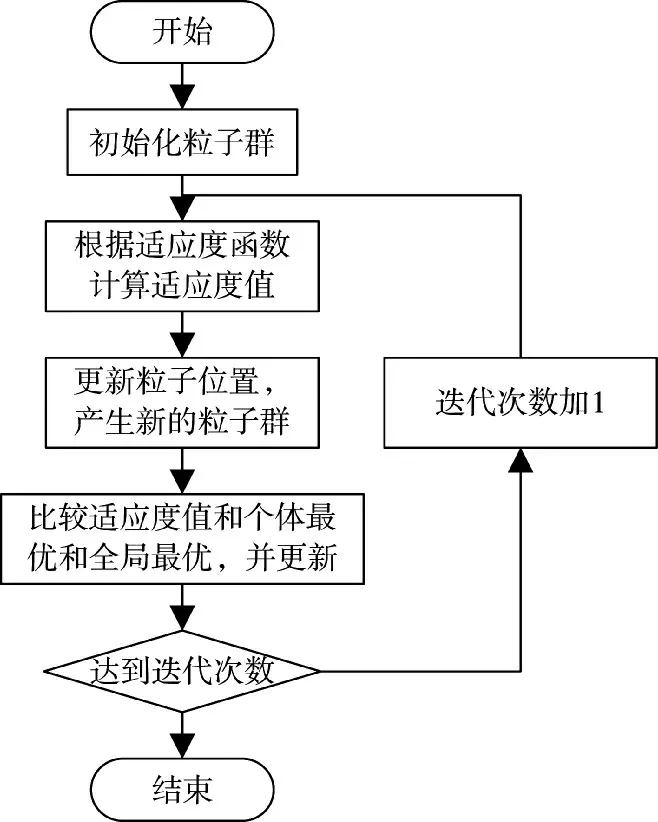
图4 简化粒子群算法流程Fig.4 Flow chart of simplified particle swarm algorithm

3 实例分析

本章根据上述模型和算法，构建航母编队反无人机蜂群作战想定，提出相关假设并设置参数进行实例仿真分析，将基于简化粒子群算法的求解方法与压缩粒子群算法、经典粒子群算法相比较求解过程和收敛速度，验证模型和算法的可行性和合理性。

3.1 作战想定

敌方无人机蜂群“蜂巢”（运载及回收无人机的平台，如飞机或水面舰艇）机动至我航母编队防区外100 km，投放出佯动诱骗群、电子干扰群和饱和攻击群等多组不同任务无人机蜂群，超低空自主飞行进入我编队外层防区，佯动诱骗群主动进入我雷达跟踪范围，分散其探测跟踪力量，诱使我编队启动舰载电子战飞机、防空导弹等高价值防御力量；电子干扰群携带电子干扰设备对我编队实施电磁压制，降低我编队的探测、识别、跟踪能力；饱和攻击群采取超低空机动突防，利用专用导弹、炸弹进行饱和式攻击或自杀式攻击，即使部分无人机被拦截依然可达到消耗我编队防空火力的目的，为后续进攻提供条件。过程中，主要考虑无人机饱和攻击蜂群，其主要目的为突破我航母编队3 层防空体系，主要目标为机动至核心航母所在内层防区并实施打击，摧毁高价值目标。

3.2 主要假设及参数设置

考虑到航母编队反蜂群作战的实际情况，将相关问题假设如下：

1）某无人机蜂群中无人机成圆形队形，以匀速直线运动接近航母编队，其速度为VUAVs，方位角θUAVs。

2）航母编队内中层防空警戒哨舰为同一类型，装备的定向能武器系统性能和杀伤范围相同。

3）定向武器对无人机蜂群杀伤程度与距离无关，只与无人机蜂群在杀伤范围内的时间有关，以蜂群圆心进入杀伤区时刻起算蜂群受攻击时间。

4）舰艇大小忽略不计，其阵位在图中用点表示，且当无人机蜂群经过定向能武器杀伤半径时，舰艇的移动不考虑。

综合考虑武器装备性能具体实例仿真参数数值或范围如表3，以下数据均为假设。

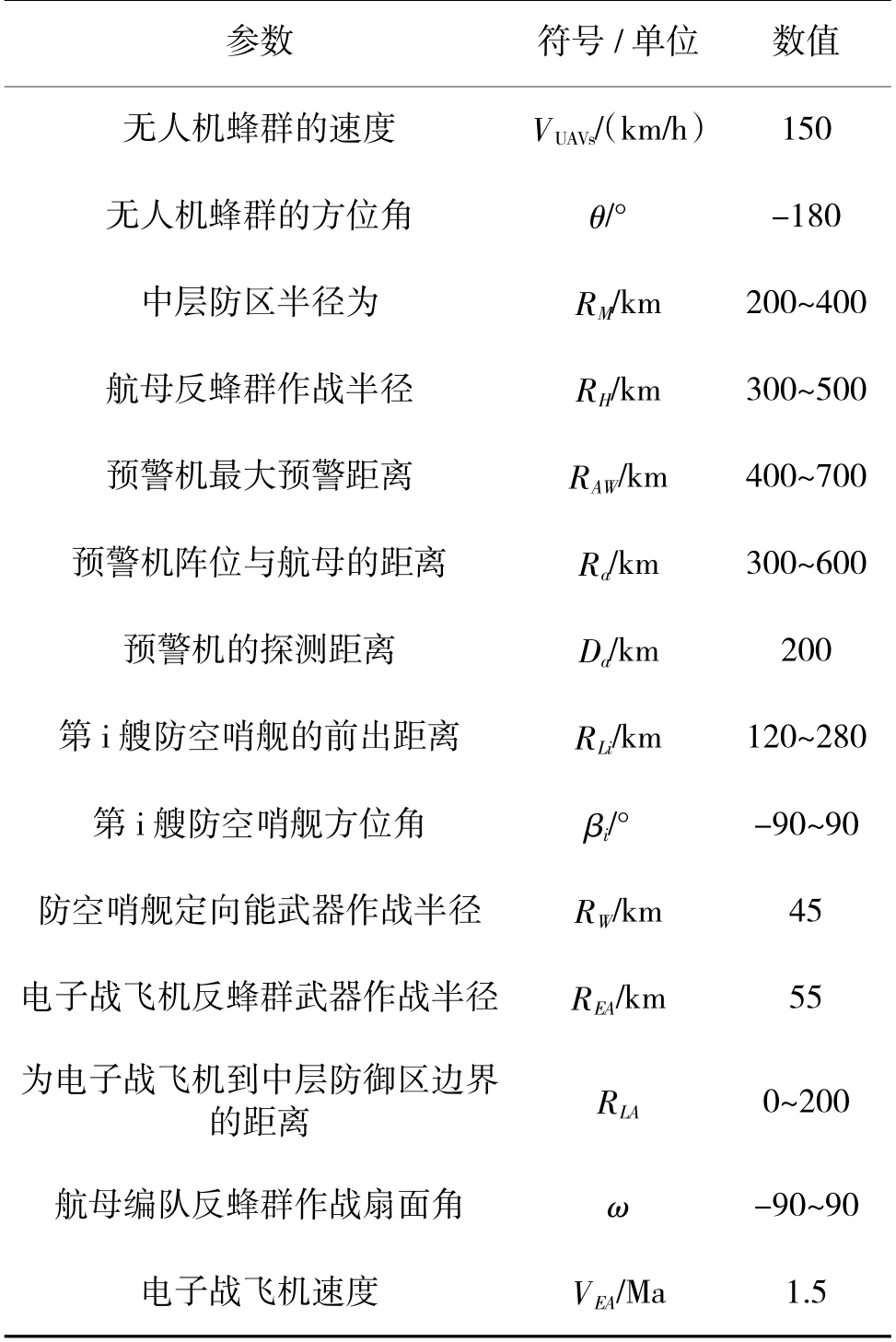
表3 实例仿真参数Table 3 The simulation parameters of the examples

无人机蜂群方位角设为-180°沿威胁轴方向向航母编队飞行，实例仿真用蒙特卡洛方法模拟蜂群来袭方位和速度，并进行简化粒子群算法寻优。将简化粒子群算法参数设置为：惯性因子ω=0.8，学习因子C1=C2=1，最大迭代次数为1 000。

3.3 仿真分析

本文仿真环境选用Intel Core i7-8565 3.2 Ghz四核处理器，内存为16 GB 的计算机来验证模型和求解算法，软件环境为Win7 操作系统，选用Matlab R2018a 进行仿真计算。实验过程利用表1 参数进行仿真实验，为降低偶然性，不同参数下每种算法均运行50 次记录最小、最大和平均值，3 种算法在不同参数下求解效率如表4 所示。

表4 sPSO 算法求解性能表Table 4 Solution performance table of sPSO algorithm

将不同粒子规模时不同算法的求解平均计算时间绘制成图5，可以看出，简化粒子群算法sPSO相比于其他算法在求解该模型时计算时间均较短，在计算性能上有一定的优势。

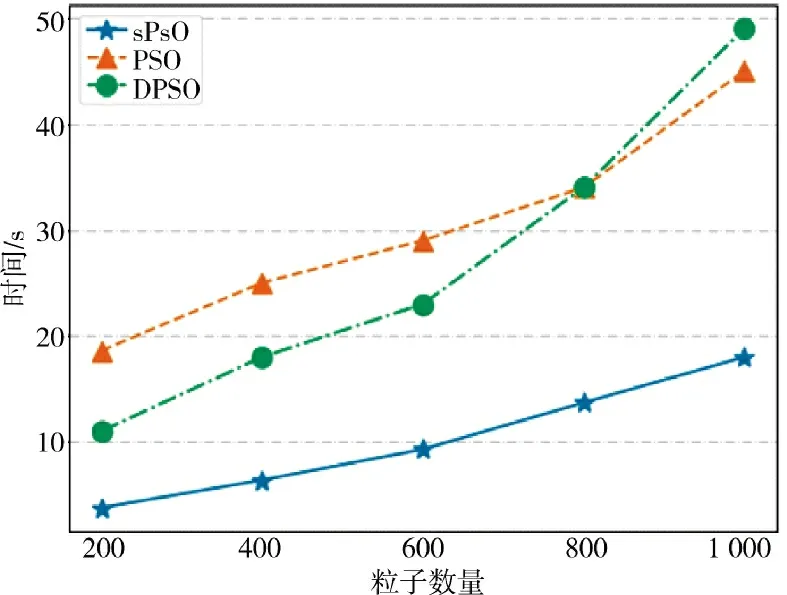
图5 算法运行时间对比Fig.5 Running time comparison of algorithms

对比粒子数量在600 时3 种算法的收敛速度，绘制图6～图8，可以看出，简化粒子群算法在迭代至400 次后趋于平稳时的迭代次数均小于经典粒子群算法和离散粒子群算法，说明简化例子群算法sPSO 在不同粒子群数量下，收敛速度均快于其余两种算法，求解精度满足要求，但小于其余两种算法，对于时效性要求更高的防空反蜂群作战而言在可接受范围内。

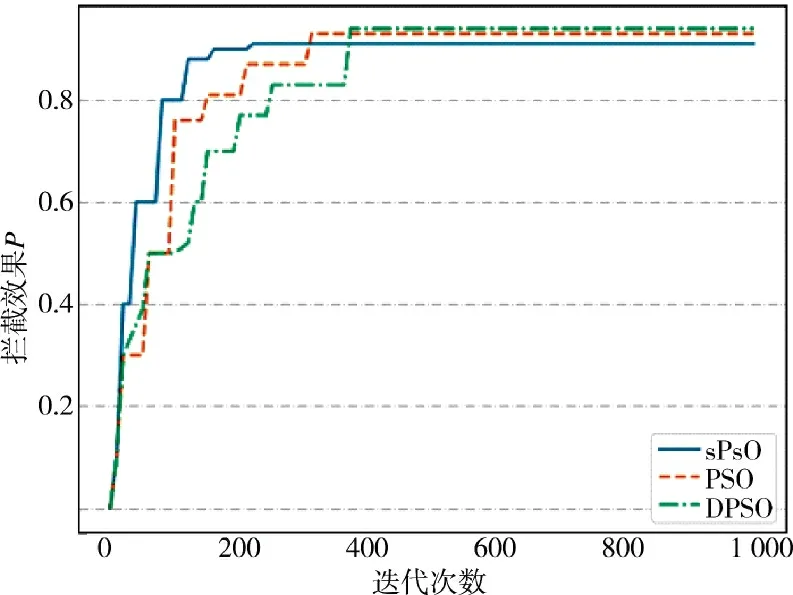
图6 拦截效果收敛图Fig.6 Convergence diagram of interception results

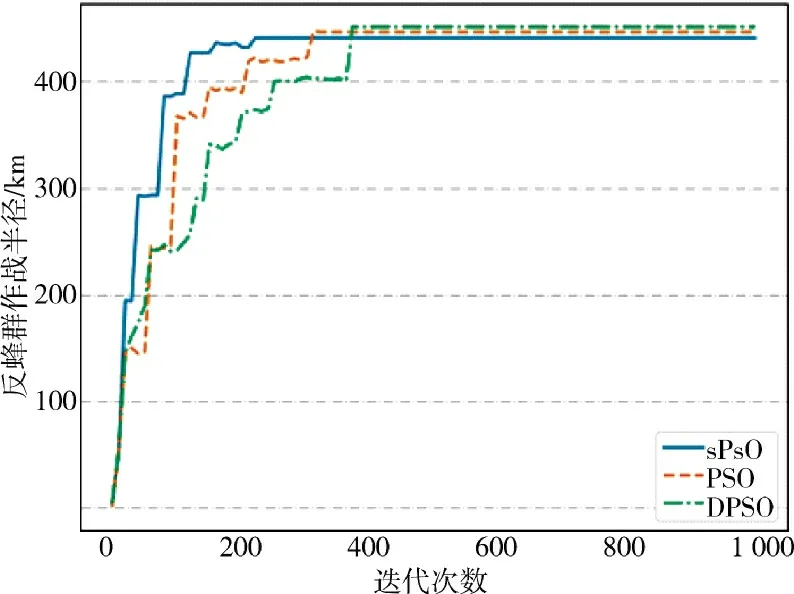
图7 反蜂群作战半径收敛图Fig.7 Combat radius convergence diagram of anti-swarm

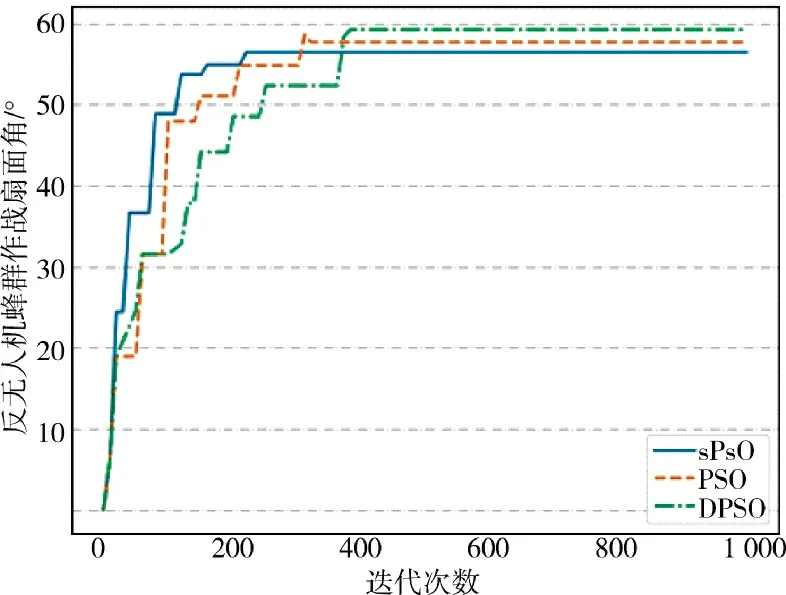
图8 反蜂群扇面角收敛图Fig.8 Sector angle convergence diagram of anti-swarm

综合比对收敛时间和收敛精度可以看出，简化粒子群算法在收敛时间上优势较大，收敛精度与其他两个算法接近，简化粒子群算法在求解兵力部署模型上具有一定优势，且结果得到了海军军事专家的认可，说明了模型和方法的可行性和合理性，具有一定的实用价值。

4 结论

本文从建立航母编队反蜂群作战兵力部署的解析规划模型入手，重点考虑中层防空警戒哨舰和舰载电子战飞机对蜂群的打击效果，并利用简化粒子群算法对解空间进行快速寻优，以便在战场环境中快速调整防空哨舰队形，抵御无人机蜂群来袭。同时，由于防空导弹反蜂群效费比较低，利用防空警戒哨舰定向能武器反蜂群效率更高，但需要防空哨舰作出较快的机动，且有一定的机动距离，对于慢速无人机蜂群适用。实例仿真结果表明该方法能较好地得到兵力部署方法，对实践有一定的指导意义和应用价值。不足之处，模型中假设较多，后续可根据需求进一步固化模型，研究不同无人机蜂群目标在不同速度、方向来袭时航母编队队形和机动方式，为航母编队反无人机蜂群作战提供支持。