有限温度下含三体相互作用的玻色-爱因斯坦凝聚体的集体激发特性
2023-07-28梁青青周小燕李好财
梁青青 周小燕 李好财


摘要:提出了一种描述有限温度下囚禁在谐振势肼中包含两体和三体相互作用的玻色-爱因斯坦凝聚体的自洽模型,利用该模型讨论了三体相互作用对凝聚体转变温度、凝聚体和非凝聚体密度分布和凝聚体集体激发频率的影响.利用求得的凝聚体基态波函数和集体激发的本征函数计算了集体激发模和准粒子的耦合矩阵元,得到了最低集体激发模的朗道阻尼,讨论了三体相互作用对最低激发模的朗道阻尼的影响.
关键词:三体相互作用;有限温度;集体激发;朗道阻尼
中图分类号:O 469 文献标志码:A 文章编号:1001-988Ⅹ(2023)04-0054-05
自观察到超冷玻色-爱因斯坦凝聚(Bose-Einstein condensate,BEC)的集體模以来,实验上对低能集体激发的测量[1]已发展到有限温度.在理论方面,描述凝聚体的格罗斯-皮塔耶夫斯基(Gross-Pitayefsky,G-P)方程已被推广到有限温度[2,3],并非常成功地解释了系统的热力学性质,如凝聚分数、内能、比热和临界温度[3,4].粒子间的相互作用会导致集体激发振幅的衰减(阻尼)和频率的改变(频移).在能级分离的系统中,集体激发的阻尼机制主要是朗道阻尼,文献[5-8]计算了BEC中低能模的朗道阻尼.然而,这些计算主要考虑两体相互作用[9-11];如果提高原子密度,三体相互作用将开始发挥重要作用[12-19].理论研究结果表明,即使较小强度的三体相互作用也会导致特殊的调制不稳定性[20],凝聚态的稳定区域和能谱也会有相当大的改变[21,22].文中将HFB-Popov近似推广到包含三体相互作用情形,研究了三体相互作用对凝聚体集体激发特性的影响.
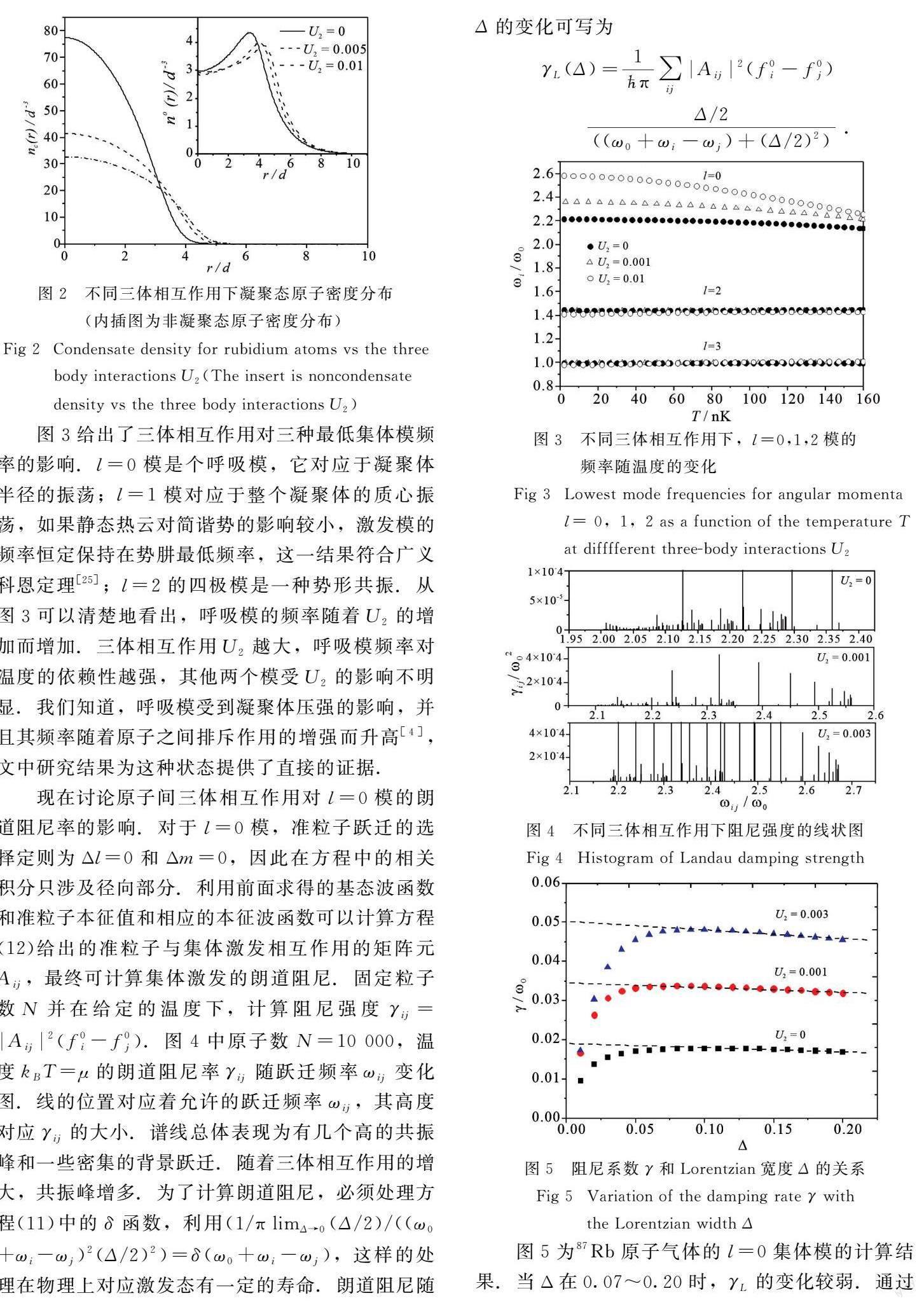
图5为87Rb原子气体的l=0集体模的计算结果.当Δ在0.07~0.20时,γL的变化较弱.通过将γ(Δ)的数据拟合为一条近似的直线,并将其外推到Δ=0,可以得到给定温度下集体激发模的朗道阻尼率.可以看到,阻尼率随着三体相互作用的增加而增加.
3 结论
文中将含时HFB-Popov近似推广到包含三体相互作用的情形,得到了一组耦合方程,通过数值求解这些方程研究了三体相互作用对凝聚体转变温度、凝聚体和非凝聚体原子分布、集体激发频率的影响.另外,利用所求得的基态波函数和集体激发的本征函数数值研究了三体相互作用对l=0集体模朗道阻尼的影响.计算结果显示三体相互作用会导致凝聚体转变温度减小,引起集体激发频率的移动,并能增强凝聚体最低激发模的朗道阻尼.
参考文献:
[1] JIN D S,MATTHEWS M R,ENSHER J R,et al.Temperature-dependent damping and frequency shifts in collective excitations of a dilute Bose-Einstein condensate[J].Phys Rev Lett,1997,78:764.
[2] GRIFFIN A.Conserving and gapless approximations for an inhomogeneous Bose gas at finite temperatures[J].Phys Rev B,1996,53:9341.
[3] GIORGINI S,PITAEVSKII L P,STRINGARI S.Scaling and thermodynamics of a trapped Bose-condensed gas[J].Phys Rev Lett,1997,78:3987.
[4] HUTCHINSON D A W,ZAREMBA E,GRIFFIN A.Finite temperature excitations of a trapped Bose gas[J].Phys Rev Lett,1997,78:1842.
[5] PITAEVSKII L P,STRINGARI S.Landau damping in dilute Bose gases[J].Phys Lett A,1997,235:398.
[6] GIORGINI S.Damping in dilute Bose gases:A mean-field approach[J].Phys Rev A,1998,57:2949.
[7] JACKSON B,ZAREMBA E.Landau damping in trapped Bose-condensed gases[J].New Journal of Physics,2003,5:388.
[8] GUILLEUNAS M,PITAEVSKII L P.Temperature-induced resonances and Landau damping of collective modes in Bose-Einstein condensed gases in spherical traps[J].Phy Rev A,2000,61:013602.
[9] MA Xiao-dong,MA Yong-li,HUANG Guo-xiang.Landau damping of collective modes in a disc-shaped Bose-Einstein condensate[J].Chin Phys Lett,2007,24:616.
[10] RAHMU T,ARZIGU L,PENG Sheng-qiang,et al.Landau damping and frequency-shift of a quadrupole mode in a disc-shaped rubidium Bose-Einstein condensate[J].Chin Phys B,2014,23:090311.
[11] MA Xiao-dong,YANG Zhan-jin,LU Jun-zhe,et al.Landau damping of collective mode in a quasi-two-dimensional repulsive Bose-Einstein condensate[J].Chin Phys B,2011,20:070307.
[12] GAMMAL A,FREDERICO T,TOMIO L,et al.Stability analysis of the D-dimensional nonlinear Schrdinger equation with trap and two- and three-body interactions[J].Phy Lett A,2000,267:305.
[13] ABDULLAEV F K,GAMMAL A,TOMIO L,et al.Stability of trapped Bose-Einstein condensates[J].Phy Rev A,2001,63:043604.
[14] AURE L,BULGA C.Dilute quantum droplets[J].Phys Rev Lett,2002,89:050402.
[15] THORST E N,KOHL E R.Three-body problem in a dilute Bose-Einstein condensate[J].Phys Rev Lett,2002,89:210404.
[16] LEANHARDT A E,CHIKKATUR A P,KIELPINSKI D,et al.Propagation of Bose-Einstein condensates in a magnetic waveguide[J].Phys Rev Lett,2002,89:040401.
[17] PIERI P,STRINATI G C.Derivation of the Gross-Pitaevskii equation for condensed Bosons from the Bogoliubov-deGennes equations for superfluid Fermions[J].Phys Rev Lett,2003,91:030401.
[18] ZHANG Xin,YU Zi-fa,XUE Ju-kui.Coherence of disordered Bosonic gas with two- and three-body interactions[J].Chin Phys Lett,2016,33:40302.
[19] CHANG Na-na,YU Zi-fa,ZHANG Ai-xia,et al.Tunneling dynamics of a few Bosons with both two-and three-body interactions in a double-well potential[J].Chin Phys B,2017,26:115202.
[20] ZHANG Wei-ping,WRIGHT E M,PU Han,et al.Fundamental limit for integrated atom optics with Bose-Einstein condensates[J].Phys Rev A,2003,68:023605.
[21] AKHMEDIEV N,DAS M P,VAGOV A V.Bose-Einstein condensation of atoms with attractive interaction[J].J Mod Phys B,1999,13:625.
[22] ZHANG A X,XUE J K.Band structure and stability of Bose-Einstein condensates in optical lattices with two- and three-atom interactions[J].Phys Rev A,2007,75:013624.
[23] DE GROOT S R,HOOYMAN G J,TEN SELDAM C A.Thermodynamics of diffusion in multicomponent systems[J].Proc R Soc London A,1950,203:266.
[24] BAGNATO V,PRITCHARD D E,KLEPPNER D.Bose-Einstein condensation in an external potential[J].Phys Rev A,1987,35:4354.
[25] DOBSON J F,HARMONI C.Potential theorem:implications for approximate many-body theories[J].Phys Rev Lett,1994,73:2244.
(責任编辑 孙对兄)
