离心压缩机磁流体密封设计及优化分析*

朱维兵 吴朝军 颜招强 王和顺

(1.西华大学机械工程学院 四川成都 610039；2.自贡兆强密封制品实业有限公司 四川自贡 643000)

随着石油、化工、煤化工等领域单套装置的处理规模越来越大，相应的离心压缩机大型化成为必然趋势，而其密封问题也成为一大难点。现有的迷宫密封、浮动环密封、机械密封及干气密封均有用于离心压缩机旋转主轴密封[1]，但都存在一定的缺陷：迷宫密封虽结构简单、辅助设备少、寿命长，但泄漏量大；浮动环密封可靠性高、对中性能好，但存在严重内泄漏，增加了设备复杂性；机械密封和干气密封类似，泄漏量低、运行稳定性高，但用于离心压缩机密封时，其动静环尺寸过大导致加工困难，同时干气密封还需复杂的辅助系统，且价格昂贵。而磁流体密封作为一种新型的密封方式，自问世以来，凭借其零泄漏、寿命长、可靠性高、无污染、承受高转速及黏性摩擦低等特点，被广泛应用于各领域[2-5]，也为离心压缩机密封困难的问题提供了解决思路。

目前，磁流体密封已是国内外密封领域研究的热点。LIU等[6]设计了一种带有保护层的磁流体密封装置，显著改善了密封液体介质的密封性能。李德才和杨文明[7]设计并搭建了大间隙磁流体静密封试验台，证实了其具有一定的实用价值。MIZUTANI等[8]为直线运动高精密仪器设计了一种磁流体密封装置，通过实验证明其具有良好的密封性能。TOMIOKA和MIYANAGA[9]设计了用于血浆泵的磁流体密封装置，并分别以气体、血浆、水为密封介质进行耐压测试，发现密封水时效果最差。张惠涛和李德才[10]设计了一种分瓣式磁流体密封装置，证明该结构具有良好的密封性能。邢斐斐等[11-12]设计了适用于大型船舶的一种五级九齿大间隙磁流体与磁性润滑脂组合的密封装置和高速离心泵用五极六靴二十四齿的磁流体密封装置，通过数值计算和实验手段，验证了设计的合理性。赵少迪等[13]利用磁流体对矿用带式输送机承载托辊实现了密封与润滑，为井下带式输送机密封技术的发展提供技术支持。袁芳等人[14]为大摆动幅度的旋转轴设计了一种径向轴向串联的磁流体密封装置，可有效提升其耐压稳定性。LI等[15]对大间隙磁流体密封液体装置进行优化设计，相比传统磁流体密封装置显著提高了其耐压性能和耐久性能。ZHANG等[16]研究了永磁体材料性能对磁流体密封失效压力的影响，发现磁流体密封的失效压力随着永磁体最大磁能积的增加先增加后减小。

综上，学者已将磁流体密封成功应用于不同领域，但将磁流体密封应用于离心压缩机并考虑离心力对密封性能影响的研究尚不多见。因此本文作者根据离心压缩机自身结构特点及工况要求，设计一种带降温和降压功能的新型磁流体密封装置；建立考虑离心力影响的磁流体密封耐压计算公式，利用有限元数值分析方法研究密封间隙内磁感应强度分布规律，探讨各结构参数对密封性能的影响，并通过响应曲面方法对各参数进行优选。

1 磁流体密封原理及理论

1.1 磁流体密封原理

磁流体密封原理如图1所示，其主要由永磁铁、极靴、磁流体、非导磁外壳、导磁旋转轴(轴套)组成[17]。通过利用磁流体对磁场具有响应特性，在高性能永磁铁、导磁极靴与转轴(轴套)之间形成的磁回路作用下，将注入转轴(轴套)与极靴间隙之间的磁流体牢牢吸附在极齿下方，形成多个“液态O形密封圈”，将间隙完全堵住，达到密封目的[18]。

图1 磁流体密封原理

磁流体密封圈工作时形状和位置随介质侧压力变化而变化，当液态密封圈左右两侧不存压差时，即p1=p2，磁流体密封圈液膜边界与磁感应强度等值线重合，对称分布，如图2(a)所示；当左侧压力高于右侧压力时，即p1>p2，磁流体密封圈在非均匀磁场中向右侧移动，导致左右两侧磁感应强度差值增大，磁流体所受磁场力增大，并由低压侧指向高压侧与压差平衡，如图2(b)所示。

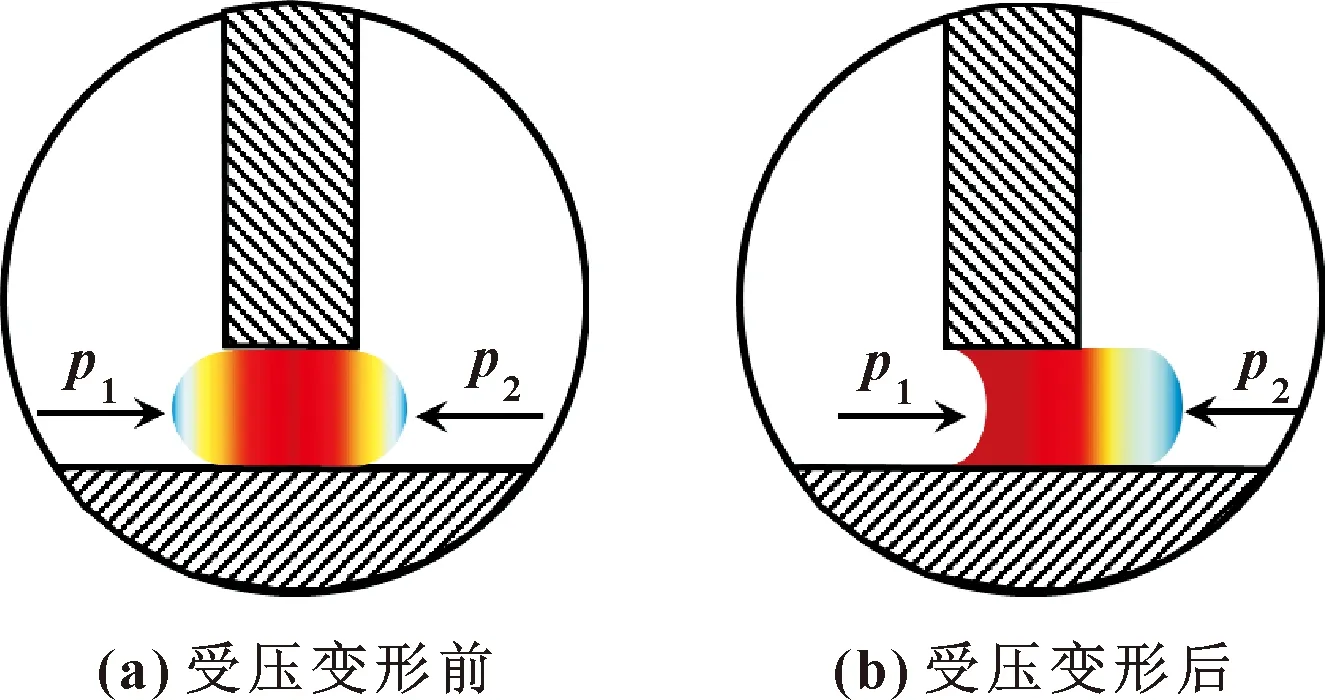
图2 磁流体密封圈工作变形

1.2 离心压缩机磁流体密封耐压理论

离心压缩机工作时由于其转轴转速高，导致磁流体密封圈受离心力作用明显。在离心力作用下转轴表面磁流体密封圈接触边界距离减小，分界面磁感应强度下降，密封性能降低[19]。所以高速旋转主轴磁流体密封耐压公式中需考虑离心力的影响。

当磁流体用于旋转密封时，密封间隙较小，通常假设磁流体为定黏度、不可压缩流体，磁化强度正比于密度，并忽略重力的影响，则磁流体的运动方程[20]为

(1)

式中：ρm为磁流体密度；v为磁流体速度；μ0为真空磁导率；M为磁流体磁化强度；H为磁场强度；∇p为磁流体所受压力梯度；ηH为动力黏性系数。

磁流体在密封间隙中做圆周运动，通常在柱坐标系(r，θ，z)下表达运动方程，又因磁流体密封圈轴向尺寸和径向尺寸相比于轴径小很多，所以其径向和轴向的速度为0，磁流体仅做切向运动，速度为半径的函数，与角度和轴向位置无关。且磁流体密封结构具有轴对称特性，所以柱坐标系下的磁流体运动方程为

式中：vθ代表磁流体速度的径向分量。

忽略磁流体两轴向端面的影响，认为磁流体在一个无限长的同心圆筒间隙中运动，所以磁流体运动速度与轴向位置无关，则得到：

若转轴半径为R1，极齿内径为R2，转轴角速度为ω0，如图3所示，则磁流体运动边界条件为vθ(R1)=R1ω0、vθ(R2)=0，代入上式求解得到：

图3 磁流体密封耐压分析模型

其中

将以上方程联合求解，得到：

(6)

式中：C为积分常数且

由图3可知线段14和线段23分别为高压侧和低压侧的等压线，所以得到：

将上式相减得到动密封耐压计算式：

(11)

在旋转轴静止时，最大密封值为2、4两点的磁流体膜耐压差值：

(12)

将式(11)与式(12)相减，并结合式(10)简化得到单极磁流体动密封压力计算表达式为

Δp=Δpmax+ρm(R1ω0)2Gc(Rs)

(13)

通常单级磁流体密封的密封压力偏低，所以实际应用中大多采用多级磁流体密封结构，且考虑到极齿下方磁场强度较大，认为磁流体处于饱和状态，所以多级磁流体旋转动密封压力计算表达式为

Δp=NΔpmax+Nρm(R1ω0)2Gc(Rs)=NMs(Bmax-Bmin)+Nρm(R1ω0)2Gc(Rs)

(14)

式中：N为密封级数；Bmax和Bmin分别代表极齿下方最大磁感应强度和最小磁感应强度；Ms表示磁流体饱和磁化强度。

2 磁流体密封装置结构设计

2.1 结构设计

根据企业提供的离心压缩机相关参数，进行磁流体密封装置结构设计，其中轴径为200 mm，转速为1 980 r/min，入口压力为0.127 MPa，温度为37 ℃，出口压力为0.26 MPa，温度为85 ℃，密封介质为一氧化氮(NO)。通过以上参数可知，轴径尺寸大、表面线速度高、密封压差大、工作温度范围宽，同时厂家要求“零泄漏”、高稳定性及长寿命。综上分析设计了一套带有降温和减压措施的磁流体密封装置，如图4所示。

图4 磁流体密封装置

该密封结构设有3个永磁铁、4个极靴、30个矩形极齿，相关结构参数根据文献[2]及密封装置安装尺寸进行初设，其中齿宽Lt=0.3 mm，齿高Lh=1.5 mm，密封间隙Lg=0.3 mm，槽宽Ls=2 mm，永磁铁轴向厚度Yh=3 mm，永磁铁径向宽度Yk=13 mm，轴套厚度Zh=14 mm。为防止离心压缩机启动时进口压力陡增冲破磁流体密封圈，在高压侧设有迷宫减压密封环；并考虑到转轴线速度较高，磁流体摩擦生热问题严重，如果单纯靠装置自身的热传导及自然对流很难将热量散发出去，导致密封装置温度升高，磁流体饱和磁化强度降低，永磁铁磁性降低，最终降低密封压力值，所以在密封外壳内设有冷却流道，工作过程中对密封装置进行降温，减小温度对密封性能的影响，保证磁流体密封装置的稳定性。

2.2 材料选择

由于磁流体密封装置中不同零件作用不同，所以选材也有所区别，轴套及极靴需要具有较强的导磁性能，因此选用10钢，其余非导磁金属材料选用304不锈钢。因文中设置的工况最高温度为85 ℃，所以根据GB/T 13560—2017选用NbFeB-N48H永磁铁，其磁剩Br=1.37 T，禀矫顽力Hcj=1 274 kA/m，磁通密度矫顽力Hcb=1 000 kA/m，最大磁积能(BH)max=390 kA/m，工作温度范围为20～100 ℃。磁流体选用自贡兆强密封制品实业有限公司生产的全氟聚醚油基磁流体，其饱和磁化强度Ms为31.5 kA/m，密度为2.1 g/cm3，工作温度范围为-60～150 ℃。因磁流体饱和磁化强度受温度影响较为严重，所以根据文献[21]在后续密封压力值计算时磁流体饱和磁化强度Ms取值为15 kA/m。

3 磁流体密封数值分析

3.1 数值分析过程

因密封间隙内磁感应强度受结构参数影响较大，而密封间隙取值较小，采用常规测量方法和计算很难得到间隙内磁感应强度，所以文中利用有限元计算软件COMSOL Multiphysics对所设计的磁流体密封组件密封间隙内磁感应强度进行数值计算及密封性能分析。由于磁流体密封组件为旋转轴中心轴对称结构，所以数值分析时将其简化为二维平面结构，如图5所示，相关尺寸如表1所示。根据表中尺寸且忽略非导磁结构的影响，建立数值分析模型如图6所示。

表1 磁流体密封组件尺寸

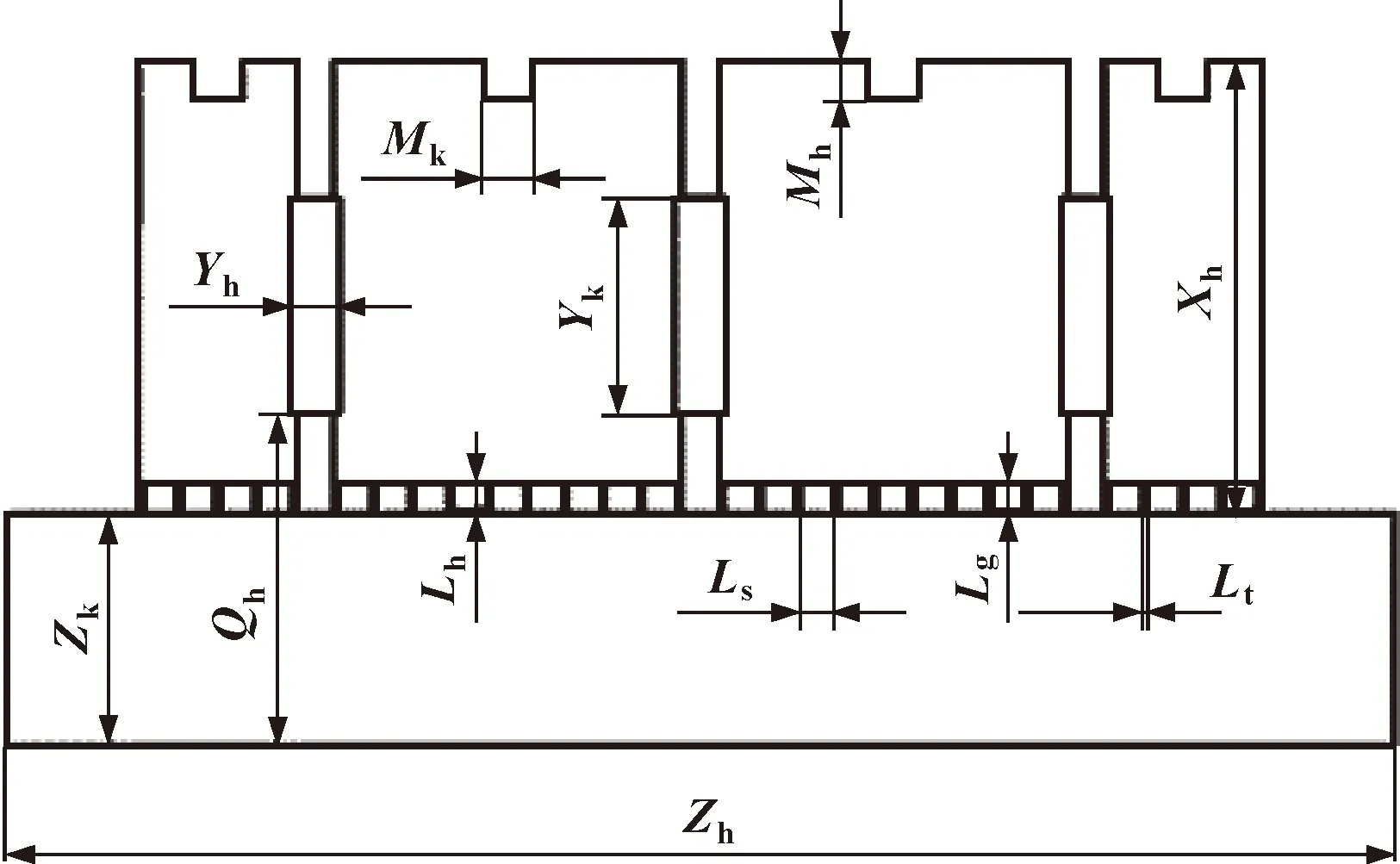
图5 磁流体密封结构

图6 仿真模型 图7 网格划分

根据磁流体密封组件材料选择对不同密封元件赋予相关材料，因磁流体磁导率与空气相近，所以采用空气代替磁流体。采用自由三角形对模型进行网格划分，并对密封间隙处进行网格加密处理，网格划分结果如图7所示。

网格划分完成后，添加边界条件，除模型中心对称轴Z轴以外，其余三条边界均设为磁绝缘边界，由于永磁铁为磁极性相同的面对面安装方式，所以中间永磁铁与两端永磁铁充磁方向相反，最后完成求解。

3.2 结果及分析

计算完成后得到磁流体密封装置磁感应强度、磁场强度分布，分别如图8和图9所示。利用软件后处理功能在密封间隙中间位置处沿轴向定义一条平行于转轴表面的直线，将密封间隙内磁感应强度大小及分布映射在此线上，如图10所示。

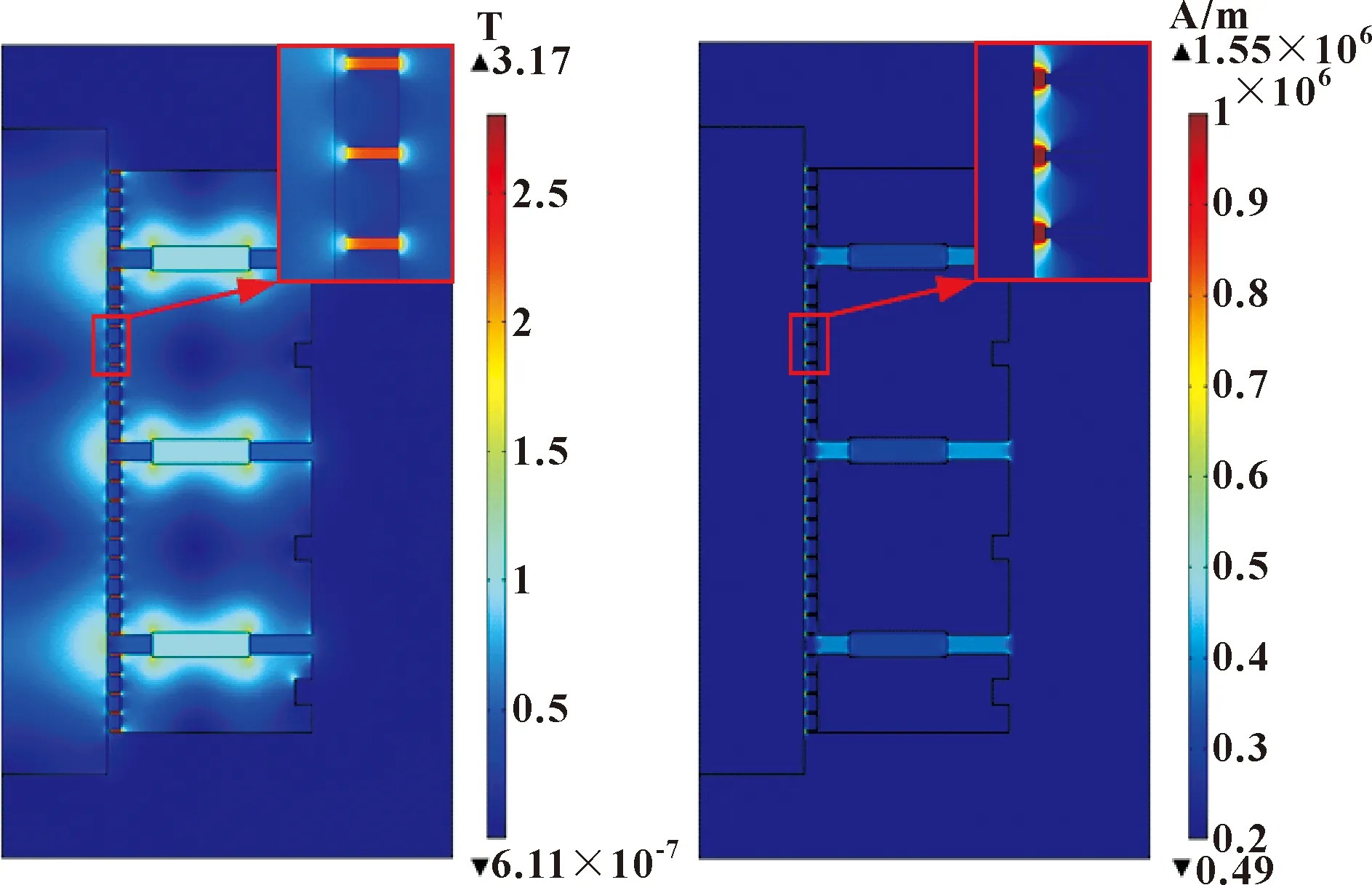
图8 磁感应强度分布 图9 磁场强度分布

图10 密封间隙内轴向磁感应强度分布

由图8和图9可知，磁流体密封装置极齿位置磁感应强度较强，并在密封间隙处发生磁场汇聚，形成磁场强度高位。由图10可得，在密封间隙中，极齿中间位置形成磁感应强度波峰，齿槽中间位置形成磁感应强度波谷，而磁流体密封耐压值与磁感应强度波峰波谷差值密切相关。通过计算得到磁流体密封理论压力值为0.266 MPa，虽说满足密封压力要求，但和工况压力较为接近，实际使用中容易发生密封失效，因此需对结构做优化处理。通过将以上磁流体密封组件仿真所得磁感应强度、磁场强度和密封间隙磁通密度分布规律与以上结果与文献[22-23]做对比，发现分布规律相同，证明数值计算模型及边界条件添加正确。

3.3 结构参数对密封性能的影响

为了分析不同结构参数对密封性能的影响并确定其取值范围，采用控制变量法和数值模拟分析方法相结合，计算了不同磁铁厚度(Yh)、宽度(Yk)，密封间隙(Lg)、极齿宽度(Lt)、极齿高度(Lh)、槽宽(Ls)和轴套厚度(Zh)参数下，极齿、密封间隙磁感应强度分布以及磁流体密封装置理论耐压值，结果如图11和图12所示。

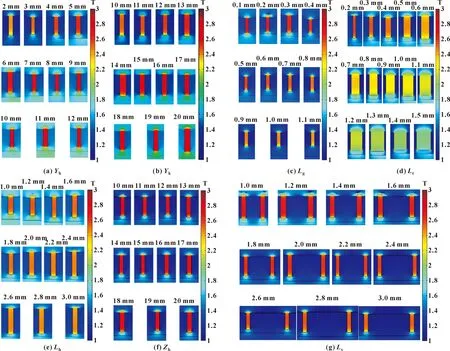
图11 结构参数对磁感应强度分布的影响

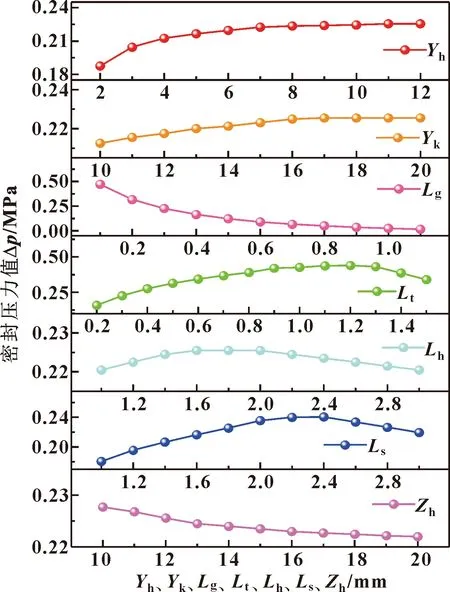
图12 结构参数对密封耐压值的影响

由图11(a)、(b)不难发现，随着永磁铁尺寸的增加，磁回路中磁能增加，密封间隙内磁感应强度差逐渐增加，密封压力值增加，当极齿达到饱和磁化强度时，磁阻增大，密封间隙内磁感应强度差值稳定，密封压力值也逐渐稳定。

由图11(c)可知，因空气磁阻较大，所以间隙越大，回路中磁阻越大，导致密封间隙内磁感应强度差变小，密封压力值降低。

由图11(d)可知，随着齿宽增大，极齿磁通路增加，磁阻减小，密封间隙内磁感应强度增加，密封压力值增加，而齿宽继续增加导致极齿下方空气占比增加，聚磁效果下降，密封间隙磁感应强度减小，密封压力值降低。

由图11(e)可知，随着齿高增加极齿聚磁效果增强，密封间隙中极齿和齿槽下磁感应强度差增大，密封压力值增加，而齿高持续增加极齿磁阻也增加，导致密封间隙中极齿下磁感应强度降低，密封压力值又开始降低。

由图11(f)可知，轴套厚度对密封间隙磁感应强度影响极小，而密封压力值降低主要是因轴套厚度增加所引发的离心力的影响增大导致的，所以文中在考虑轴承安装定位尺寸的情况下，取Zh为14 mm。

由图11(g)可知，随着槽宽增加，槽内磁感应强度降低，密封间隙内磁感应强度差增大，密封压力值增加，槽宽持续增加，槽内漏磁增加，磁感应强度差降低，密封压力值下降。

通过以上分析并结合图12可以看出，密封压力值随着永磁铁厚度(Yh)和永磁铁宽度(Yk)的增加，先增加后趋于平稳，随着密封间隙(Lg)和轴套厚度(Zh)的增加而降低，随着齿宽(Lt)、齿高(Lh)和槽宽(Ls)增加，先增加后减小。且各参数的取值范围分别是Yh≥7 mm、Yk=16～20 mm、Lg≤0.5 mm、Lt=0.9～1.3 mm、Lh=1.4～2.2 mm、Ls=1.8～2.6 mm，Zh=14 mm。

4 结构参数优化分析

4.1 正交试验

为提高所设计磁流体密封装置密封耐压性能，需综合多个结构参数对装置进行优化设计，而响应曲面优化法是一种通过较少的实验获得变量与响应面之间的关系及最优组合的优化方式[24-25]，因此文中将利用该方法对磁流体密封关键结构参数进行优化设计。

由于影响磁流体密封性能的结构参数较多，所以先利用正交试验确定对密封性能影响显著的因素作为响应曲面优化的设计变量。根据前文的分析结果，正交试验以密封间隙Lg、齿宽Lt、槽宽Ls、齿高Lh、磁铁轴向厚度Yh、永磁铁径向宽度Yk作为变量因素，分别以A、B、C、D、E、F代表以上变量因素，得到正交试验的因素水平表，如表2所示。根据表中变量因素个数及水平数，选用L25(56)正交表设计试验方案及分析，以密封压力值作为实验考核指标，并假设6个因素相互独立，互不干扰，计算结果如表3所示，表中A1代表A因素的第1个水平值，其余依次类推。

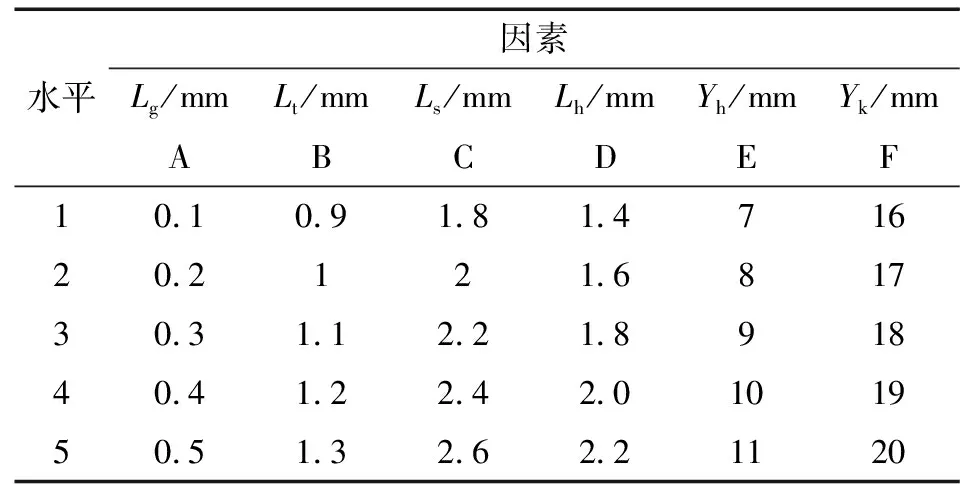
表2 正交试验因素水平表

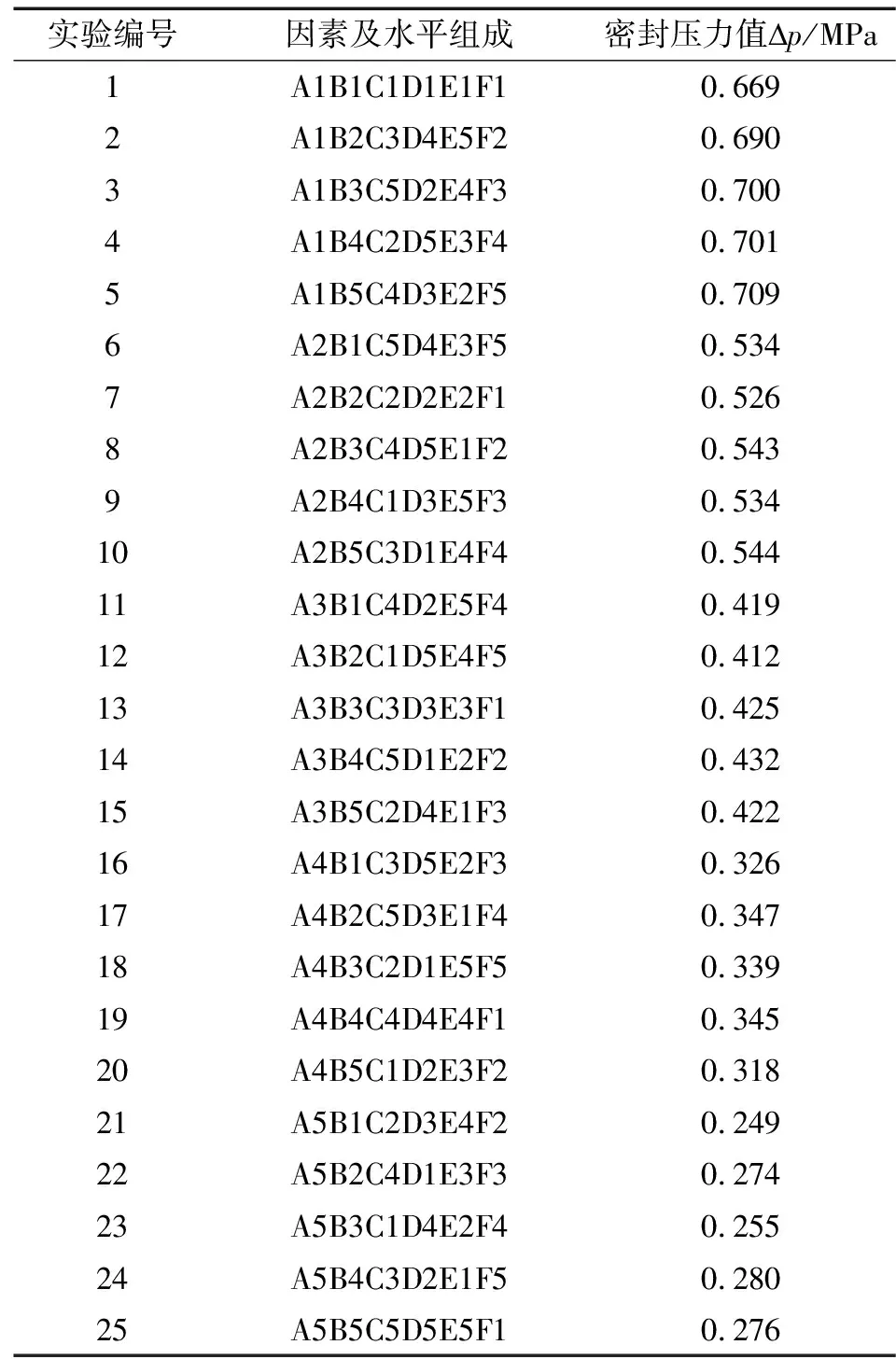
表3 正交试验结果

正交试验中极差分析可以快速得到各变量因素对考核指标影响程度，极差值R越大说明该因素对考核指标影响越大，反之则越小[26]。根据正交试验结果得到各因素极差计算结果，如表4所示。可得各参数对密封压力的影响程度依次为A>B>C>F>D>E，且A、B、C的影响程度远大于D、E、F。

表4 极差分析

4.2 响应曲面实验设计

基于正交试验结果及响应曲面优化法，以密封间隙A、齿宽B和槽宽C为设计变量，以密封压力Δp为响应目标对磁流体密封进行优化设计，将影响不显著的结构参数齿高、永磁铁厚度、永磁铁宽度分别取值为1.8、7和20 mm。

利用Design expert软件中的Box-Behnken实验设计方法进行实验分组，并通过有限元计算软件COMSOL Multiphysics对实验分组进行计算，结果如表5所示。

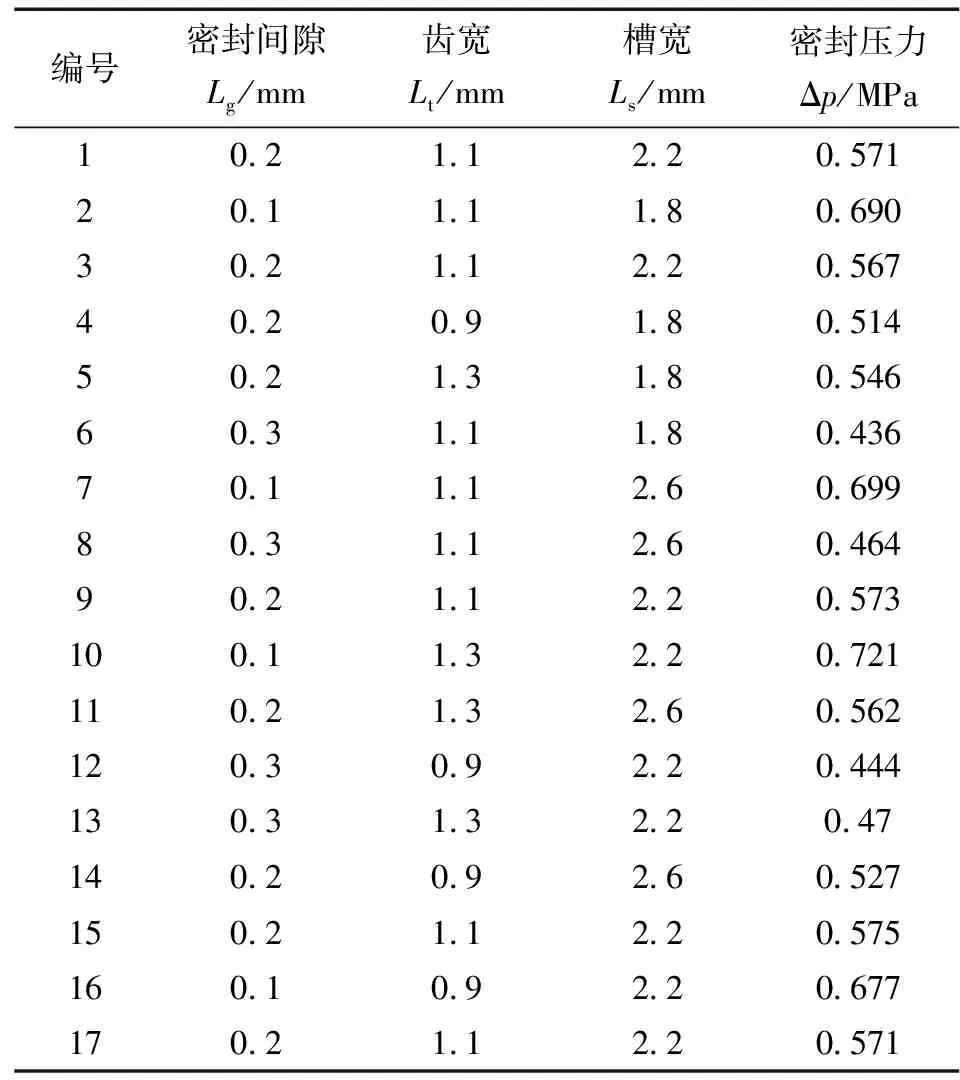
表5 Box-Behnken实验数据

通过对实验数据进行二次多元回归拟合，得到密封压力值的多元二次回归方程，如式(15)所示。

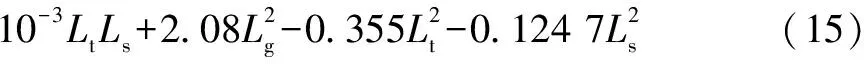
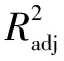
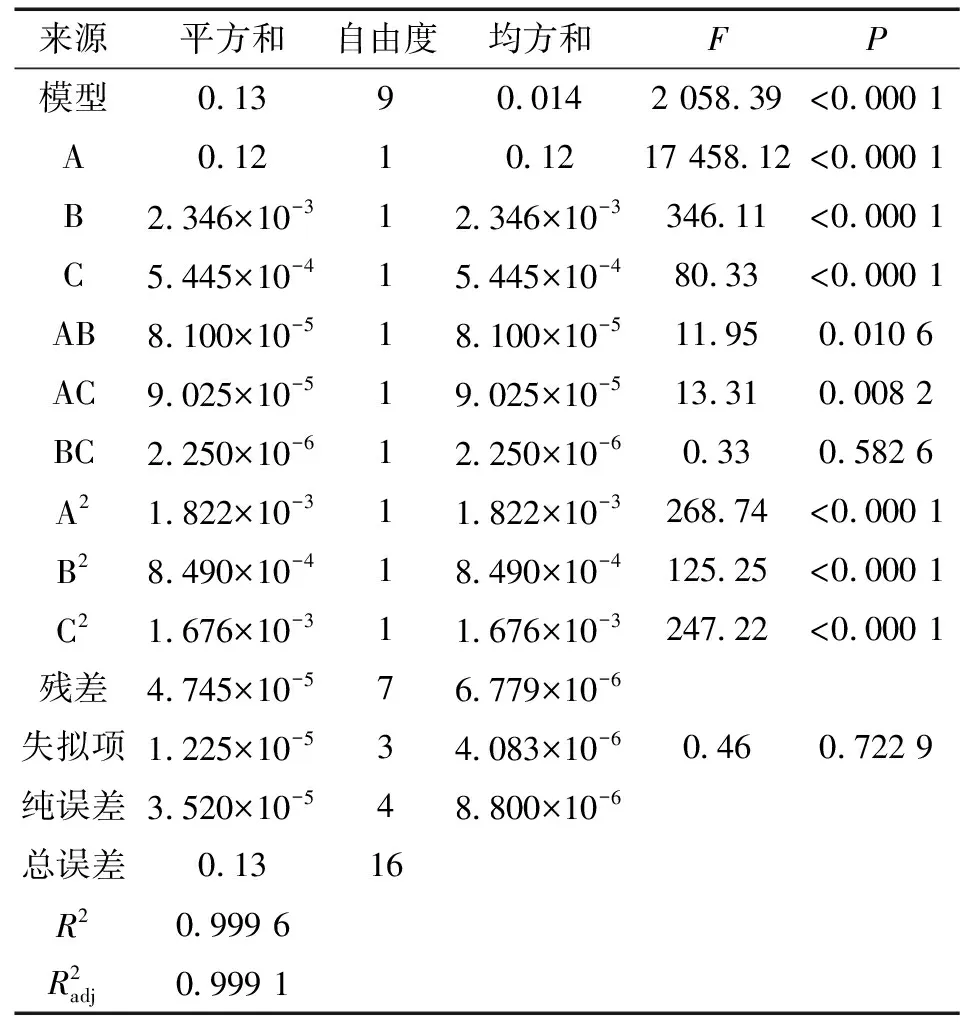
表6 方差分析

4.3 响应曲面结果分析

图13—15所示为密封间隙、齿宽和槽宽三结构参数交互作用的三维响应曲面图。从图13和图14可以看出，密封间隙分别与齿宽和槽宽的响应曲面存在明显“陡坡”，说明它们之间的相互作用对密封压力值影响显著。而图15中齿宽与槽宽的响应曲面较为“平坦”，说明其交互作用对密封压力值影响不显著。根据以上响应曲面结果可知，当密封间隙为0.1 mm，齿宽取值在1.1～1.3 mm，槽宽取值在2～2.4 mm范围内密封压力值取得较大值。

图13 密封间隙与齿宽对密封压力的响应曲面

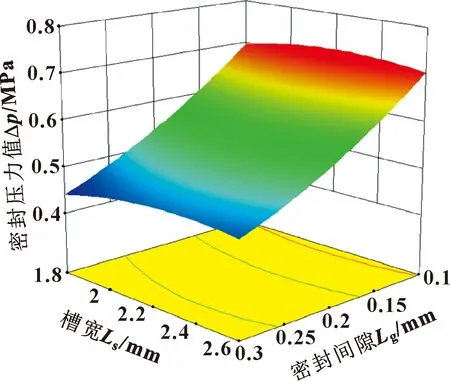
图14 密封间隙与槽宽对密封压力的响应曲面

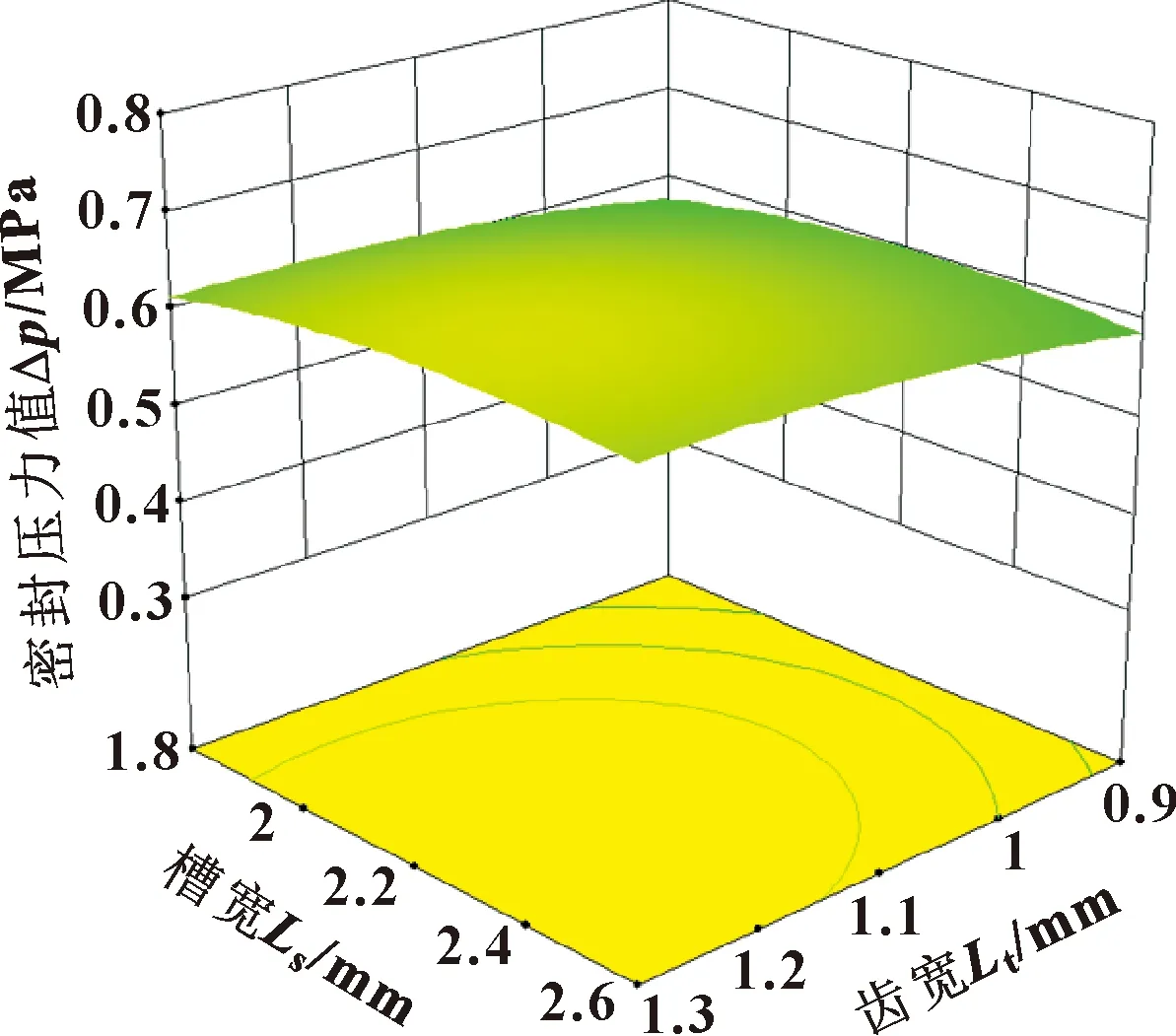
图15 槽宽与齿宽对密封压力的响应曲面

为确定最优结构参数取值，以最大密封压力值为优化目标，得到最终密封压力优化预测值及结构参数取值，并根据所得结构参数进行数值分析，得到密封间隙内磁感应强度分布，如图16所示。通过计算得到优化前后及预测密封压力值，如表7所示。优化后的计算结果与优化预测值存在一定误差，但误差小于5%，在允许范围内，且优化后的密封压力值0.721 MPa显著大于优化前的0.266 MPa和工况要求密封压力值0.26 MPa，证明优化有效并且磁流体密封装置满足设计要求。

表7 优化前后结果对比

图16 优化后密封间隙内磁感应强度分布

5 结论

(1)针对特定工况的离心压缩机，采用降温和降压结构，设计了一种多级并联磁流体密封装置；基于磁流体运动方程推导建立了考虑离心力影响的磁流体旋转动密封耐压计算公式，为离心压缩机磁流体密封的性能分析提供理论指导。

(2)当转轴线速度较高时，离心力对密封性能有显著影响；密封压力值随着永磁铁厚度(Yh)和永磁铁宽度(Yk)的增加，先增加后趋于平稳，随着密封间隙(Lg)和轴套厚度(Zh)的增加而降低，随着齿宽(Lt)、齿高(Lh)和槽宽(Ls)增加，先增加后减小。各参数取值范围：Yh≥7 mm，Yk为16～20 mm，Lg≤0.5 mm，Lt为0.9～1.3 mm，Lh为1.4～2.2 mm，Ls为1.8～2.6 mm，Zh为14 mm，为进一步结构优化了提供数据支持。

(3)利用正交试验分析法综合分析了结构参数对密封性能的影响，得到结构参数对密封能力影响程度：密封间隙>齿宽>槽宽>永磁铁宽度>齿高>永磁铁厚度。

(4)基于正交实验结果通过响应曲面优化方法对关键结构参数进行优化设计，当密封间隙为0.1 mm、极齿宽度为1.274 mm、齿高为1.8 mm、槽宽为2.236 mm、永磁铁厚度为7 mm、永磁铁宽度为20 mm时密封压力值为0.721 MPa，远高于工况使用要求，可有效解决离心压缩机密封困难的问题，也为高速旋转轴磁流体密封设计提供参考。