基于NS/CFIE 伴随方程的飞行器气动隐身综合优化

黄江涛，周琳，陈宪，*，马创，刘刚，高正红

1.中国空气动力研究与发展中心 空天技术研究所， 绵阳 621000

2.西北工业大学 航空学院， 西安 710072

未来先进作战飞机气动布局的重要发展方向为扁平化、高度融合，因此对气动隐身一体化设计技术提出了新的挑战，而先进气动布局设计技术是实现未来作战飞机高隐身、高机动、宽速域、远航程等技术指标的关键环节。近年来，在飞行器多目标、多学科优化上取得了丰硕的研究成果，尤其是高维设计变量、高维目标空间以及高保真度设计技术上取得了长足进展。但对于实际问题仍然存在以下瓶颈，限制了设计技术的工程实际应用：

1）气动外形精细化优化需求带来的学科分析精度的限制。工程分析方法一定程度上力不从心，尤其对于强非线性流动问题。例如，传统的面元法、速度势方程等在初步选型迭代、性能估算方面具有重要作用，但很难满足气动精细化阶段设计问题［1-3］。而另一方面，基于高可信度气动分析技术进行气动优化又导致了庞大的计算资源需求。

2）高频段的电磁散射设计导致的庞大计算量。高频段飞行器的隐身优化设计，带来设计变量空间维度较大，从而导致优化搜索量倍增；电磁计算网格规模庞大的问题，导致计算资源倍增，对于大尺度飞行器的气动外形设计与评估，即便是低频隐身设计，综合优化带来的高精度电磁计算量也是极为庞大的。

3）精细化/高可信度隐身设计需求导致的庞大计算量与内存资源需求。现有飞行器气动外形隐身设计研究中多采用几何光学法（GO）、物理光学法（PO）、几何绕射理论（GTD）、物理绕射理论（PTD）等高频近似算法，虽然计算速度快、所需内存小，但高频方法的理论模型粗糙，近似过程中会忽略一些关键部件间的重要电磁耦合关系，在处理包含大尺寸、小尺寸结构并存的复杂外形时精度较低［4-5］。

4）高维度设计变量、高可信度优化设计需求带来的优化算法、计算资源挑战。传统梯度寻优算法计算量正比于设计变量个数，进化算法所需种群规模与设计变量呈指数关系增长，导致计算量与资源需求呈指数增长；即使是采用响应面、Kriging、神经网络等模型［6-8］进行近似处理，仍然面临样本需求庞大、维度障碍、预测精度差等问题，在高维度设计变量问题中仍存在一定的短板。

由于多学科伴随体系［9-10］具有梯度计算量与各个学科设计变量个数均无关等优点，且通过耦合伴随方程的求解能够快速计算出各个学科关心的学科目标函数对所有设计变量的导数，倍受研究人员与工程师的关注与喜爱，同时也是国内外知名研发机构的重点发展方向［11-19］，必将在未来多学科优化领域发挥重要作用。针对作战飞机气动隐身一体化高可信度优化设计面临的上述难题，结合气动隐身多学科伴随方程构造以及灵敏度分析的优势，本文开展了基于NS（Navier-Stokes）/MLFMA（Multi-Level Fast Multipole Algorithm，多层快速多极子）方程及其离散伴随方程的飞行器气动隐身伴随优化设计技术研究，并针对低频雷达波环境气动隐身一体化设计进行了初步测试。

1 流场/电磁“耦合”伴随方程

首先，给出伴随方程基本形式：

式中：I 表示目标函数；W 表示状态变量；R 表示控制方程的残差；Λ 表示伴随变量。其中，伴随算子Λ 既可以是单学科伴随算子，也可以是多学科伴随算子［9］，对应的残差同样也可以是多学科约束，采用相同方式进行伴随方程推导，可以得到多学科耦合伴随方程。采用式（1）向量求导形式可以直接推导出流场/电磁“耦合”伴随方程：

式中：Ra、RE分别代表流场残差与电磁数值计算残差；wi、Aj分别代表流 场 变 量 与电流分布；I 为表面感应电流。显然式（2）交叉导数雅克比矩阵为0，即：

“耦合”伴随方程退化为

从式（4）可以看出，气动电磁多学科伴随方程完全解耦，不存在耦合，这对研发体系来讲难度大大降低，2 个伴随方程完全独立求解。基于高可信度流场电磁伴随优化的方面的研究从发表文献上看几乎是空白。一个主要原因是学科跨度较大，变分困难，计算量庞大。在流场伴随与电磁伴随优化基础上，本文基于矩量法构建了气动隐身高可信度优化系统［20］，为气动隐身综合优化设计奠定了技术基础［9，21］，在此基础之上将电磁伴随方程推广至多层快速多极子算法，大幅提高在工程使用中效率与可行性，提升工程设计中的应用频段范围。

2 基于NS 的流场伴随方程

基于NS 的离散伴随方程对的构造主要依赖于空间离散格式、插值精度、边界条件处理方式的选择，不同的空间离散格式以及插值精度会产生不同的模板需求，尤其对于高精度格式来讲，其无黏项的离散伴随构造将及其复杂。空间离散方法采用二阶精度的中心格式，该格式构造简单，在亚、跨、超声速流场数值模拟中表现鲁棒，在实际工程应用较多［22］。

将上述结果进行整合，并加入伪时间项可以得到离散伴随主控方程：

式中：V 为电磁激励。对式（6）的迭代求解，可以采用显式经典四步龙格-库塔推进，也可以采用隐式时间推进。由于式（6）在形式上与NS 方程一致， LU-SGS 方法及其最大特征值分裂方法可以用于离散伴随求解，因此，本文采用LU-SGS时间推进方法。流场时间推进采用的隐式边界条件在离散伴随方程中依然可用：

3 基于MLFMA算法的混合场积分伴随方程

在电磁散射计算中，由于混合场积分方程（Combined Field Integral Equation，CFIE）可以避免电场积分方程（Electric Field Integral Equation，EFIE）和磁场积分方程（Magnetic Field Integral Equation，MFIE）存在的“内谐振”问题，同时具有较好的条件数，且鲁棒性较好，因此，在封闭外形的电磁散射计算中通常采用多层快速多极子方法求解CFIE 方程，基于电磁场表面积分方程的RCS 求解方法，电磁散射最优化问题可以表示为

结合式（1）可得隐身问题对应的伴随方程：

相对于有限差分计算来讲，基于矩量法的电磁伴随求解将灵敏度计算效率提高2 个量级以上，且随着入射频率的增加，加速效果更加明显。然而，矩量法伴随方程面临两个问题：阻抗矩阵存储空间瓶颈、几何扰动进行阻抗矩阵装配时间消耗。两方面因素较大程度限制了电磁伴随优化在大尺度特征飞行器、复杂气动构型问题中的应用。

针对该问题本文基于多层快速多极子算法开展伴随方程构造以及梯度计算研究。对于磁场积分方程和混合场积分方程，由于MFIE 和CFIE 阻抗矩阵与其转置并不相等，因此无法直接建立伴随变量与正计算结果的关系。多层快速多极子算法计算远相互作用矩阵与相应元素电流的矢量乘ZfarI，在远相互作用矢量乘的计算过程中不显式存储Zfar，无法通过改变Z 的索引方向对多层快速多极子的阻抗矩阵进行转置运算，同时多层快速多极子算法采用广义极小残差法（General Minimum Residual Method，GMRES）迭代法对离散方程进行求解，因此伴随方程求解的核心在于计算ZTI，具体计算分为近场矢量乘和远场矢量乘两部分。

近场矢量乘计算在最细层进行，在并行多层快速多极子算法框架下附近组元素按照块状分布，在存储中仅需要保存每一块的起始行号、起始列号、行数和这一块中所有附近元素即可；在近场并行计算中将基函数分配到不同进程进行计算和存储，在正计算中通常采用按行分配的方式，显然，由于转置原因，在伴随计算中应采取按列分配的方式，确保同一列的元素保存在同一进程，伴随计算的近场矩阵乘可以写为伴随计算的远场矢量相乘与正计算的较为相似，但在计算顺序和波的传播方向上与正计算有所区别。伴随计算远相互作用矢量乘的需要在相乘的过程中交换场、源点的位置，伴随计算远相互作用的矢量乘可以表示为

注意到在进行伴随矩阵乘时，首先计算电流Ii与配置因子的乘积；转移时转移因子为αm′m与正计算的αmm′方向相反。式（11）中Ii为第i 个源 点 的 电 流 幅 度，Vfmj、αmm′和Vsm′i分 别 表 示 配置、转移和聚合因子，*表示共轭运算，伴随方程中配置、转移和聚合因子表达式与正计算问题基本一致，归纳伴随计算与正向计算的几个细节差异：

3）多极配置过程，伴随计算中多极配置中使用e-ik(l-1)n′rmlml-1将聚合量从父组中心转移到子组中心，在正计算中使用eik(l-1)n′rmlml-1进行转移计算。

绿色高等植物都是由很多细胞组成的，植物受冻实际上就是某个部位的细胞受冻。一般地，处于休眠状态的植物细胞早就做好了耐冻的准备，从夏天就开始逐渐脱水，冬天芽细胞断开与维管束之间的联接，处于最低含水量状态，不做任何新陈代谢活动，细胞原生质内存储的蛋白质、糖和淀粉等高分子物质使细胞质溶液保持一个最低的结冰温度数值 （也就是冰点温度），这样就保证细胞质在0℃以下的环境中也不会结冰。当气温下降到细胞难以抵挡的时候，植物还有最后一招，那就是首先在细胞之间结冰，这样，如果低温很快就过去，那么细胞间的冰晶就会逐渐融化而不会伤及细胞内，使果树遭受最小的伤害。

上述计算过程的表达式及其具体含义是计算电磁学中的常见要素，具体可参考文献［23-24］，这里不再赘述。

至此，伴随方程左端项推导已经完成，进一步我们需要解决右端项变分。伴随方程（10）的右端项激励∂σ ∂I 为雷达散射截面关于感应电流的导数，现就∂σ ∂I 的计算方法进行推导。求解得到表面感应电流分布后可以通过式（13）求得RCS：

式中：上划线-表示共轭。由链式求导法则：

复数求导需分别对其实部和虚部求导，即：

则式（16）可以整理为

式（15）中g 离散后可以写成感应电流和的形式，以RWG 基函数为例写出g 的具体表达式：

式中：In为第n 条边上基函数的权重，推导得到∂g ∂In和∂gˉ∂In的表达式：

从上述过程容易看出，电场积分伴随方程是自我伴随方程，而混合场积分伴随方程的自我伴随特性消失。通过伴随方程求解得到Λ 后，根据式（21）可将伴随梯度表示为

需要指出的是，在依据式（21）进行梯度计算的过程中，由于扰动外形的底层盒子分布与初始外形可能存在差异，导致基函数的局部编号也会有所不同，因此在存储正计算电流和伴随计算电流的时候需根据基函数的全局编号或面元的全局编号进行存储。

4 飞行器气动/隐身综合优化设计体系

基于上述伴随体系的构建，结合参数化建模模块、SQP 寻优算法以及网格变形技术［25］，本文建立了基于跨学科伴随体系的飞行器气动隐身综合优化平台AR3Design。图1 给出了建立的飞行器气动隐身综合优化平台的工作流程图。在优化过程中，参数化建模运算建立表面网格和设计变量之间的映射，通过寻优过程，得到新的设计变量，进而得到新几何外形的表面网格。网格变形技术基于新的表面网格，采用径向基函数（Radial Basis Function，RBF）-无限插值（Transfinite Interpolation，TFI）网格变形技术［25］得到新外形的空间网格，之后再进行新一轮计算，直至优化过程收敛。

图1 飞行器气动隐身综合优化流程图Fig.1 Flowchart of integrated aircraft aerodynamic stealth optimization

5 飞翼布局气动隐身综合设计

本文采用的类X47B 外形作为研究对象，其几何特征如图2 所示，基础布局翼根采用反弯翼型、外翼段超临界翼型生成。布局的参考面积为42.43 m2，重心位置为(xg，yg，zg)=(6.77，0，0) m，平均气动弦长3.32 m。设计状态：Ma=0.76， H=13 km，CL=0.36， Re=1.396×107。

图2 几何特征与电磁入射坐标定义Fig.2 Geometric features and definition of electromagnetic incident coordinates

隐身评估考虑f=200，500 MHz 这2 个频点，采用垂直极化（VV），考虑方位角φ=0°～60°、θ=-10°～10°的RCS 均值，图2 给出了方位角定义示意图；该型飞翼布局参数化采用基于NURBS基 函 数 的FFD 进 行 参 数 化 建 模［26-27］，如 图3所示。

图3 飞翼布局FFD 参数化Fig.3 FFD parameterization of flying wing configuration

几何约束考虑展向均匀分布的20 个剖面，要求各剖面外形的最大厚度不减小、容积不低于初始外形的95%。CFD 计算采用多块对接结构网格，采用k-ω 剪切应力输运（Shear Stress Transport， SST）湍流模型；隐身计算采用非结构表面网格，网格平均边长Δx=0.1λ，在几何变化剧烈的地方进行加密。开展在f=200，500 MHz 的气动/隐身优化，验证跨学科伴随优化的有效性，分别记为Aero-RCS optimization 200M、Aero-RCS optimization 500M，采用加权的方式耦合气动、隐身的设计目标，气动隐身优化的数学模型为

初始外形的表面压力分布如图4 所示，其中阻力系数CD=138.7 counts、力矩系数Cm=0.020 4。初始外形在f=500，200 MHz 的RCS 均值分别为。

图4 初始外形压力云图Fig.4 Pressure contour of initial configuration

优化过程采用160 个设计变量，分别在f=500， 200 MHz 这2 种不同雷达频率下进行综合优化，相应的收敛曲线分别如图5 和图6 所示。优化采用64 核心进行，总耗时30 h。因此，利用小型工作站即可开展基于伴随方法的飞行器全机气动隐身综合优化。前人的研究结果也表明［21，28］，基于伴随方程的气动隐身优化方法具有高效、高精度的优点，伴随方法计算得到的梯度与有限差分法高度一致，并且伴随方法的效率是有限差分法的数10 倍。

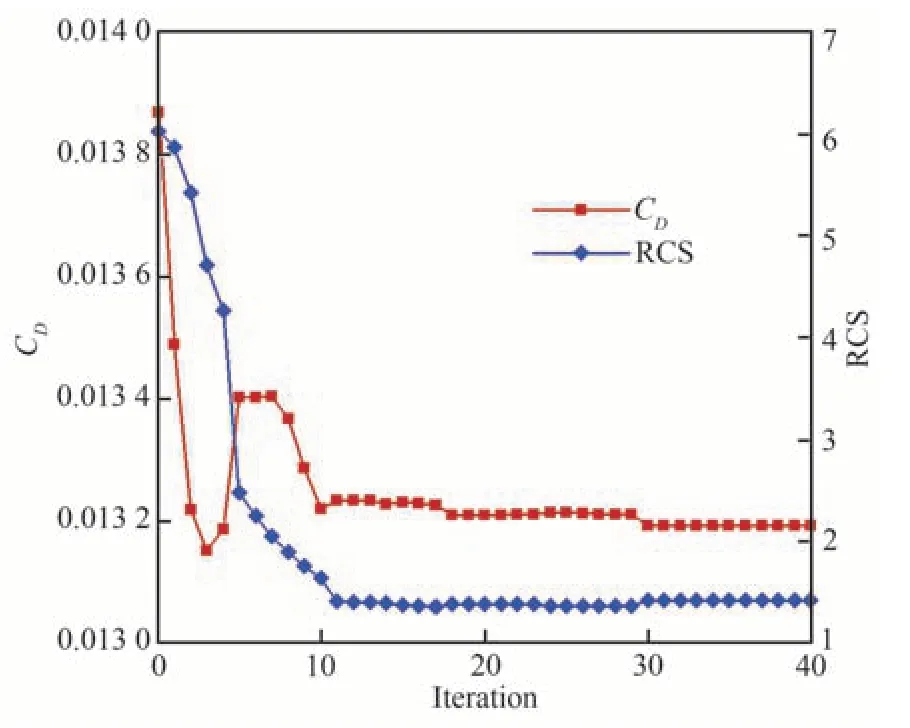
图5 气动隐身综合优化历程（200 MHz）Fig.5 Aerodynamic stealth optimization process （200 MHz）

图6 气动隐身综合优化历程（500 MHz）Fig.6 Aerodynamic stealth optimization process （500 MHz）

伴随优化前后气动隐身特性对比如表1 所示，在本文算例中力矩没有作为目标或约束进行处理，可以看出由于权重的设置以及隐身梯度的量级较大，使得RCS 单调下降，阻力呈现一定的振荡。

表1 伴随优化前后气动隐身对比Table 1 Comparison of aerodynamic stealth before and after optimization

气动隐身优化外形的表面压力云图如图7 和图8 所示。可以看到，不同频段的综合优化结果上表面激波强度明显低于初始外形，接近无激波状态；RCS 也实现了大幅度下降，验证了本文建立的基于NS/CFIE 伴随方程气动隐身优化方法的有效性。

图7 优化外形压力分布云图（200 MHz）Fig.7 Pressure contour of optimized configuration（200 MHz）

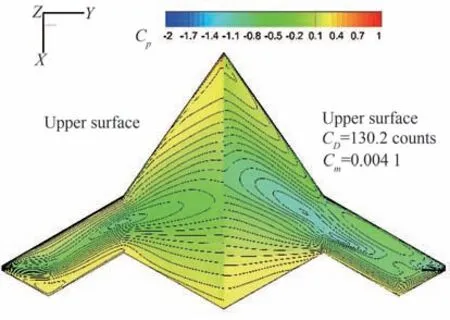
图8 优化外形压力分布云图（500 MHz）Fig.8 Pressure contour of optimized configuration（500 MHz）

初始、Aero-RCS optimization 200M、Aero-RCS optimization 500M 外 形 在 翼 根（Y=0.2 m）、kink1（Y=4.5 m）、kink2（Y=8.0 m）剖面的几何及压力分布对比如图9～图11 所示。由于中央体是主要雷达散射源，在中央体附近的剖面几何外形和压力分布形态发生显著变化，各个频率优化的前缘半径明显减小，且呈现“鹰嘴”型；在Y=4.5 m 剖面和Y=8.0 m 剖面，前缘半径均小于初始外形，但减小程度弱于Y=0.2 m；剖面负扭转角度以及后加载明显增加，2 种优化工况载荷分布更加接近椭圆，如图12所示。

图9 展向Y=0.2 m 优化前后对比Fig.9 Spanwise Y = 0.2 m before and after optimization

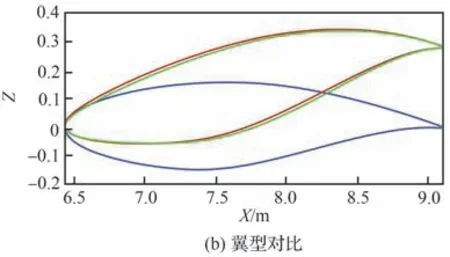
图10 展向Y=4.5 m 优化前后对比Fig.10 Spanwise Y=4.5 m before and after optimization

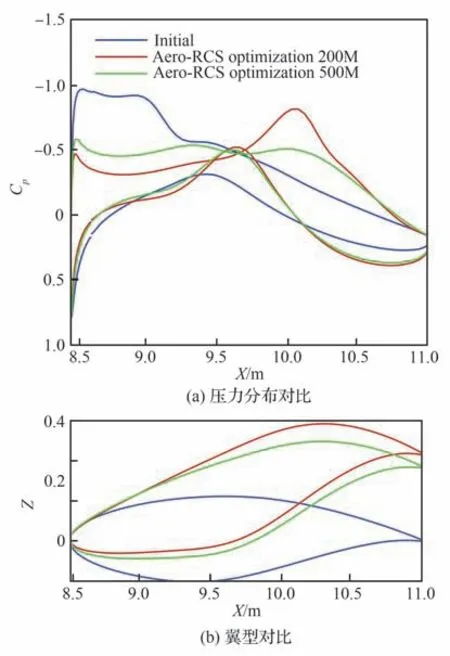
图11 展向Y=8.0 m 优化前后对比Fig.11 Spanwise Y=8.0 m before and after optimization

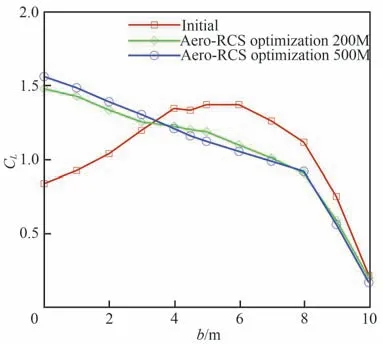
图12 优化前后展向载荷分布对比Fig.12 Comparison of spanwise load distribution before and after optimization

气动隐身优化外形优化前后，在f=200，500 MHz 的水平、垂直RCS 评估结果如图13～图16 所示，评估时固定φ=0°。对于垂直极化，在f=200， 500 MHz 的RCS 减缩效果非常显著，在φ=0°～60°范围内的RCS 均明显降低，其中φ=55°峰值（大尺度中央体的贡献）的高度明显降低，φ=30°峰值高度略有降低。对于水平极化（HH），由于水平极化的RCS 主要受外形在x-y平面的几何特征影响，剖面形状优化虽然可以降低边缘在水平极化的散射强度，但对水平极化入射时目标的整体RCS 特征影响不显著，优化后外形的RCS 略有降低，但降低幅度明显小于垂直极化。

图13 初始与优化外形RCS 对比（f=200 MHz，VV）Fig.13 RCS comparison between initial and optimized configurations （f = 200 MHz， VV）

图14 初始与优化外形RCS 对比（f=200 MHz，HH）Fig.14 RCS comparison between initial and optimized configurations （f = 200 MHz， HH）

图15 初始与优化外形RCS 对比（f=500 MHz，VV）Fig.15 RCS comparison between initial and optimized configurations （f = 500 MHz， VV）

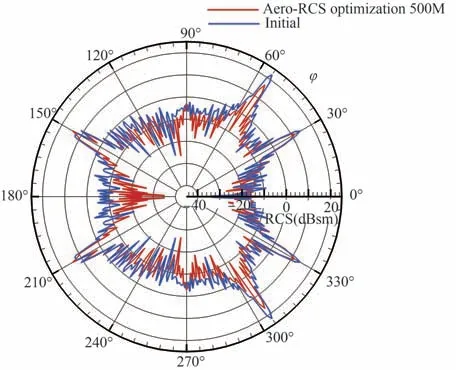
图16 初始与优化外形RCS 对比（f=500 MHz，HH）Fig.16 RCS comparison between initial and optimized configurations （f = 500 MHz， VV）

对于目标在较低频率的散射问题，不同散射源间的相位对总RCS 具有显著影响。考虑相位影响时，通常采用量化RCS，其 中为 复数，定义如式（23）所示：

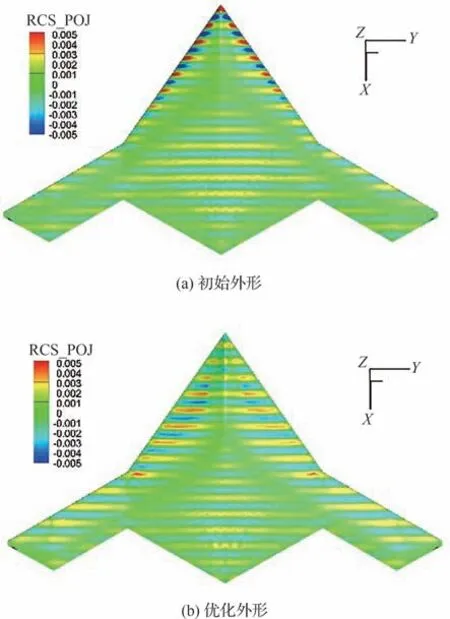
图17 初始及优化外形表面散射贡献（f=200 MHz）Fig.17 Surface scattering contribution of initial and optimized shapes （f= 200 MHz）

图18 初始外形及优化外形表面散射贡献（f=500 MHz）Fig.18 Surface scattering contribution of initial and optimized shapes （f= 500 MHz）

可以看到，对于f=200 MHz，面元对总RCS 的贡献受相位影响显著，贡献量正负交替，间隔为半波长，全机各位置均对总RCS 有显著影响。当f=500 MHz 时，贡献量随也呈现正负变化特征，但主要RCS 贡献区域集中在布局前缘，局部特性更加显著。对比优化前后外形，相对于初始外形，优化外形的前缘的贡献明显降低，其他区域的贡献变化趋势不明显，甚至局部略有增加。

6 结 论

基于NS 方程以及MLFMA 算法的CFIE 方程构造了气动隐身伴随方程，并进一步进行气动隐身综合优化测试：

1）流场电磁多学科伴随方程完全解耦，不存在耦合，2 个学科的离散伴随方程可以完全独立求解。

2）雷达散射伴随计算与正向计算在多极聚合、多极转移、多极配置以及部分场展开过程存在差异，主要体现在波方向、转移因子等方面。

3）剖面的优化对气动性能、垂直极化隐身效果较为明显，剖面形状优化虽然可以降低边缘在水平极化的散射强度，但对水平极化入射时目标的整体RCS 特征影响较垂直极化弱。

4）飞翼布局测试算例表明，本文建立的基于NS 方程以及MLFMA 算法的气动隐身优化方法具有极高的优化效率以及设计效果。

本文对低频入射波条件的气动隐身伴随优化设计进行了研究，仅从方法角度验证了气动隐身伴随方程构造的可靠性与有效性。由于AR3Design 平台采用多层快速多极子算法、NS方程分别作为隐身、流场伴随方程构造的基础，因此，该伴随优化体系具有全频段、宽速域设计能力，基于AR3Design 开展飞行器宽频段、宽速域、多约束气动隐身综合优化设计研究是本文将进一步开展的工作。