高超声速平板边界层中波纹粗糙壁峰值热流的变化规律及预测

孔祥志，韩宇峰*

天津大学 高速空气动力学研究室，天津 300072

一直以来，气动加热在高超声速飞行器的设计中占据着关键的地位，是工程实际及理论研究都关注的问题。飞行器表面的热防护材料在经过烧蚀后，会发生一定程度的变形，形成粗糙表面，对流动和气动加热产生不可忽略的影响。

在实际问题中，粗糙壁面形式多样，开展对粗糙壁面峰值热流特性的研究，首先要建立描述粗 糙 壁 面 特 征 的 模 型。Colebrook 和White［1］的研究发现，粗糙密度对于表征粗糙特征是至关重要的，后来Schlichting［2］量化表征了粗糙密度，用λ=Fr/F 定义粗糙密度，Fr表示粗糙壁正面总投影面积，F 表示粗糙与壁面平行的投影面积；Nikuradse［3］基于粗糙密度提出等效砂砾高度的概念，通过试验建立起等效沙砾高度与粗糙壁面特征的关系；Sigal 和Danberg［4］扩展 并改进了这一映射关系，使用Sigal-Danberg 参数定义了粗糙密度，使等效砂砾高度获得更为广泛的应用。此外，为了表征粗糙壁面特征，Napoli 等［5］提出有效斜率的概念衡量粗糙壁面的高度及密度，用于对完全粗糙壁面特征的表征，同时研究了有效斜率与粗糙壁面摩阻和热流的关系。上述粗糙特征模型由于提出角度的不同，适用于不同壁面粗糙情况［6］。

对于高超声速粗糙壁的气动热规律，从20 世纪70 年代以来开展了大量的实验研究。Bertran等［7］在Jaeck［8］的试验报告基础上，研究平板波纹型粗糙壁的传热特性，重点研究第1 波峰值热流的演变规律，发现了粗糙高度、宽度、间隔等对于热流的影响规律；美国PANT 计划、文献［8-14］利用实验得到的数据，拟合得到若干计算粗糙壁面热流的经验预测公式，受限于实验数据以及实验条件，这些公式不具有很大的通用性；Nestler［15］综述了表面粗糙对传热影响的实验数据以及预测方法，这些表面粗糙的类型包括台阶、空穴、间隙和突起等，通过对该领域关键技术的评估，指出以往对于粗糙壁气动热特性的研究缺乏对传热过程的物理认知，建立的经验相关性公式是不充分的，需要更完善的实验数据以及新的预测方法。

除了实验，学者们也采用各种数值方法对高超声速粗糙壁的热流进行了研究。Polak 等［16］使用隐式有限差分技术研究不同马赫数、雷诺数下的波纹型粗糙壁面的热流演变规律，并对Jaeck等［8］提出的峰值热流预测公式进行评估，发现预测公式对试验结果存在严重依赖；Egorov 等［17］数值研究波纹粗糙平板壁面，得出壁面热流的变化规律，指出在粗糙壁面峰值附近，热流会达到最大；李俊红等［18］用数值模拟和理论方法对高超声速可压缩湍流中的粗糙壁面热增量进行研究，讨论了不同粗糙高度、密度等对热流的影响规律，比较了几种预测公式［12-14］的结果与数值结果的差异；李玉川和鲍麟［19］研究波纹粗糙壁面上高速气流的流动和传热特性，结果表明在波状壁流动中，壁面热流系数与总阻力系数呈现出直接关联。Kumar 和Reddy［20］在 平 板上布 置 三 维 凸起，通过实验研究凸起附近的热流，使用不同工况下的实验数据拟合得到用于预测凸起附近热流的关系式；Estruch-Samper［21］在平板上布置短压缩斜坡粗糙元，研究粗糙偏转角对于峰值热流等的影响，评估几种峰值热流预测公式的有限适用性；Avallone 等［22］通过实验研究圆柱形粗糙元的流动以及热流峰值特征；Thakkar 等［23］使用多组不规则粗糙表面的模拟数据，开发了具有多个参数的粗糙壁面特征优化模型，但是这一模型的参数较多，实际使用起来较为复杂。

总之，目前对于粗糙壁面的气动热有了深入的认知，但多数研究集中在再入飞行背景下的大尺度（毫米-厘米量级）烧蚀。随着新型航天航空飞行器的发展以及其表面精细化的热防护需求，复合烧蚀材料由于轻量以及高密度等优势，应用越来越广泛，相比于传统烧蚀材料，复合烧蚀材料的线烧蚀率更低。例如在10～12 马赫数范围的高超声速巡航或滑翔飞行器上，机翼结构采用瓦状非承重外部隔热系统，对于低重量的隔热瓦，会产生百微米量级的波纹型表面粗糙［24］。毫米以下的微粗糙和毫米、厘米量级的大粗糙的流场结构是有显著差异的。微粗糙尺度远小于边界层厚度的，流场结构较为简单，壁面热流增量主要是由于壁面剪切耗散增大而导致［16］；大粗糙尺度与边界层厚度相当，流场结构更为复杂，粗糙附近压力波动较大并出现流动分离，热流会受分离涡影响，热增量机理更为复杂。目前已有的预测方法，都是针对大粗糙壁的基于实验拟合得到的半经验平均热流预测公式。对于微粗糙度的峰值热流，这些方法是不适用的。此外在这种微烧蚀情况下的粗糙壁面峰值热流的预测是很稀缺的［16］。

在实际中，飞行器表面因烧蚀而产生的粗糙形状是复杂的，但是等效砂砾粗糙度概念的提出启示我们可以利用一种标准粗糙元模型等效地模拟实际粗糙壁面形状以获得壁面热流变化的规律。

本文重点关注微烧蚀条件下出现的百微米量级的波纹型粗糙壁，结合目前对于粗糙壁热流影响因素的认识以及预测方法，使用直接数值模拟计算不同高度、流动参数下的流场及热流。在此基础上，进行理论分析，总结数值结果的规律，提出定量预测粗糙壁面峰值热流的模型。

1 物理模型及数值方法

1. 1 控制方程

通过直接数值求解直角坐标系下的可压缩守恒型Navier-Stokes（N-S）方程获得平板边界层的流场，其控制方程为

式中：t 为时间变量；x、y 分别为流向和法向的空间坐标；U 为守恒型变量；E、F 分别为流向、法向的通量；Ev、Fv为相应的黏性项，各项的具体表达式分别为

其中：u、v 分别为流向、法向的速度分量；p、ρ 和T分别表示压力、密度和温度；μ 为黏性系数；κ 为热传导系数；黏性系数使用Sutherland 公式计算：

式中：Tμ为参考温度，取110.4 K。

热传导系数在普朗特数以及定压比热为常数的条件下与黏性系数为线性关系：

式中：Tκ为参考温度，取110.4 K。

在计算过程中需要选择适当的特征尺度对方程进行无量纲化。上标*号表示有量纲物理量，无上标*号的量表示无量纲物理量。选取特征长度L*对空间坐标进行无量纲化：

雷诺数、马赫数分别为

无量纲形式的黏性系数和热传导系数分别为

1. 2 数值格式和程序验证

壁面采用无滑移边界条件，上边界给定来流条件，入口采用自由来流条件，出口采用线性外推。采用基于有限差分的直接数值模拟方法开展流场计算，计算对流项采用三阶WENO（Weighted Essentially Non-Oscillatory）格式，黏性项采用四阶中心格式，通量分裂选择Steger-Warming 分裂，采用四阶龙格-库塔方法在时间方向推进求解。

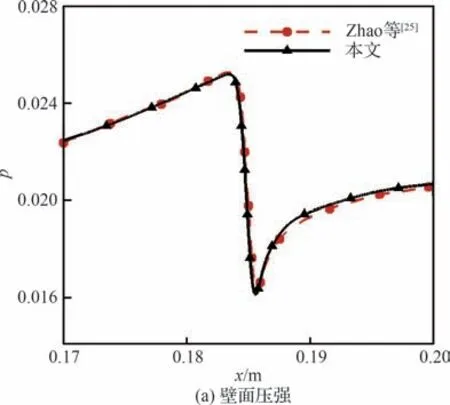
为了验证数值程序的正确性，与Zhao 等［25］关于单个正弦粗糙元的高超声速流动研究中的工况进行比对，图1 展示了流场的壁面压强分布和粗糙元附近的速度剖面的对比结果，可以看到，在粗糙元附近，计算结果基本吻合，验证了所使用程序在计算粗糙元时的正确性。

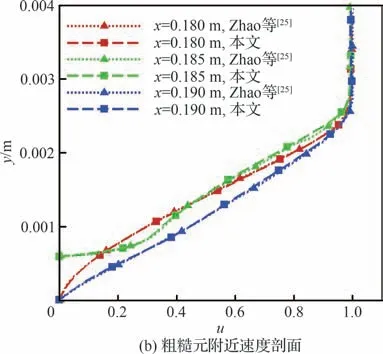
图1 程序验证Fig.1 Program verification

1. 3 物理模型、网格划分策略及计算参数

数值模拟的物理模型为全场均布正弦型波纹的平板，如图2（a）所示，壁面连续分布有100 个周期的正弦凸起。壁面函数表达式为

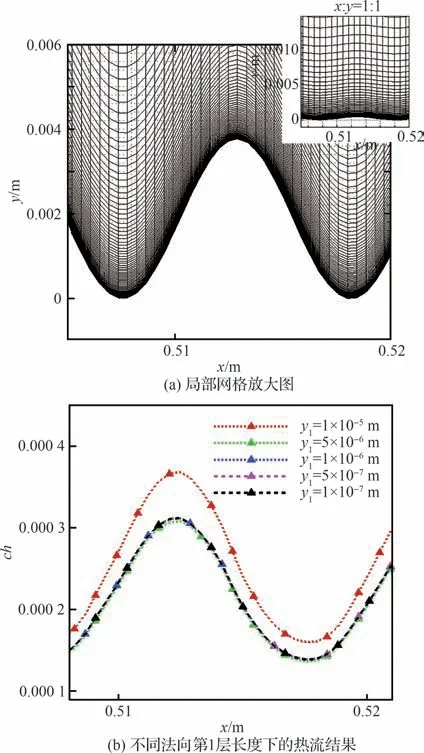
图2 正弦型壁面粗糙分布及热流验证Fig.2 Sinusoidal wall roughness distribution and heat flux verification

式中：h0、kn和L 分别为粗糙元的高度、个数和宽度。近壁面使用贴体网格。同时为了使粗糙元以外的部分不受到网格弯曲带来的影响，在距离粗糙元一定高度以上，仍采用平行网格，二者光滑过渡；为了准确计算热流，法向网格尺度使用基于分子平均自由程的网格准则［26-27］得到，法向第1 层网格尺度在10-6m。在每个粗糙单元尺度上流向分布20 多个点，法向分布100 多个点，计算域总网格量为100 万左右，具体网格分布如图2（a）所示，图中右上角为x、y 坐标比例为1 的示意图。不同法向第1 层长度（10-7～10-5m）下热流的计算结果见图2（b），图中y1表示法向第1 层网格长度，可以看出，10-5m 的结果偏差很大，5×10-6m 的结果趋于收敛，但仍有细微的偏差。而在长度为10-6、5×10-7、10-7m 时，热流结果完全一致，说明在法向第1 层网格尺度10-6m下可保证热流的计算是准确的。后文计算中每个算例都经过了网格无关性检验，以保证计算结果的准确性。

使用无量纲的热流系数ch 来表征壁面热流：

式中：chsm表示对应光滑壁的热流系数；计算的来流参数选自30 km 的大气，特征长度选取1 m，具体参数见表1。

表1 计算参数Table 1 Calculation parameters

2 数值结果及分析

粗糙壁的几何特性会影响壁面热流的演变规律，Sigal［4］、Bertram［7］、Polak［16］、李俊红［18］等对粗糙壁高度、宽度、形状等几何特征对壁面热流的影响进行了研究，结果表明，高度和宽度是较为关键的影响因素，两者通常以比值形式的关系［4］体现这种影响规律。

为了研究不同几何特征以及来流参数对于粗糙壁峰值热流的影响规律，数值计算了以下4种工况的流场和热流，分别是：

1） 来流参数不变，粗糙壁宽度不变，不同高度下的粗糙壁。

2） 来流参数不变，粗糙壁高度不变，不同宽度下的粗糙壁。

3） 来流参数不变，高度宽度均变化，固定宽高比的粗糙壁。

4） 粗糙壁高度和宽度不变，不同马赫数以及壁温下的粗糙壁。

根据以上4 种情况，在图3 展示了具体计算工况的高度和宽度分布，图3（a）列出了前3 种情况的粗糙壁高度和宽度分布，图3（b）列出了第4 种情况下的工况分布。共计算了28 个不同工况下的粗糙壁流场和热流，使用的网格流向与法向均已无关。同时，由于平板头部存在黏性干扰，主要分析0.2～1 m 的流场。在图3（c）与图3（d）中给出了高度0.421 2 mm、马赫数为6 时的计算结果的整体以及局部区域的速度云图。

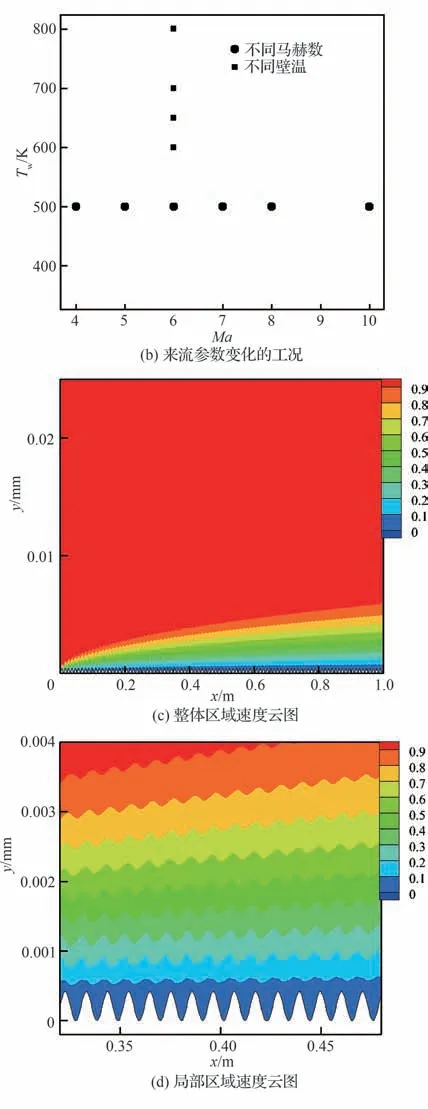
图3 计算工况以及典型计算结果Fig.3 Calculation conditions and typical calculation results

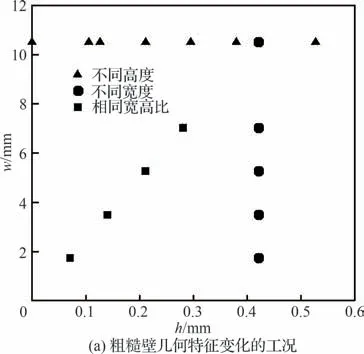
2. 1 不同高度下的壁面热流

首先分析第1 类工况下的壁面热流，即来流参数不变，粗糙壁宽度不变，计算不同高度下粗糙壁的基本流场。具体的粗糙元配置：宽度均为10.53 mm，高 度 分 别 为0、0.105 3、0.126 36、0.210 6、0.294 84、0.379 08、0.421 2、0.526 5 mm。

图4 给出了不同高度下，全场均布粗糙的壁面热流和光滑平板的对比，同时将壁面形状给出，方便与壁面热流做比对。从图4（a）可以发现，粗糙壁面的热流随壁面形式呈周期性变化，在正弦壁峰附近，热流达到峰值；同一流向位置的壁面峰值热流，随着高度的增加而增大，这一热增量不可忽略。由于粗糙元高度相比边界层厚度很小，因此热流的变化规律和壁面几何形状类似。图4（b）给出了局部放大的结果。图4（c）给出了较大高度（0.421 2 mm）下平均热流与光滑壁热流的比较，粗糙壁平均热流是对波纹粗糙元一个周期内的热流进行平均求得的，而光滑壁面的平均热流指相同流向区域的热流平均值。可见在微尺度的粗糙下，壁面平均热流增量是很小的，即使在较大高度下，微粗糙下的平均热流增量与光滑壁平均热流的比值小于3%，因此本文重点关注峰值热流。

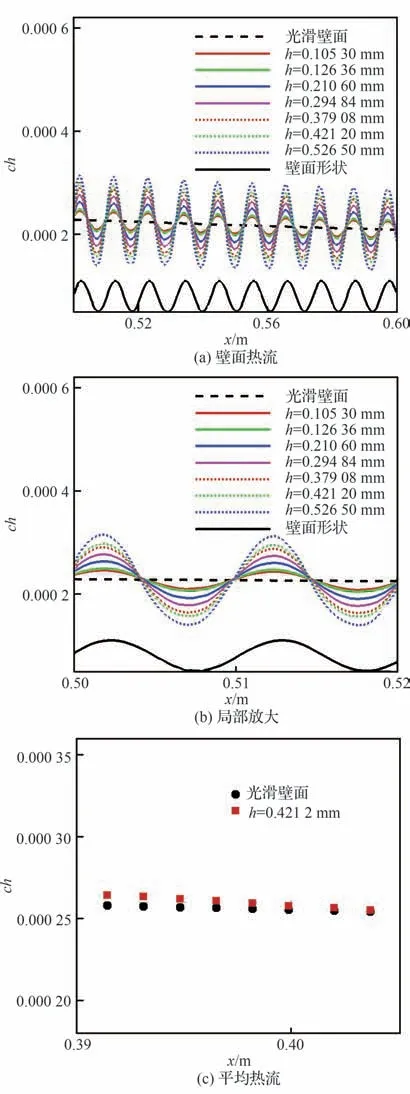
图4 不同高度下的壁面热流Fig.4 Surface heat flux at different heights

为了分析热流随着高度的变化规律，将不同流向位置的壁面峰值热流提取出来进行分析比较，对于每一个工况可以得到100 个峰值点，不同高度下的壁面峰值热流系数及相对热流增量Qratio如图5 所示。图5（a）给出了不同高度下的壁面峰值热流系数，可以发现随着流向位置x 的增大，壁面峰值热流减小；图5（b）则给出了不同高度下的相对峰值热流增量，很明显，沿流向的相对热流增量近似保持不变。同时，在同一流向位置，随着高度增加，壁面峰值热流和相对峰值热流增量均增大。壁面峰值热流沿流向位置的趋势与反比例函数的形式近似，随高度增大的趋势与线性函数近似，相对峰值热流增量与流向位置无关。为了确定壁面峰值热流与流向位置的具体关系，图6 给出了不同高度下壁面峰值热流与x-0.5的关系。从图中可以看出ch与x-0.5成线性相关关系，这一关系与光滑平板壁面热流和x-0.5的线性规律一致。

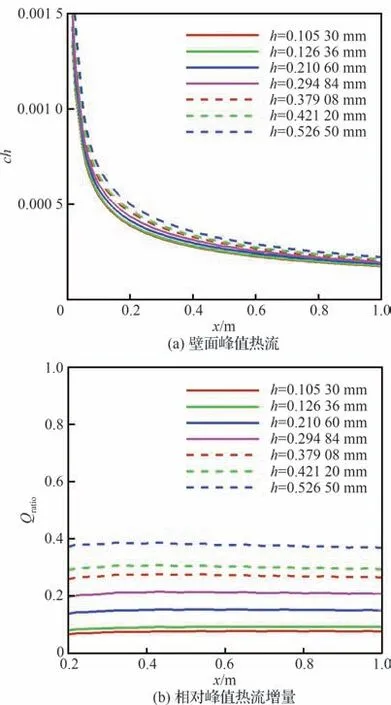
图5 不同高度下壁面峰值热流及相对峰值热流增量Fig.5 Surface peak heat flux and relative surface peak heat flux increment at different heights

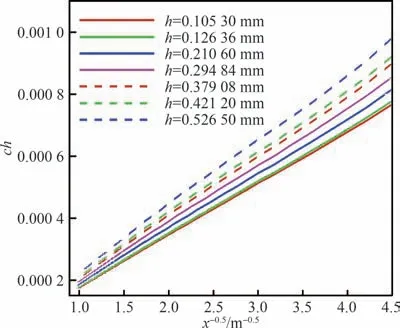
图6 不同高度下壁面峰值热流与x-0.5 的关系Fig.6 Relationship between surface peak heat flux and x-0.5 at different heights

图7给出了3 个不同流向位置下，壁面峰值热流随壁面高度变化的关系，很明显，ch与h 具有较强的线性相关性。因此，对于粗糙壁面峰值热流的计算，有理由做出以下假设：

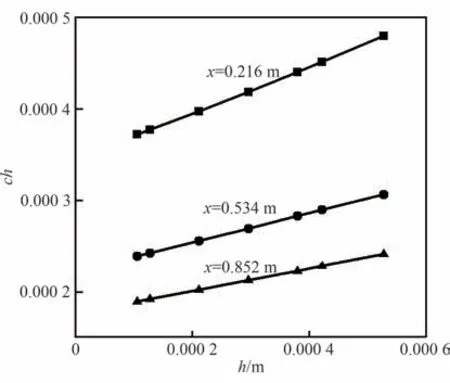
图7 不同流向位置壁面峰值热流与高度的关系Fig.7 Relationship between surface peak heat flux and height at different flow direction positions

式中：第1 项表示由于粗糙引起的热流增量，第2 项表示光滑平板的热流。由式（6）得到相对峰值热流增量为

式（8）与流向位置x 是无关的，符合图5（b）的规律。

2. 2 不同宽度下的壁面热流

对于第2 类工况，保持壁面高度不变，计算不同粗糙宽度的流场。使用的具体粗糙单元配置为：高度为0.421 2 mm，宽度分别为1.755、3.51、5.265、7.02、10.53 mm。对于小宽度，以0.4 m 为中心分布了100 个粗糙，在图中对应的曲线为这100 个粗糙的所在。

图8 显示了不同宽度下，粗糙壁面的热流结果与光滑壁面（x=0.4～0.41 m）的比较。可以看出，当粗糙带高度固定时，宽度越大，壁面峰值热流越小。

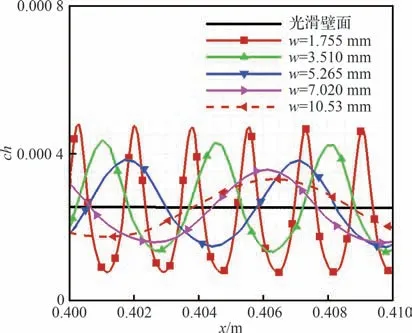
图8 不同宽度下的壁面热流Fig.8 Surface heat flux at different widths

图9 给出了粗糙壁峰值热流及相对峰值热流增量沿流向的演变规律。可以看到，随着粗糙宽度的增加，壁面峰值热流逐渐减小，但是整体并不成线性关系；同时，相对峰值热流增量也随宽度增加而减小。

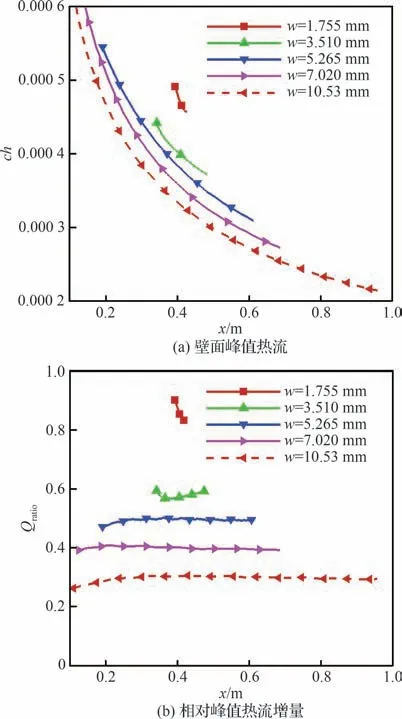
图9 不同宽度下的壁面峰值热流及相对峰值热流增量Fig.9 Surface peak heat flux and relative surface peak heat flux increment at different widths

2. 3 固定宽高比下的壁面热流

在得到上述关于热流与宽度成负相关的规律后，需要进一步确定壁面热流与宽度的定量关系。文献中常用Sigal-Danberg 参数来表征粗糙带特征，这一参数以高度与宽度的比值来定量刻画粗糙度特征。本节使用第3 类工况，目的是研究高度和宽度对粗糙壁面峰值热流的影响强度以及这两个因素之间比值规律，具体的粗糙壁参数见表2。

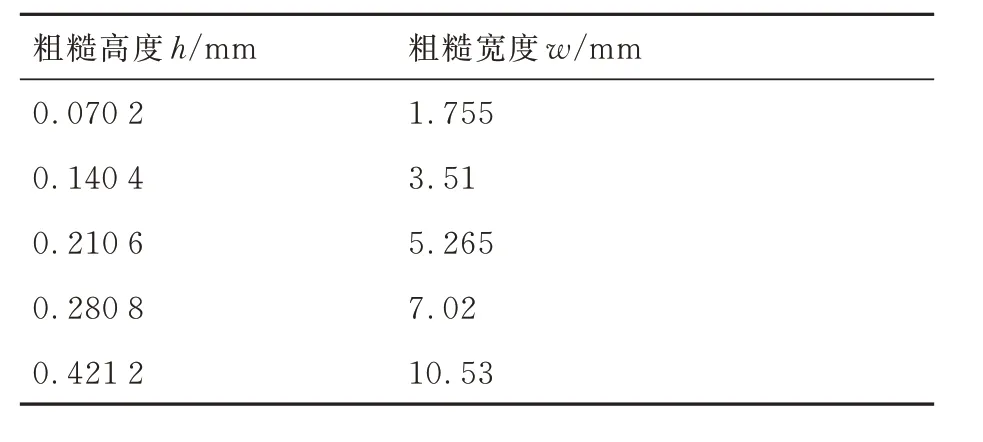
表2 固定宽高比的计算参数Table 2 Fixed aspect ratio calculation parameters

所取工况的粗糙宽高比均固定为25，假如宽度和高度对壁面热流有相同的影响强度，那么在固定宽高比的情况下，几种不同配置的粗糙壁面峰值热流在同一流向位置应是相同的。图10（a）给出了5 个工况下的壁面热流。可以看到，在固定宽高比的情况下，粗糙壁面峰值热流并不相同。图10（b）给出了每个工况的壁面峰值热流随流向x 的变化，可以发现高度越大，壁面峰值热流越大。这说明热流受高度的影响更大。同时，图10（c）进一步显示了相对峰值热流增量与流向位置的无关性。通过上述分析可以认识到，壁面峰值热流受高度的影响大于受宽度的影响，热流与宽度的幂次关系应该在-1～0 这一范围。

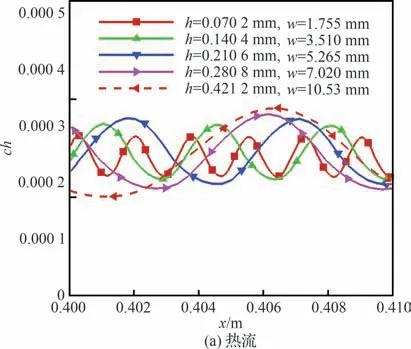
图10 相同宽高比下的壁面热流Fig.10 Surface heat flux with the same aspect ratio

2. 4 不同马赫数下的壁面热流

将粗糙壁面的宽度取为10.53 mm，高度取为0.379 08 mm，分析了不同马赫数（4、5、6、7、8、10）下的壁面峰值热流。图11（a）给出了粗糙壁面峰值热流结果的比较。可以发现，同一流向位置，在不同马赫数下，壁面峰值热流随马赫数的变化并非单调。这是由于光滑壁的热流本身随马赫数的变化就是非单调的。图11（b）给出了不同马赫数下，相对峰值热流增量的演变规律，可以发现同一流向位置，在不同马赫数下，相对峰值热流增量随马赫数增大而单调减小，但与流向位置x 无关，这一规律与前文相同。

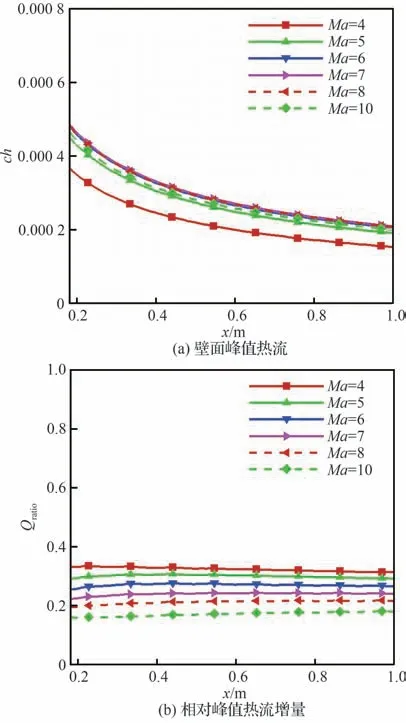
图11 不同马赫数下壁面峰值热流及其相对峰值热流增量Fig.11 Surface peak heat flux and relative surface peak heat flux increment at different Mach numbers

2. 5 不同壁温下的壁面热流

同样，研究壁温对于粗糙壁面热流的影响时，固定粗糙壁面的为宽度10.53 mm、高度0.379 08 mm，计算不同壁温（350、400、500、600、650、700、800 K）下的粗糙壁热流。

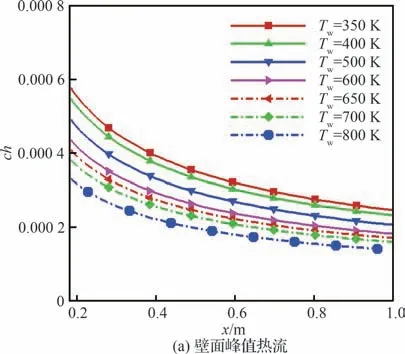
图12 显示了不同壁温下，全场均布粗糙的壁面峰值热流和相对峰值热流增量，可以发现，在同一流向位置，壁温越高，壁面峰值热流和相对峰值热流越小；相对峰值热流增量近似与流向位置无关。

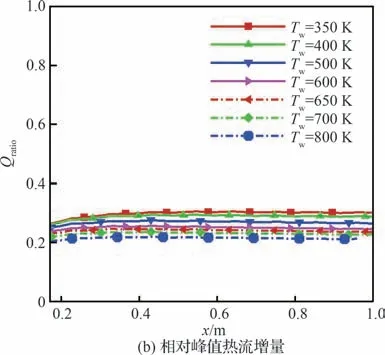
图12 不同壁温下的壁面峰值热流及相对峰值热流增量Fig.12 Surface peak heat flux and relative surface peak heat flux increment at different wall temperatures

3 热流预测模型

第2 节中不同高度、不同宽度、相同宽高比、不同马赫数以及不同壁温下，粗糙壁面峰值热流的定性变化规律可以概括为

1） 壁面峰值热流的变化与粗糙壁的高度成正比，与流向位置x 的0.5 次成反比；相对峰值热流增量与流向位置近似无关。

2） 壁面峰值热流的变化与粗糙壁的宽度成反比。

3） 壁面峰值热流受高度的影响大于受宽度的影响。

4） 相对峰值热流增量随马赫数增高而减小。

5） 相对峰值热流增量随壁温增高而减小。

在以上定性规律认知的基础上，为了进一步分析得到定量预测粗糙壁面峰值热流的模型，首先从光滑平板壁面热流的理论解出发给出热流预测公式的形式。

对于可压缩平板边界层相似性解，存在理论解用来计算热流，其具体推导过程见文献［28］。对于热流系数ch，理论解为

式（10）即光滑平板壁面热流的理论解。在之前的数值分析中，对粗糙壁面峰值热流做了的假设，当式（7）中的h=0 时，即表示光滑壁面的热流，应与式（10）相同，那么由此可得：

对于式（7）中第1 项粗糙壁引起的峰值热流增量，从第2 节的数值结果来看，显然，它的系数c1应与来流参数（马赫数、壁温比）和粗糙带的特征有关。结合第2 节中对粗糙带高度及宽度的数值分析结果，作出以下假设：

相应地，相对峰值热流增量为

式（13）中需要确定的参数有a、b 和C。使用2.2 节、2.4 节与2.5 节中得到的全场波纹壁上的峰值热流数值实验数据，计算其相对峰值热流增量（此量仅于马赫数、壁温比、粗糙壁特征有关，与流向位置无关）。对流向取平均，使用幂次关系拟合这个值与宽度、马赫数、壁温比的关系（分别对应2.2 节、2.4 节与2.5 节中的工况）。拟合的结果如图13 所示，图13（a）～图13（c）分别给出了对宽度、马赫数以及壁温的拟合结果。由拟合公式可以最终确定，C 为0.5，a 为2.67，b 为1.38。

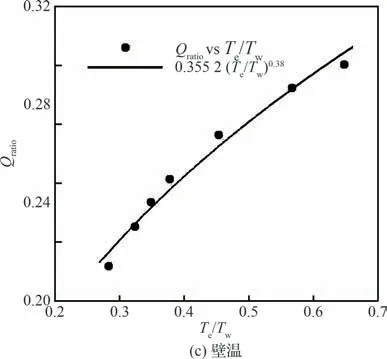
图13 热流预测公式幂次关系的修正Fig.13 Modification of exponential relationship of heating prediction formula

图14 给出了参数确定后，利用热流式（13）反求得到的不同宽度、马赫数、壁温情况下的Δ。可以发现这一常数整体集中在300～400 之间，根据本文的假设，即Δ 为表示粗糙类型的常数，通过将所有工况（均为正弦粗糙）先沿流向位置平均，计算得到的Δ 再取平均，最终确定正弦壁面的这一常数为322。

图14 热流预测公式中Δ的计算Fig.14 Calculation of Δ in heating prediction formula

这样可以得到预测粗糙带壁面峰值热流的公式：

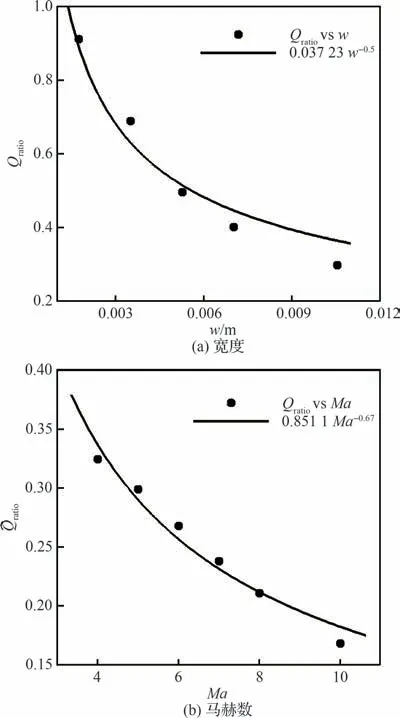
对于正弦波纹壁Δ可取322。那么，在已知粗糙壁的形状、位置、来流参数的前提下，可以使用式（15）预测由粗糙壁导致的壁面峰值热流。

4 预测模型验证

本文提出的壁面峰值热流预测公式需要进一步进行以下验证：一是基于相似性解得到的热流公式，与实际直接数值模拟得到的热流是否一致；二是式（15）在实际运用到粗糙壁的热流预测时，其误差及适用范围有多大。

4. 1 光滑壁面的热流验证

图15 给出了光滑壁面，在不同马赫数下基于相似性解通过变换得到的热流和热流预测公式（15）的比较，结果显示，两者得到的热流结果是一致的，这验证了理论推导过程的正确性。

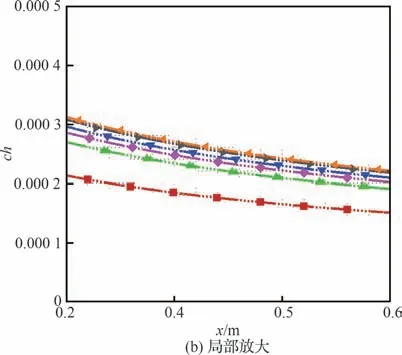
图15 相似性解热流结果与预测公式结果Fig.15 Similarity surface heat flux results and prediction formula results

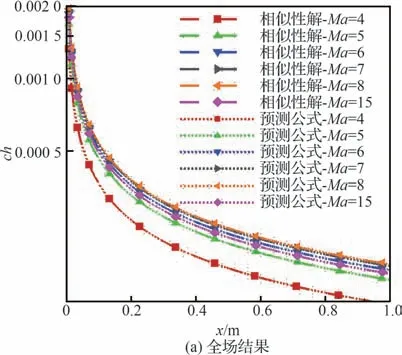
在光滑平板上，图16 给出了相似性解的热流结果与实际DNS 数值结果的比较，可以看出，两者的热流计算结果差距小于3%，吻合的较好，这验证了使用相似性解来计算热流的可行性。

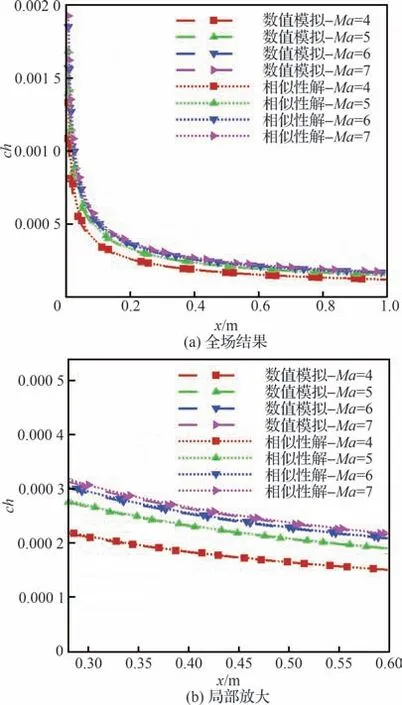
图16 相似性解热流结果与DNS 数值模拟结果Fig.16 Similarity solution surface heat flux results and DNS numerical simulation results

4. 2 全场均布波纹粗糙壁面的热流验证

完成对于式（15）理论依据的验证后，对其在预测粗糙壁面峰值热流时的误差进行分析。首先使用控制变量法，对高度、宽度、壁温、马赫数分别进行验证。使用相对误差以及绝对误差来衡量其大小。理论公式预测的壁面峰值热流与实际DNS 数值结果的相对误差：

式中：chDNS为直接数值模拟得到的热流系数。绝对误差：

式中：Qw 为有量纲的热流；Qwpredict为预测公式得到的有量纲的热流。

图17～图21 给出了在不同高度、不同宽度、相同宽高比、不同马赫数以及不同壁温下的壁面峰值热流的绝对误差和同一流向位置实际与预测结果的比较。同时将其相对误差在图中标出。可以看出，在大多数工况，除了在平板头部由于黏性干扰导致误差较大，下游的相对误差都在5%以下。值得注意的是，在不同宽度下的相对误差较大（＜10%），其原因可能为模型使用的用于衡量粗糙特征的幂次表达有一定的局限性，但绝对误差也可保持在一个较小的范围内。相同宽高比、不同马赫数以及不同壁温下的预测结果误差都在3%之内。表明在已有工况下，式（15）预测效果不错。

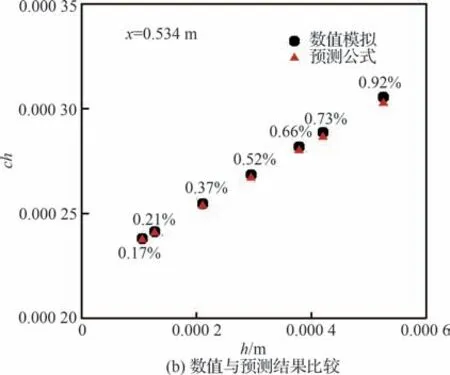
图17 不同高度下全场波纹壁预测公式与DNS 结果壁面峰值热流误差Fig.17 Surface peak heat flux error between full-field corrugated wall prediction formula and DNS results at different heights

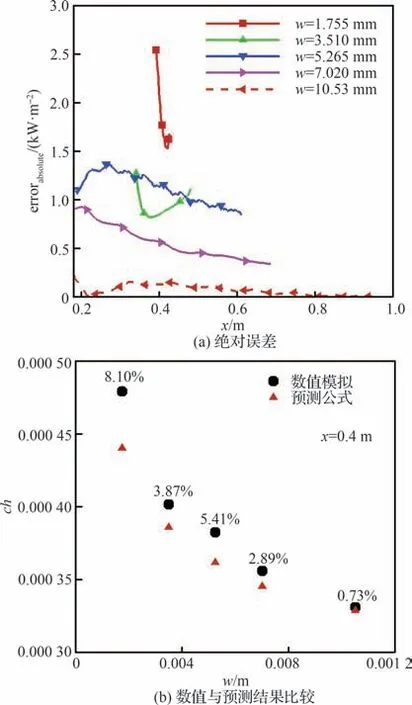
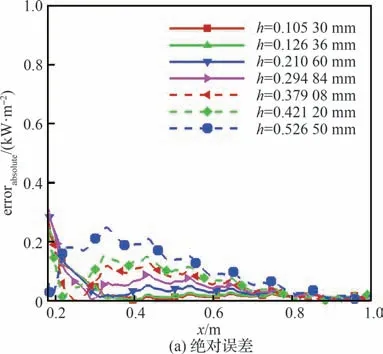
图18 不同宽度下全场波纹壁预测公式与DNS 结果壁面峰值热流误差Fig.18 Surface peak heat flux error between full-field corrugated wall prediction formula and DNS results at different widths

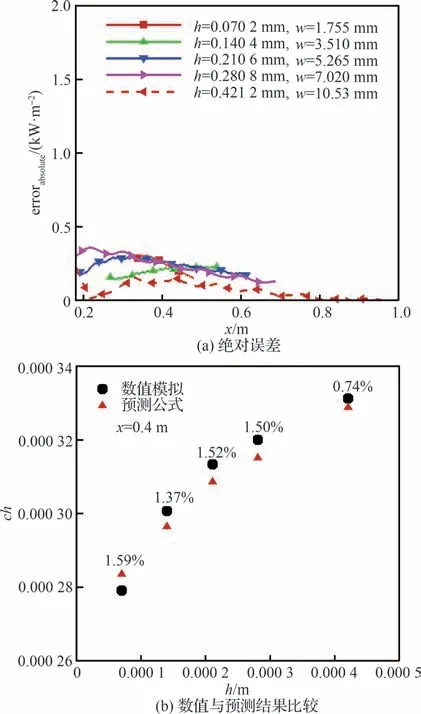
图19 相同宽高比下的全场波纹壁预测公式与DNS 结果壁面峰值热流误差Fig.19 Surface peak heat flux error between full-field corrugated wall prediction formula and DNS results with same aspect ratio

图20 不同马赫数下全场波纹壁预测公式与DNS 结果壁面峰值热流误差Fig.20 Surface peak heat flux error between full-field corrugated wall prediction formula and DNS results at different Mach numbers

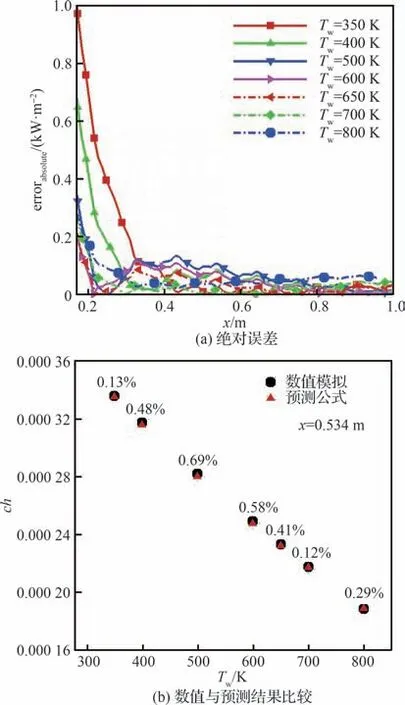
图21 不同壁温下全场波纹壁预测公式与DNS 结果壁面峰值热流误差Fig.21 Surface peak heat flux error between full-field corrugated wall prediction formula and DNS results at different wall temperatures

4. 3 测试工况的验证

为了进一步验证式（15）对于更为复杂的工况，即多变量均变化情况下的适用性，对更多的测试工况进行了验证。进行了高度、壁温、马赫数均变化的工况的验证，计算工况见表3。

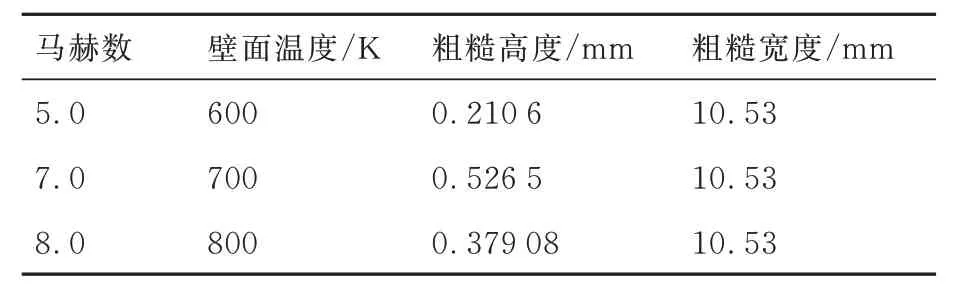
表3 测试工况的计算参数Table 3 Calculation parameters of test conditions

图22 给出3 个验证工况下的壁面峰值热流以及相对误差结果，可以看出，在多变量变化的情况下，所提出的预测模型的误差可以维持在较低的范围内（不超过3%），这也证明了式（15）对于多变量变化的复杂情况的适用性。

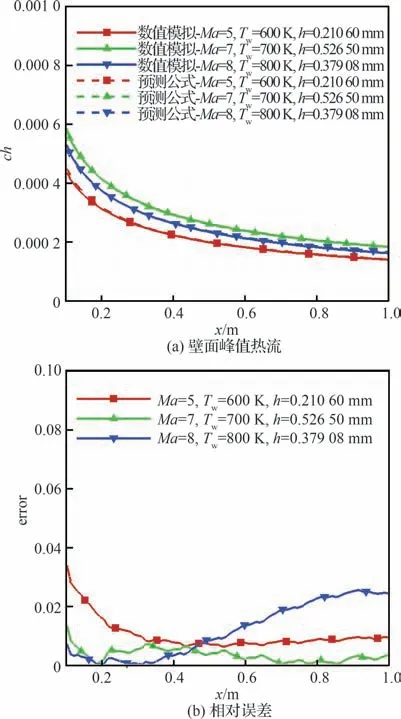
图22 测试工况验证结果Fig.22 Test case verification results

4. 4 极限工况的验证

对建立预测模型工况的壁温、马赫数的最大和最小值，即极限的几个工况，模型的适用性进行进一步验证的。使用的工况见表4。

表4 极限工况的计算参数Table 4 Calculation parameters of limited conditions

图23 给出壁面峰值热流比较以及模型预测的相对误差。可以发现，实际数值模拟的壁面峰值热流与预测公式的结果基本吻合；其中，马赫数为4、壁温为800 K 时的相对误差较大，原因在于此时壁温接近绝热壁温（841.51 K），热流较小，相对偏差会更大一些。

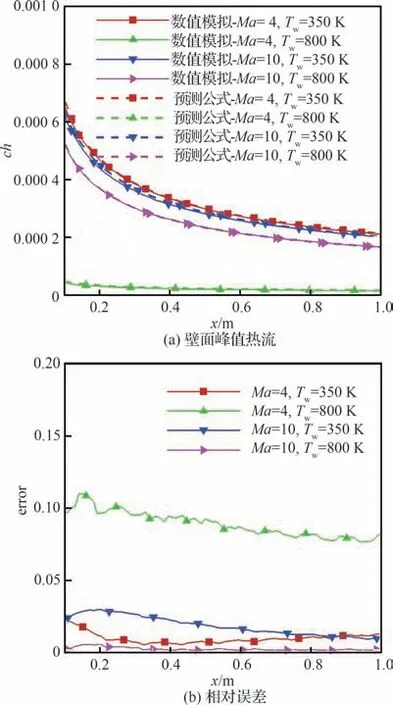
图23 极限工况验证结果Fig.23 Limited case verification results

4. 5 其他粗糙壁面形式的适用性

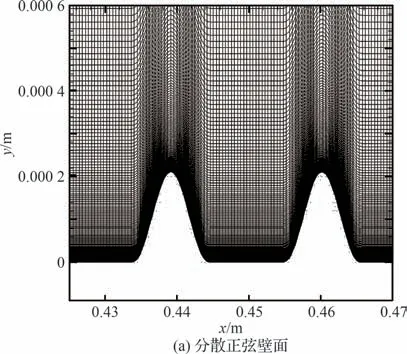
对于建立的热流预测模型式（15），详细验证了其对于正弦型连续波纹壁面的可用性，确定了其适用范围，为了进一步研究此模型对于其他壁面形式的适用性，数值计算分散的正弦型壁面以及椭圆型壁面，壁面形式如图24 所示。图24（a）为分散的正弦壁面，在0～1 m 的范围内，布置了50 个高度为0.210 6 mm、宽度为10.53 mm 的正弦型突起，相邻粗糙元之间的间距为10.53 mm，在粗糙元附近进行了局部加密；图24（b）为分散的椭圆壁面，在0～1 m 的范围内，布置了40 个高度为0.210 6 mm、宽度为7.02 mm 的椭圆型凸起，相邻粗糙元之间间距为14.04 mm，粗糙元附近进行了局部加密。两套网格流向分布2 501 个点，法向分布401 个点。

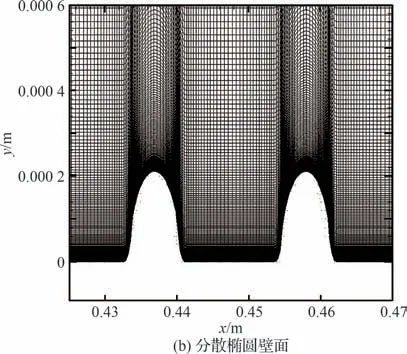
图24 壁面形状Fig.24 Wall shape

使用上述配置进行数值计算，在计算分散的正弦壁面时，Δ取322，与之前的正弦波纹壁是一致的，这是符合Δ表征粗糙带类型的常数这一假设的；而计算椭圆时，首先需要确定Δ，使用的方法与第4 节中方法相同，使用数值得到的相对热流增量求得Δ，发现其分布为1 条与流向无关的直线，符合对于Δ的定义，对所有流向位置得到的Δ取平均，得到Δ为300。图25 给出了不同壁面形式下粗糙附近的热流分布，不同壁面形式下，粗糙附近的热流变化是不同的。图26 给出了2 种形式下壁面峰值热流的变化规律，同时比对了其与预测值的差异，发现两者是基本吻合的。图27 则给出了壁面峰值热流预测模型的相对误差，可以看出，相对误差在2%以下，说明预测公式对于其他2 种壁面形状也具有一定的适用性。

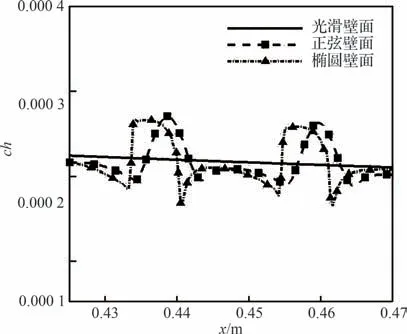
图25 不同壁面形式下的壁面热流Fig.25 Surface heat flux with different wall shapes

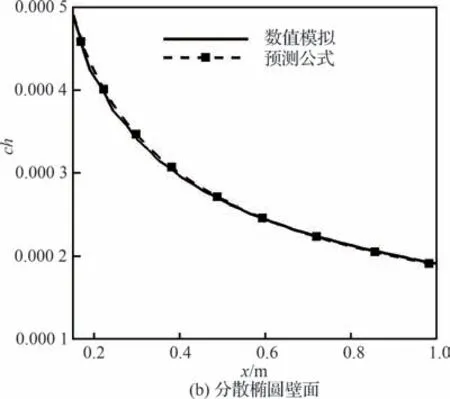
图26 不同壁面形式下的壁面峰值热流及其预测Fig.26 Surface peak heat flux and its prediction with different wall shapes

图27 不同壁面形式下的壁面峰值热流预测误差Fig.27 Prediction error of surface peak heat flux with different wall shapes

5 结 论

针对高超声速平板层流边界层，研究了表面均布高度小于600 μm 正弦型波纹凸起的粗糙导致的壁面热流的变化规律，并提出了一种可用于定量预测由波纹粗糙壁引起的壁面峰值热流的公式，详细验证了其适用性。

使用直接数值模拟研究粗糙壁在不同马赫数、高度、宽度以及壁温下的壁面峰值热流，发现壁面峰值热流的变化与粗糙壁的高度成正比，而与粗糙壁的宽度成反比；壁面峰值热流受高度的影响大于受宽度的影响；壁面相对峰值热流增量随马赫数增大而减小；壁面相对峰值热流增量随壁温增大而减小。

基于数值结果得到的定性规律，从光滑壁面热流的理论解出发，假设热流增量与粗糙高度、宽度、马赫数和壁温成幂次关系，得到预测粗糙壁面峰值热流的公式，并根据数据拟合得到了各幂次关系中的系数。首先通过控制变量法，对于宽度、高度、马赫数、壁温等单一变量进行了验证。然后验证了这些参数均变化时公式的有效性，并在极限工况下测试了其适用范围。最后在2 种不同的壁面粗糙形式下进一步探究了公式的可用性。整体上，预测模型的误差维持在8%以下。

本文关注的粗糙元都是缓变的，对于高度与宽度大小相当的粗糙元，本文的定性结论应该能够适用，但定量预测公式是否适用，还有待进一步研究。

致 谢

感谢中国空气动力研究与发展中心国义军研究员有启发性的帮助。