电力变压器的运行可靠性评估及剩余寿命预测研究

冯 凯

（中海石油（中国）有限公司湛江分公司，广东 湛江）

引言

变压器是电力系统中不可缺失的电气设备，供配电过程中，一旦变压器的运行发生故障，不仅会对系统整体运行造成影响，还会对营运方造成较大的经济损失[1]。因此，定期或有针对性的进行变压器维护，不仅可以提高其运行的可靠性，还可以提升变压设备的使用寿命。

在对变压器运行的进一步研究中发现，造成电力变压器运行故障的原因较多，包括变压器自身因素与外部环境影响，前者包括变压器出厂存在缺陷、经历短路次数过多等[2]。后者包括绕组绝缘事故、绝缘老化击穿、运行环境过于潮湿导致变压器外部导电、出口绕组变形、运行环境温度过高导致变压器处于高温运行状态等[3]。

变压器在运行过程中所产生的故障大部分为潜伏性故障，为提高变压器运行可靠性，实现对其运行状态与健康状态的评估，本文将开展如下所示的研究。

1 电力变压器的运行可靠性评估

1.1 提取电力变压器运行内部潜伏性故障影响因素

在不采取维修措施的情况下，随着电力变压器老化程度的加深，其运行可靠性呈现出逐渐下降的趋势[4]。图1 为变压器中绝缘纸抗张强度随运行年限增加的变化趋势。

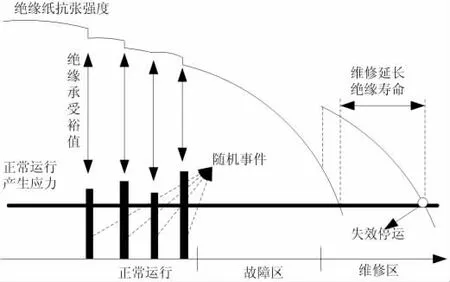
图1 变压器中绝缘纸抗张强度随运行年限增加的变化趋势

在绝缘老化程度加深的时候，它的运行可靠性会下降。而对变压器进行合理的维护，则能有效的提高其使用寿命，提高其工作的可靠性[5]。通常情况下，对变压器的维修策略包括：不完全维修、完全维修和最小维修。对维修策略的选择会影响到变压器故障率，具体而言体现在变压器状态转移速率上，其公式为：

电力变压器油中产气速率的计算公式为：

式中：γoil代表油中产气速率，C1代表第一次采样时的气体浓度，C2代表第一次采样时的气体浓度，Δt 代表第一次与第二次采样时的时间间隔，moil代表总油量，ρoil代表油的密度。在变压器运行过程中，油品气体生成率可以较好地反映其运行状态[6]。

1.2 电力变压器短期故障率计算

在明确电力变压器运行内部潜伏性故障影响因素后，通过下述操作可以实现对电力变压器短期故障率具体数值的求解[7]。假设变压器的状态概率矩阵为P（0），结合微分方程求解变压器状态转移矩阵为：

式中：P（t）代表变压器状态转移矩阵。对上述公式中的eAt进行多项式展开，将四阶及以上的多项式舍去得到新的多项展开式。当获得状态转移矩阵的特征后，即可求出矩阵的具体表达式，建立矩阵特征值求解等式为：

式中：s 代表状态转移矩阵的特征值。I 代表单位矩阵。在计算变压器的实际工作可靠度时，先采集了变压器的油品含气量的历史数据，再求出了各个状态间的平均传输率。另外，为了考虑到绝缘老化对变压器工作的影响，还需要对变压器绝缘线圈中的热斑、绝缘纸板中的水分进行实时监控[8]。

1.3 基于中长期故障率模型的变压器运行可靠性分析

在明确电力变压器短期故障率的计算方法后，构建中长期故障率模型，并基于该模型对变压器运行可靠性进行分析。获得N 组变压器处于任意时间点时的故障率。再结合监测得到的变压器油中气体含量和产气速率，确定变压器运行在某一状态时的故障率。图2为变压器中长期故障率预测模型。

图2 变压器中长期故障率预测模型

首先，根据变频器油层析的历史数据，对变压器从正常运行、报警、危险运行，直至发生故障所需的时间进行了分析。然后，利用MCMC 法，对变压器的故障循环进行情景仿真，得到了变压器在任何时间点的失效率。计算出了变压器的历史失效率，并将其与对应时间内的产气率、运行时间和运行状态进行了拟合。通过计算变压器失效率函数的系数，将油色谱实时监测数据引入到下述公式中，对变压器运行可靠性进行预测。

式中：λm（t）代表变压器故障率。ε、α 和β 代表待估参数。t 代表经历时间。λ0代表随机事件引起随机故障率。根据上述计算结果，得到变压器的故障率，计算1-λm（t）的结果，即为变压器运行可靠性预测的量化结果。

2 剩余寿命预测

2.1 建立电力变压器剩余时间概念模型

变压器的实际使用寿命很大程度上是由绝缘中的化学成分所决定的，在变压器的使用中，由于绝缘的老化或者是其本体结构受到了机械破坏，都会使绝缘寿命缩短。当变压器由目前的状态，进入到故障状态的时候，由于变压器绝缘损失比较严重，或者是油中的气体含量比较高，导致变压器不能正常工作而被迫停运，此时就需要技术人员进行相应的维修工作。因此，可以将电力变压器的故障状态作为其终点状态，明确电力变压器的剩余寿命主要是指变压器从当前状态到故障状态所需要的时间。建立电力变压器从当前无故障状态到故障状态的剩余时间概念模型，见图3。

图3 电力变压器从当前无故障状态到故障状态的剩余时间概念模型

图3 中，t1 代表变压在运行中处于健康状态（良好工况或运行状态）的监测时段。t2 代表变压在运行中处于告警状态的监测时段。t3 代表变压在运行中处于异常状态（故障状态或危险状态等）的监测时段。T1～T3 代表电力变压器从当前状态运行到故障状态所需要的平均时间。

2.2 剩余寿命预测

在此基础上，结合电力变压器在运行过程中的老化程度、作业环境、当前工况等，进行电力变压器故障率的定义，计算公式为：

式中：λ（t）代表在时间t 下的电力变压器故障率。f（t）代表寿命分布函数。F（t）代表时间t 下的电力变压器寿命密度函数。t 代表电力变压器运行时间。对上述计算公式进行规正与变形处理，得到下述公式：

对上述计算公式进行求解，得到F（t）。F（t）的求解计算公式为：

式中：C 代表常数项。μ 代表以μ 为计算变量的电力变压器运行故障率函数。计算过程中，考虑到F（0）=0，因此，求得常数项C 的取值为1。

由于电力变压器运行在t 时刻前未出现概率，因此，可以将其在运行过程中的可靠性描述为1-F（t），此时，可以根据如下公式，计算得到电力变压器在未来时刻下运行的可靠性函数表达式：

式中：R 代表可靠性函数。T 代表剩余平均寿命（电力变压器从当前无故障状态到故障状态所需要的时间）。t0代表监测时间点。根据上述研究内容，对变压器无故障运行的时间进行分析。计算公式为：

式中：M 代表无故障运行的时间。结合上述计算公式，进行电力变压器剩余寿命的预测，计算公式为：

式中：M'（t0）代表电力变压器剩余寿命的预测结果。在上述内容的基础上，对剩余寿命的预测求解过程进行描述，见图4。

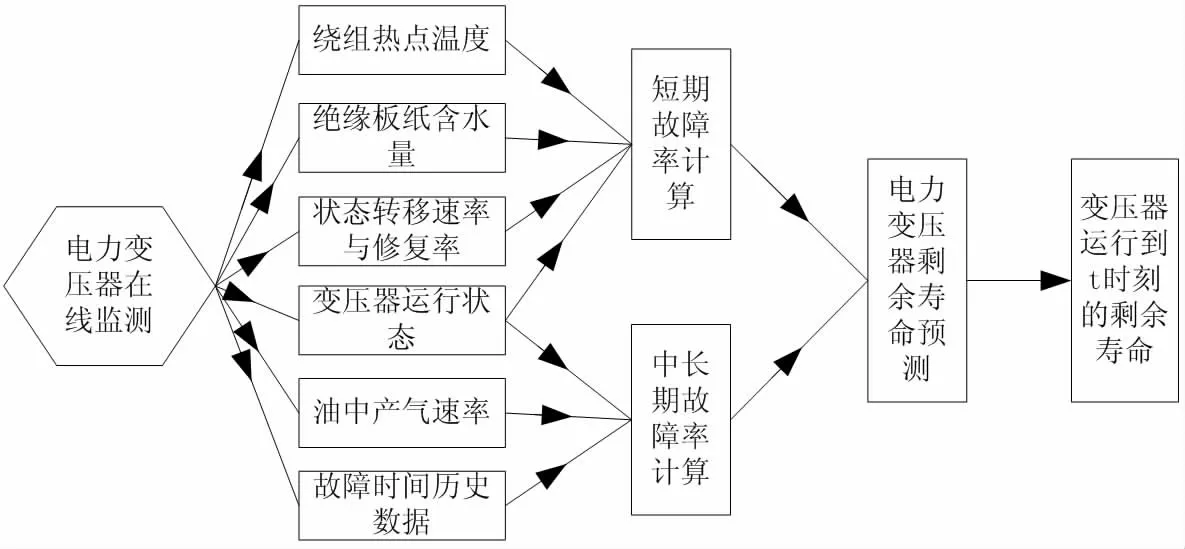
图4 电力变压器剩余寿命的预测求解过程

结束语

随着社会的快速发展，电力消费也在逐步增加。通过对变压器风险的科学评价，可以使变压器的缺陷得到及时地检测和修复，从而将损失降低到最小。在此基础上，考虑到变压器故障成因多样、影响因素复杂，因本次研究经验不足、认识程度有限、时间有限等原因，本论文尚有很多不足之处。因此，在后续的工作中，将根据电力变压器运行的实际情况，从变压器的绝缘老化角度入手，提取更多可能造成变压器隐性故障的因素，以此为依据，进行与之方面工作在实施中的进一步优化。此外，在后续工作中，还将加大对变压器设计、生产的监管，通过此种方式，降低由于自身原因引起的变压器运行故障，为变压器的规范化运行予以指示、帮助。