基于桩周土体位移的锚拉抗滑桩计算方法研究

李美霖

（贵州大学 土木工程学院，贵州 贵阳）

引言

锚拉桩是1980 年开始应用及发展起来的一种新型抗滑结构，由于其具有抗滑能力强、支挡效果好、施工方便、节省造价、设桩位置灵活、对滑体稳定性扰动小，施工安全等优点，在滑坡整治、高填、深挖或者深基坑治理中获得了广泛的应用。当前根据于两种方法计算抗滑桩：一种是基于土压力的方法，另一种是基于土体位移的方法[12]。目前，在国内锚拉桩的计算中，考虑桩- 土的作用大多数是沿袭普通抗滑桩的土压力法[12]，即假定滑坡推力为某种分布形式，戴自航[1]对土压力的分布进行了大量的研究。土压力法是先根据相应的假设经典塑性理论或者经典塑性理论来确定抗滑桩的桩侧极限土压力分布形式，因为被动桩侧土压力并不一定能够达到土压力极限值，所以这种方法并不能够对被动桩桩- 土相互作用的全过程进行分析[2]。同时虽然土压力法在一定程度上考虑到桩- 土的相互作用，但是不能考虑到锚索对土压力分布的影响，文献[3]运用FLAC3D 建立出三维数值模型，模型表明随着锚索预应力的增大，桩后滑坡推力的分布图形逐渐由梯形向矩形变化，而这种影响我们通常是没有考虑的。国外大多数将抗滑桩纳入承受侧向位移的侧向受荷桩范畴[4-9]，认为正是通过土体侧向位移才将荷载作用到桩上。根据于土体位移的方法能够直接依据土体位移计算桩身侧向位移、弯矩和桩侧土压力，能够对桩- 土相互作用的全过程进行分析[12]。H.G.Poulos[6]证明了基于土体位移方法的合理性；C.Y.Chen 等[7-8]基于位移加载的方法，进行研究单排抗滑桩的内力与变形；F.Cai 和K.Ugai[9]基于滑坡体位移，推导出单排抗滑桩内力与变形的解析解；目前仅限于对普通抗滑桩（被动桩）的研究，认为锚拉桩的位移法计算是非常有必要的，这是因为：第一，锚索初始张拉力，其产生的预加固力对滑坡推力有很大影响；第二，锚索的弹性支座作用也会对桩- 土相互作用有一定影响，从而影响滑坡推力；第三，由于锚索的存在，锚拉桩对于位移控制会更加敏感[12]。

基于此，本文在假定桩后土体位移随深度线性变化的前提下，分两个阶段建立出锚索抗滑桩的力学计算模型，并推导基于土体位移的锚拉桩力学解析解。应用Matlab 编程实现对锚拉抗滑桩的全过程力学分析[12]。

1 数值计算

将被动桩的力学模型延伸，并推广至锚索抗滑桩。应用Matlab 软件编写出基于本文提出的数学解析表达式的计算程序，此计算程序可以用来计算不同深度处桩身的响应及弯矩和最大位移。由于为了验证模型的正确性，从而建立如图1 所示FLAC3D 有限差分数值模型，类似该形式的有限差分数值模型已经得到了证明，因此可以很好的进行对桩- 土相互作用探究[9，11]。

图1 FLAC3D 数值模型

模型分为滑体、基岩、桩三部分，滑体厚10 m，基岩厚15 m，模型长度为25 m。桩间距4 m，锚固深度6 m，抗滑桩截面尺寸为1.5 m×2 m，模型材料性质如表1 所示。对称性建模，模型底部约束z 方向的位移，前后边界约束y 方向的位移，左侧基岩边界约束x方向的位移，右侧边界约束x 方向的位移，左侧滑体边界在初始平衡阶段约束x 方向的位移。在加载阶段对滑体左侧边界施加1×10-5m/步的位移。

表1 三维数值模型材料参数

（1）普通抗滑桩分析

值得说明的是，令前文GDj=0，R0j=0，则本文解析结果退化为普通悬臂桩的计算结果，为证明本文解析结论的普适性，首先对不加锚索全埋桩模型滑体左侧边界施加12 mm 的平动位移。图2 和图3 为桩底固定位移法解析计算结果、数值模拟结果、传统压力法（桩前、后分布力均考虑为矩形）对比图。本文解析结果桩顶位移6.8 mm，对抗滑桩的挠度拟合较好，虽然桩身最大弯矩与数值结果有43%的差距，但是弯矩趋势一致，源于数值模拟参数的复杂性，认为本文模型能较好模拟桩土相互作用。与此同时压力法由于不能考虑桩土相互作用，无论位移还是弯矩都与实际值显示出了较大的差距，究其原因传统压力法滑坡推力作用点通常取的比较高，而桩前抗力作用点取的比较低。

图2 悬臂桩挠度图

图3 悬臂桩弯矩图

（2）锚索抗滑桩分析

将上述模型桩前土体挖去（设为空NULL），在抗滑桩距桩顶1 m 处加设一束水平预应力锚索（Cable单元），如图5 所示。锚索自由端长度25 m，一端固定，另一端锚固于桩体内，截面面积为As=12×139×10-6mm2，锚索弹性模量Es=1.8×108kPa，初始应力为500 KN, 模型其他参数不变。滑体左侧边界施加12 mm 的平动位移。图4 和图5 为桩底固定位移法解析计算结果、数值模拟结果、传统压力法（桩后分布力考虑为矩形）对比图。从图中可以看出本文解析结果对数值模拟结果拟合程度较好。传统土压力法锚索计算锚索拉力为753 KN，而解析计算结果锚索拉力为628 KN，这是因为本文解析方法考虑到了预应力张拉阶段产生的预加固力作用。

图4 锚索桩挠度图

图5 锚索桩弯矩图

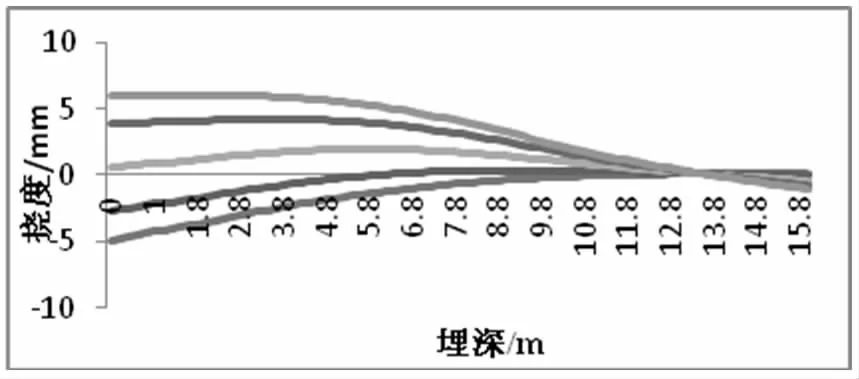
图6 不同滑坡体位移锚索抗滑桩挠度

图7 不同滑坡体位移锚索抗滑桩弯矩

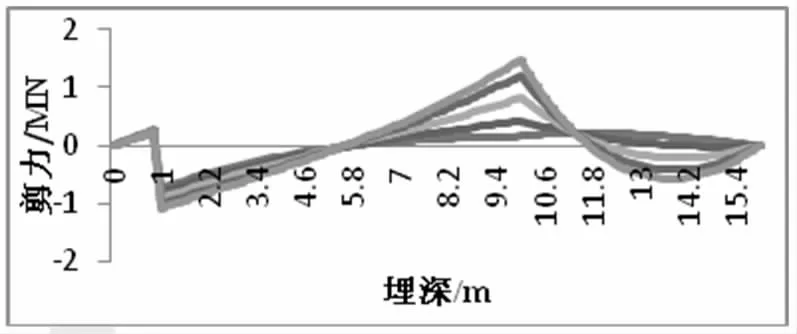
图8 不同滑坡体位移锚索抗滑桩剪力

（3）滑坡体的桩- 土相互作用全程分析

对前述锚索抗滑桩分别施加0 mm，2 mm，5 mm，8 mm，10 mm 的桩后滑体平动位移。图6-8 反映了锚拉桩内力和位移的动态调整过程。分析表明桩身内力和位移的动态变化过程呈现了较强的规律性，在桩参数和地质参数确定的情况下，随着桩后岩土体的推移，桩身内力和位移图绕某一确定点做旋转运动。该点的位置与桩的刚度对桩周岩土体的相对刚度有关。

从图9 可以看出随着桩后土体位移的增大，桩后岩土体推力呈现了由倒三角- 倒梯形- 矩形- 梯形的变化过程。说明初始张拉预应力是影响桩后滑坡推力分布的一个非常重要的因素，照搬普通抗滑桩固定不变的推力分布形式对锚索桩进行设计，显然是不合理的。

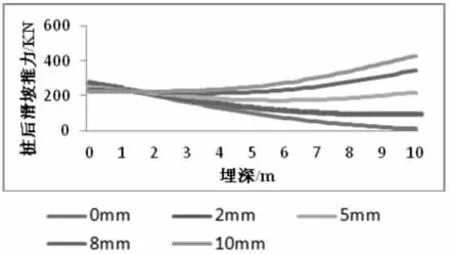
图9 不同滑坡体位移滑坡推力分布

同时桩后岩土体的桩后侧移模式（平移、梯形、倒三角）也会对桩身内力和位移产生重要影响，限于篇幅，本文暂不做分析，读者都可以应用本文所建立力学模型进行很好的分析。

2 结论

（1）本文分两个阶段建立了根据桩周土体位移的锚拉抗滑桩弹性地基梁模型控制方程组，力学概念非常明确，考虑锚索初始张拉锚索支座作用和锚索初始张拉对桩- 土相互作用的影响，应用初参数法给出了桩身力学响应的数学解析解。

（2）编制了Matlab 计算程序进行桩身响应的计算，并与FLAC3D 数值模拟结果、传统压力法计算结果进行了比较，表明本文计算模型可较好的模拟桩-土- 锚索的相互作用，传统压力法由于对于滑坡推力和桩前抗力作用点的位置通常与实际差别较大，导致传统压力法计算相对较保守。

（3）对于锚索抗滑桩桩- 土相互作用全过程分析，得出一些有规律的认识，表明该模型具有很好的实用价值，对锚拉抗滑桩的设计计算研究有较强的指导作用。同时不仅可以应用于普通工况，对于一些较复杂的外部因素作用下，比如超载、开挖、降雨或地震等因素，边坡土体局部或瞬态大变形乃至失稳滑动，使抗滑桩产生附加位移及弯矩等复杂工况具有更好的应用空间。