基于 ARMA 模型的变压器噪声逆向还原实验研究
2023-07-28田昊洋徐鹏贺林吴欣烨叶强生
田昊洋 徐鹏 贺林 吴欣烨 叶强生
摘 要:基于声辐射理论和激光测振原理,通过实验测量干式变压器模型的表面振速和辐射噪声声压,分别采用表面振速法和频响函数法求得变压器的声辐射指数。在此基础上,采用自回归滑动平均(ARMA)模型开展变压器噪声逆向还原研究,获取声压与声压级预测值,并与实验值进行对比。结果表明:采用频响函数法得到的声辐射指数比采用表面振速法得到的约大1.0~1.5 dB;采用基于 ARMA 模型的噪声预测算法得到的声压与实验得到的声压约相差0.015 Pa,声压级约相差1 dB;利用基于 ARMA 模型的预测算法和激光测振原理进行噪声逆向还原具有较好的可行性,且可推广应用于其他结构辐射噪声的预测。
关键词:变压器;声辐射指数;噪声;表面振速法;频响函数法
中图分类号: TM421 文献标志码: A
Experimental study on the reverse reconstruction of the transformer noise based on ARMA model
TIAN Haoyang ,XU Peng ,HE Lin ,WU Xinye ,YE Qiangsheng
(1. State Grid Shanghai Electrical Power Research Institute, Shanghai 200437, China;2. State Grid Shanghai Municipal ElectricPower Company, Shanghai 200122, China;3. School of Energy and Power Engineering, University of Shanghai for Scienceand Technology, Shanghai 200093, China)
Abstract:In terms of the acoustic radiation theory and laser vibration measurement theory, both the surface vibration velocity and sound pressure of radiation noise from a dry-type model transformer were measured. And the frequency response function method and surface vibration velocity method were used to obtain the sound radiation index of the transformer, respectively. The autoregressive moving average model (ARMA) was used for the reverse reconstruction of transformer noise. And the predicted values of sound pressure and its level were obtained and compared with the experimental data. Results show that the sound radiation index obtained by the frequency response function method is 1.0~1.5 dB larger than the calculated results by the surface vibration velocitymethod. The difference of sound pressure and its level between the ARMA model and the test is 0.015 Pa and 1 dB, respectively. The ARMA model and laser vibration measurement method for the noise reverse reconstruction has good feasibility and can be used for the prediction of radiation noise of the other structures.
Keywords:transformer; sound radiation index; noise; surface vibration velocity; frequency response function
变电站是保障电网系统有效运行的关键设备之一,其发挥着变换电压、接受和分配电能、控制电流及调整电压等重要作用[1–2]。近年来,随着居民区配电变压器增多,户外变压器和居民楼之间的距离减小,变压器辐射噪声污染问题愈发突出,对居民健康和生活环境产生了严重影响[3],加之人们环保意识逐渐加强,关于变压器噪声的投诉时常发生[4]。变压器噪声产生机理、监测及控制是目前该工程领域面临的重要挑战之一,有效识别变压器噪声,并在其复杂结构中进行声源定位是缓解变电站噪声问题的关键技术之一。
针对变压器噪声的产生与控制,国内外学者开展了较为广泛的研究。 Ming 等[5]利用声强法对大型电力变压器设备的远近场辐射特性進行了研究,指出变压器振动和辐射噪声均由一系列主要在前几个谐波频率(100 Hz)处的分量组成,并且变压器辐射特性不会受到变压器上、下盖噪声辐射的影响。Zawieska[6]通过建立相似模型来模拟变压器油箱,并在箱体上布置扬声器来研究变压器噪声特性和有源控制,开发出可主动降低大功率电力变压器噪声的系统。董志刚[7]较为全面地阐述了变压器噪声的产生机理与声学特性,指出变压器空载噪声主要受铁芯振动的影响。谭闻等[8]和王常平等[9]均指出振动是产生变压器本体噪声和冷却系统噪声的主要原因,且噪声源控制在工艺设计以及安装注意事项等各方面都应受到高度重视,以便有效降低噪声。
声压法和声强法是测量噪声的主要手段。Girgis 等[10]利用声压法和声强法对室内和室外变压器的噪声进行了测量,发现声强法的测量结果比声压法的更准确,但是当背景噪声越大,声波反射越强时,两者的测量结果都不准确。其主要原因是变压器噪声由本体噪声和冷却系统噪声组成,在空气中以声波的形式向四周扩散[11],具体表现为:①实际变电设备噪声的产生机理与传播路径复杂,其运行环境除包括各种固定的背景噪声(如冷却风扇与电抗器振动引起的噪声)外,还包括其他突发的非固定噪声(如碰撞、说话、风雨及雷电等)。②变压器是一个由多部件相互耦合的振动系统,包括变压器铁芯、绕组、油箱等结构,当各部件振动的固有频率趋近于硅钢片磁致伸缩振动的基频率及其整数倍时,由于谐振现象变压器噪声显著增加[12]。上述诸多因素给变压器噪声识别和逆向还原带来了巨大挑战。因此,开展变压器噪声识别和逆向还原,准确识别和定位噪声来源是目前该领域研究的重点和难点之一。
本文基于声辐射理论和激光测振原理,开展变压器箱体噪声识别研究,得到变压器箱体各表面声辐射指数,采用基于自回归滑动平均(ARMA)模型的噪声预测算法对声压和声压级进行预测,并将预测值与实验值进行对比,以验证噪声逆向还原技术的可行性。
1 理论依据
1.1 表面振速法
计算结构表面辐射噪声时,引入辐射比σ以判断结构的辐射效率[13]。辐射比与振动结构本身的固有特性有关,也与激励力以及结构周围的边界条件有关,其定义为结构声辐射射入半空间(即结构的另一侧)的声功率除以与该结构具有相同表面积和相同振动速度有效值的结构所辐射的声功率,即
式中:ρ为声阻抗;Sv 为结构辐射面积;?(v)为平均振速; W 为结构辐射声功率;c 为流体介质中声波速度。
在工程实践中,常采用声功率级、振速级等评价指标,因此将辐射比的表达式改写为
式中:ρ0c0=400 Ns ·m?1,为空气特性阻抗,ρ0为基准声压, c0为流体介质中声波初始声速;S0为基准面积;?(v)0为平均基准振速; W0为基准声功率。
将式(2)转化为声辐射指数与声功率级、振速级的关系式,可得
式中,10lgσ为振动物体向远场辐射能量的声辐射指数。
通过测量声压级得到声功率级,即
式中: Lw 为声功率级; Sp 为声压测量表面面积; Lp 为声压级。
通过实验采集振速信号和声压信号,并计算振速级与声压级,将声压级转换成声功率级,从而获取变压器噪声的声辐射指数。
1.2 频响函数法
在单位时间内通过结构辐射面积 Sv 的声功率和声压的关系为
式中:I 为发光强度;ω为角频率;P 为基频率。
由式(5)可得到声辐射指数与噪声声压、表面振速的关系为
引入表示为结构表面振速与辐射噪声的关系的频响函数 H=P(ω)/v(ω),则式(6)转变为
因此,通过实验测量结构表面频响函数并计算辐射比,可得变压器噪声的声辐射指数[14]。
1.3 激光测振原理
采用激光测振方法测量变压器表面振动具有精度高、响应速度快以及不受现场环境影响等优点。激光测振原理示意图如图1所示。激光测振是利用激光干涉效应测量表面振动。激光束经过分光镜后被分解为测量光束(穿透分光镜的光束)和参考光束(被分光镜反射的光束)。其中测量光束由振动物体反射后,再经过分光镜反射,到达光电探测器表面;参考光束由平面反射镜反射至分光镜,穿透分光层并在光电探测器表面与测量光束汇合而形成干涉现象[15]。
设测量光束与参考光束的角频率、振幅均分别为ω0、A0,相位角分别为θ1、θ2,空间位移差为δ, 波长为λ, 物体振动位移为 x ,则测量光束的复振幅α1和参考光束的复振幅α2分别为
合成光束的复振幅α为
式中:t 为时间;θ、A 分别为合成光束的相位角和振幅。
由于光强与振幅的平方成正比,则合成光束的发光强度为
式中,β为比例系数。
当物体振动λ/2时,光强完成一个强弱变化的周期。通过记录光强强弱周期变化总数 n ,可求得物体振动位移 x=nλ/2。通过测量多普勒频率f0,可求得物体振速 v=λf0/2。
1.4 ARMA 模型
ARMA 模型由自回归(AR)模型和滑动平均(MA)模型组成。ARMA 模型计算式为
式中:yt 为时间序列;φi 为自相关系数;θj 为滑动平均系数; at 为随机项;μ为常数项; i 为自回归阶数;j 为滑动平均阶数;p 为 AR 部分的阶数; q 为 MA 部分的阶数。
将 ARMA 模型经差分变化转变为差分整合移动平均自回归(ARIMA)模型。ARIMA 模型将一个非平稳的时间序列变为平稳的时间序列,从而保证了数据的稳定性。该模型是对 ARMA 模型的补充,其计算式为
式中: B 为延迟算子; d E Z ,d>0。
2 实验与分析
2.1 实验方案
实验中变压器箱体的尺寸参考额定容量为30 kVA 的 SCB10干式变压器设定。为准确测试变压器辐射噪声,避免外界环境噪聲的影响,实验在半消声室中进行。图2为测试现场。采用振动加速度传感器测量变压器箱体表面振速。为使实验结果具有普遍性,在同一工况下重复采集每个测点的振动信号3次,并确保每次测量时传感器的位置相同。
变压器振动测点图如图3所示,其中正、反面,左、右侧面分别布置16个测点。采用激光振动测试仪对变压器模型中每个测点的频响函数进行测量,其中每隔10 cm 布置1个测点,测点距离变压器表面30 cm。待信号波形平稳后开始测试,测试时长为5 s。变压器高度 h=62.5 cm,分别在 h/3、h/2和2h/3三个高度进行测量,其中每个高度设有35个测点。
2.2 结果分析
图4为测点 A 振速、声压时域图。0~5 s 时振速、声压变化范围分别为?0.0050~0.0085 m · s?1、?0.8~0.7 Pa。可见,振速、声压信号均为平稳周期信号,此时变压器为稳态声源。
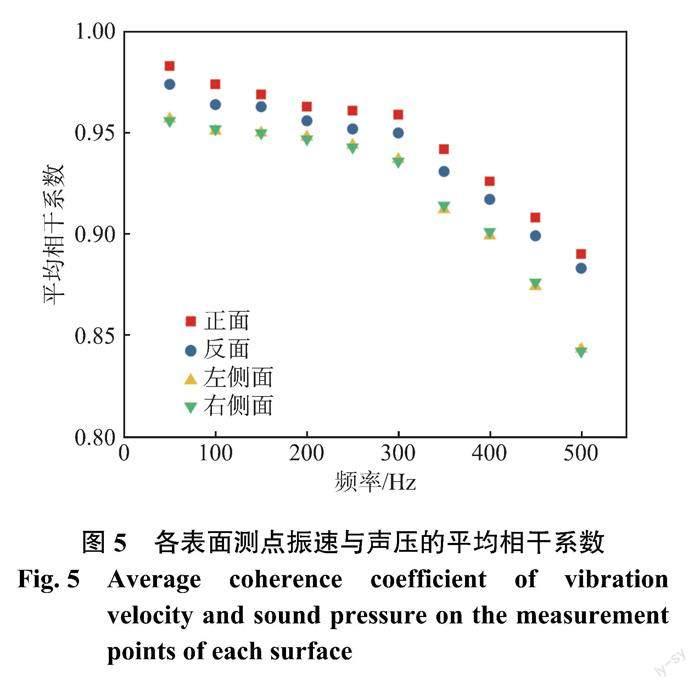
通过计算得到在50~500 Hz 频段的平均振速功率谱和平均声压功率譜,从而获得各表面测点振速与声压的平均相干系数(剔除小于0.8的值),结果如图5所示。由图可知,在50、100、200和300 Hz 时振速和声压具有较好的相干性,两者的相关系数大于0.9。在400~500 Hz 频段上,相干系数随着频率增加显著减小。可见,在50、100、200和300 Hz 时,变压器振动和噪声具有很好的相干性,表明实验测试数据可靠。
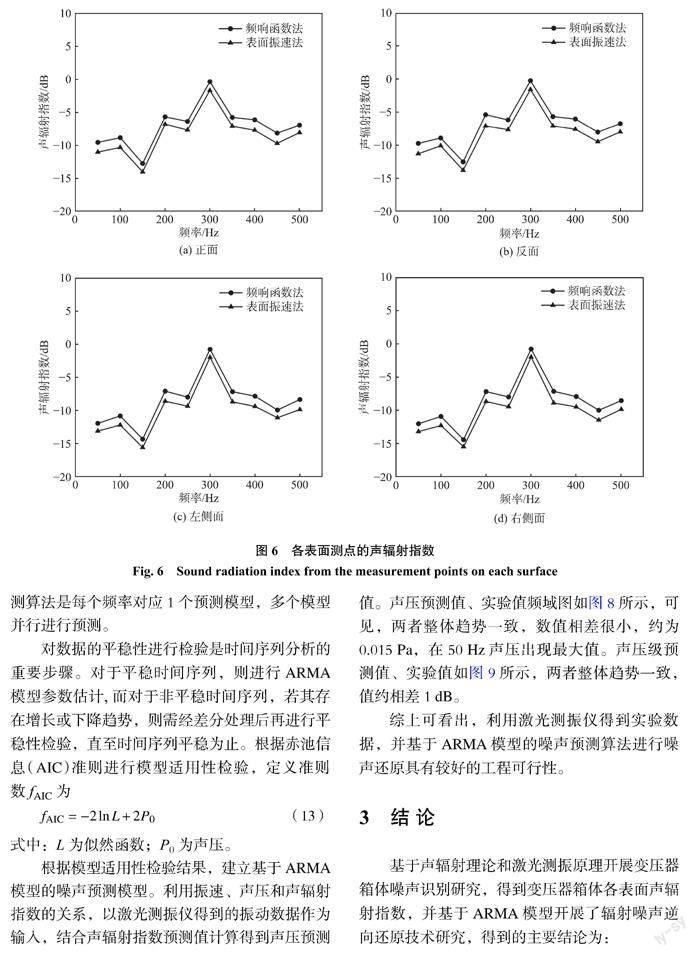
分别采用频响函数法和表面振速法计算变压器各表面测点的声辐射指数,结果如图6所示。可见,分别采用频响函数法和表面振速法得到的声辐射指数变化趋势相同,数值上也较接近。其中变压器正、反面,左、右侧面的声辐射指数在300 Hz 时出现最大值,其值接近于0,表明变压器各表面的300 Hz 振动分量几乎完全辐射为噪声,这符合平板噪声辐射理论;声辐射指数在150 Hz 时出现最小值,可见150 Hz 振动分量对噪声贡献较小,且左、右侧面的声辐射指数最小值均比正、反面的小。采用频响函数法得到的声辐射指数略大于采用表面振速法得到的结果,两者约相差1.0~1.5 dB,可满足工程测量要求。因此,基于激光测振原理,再由频响函数法计算得到声辐射指数的方法具备一定的可行性。该方法可为噪声几何预测模型中相关参数的精确设置提供参考。
2.3 噪声还原
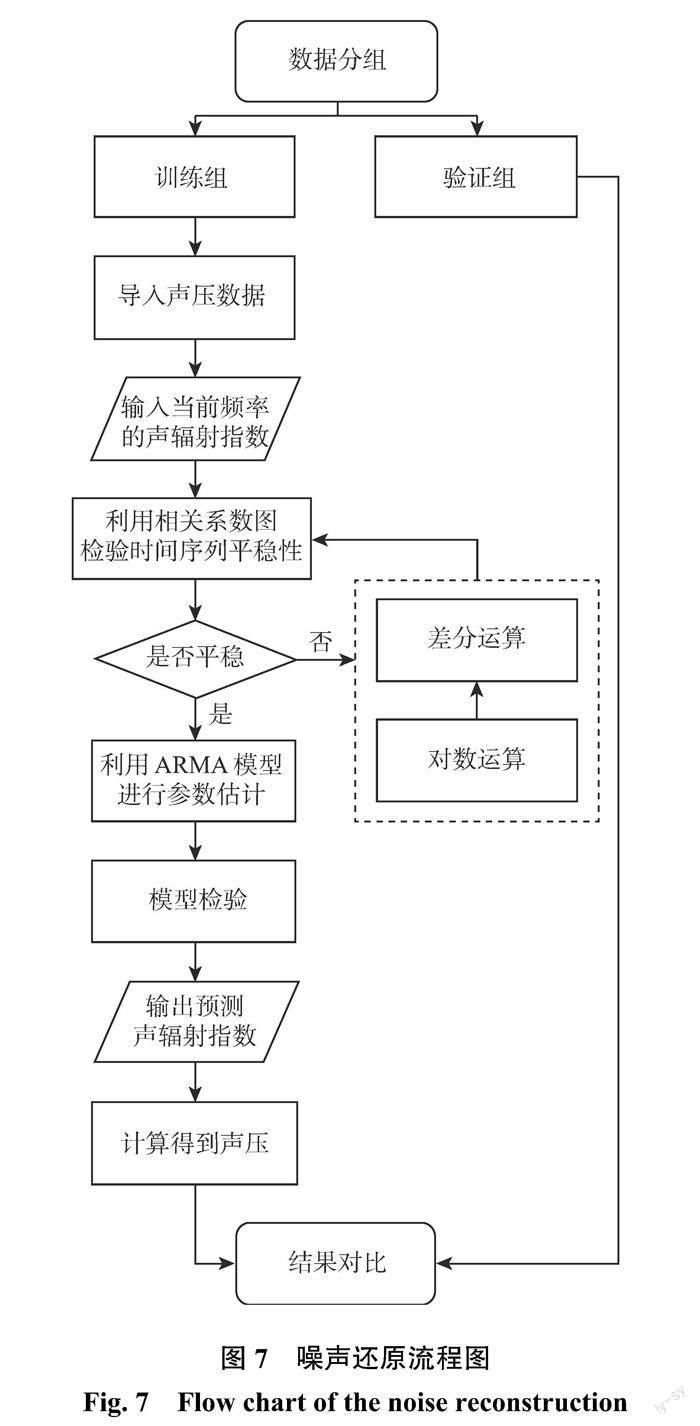
噪声还原流程如图7所示。将测试时长为3 min 的数据均分为36组(5 s 为1组),其中前24组为训练组,后12组为验证组。将训练组作为预测模型的输入,对各频率下声辐射指数进行 ARMA 模型预测。基于 ARMA 模型的噪声预测算法是每个频率对应1个预测模型,多个模型并行进行预测。
对数据的平稳性进行检验是时间序列分析的重要步骤。对于平稳时间序列,则进行 ARMA 模型参数估计, 而对于非平稳时间序列,若其存在增长或下降趋势,则需经差分处理后再进行平稳性检验,直至时间序列平稳为止。根据赤池信息(AIC)准则进行模型适用性检验,定义准则数fAIC 为
式中: L 为似然函数; P0为声压。
根据模型适用性检验结果,建立基于 ARMA 模型的噪声预测模型。利用振速、声压和声辐射指数的关系,以激光测振仪得到的振动数据作为输入,结合声辐射指数预测值计算得到声压预测值。声压预测值、实验值频域图如图8所示,可见,两者整体趋势一致,数值相差很小,约为0.015 Pa ,在50 Hz 声压出现最大值。声压级预测值、实验值如图9所示,两者整体趋势一致,值约相差1 dB。
综上可看出,利用激光测振仪得到实验数据,并基于 ARMA 模型的噪声预测算法进行噪声还原具有较好的工程可行性。
3 结论
基于声辐射理论和激光测振原理开展变压器箱体噪声识别研究,得到变压器箱体各表面声辐射指数,并基于 ARMA 模型开展了辐射噪声逆向还原技术研究,得到的主要结论为:
(1)通过对比频响函数法和表面振速法两种计算方法发现,采用两种方法得到的结果变化趋势一致,且数值吻合较好。采用频响函数法得到的声辐射指数比采用表面振速法得到的计算结果略大1~1.5 dB,说明通过频响函数法获得变压器声辐射指数具有较好的可靠性。
(2)基于激光测振原理,将采用基于 ARMA 模型的噪声预测算法得到的预测值与实验值进行对比,结果表明,声压、声压级预测值和实验值整体趋势一致,两者声压约相差0.015 Pa,声压级约相差1 dB。可见,基于 ARMA 模型的噪声预测算法具有较好的可行性,该方法可应用于各类结构的辐射噪声预测。
参考文献:
[1]孙宜林, 祝敏, 王宏骏.变电站电力设备运行监测与维护[J].百科论坛电子杂志, 2018(14):364.
[2]刘海峰, 赵永生, 谭建群, 等.智能变电站技术应用现状和展望[J].湖南电力, 2013, 33(S1):9-14.
[3]杨朝阳.住宅小区公用配电站降噪措施研究[D].北京:华北电力大学(北京), 2017.
[4]周喆.住宅小区变压器噪声分析及降噪措施探讨[J].科技风, 2018(7):191,193.
[5] MING R S, PAN J, NORTON M P, et al. The sound- field characterisation of a power transformer[J]. Applied Acoustics, 1999, 56(4):257-272.
[6] ZAWIESKA W M. Power transformer as a source of noise[J]. International Journal of Occupational Safety and Ergonomics, 2007, 13(4):381-389.
[7]董志刚.变压器的噪声(2)[J].变压器, 1995(11):27-31.
[8]谭闻, 张小武.电力变压器噪声研究与控制[J].华东电力, 2012, 4(4):687-688.
[9]王常平, 林云志, 王国伟, 等.如何降低变压器噪声[J].变压器, 2004, 41(6):29-30.
[10] GIRGIS R S, GARNER K, BERNESJO M, et al. Measuring no-load and load noise of power transformers using the sound pressure and soundIntensity methods-Part-I: outdoors measurements[C]// Proceedings of the 2008 IEEE Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century. Pittsburgh: IEEE, 2008:1?8.
[11]李诚理.配电房干式变压器噪声分析及减振降噪处理[J].机电信息, 2020(2):70-71.
[12]江世云.降低电力变压器噪声的设计探讨[J].大众用电, 2020, 35(6):33-34.
[13]田昊洋, 胡敏, 彭伟, 等.表面振速法在干式变压器噪 声测量中的应用[J].噪声与振动控制 , 2016, 36(5):196-200.
[14]胡静竹, 王延召, 周兵, 等.油浸式变压器声辐射效率分析[J].变压器, 2020, 57(10):76-82.
[15]于梅, 杨丽峰, 刘爱东, 等.激光测振仪在振动标准装置校准中的应用研究[J].计量技术, 2009(2):52-55.
