凸显“量” 弱化“率”——《分一分（一）》教学设计及思考

文|杨 梅 徐文琦

【教学内容】

北师大版三年级下册第67～69 页。

【课前思考】

一、叩问学生起点在哪儿

从知识结构上看，学生已经认识整数，现实生活中有平均分的经验基础，听说也见过分数的形态，只是对分数意义的理解不清晰。从认知规律上看，整数到分数是数概念的一次扩展，学生能利用“一半”的生活经验感悟分数产生的必要性，但较难理解分数既能表示一个具体的量，也能表示整体与部分的关系。由此发现，学生不是零起点，教师要依据学情明确分数的初步认识需要教什么，要重点教什么。

二、追问知识联系在哪儿

对于分数意义的学习，教材分为两个阶段，三年级教学分数的初步认识和五年级教学分数的意义。细观单元内容，知识点涵盖比大小、运算、问题解决、分数与除法的关系等等，分析整个知识结构的关联性与一致性，发现“分数单位”是核心概念之一。分数和整数一样，都是用计数单位来表达的，它贯穿在分数意义、比大小、运算教学中。分数单位不仅有助于理解分数是“数”，像整数计数一样可以数出来，也能帮助学生明晰分数运算的算理。对此前联后延的核心概念，教师要整体把握设计，学生才能学得透彻，学得明白。

三、反问整体建构在哪儿

基于对知识结构及认知结构的分析，需要摒弃以零碎单一的知识点为载体的传统课时教学，它在一定程度上割裂了知识之间的联系。要站得高，看得远，在厘清知识与认知结构的基础上，关注方法与思维结构以增加学习的效度和深度。因此，我们在“认识分数”大单元教学中发现，从三年级第二课时开始，教材基本呈现的都是表示“率”，从而影响学生对于分数是“数”能表示“量”的理解，因此要延续整数认识的大观念来认识分数的意义，感悟“量”，体会分数单位作为核心目标，突出分数的本质特征，从整体视角理解分数的意义，感悟分数与整数概念的一致性。

【教学过程】

一、以图导入，唤醒数的价值

1.从数概念引出课题。

导入：过去，我们已经认识了很多数来表示物体的数量，你能快速说出这些小正方体有几块吗？（从1000 块-100 块-10 块-1块，平均分成10 份，1 块平均分成2 份，每一份是多少？怎么表示？）

师：是的，不到1 块、一半、二分之一块，整数不能表示，可以用分数表示，就是一个分数，今天，我们一起来认识分数。

2.学习分数的各部分名称。

认识分数线、分子、分母，会写、会读。

【设计意图：借助直观说数，体会整数表达的是对完整个数的抽象；分数表达的是非完整数量的抽象，但它们都可以用来表示具体的数量。同时依托分一分，让学生利用“一半”的生活经验感悟分数产生的必要性，知道在数系的扩充中，分数是整数的延续，是数概念的一次扩展。】

二、数形相依，建构分数模型

2.小组合作探究，初步认识分数。

师：这些分数都表示谁的数量？一起来看看。（课件依次出示）

●活动一：请用以上分数表示出下图中的涂色部分或圈出来的部分，小组合作完成。

活动要求：（1）观察：图形或物体有什么共同点？

（2）思考：分数与对应的图，它们有什么联系？

（3）表达：分数表示什么意思？

3.反馈交流。

（1）观察发现：共同点都是平均分。

（2）思考发现：分母指的就是图形（物体）平均分的份数，分子指的就是取的份数。

4.抽象分数概念。

生：因为不管是什么东西，只要把它平均分成3 份，取其中的1份，就能用表示它的数量。

小结：看来，把一个物体或图形平均分成几份大小，取其中的一份大小就是几分之一，取几份大小就是几份之几。

5.感悟分数单位的累加过程。

师：（聚焦第5 幅图，动画添加涂色部分）你有什么发现？

师：真不错，用数一数的方法发现了整数和分数之间的联系。

【设计意图：提供丰富的现实材料让学生从数形结合的表象“由表及里”地观察、比较、分析，引导学生用发现问题、分析问题、解决问题的逻辑性找到分母、分子与平均分的份数、表示的份数之间的联系，深入理解分数的本质。同时教学过程中，持续呈现分数表示数量的多少，加强学生对于分数表示“量”的认识，并渗透分数也是分数单位的累加。】

三、多元表征，凸显分数本质

●活动二：创造一个分数。

1.出示活动要求，独立完成。

（1）思考。你想创造一个什么分数？表示谁的数量？

（2）操作。利用不同形状的纸折一折、涂一涂，也可以在纸上画一画。

（3）表达。在小组里说一说你创造的分数意义。

2.分层次呈现学生资源。

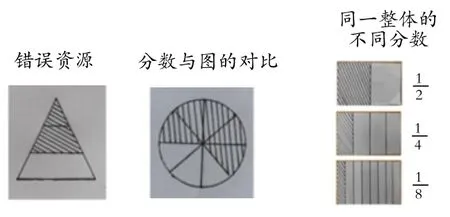
（1）交流你创造的分数表示的意义。

【设计意图：让学生经历丰富自主的“创造分数”活动，将学生生成的素材充分挖掘，通过分析、讨论等高频率、多维度、深层面的交流巩固分数意义，加深对分数是分数单位累加的认识，提高学生的分析、类比迁移能力和自主探索能力。】

四、借助模型，化具体为抽象

生：我发现它们都不到1 米。

2.在数轴中体现。

师：现在我把它们都移到了这条数轴上，利用刚才的发现，你还能联想推理到什么？或是你有什么问题？

生：我想问为什么到数轴上没有单位了？与刚才的有什么不同？

生：这些分数都在0 至1 之间，1 至2 之间还有没有分数？

师：真会思考，就让我们带着这些问题在后续继续学习分数，你们的猜想与问题都会得到验证与解决。

【设计意图：从在1 米上表示不同长度到数轴中“1”的几分之几，让学生从直观表达“量”到抽象体会“率”，帮助学生初步感受到分数既可以表示物体数量的多少（量的意义），也可以表示部分是整体、一个量是另一个量的几分之几（率的意义）。同时让学生展开推理，提出问题，初步进行分数单位大小的比较，也为后续学习假分数、带分数奠定基础。】

五、课堂总结（略）