综合运动求交与约束求并的机构自由度分析方法

卢文娟, 李兴艳, 孙迪贺, 曾嘉豪, 樊大宝, 曾达幸

(1.东莞理工学院 机械工程学院,广东 东莞 523808, E-mail: zengdx@dgut.edu.cn; 2.燕山大学 机械工程学院,河北 秦皇岛 066004)

自由度是机构最基本的性质之一,是综合新机构的先决条件,是运动学和动力学分析的基础,是确定驱动配置的前提[1-2]。自由度的研究已有一百多年的历史,学者们从机构组成、运动方程、雅可比矩阵零空间以及李群、李代数等多个角度提出了几十种具有代表性的自由度公式[3]。随着多环耦合机构[4]、折纸机构[5]、变胞机构[6]等新型复杂机构的不断涌现,上述自由度计算公式不再具有普适性与准确性[7]。究其原因,传统自由度分析方法没有考虑并联机构中同一构件存在两个或以上作用效果相同时产生的过约束问题,从而导致机构的理论自由度和实际运动特征并不相符[8]。因此,如何解决机构中出现的过约束问题便成为自由度分析方法的重中之重。

为了避开机构存在的过约束问题,采用对机构的分支运动和动平台的运动求交集的方式对机构末端执行器的自由度进行计算求解[9]。Gogu等[10]基于线性变换原理建立了自由度公式,其在对机构连通度进行求解的过程中采用了运动求交的思想;Rico等[11-12]基于李群、李代数建立了自由度公式,其关键参数的求解内含了运动求交的思想,随后又利用实例对其进一步分析[13];杨廷力等[14]基于方位特征集建立了自由度公式,其方位特征方程的运算规则主要基于运动求交思路建立;高峰等[15-17]基于GF集理论建立了运动求交运算规则,并将其引入机构综合研究中。

上述运动求交思想的自由度分析方法无需建立机构的运动方程或运动螺旋,简化了机构自由度求解过程,但其在机构末端运动耦合、分支不明确以及分支数目多等应用场景下仍存在一定局限性[18]。基于此,运用机构约束力和约束元素求并集的自由度分析方法进行补充。黄真等[19]引入反螺旋理论以分析机构自由度,并从约束的角度提出修正的G-K公式;于靖军等[20]在对约束线等效简化的基础上,运用约束求并的思想建立了自由度分析的图谱法;Li等[21]在几何代数的框架下,基于约束求并思路提出了一种少自由度并联机构自由度分析方法,并利用几何代数外积性质判别和剔除冗余约束。显然,约束求并思想在内部约束复杂的机构自由度分析中具有一定优势,且其对运动求交思想的局限性进行了有效扩展[22]。

综上,基于运动求交与约束求并思想的自由度分析方法各有优势,结合两种自由度分析思路在各自应用场景中的特点,本文建立了两种自由度分析方法的统一表达形式,并提出了一种综合运动求交和约束求并的机构自由度分析方法,主要包括:借助数学符号描述机构的运动特征和约束特征,明确分支和动平台相关参数的表示形式,阐述自由度分析求解的基本步骤;基于图谱法的线图元素清晰、直接的表达机构运动和约束的关系,从避开过约束的角度提出基于运动求交的机构自由度分析方法;面向多自由度分支组成的并联机构,将过约束视作一般约束,提出基于约束求并的机构自由度分析方法;建立综合运动求交与约束求并的机构自由度分析方法,并通过两种典型的机构算例验证了其应用于复杂机构自由度分析的高效性和实用性。

1 自由度分析参数定义

1.1 基本概念

(1) 定义构件L相对构件M的构件参数表示为

位置参数中α-Sa、β-Sb、γ-Sc可替换为α-li、β-lj、γ-lm,表示α、β、γ转动轴线经过直线li、lj、lm;或者替换为α⊂AB、β⊂CD、γ⊂EF,表示α、β、γ转动轴线属于平面AB、CD、EF。“⊂”符号表示属于,“AB”符号表示包含AB的平面。规定若转动轴线位置是任意的,则在位置参数中不进行表示。

根据上述构件参数的定义,给出以下其他参数定义:

① 分支参数:并联机构动平台、第k条分支、 定平台构成开式运动链,其中动平台相对定平台的构件参数称为分支参数,记作Gk,表示分支k输出的运动空间;

② 动平台参数:对于并联机构,动平台相对定 平台的构件参数称为动平台参数,记作GB,表示动平台的运动空间。

(2) 定义构件L相对构件M的构件约束参数表示为

位置参数中x-Sa、y-Sb、z-Sc可替换为x-li、y-lj、z-lm,表示约束力x、y、z经过直线li、lj、lm;或者替换为x⊂AB、y⊂CD、z⊂EF,表示约束力x、y、z在平面AB、CD、EF上。规定若约束力的位置是任意的,则在位置参数中不进行表示。

根据上述构件约束参数的定义,给出以下分支约束参数和动平台约束参数的定义:

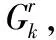
1.2 参数求解

(1) 分支参数的求解

分支参数包括方向参数和位置参数,其中方向参数可由分支螺旋系的二次反螺旋表示的运动方向确定;位置参数可通过二次反螺旋表示的转动轴线位置得到。

(2) 分支约束参数的求解

分支约束参数也包括方向参数和位置参数,其中方向参数由分支螺旋系的反螺旋表示的约束力和约束力偶方向确定;位置参数通过反螺旋表示的约束力位置得到。

2 运动求交方法

利用运动求交方法展开自由度分析过程,借助交空间中向量表示法[23]以及图谱法中的线图元素以数形结合的方式建立角速度求交规则和线速度求交规则,同时清晰的阐述自由度分析过程。

2.1 基本求交规则

在全局坐标系下对所有分支参数求交,若分支参数中的第i个位置的速度元素为“0”,那么求交结果的第i个位置元素为“0”,若分支参数中存与第i个位置元素耦合的元素,则求交结果在耦合元素位置的元素也为“0”。

例如:

式中:G1的第2、3、5、6个位置的元素为“0”,G2的第3、4、5、6个位置的元素为“0”,则求交结果第2、3、4、5、6个位置的元素为“0”。G2的α1、β1元素的上角标相同,表示相互耦合,因此求交结果第1个位置的元素为“0”。

2.2 角速度元素求交规则

在图谱法理论中,表示机构自由度和约束的图谱元素集合称为线图。

图谱元素如表1所示,约束线用点划线表示,其中点划线、两端带箭头点划线的物理意义分别为约束力、约束力偶,约束线图由约束线张成;自由度线用直线表示,其中直线、两端带箭头直线的物理意义分别为转动自由度、移动自由度,自由度线图由自由度线张成。直线和带箭头的直线分别对应螺旋理论的线矢量、偶量。

表1 图谱元素表示

在图谱法理论中,一对相交的转动自由度线可确定径向线圆盘,如图1所示。空间内汇交的三条转动自由度线可确定径向线球,如图2所示。

基于上述图谱法理论,角速度元素求交的过程可概括为首先在机构简图上对角速度元素对应的转动自由度线进行标记,得到每个分支转动自由度线在空间中的分布情况,然后可知各分支内相交转动自由度线确定的径向线圆盘、径向线球,最后根据如表2所示的角速度元素求交规则确定所有分支转动自由度线的交集空间,交集空间的基对应的角速度元素即为求交结果。

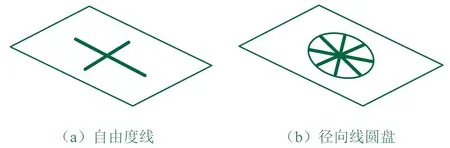
▲图1 一对相交转动图谱分析

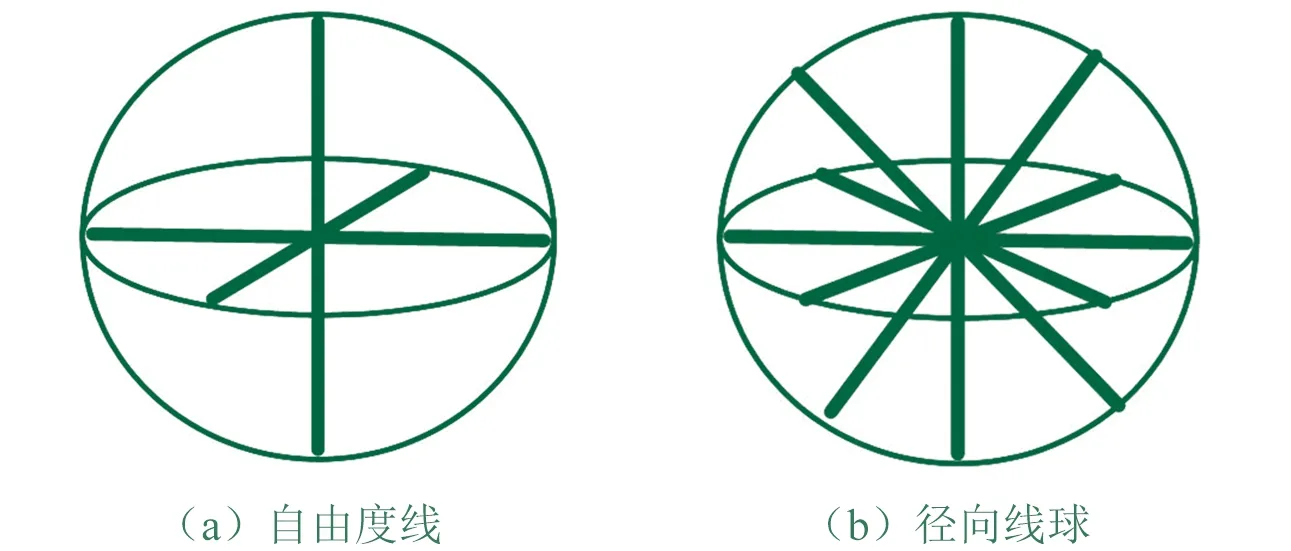
▲图2 空间内汇交图谱分析

表2 角速度元素求交规则

2.3 线速度元素求交规则

为了对线速度元素求交,首先介绍交空间中向量表示法:已知V1=L(a1,a2,…,ar)、V2=L(b1,b2,…,bs)是数域F上的n维子空间,a1,a2,…,ar是V1的基,b1,b2,…,bs是V2的基,存在x1,x2,…,xr,y1,y2m…,ys∈F,建立齐次线性方程组为

x1a1+x2a2+…+xrar-y1b2-…-ysbs=0

(2)

该齐次线性方程组系数矩阵为[a1a2…ar-b1-b2…-bs]。若方程组仅存在零解,则V1∩V2为空,若V1∩V2存在非零解,齐次方程组的基础解系为

(3)

齐次方程组的解χ1、χ2、…χn为

(4)

借助上述交空间中向量表示法,建立线速度元素求交规则。不妨假设在全局坐标系下,并联机构分支参数Gk中方向参数表示的线性无关的线速度为vk1、vk2、…、vkn(n≤3),则分支k输出的移动空间为Vk=L(vk1,vk2,…,vkn)。

于是建立线速度元素求交规则:若已知所有分支输出的移动空间V1、V2、…、Vk交集的基,则基中的列向量表示的线速度元素为分支参数中的线速度元素的求交结果。

移动空间V1、V2、…、Vk交集的基可由交空间中向量表示法两两求交获得,具体过程如下:

所有分支输出移动空间的交集为

V1∩V2∩…Vk={…[(V1∩V2)∩V3]…}∩Vk

(5)

根据交空间中向量表示法求出V1∩V2的基ε1,以基ε1建立移动空间Vε1,此时式(5)变为

V1∩V2∩…Vk={…[(Vε1∩V3)∩V4]…}∩Vk

(6)

然后同理可得Vε1∩V3的基ε2,以基ε2建立运动空间Vε2,那么

V1∩V2∩…Vk={…[(Vε2∩V4)∩V5]…}∩Vk

(7)

以此类推可知:

V1∩V2∩…Vk=Vεk-2∩Vk

(8)

根据交空间中向量表示法求得Vεk-2∩Vk的基εk-1,εk-1为V1、V2、…、Vk交集的基。

基于图谱法中转动轴线位置的推论确定完整的分支参数,根据分支参数的求交规则可确定动平台参数,得到机构末端件自由度的符号解,即得到机构末端件自由度分析的运动求交方法。

3 约束求并方法

利用约束求并方法展开自由度分析过程,以分支约束参数为出发点建立相应的求并规则,使用相同的数学符号和几何元素阐述求解过程,明确运动和约束之间的关系,间接确定动平台的方向和位置。

3.1 分支约束参数

分支约束参数求并规则包括约束力偶元素、约束力元素求并规则两部分。

(1) 约束力偶元素求并规则

在全局坐标系下,以分支约束参数中约束力偶元素为基构建约束力偶空间。各个分支的约束力偶空间的并集为动平台的约束力偶空间。动平台的约束力偶空间的基是所有分支约束力偶空间的基组成的矩阵的极大无关组,对应的约束力偶元素可作为各分支约束参数中约束力偶元素的求并结果。

则求解过程可以描述为在全局坐标系下,将所有分支约束参数中约束力偶元素表示的约束力偶作为列向量组成矩阵,通过线性列变换求矩阵的极大无关组,则极大无关组列向量对应的约束力偶元素为求并结果。

(2) 约束力元素求并规则

在不考虑约束力空间位置的情况下,类比约束力偶元素求并规则,建立约束力元素求并规则一:在全局坐标系下,将所有分支约束参数中约束力元素表示的约束力作为列向量构成矩阵,通过线性列变换分析矩阵的极大无关组,则极大无关组列向量对应的约束力元素为部分求并结果。

在考虑约束力空间位置的情况下,建立约束力元素求并规则二:基于图谱法,在机构图上标记出约束力元素表示的力约束线,根据转动轴线与约束力相交或平行的位置关系,判断是否存在被约束的转动,若存在被约束的转动,则约束力元素求并结果包括被约束转动方向的约束力偶元素。

3.2 动平台约束参数

将过约束视为一般约束,避开对过约束进行特殊分析计算,根据运动空间与约束空间的对偶关系、转动轴线与约束力的位置关系,基于线性变换理论、图谱法,建立了分支约束参数的求并规则。

4 自由度分析实例

▲图3 3-RSR机构简图

基于运动求交与约束求并两种自由度分析方法的统一表达形式、各自求交规则以及不同使用场景,分析两者应用于不同运动与约束关系机构时自由度分析方法的有效性与差异性。

3-RSR机构如图3所示,机构的三条分支对称布置,球副连接的上下连杆长度相等。分支一坐标系o1-x1y1z1的原点与球副中心重合,x1轴沿转动副方向,z1轴竖直向上,y1轴由右手定则确定。其它分支坐标系建立方式与分支一相同。直线l1、l2、l3经过球心且沿各分支转动副方向。

4.1 运动求交分析

分支一螺旋系为

(9)

分支一的二次反螺旋系为

(10)

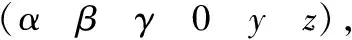
(11)

由于同三条分支完全相同,理可知在各分支坐标系系下,分支约束参数G2、G3为

(12)

在分支参数通过螺旋理论计算得到后,使用分支参数求交规则分析机构末端件自由度。

动平台参数GB为所有分支参数的交集,表示为

(13)

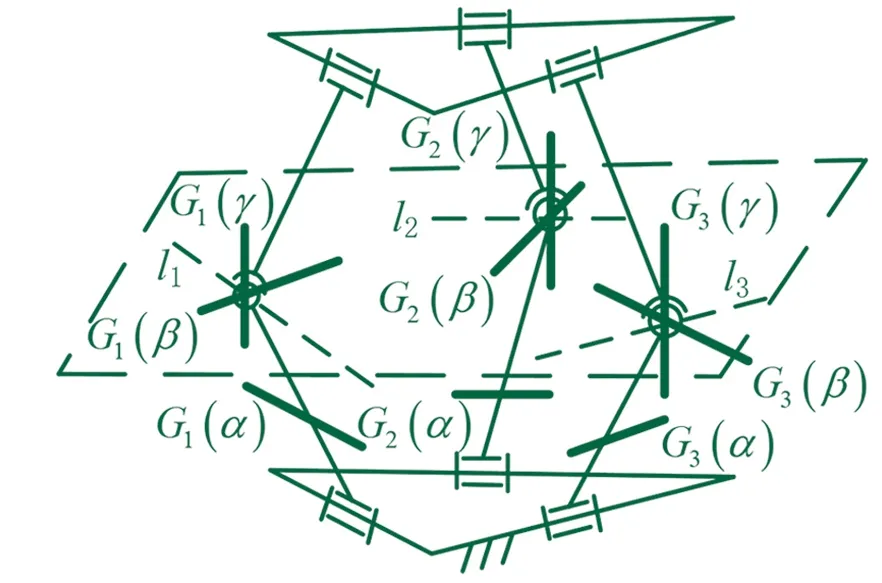
▲图4 3-RSR机构转动自由度线示意图

首先对角速度元素求交,各分支角速度元素对应的转动自由度线如图4所示。

转动自由度线G1(α)的位置任意,G1(β)经过直线l1,G1(α)与G1(β)能在平面l1l2上任意一点相交,可确定在平面l1l2上任意位置的径向线圆盘,同理G2(α)与G2(β)、G3(α)与G3(β)可确定在平面l1l2上任意位置的径向线圆盘。因此根据角速度元素求交规则2,交集空间为平面l1l2内的径向线圆盘,如图5所示。

▲图5 3-RSR机构转动自由度线交集空间

建立全局坐标系O-XYZ如图5所示,原点O位于定平台中心,Y轴平行于分支二的转动副,Z轴竖直向上。转动自由度线交集空间的基为平面l1l2内X、Y方向的转动自由度线,对应的角速度元素为α、β,因此角速度元素求交结果为且α⊂l1l2、β⊂

式中:v11、v21、v31分别沿各分支坐标系的y1、y2、y3方向。分支输出移动空间的交集为V1∩V2∩V3=V1∩(V2∩V3)。由交空间中向量表示法导出V1∩V2对应齐次线性方程组的系数矩阵为

(14)

(15)

以ε1为基建立运动空间Vε1,由交空间中向量表示法导出Vε1∩V3对应的齐次线性方程组的系数矩阵为

(16)

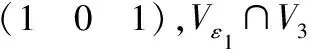
(17)

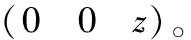
(18)

动平台参数GB是机构末端动平台自由度的符号解,表示动平台具有X、Y方向的转动及Z方向的移动,且转动轴线位于平面l1l2上。

4.2 约束求并分析

已知分支一螺旋系如式(24)所示,反螺旋为

(19)

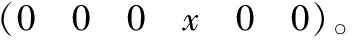
(20)

(21)

(22)

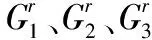
进行线性列变换,变换为

▲图6 3-RSR机构的力约束线图

在机构简图上表示约束力元素对应的力约束线,如图6所示。

(23)

(24)

根据式(18)与式(24)可知,使用约束求并方法得到的动平台参数GB与采用运动求交方法分析得到的结果一致。但采用约束求并的分析方法可直接得到此机构Z方向转动被约束的结论,且求解过程相对简单,这充分显示了约束求并思想在机构末端运动耦合、分支不明确以及分支数目多等情况下自由度分析的优越性。

上述典型机构自由度分析过程体现了运动求交与约束求并方法分别应用于同一约束性质机构时的差异性与适应性。结果表明,两者均以直观的符号作为表现形式,建立了逻辑严谨的规则,减小了符号运算难度,易于理解和使用;且验证了综合运动求交与约束求并方法面对复杂机构自由度分析的高效性及其避开过约束计算的有效性。

5 结论

(1) 针对因机构中过约束的存在而导致自由度的理论计算与实际运动出现矛盾的问题,提出一种综合运动求交与约束求并的自由度分析方法。借助数学符号描述了机构的运动特征和约束特征,明确了分支和动平台相关参数的表示形式,并阐述了自由度分析求解的基本步骤。

(2) 基于图谱法的线图元素清晰、直接的表达机构运动和约束的关系,从避开过约束的角度提出基于运动求交的机构自由度直接分析方法与基于约束求并的机构自由度间接分析方法,根据机构分支运动与约束的特点选择相应的计算方法。

(3) 统一了两种自由度分析方法的表达形式,建立了综合运动求交与约束求并的机构自由 度分析方法,并通过典型机构算例验证了其应用于复杂机构自由度分析的高效性和实用性。该方法计算简单,逻辑严谨,不仅为含过约束机构的自由度求解提供了思路,也为后续的机构综合研究提供了参考。