车辆转向梯形机构的一种新优化设计方法及其有效性验证

2023-07-25缪祥爱

机械设计与研究 2023年2期

缪祥爱, 张磊

(1.泸州职业技术学院智能制造与汽车工程学院,四川泸州 646000, E-mail: mouxa88@163.com;2.天津中德应用技术大学软件与通信学院,天津 300350)

车辆转向过程中,实际轨迹与理论轨迹之间的误差影响着行车的安全性和稳定性[1-4],而通过合理设计车辆转向梯形机构的相关尺寸,可以有效减小误差[5-8]。对于车辆转向梯形机构的优化设计问题,很多学者将其转换为一种带多约束条件的复杂非线性优化问题,而后通过一些智能优化算法进行求解,有效提高了优化设计的效果,提高了车辆行驶的安全性和稳定性。如相继提出的用于转向梯形机构优化设计的改进遗传算法[9]、反向认知果蝇优化算法[10]、具有均匀候选解机制的果蝇算法[11]、改进差分进化算法[12]、改进粒子群算法[13-14]等,都在一定程度上获得了更优的设计参数,减小了误差,提升了设计效果。

根据相关的研究结果可以看出,基于智能优化算法的车辆转向梯形机构优化设计已受到众多学者的关注。北方苍鹰优化算法[15](Northern Goshawk Optimization,NGO),是通过模拟北方苍鹰并于捕猎策略2022年刚提出的一种智能优化算法,在对不同类型基准测试函数以及几种工程设计问题中,展现出了较强的优化性能。目前,还未有关于该算法进一步研究发表。

为提高车辆转向梯形机构优化设计的效果,保证车辆行驶的安全性和稳定性,本文将NGO算法首次应用于车辆转向梯形机构的优化设计中,并通过途乐GRX、途乐GL和尼桑公爵3款车型的转向梯形机构优化设计实例对NGO的性能进行了验证和对比分析。

1 车辆转向梯形机构优化设计建模

为简便计算,在建立优化设计模型时,假设车轮为刚性车轮,不考虑车轮弹性侧偏的影响。

1.1 优化设计目标函数

图1为车辆转向机构的转向示意图。图1中:L为车辆轴距;M为左右两立轴之间的距离;R为外前轮的转弯半径;α和β分别为内前轮转角和外前轮理论转角;a为轮销间距。

▲图1 转向示意图

根据图1可得:

(1)

车辆在转弯过程中,当转弯半径得到最小时,则内前轮转角得到最大,即:

(2)

其中:Rmin为最小转弯半径。

图2为内转向轮转角为α时车辆的实际转向情况示意图:θ为转向梯形底角;β′为外前轮理想转角;m为梯形臂长度;N为辅助对角线长度;δ1、δ2为用于辅助计算的内角。

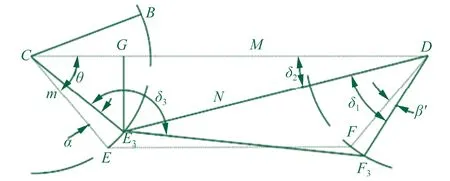
▲图2 实际转向示意图

根据图2可得:

N2=M2+m2-2mMcos(θ-α)

(3)

S2=(M-2Mcosθ)=N2+m2-2mNcosδ1

(4)

其中:S为横拉杆的长度。根据式(3)、式(4)以及图2可得:

β′=δ1-(θ-δ2)=δ1+δ2-θ

(5)

(6)

故可得β′为:

(7)

(8)

其中:X为优化变量,根据上述推导过程可知其由转向梯形底角θ和梯形臂长度m组成;αmax为内前轮转角的最大值;ω(αi)为加权系数,其不同取值反映的是不同外前轮理论转角和实际转角之间相对误差对转向性能的影响程度,其计算方式为:

(9)

1.2 约束条件

为保证梯形转向机构正常运转,还需要满足如下约束条件:

0.11M≤m≤0.15M

(10)

(11)

同时,为防止“死点”的出现,还应满足:

(12)

2 北方苍鹰优化算法

北方苍鹰是鹰科的一个中大型猛禽,主要分布在欧亚大陆和北美地区,主要以老鼠、兔子、松鼠等小型哺乳动物为食。它的捕猎策略包括两个阶段:

猎物识别与攻击、追逐及逃生。NGO算法就是模拟这一捕猎过程而提出的,其中猎物识别与攻击又可称为勘探阶段,追逐及逃生又可称为开发阶段。

在NGO算法中,北方苍鹰种群矩阵X可表示为:

(13)

其中:Xi为第i只北方苍鹰的位置,xi,j为第i只北方苍鹰在第j维空间的位置;N为北方苍鹰的种群数量;m为待求解优化问题的维数。

对于NGO算法求解的优化问题,针对优化问题设计的目标函数可以求得北方苍鹰的目标函数值,北方苍鹰种群的目标函数值矩阵可表示为:

(14)

其中:Fi为第i只北方苍鹰的目标函数值。

NGO算法中,北方苍鹰种群首先是进入勘探阶段。在这一阶段,北方苍鹰在搜索空间内搜索猎物是随机,目的是进行全局搜索,确定最优猎物区域。此阶段中,北方苍鹰的猎物选择和攻击行为可表示为:

Pi=Xk,i=1,2,…,N,k=1,2,…,i-1,i+1,…,N

(15)

(16)

(17)

北方苍鹰种群完成勘探阶段后,就进入开发阶段。在这一阶段,当北方苍鹰攻击猎物时,猎物会试图逃跑,就需要继续追击猎物,这种行为的模拟目的是进行局部搜索,保证局部搜索能力。此阶段中,北方苍鹰的攻击和追逐行为可表示为:

(18)

(19)

(20)

NGO算法主要流程如图3所示。

3 车辆转向梯形机构优化设计实例

3.1 优化设计实例

本文以途乐GRX、途乐GL和尼桑公爵这3款车型的转向梯形机构为优化设计对象,对所提NGO算法(流程见图3)的有效性进行验证,有关设计尺寸如表1所示。同时,还将NGO算法与目前已在转向梯形机构优化设计得到应用的反向认知果蝇优化算法[9](RCFOA)、改进差分进化算法[10](IGDE)和改进粒子群算法[13](IPSO)等方法进行对比分析。

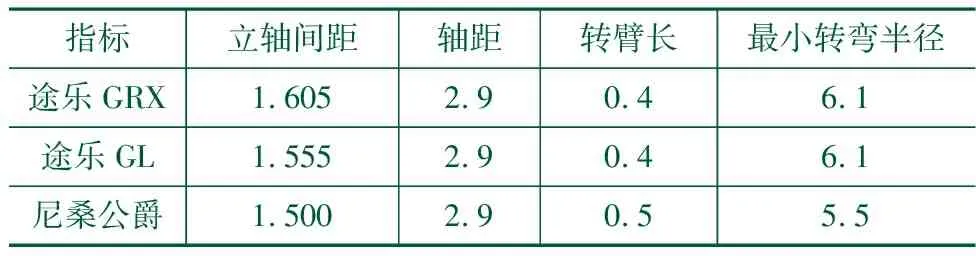
表1 部分设计尺寸/m

▲图3 NGO算法流程

3.2 优化设计结果分析

利用NGO、RCFOA、IGDE和IPSO这4种方法分别对3款车型转向梯形机构进行优化设计。4种方法在进行优化时,设置相同的参数,即种群规模N设置为40,最大迭代次数T设置为200,RCFOA、IGDE和IPSO需要设置的其余参数均按照原文献进行设置。同时,为消除随机误差对结果的影响,每种算法均独立优化计算20次。

由于途乐GRX、途乐GL和尼桑公爵这3款车型的优化设计结果基本一致,本文以途乐GRX转向梯形机构为例,对计算结果进行展示。4种方法独立计算20次后,得到途乐GRX转向机构的有关统计结果如表2所示。其中,最优值和最差值为20次计算中得到的目标函数值的最小值和最大值,平均值为20次计算所得目标函数值的平均,标准差为20次计算结果的标准差,平均耗时为20次计算的平均耗时,平均迭代次数为20次计算中每次计算得到最优值时需要的迭代次数的平均。表2中各算法所得最优值对应的优化迭代过程如图4所示。

表2 途乐GRX优化结果

▲图4 4种方法优化迭代过程

从表2中可以看出,对于最差值、最优值和平均值指标,均是本文所提NGO算法是最好的,特别是最差值指标,IGNO所得结果比其余3种方法所得最差值还要好,这说明IGNO的寻优性能更突出;对于标准差指标,IGNO所得结果的数量级为5,比其余3种方法分别提高了1、1和2个数量级,这说明NGO算法的计算稳定性更强;对于平均迭代次数和平均耗时指标,IGNO优化得到最优值时需要的迭代次数更少,计算耗时更短,较RCFOA、IGDE和IPSO在平均迭代次数上依次减少了7、18和11次,在平均耗时上依次缩短4.57 s、32.46 s、20.43 s。从图4中可以看出,NGO算法优化过程适应度值下降速度更快,且达到最优值时所需的迭代次数更少。

经4种方法分别优化后,3款车型的梯形臂长和梯形底角这两个待优化尺寸的优化值和理论值以及优化值与理论值的相对误差如表3所示。从表3中可以看出,对于3款车型而言,NGO算法得到的优化值与理论值更为接近,二者之间的相对误差比RCFOA、IGDE和IPSO均要小,特别是对于途乐GRX车型,NGO得到的优化值和理论值一致。表3的结果表明,NGO得到的优化值更接近与理论值,相对误差更小,优化结果更好。

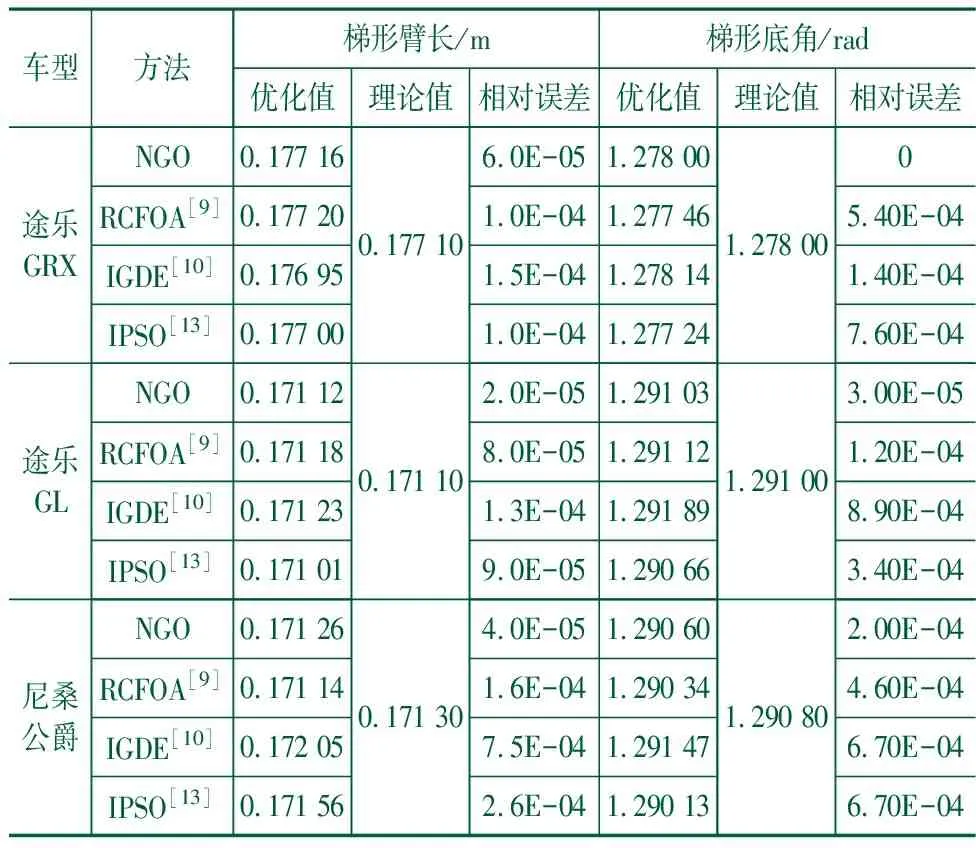
表3 优化尺寸与理论尺寸的比较

当内前轮转角连续取不同值时,将表3中途乐GRX车型基于NGO得到的梯形臂长0.177 16 m和梯形底角1.278 00 rad、基于RCFOA得到的梯形臂长0.177 20 m和梯形底角1.277 46 rad、基于IGDE得到的梯形臂长0.176 95 m和梯形底角1.278 14 rad、基于IPSO得到的梯形臂长0.177 16 m和梯形底角1.278 00 rad分别代入式目标函数式(8)中,可得途乐GRX车型转向梯形机构在转向过程中外前轮理论转角和实际转角的误差累积曲线如图5所示。

▲图5 途乐GRX转向过程相对误差累积曲线

从图5中可以看出,4种方法中,NGO算法得到的误差累积曲线总是处于最下方,即在最优尺寸下,NGO算法所得误差是最小的,此时车辆转向的安全性和稳定性最好,而RCFOA、IGDE和IPSO所得误差比NGO要大,车辆转向的安全性和稳定性不如NGO。

从图5中还可以看出,对于4种方法得到的误差累积曲线而言,均有一个相同的规律:在内前轮转角大致在1°～20°和31°～41°范围内时,误差累积曲线的斜率较大,误差累积增长较快;在内前轮转角大致在21°～30°和31°～41°范围内时,误差累积曲线的斜率较小,误差累积增长较慢。这一规律说明,在转向的开始阶段和结束阶段,转角的变化对车辆转弯的安全性和稳定性有较大影响,应在此阶段防止车辆出现侧滑;在转向的中间阶段,转角的变化对车辆转弯的安全性和稳定性影响较小。