纵轴式掘进机截割头振动特性分析

何 洋, 李晓豁, 席亚兵

(1.辽宁工业大学 汽车与交通工程学院,辽宁 锦州 121000,E-mail: heyang121000@163.com;2.广东文理职业学院 机电工程系,广东 湛江 524400;3. 三一重型装备有限公司 研究院,沈阳 110020)

纵轴式掘进机作为巷道掘进的关键设备,其性能好坏直接影响掘进生产率,但由于井下巷道作业环境恶劣、工作空间不断变化、煤岩赋存条件和载荷的复杂多变等因素影响,致使掘进机的截割载荷具有冲击性和随机性,导致截割头振动强烈,这不仅加剧了截齿磨损而且容易导致截齿断裂,降低工作效率,剧烈的振动还将损害机器零部件、液压及电气元件,降低机器各部件的使用寿命[1-3]。为此,国内外专家对于掘进机的振动特性进行了深入的研究。文献[4-8]通过实验方法,获取掘进机各部件的振动特征;文献[9]采用锤击法对掘进机的截割系统施加激振力,通过试验模态分析法,获得完整的截割部模态参数;文献[10]借助ADAMS建立掘进机刚柔耦合动力学模型,获取各部件的振动特征;文献[11]基于小波包分析方法分析三向截割载荷信号,获得截割载荷的能量频率。文献[12]基于Hilbert-Huang分析方法,借助Matlab获得振动信号的频谱特征和能量特征。

上述文献对研究掘进机的振动具有重要意义,但现有的方法主要基于实验和三维模型仿真的方法研究系统的振动特性,这是由于计算系统振动响应问题的经典方法需求解频响函数矩阵,计算繁琐且精度低。所以对于随机激励作用下,掘进机截割头振动特性的研究还不多见。现有的研究已证实掘进机钻进工作方式振动较大。为此,本文针对掘进机轴向钻进过程仿真计算和截割实验方法分析截割头的振动特性。

1 随机截割载荷计算方法

掘进机掘进巷道过程中,以截割头上任意参与截割的截齿为例,截齿受到煤岩施加的随机截割阻力Zi、随机牵引阻力Yi和随机侧向阻力Xi[13],如图1所示。

截齿的随机截割阻力Zi、随机牵引阻力Yi、侧向阻力Xi的瞬时值为

(1)

将参与截割的所有截齿受力沿截割头空间坐标(x、y、z)三个方向投影求和,则可得截割头的瞬时x、y、z三向随机截割载荷为

(2)

式中:θi为圆周角(°),θi=ωt;ω为角速度,rad/min;j为参与截割的截齿总数。

▲图1 截齿随机截割载荷模型

2 掘进机动力学模型

将截割头(m1)、悬臂(m2)和机体(m3)定义为质量均匀的质量块;截割头与悬臂、悬臂与机体、机体与底板间的刚度和阻尼分别为:k1m、k2m、k3m;c1m、c2m、c3m;m为x、y、z三个方向,整机的动力学模型见图2。

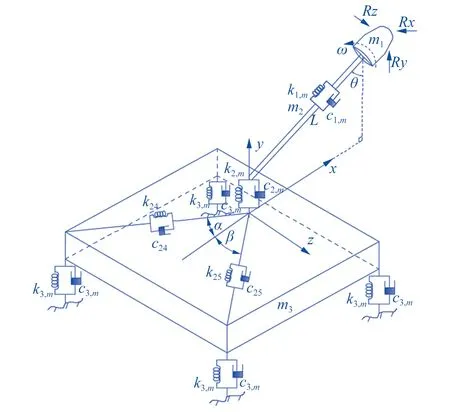
▲图2 纵轴式掘进机动力学模型

第二类拉格朗日方程为

(3)

系统x、y、z三个方向的动能T、势能V、能量耗散D为

x方向

(4)

y方向

(5)

z方向

(6)

将式(4)～(6)代入式(3),整理为矩阵形式,则纵轴式掘进机轴向钻进过程的微分方程为

(7)

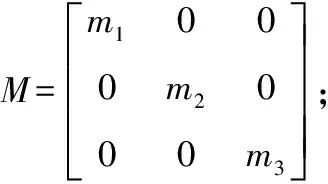
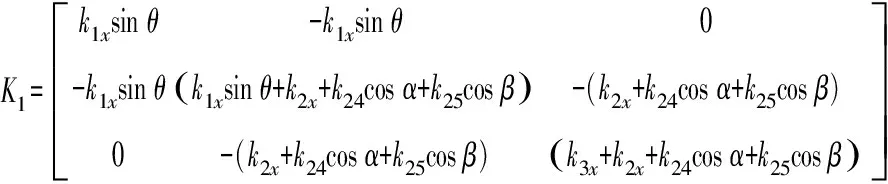
由于传统方法计算系统的响应谱,不可避免计算复杂的频响函数矩阵,耗时多、精度低、较为繁琐,故采用虚拟激励法计算响应谱[14],由

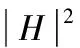
(8)

式中:H为频响函数;Saa为激励自功率谱;Sbb为响应自功率谱。

当平稳随机激励被简谐激励eiωt代替时,相应的响应为

y(t)=Heiωt

(9)

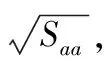
(10)

则响应谱为

(11)

显然,上述计算方法避免求解频复杂的响函数矩阵且简单、高效。

研究表明,随机截割载荷可视为宽平稳随机过程,载荷的均值近似为常值、方差与时间无关[15],其自功率谱密度序列为

(12)

式中:Tx(n)、Ty(n)、Tz(n)为三向截断随机信号的自相关函数;ω=2πk/N;k为任意整数。

由前述虚拟激励法原理,构造截割头(x、y、z)三向虚拟激励为

(13)

式中:p={1 0 0}T。

将式(13)代入式(7),有

(14)

令

(15)

(16)

(17)

将式(15)～(17)代入式(14),整理得截割头x、y、z三向位移响应功率谱为

(18)

(19)

(20)

3 仿真分析

相关参数:质量m1=1 051 kg,m2=2 415 kg,m3=56 534 kg;煤岩的抗截强度1 000 N/mm,截割头转速46 r/min,煤岩崩落角45°,煤岩脆性度2.5;采样频率fs=512 Hz。

3.1 截割头位移响应分析

利用Matlab汇编语言对系统仿真计算。图3(a)、(b)、(c)分别为截割头x、y、z三向位移响应随时间变化曲线。由图可见,响应变化具有随机性,截割头的y向峰值振幅最大,x向的峰值振幅最小,x、y、z三向响应均值依次为0.004 3 m,0.007 9 m,0.006 3 m。分析认为,整机系统的x向液压系统较多,刚度及阻尼系数较大,该方向支撑性较好;相反,y向是整机直接与底板接触,缺少液压支撑系统,加之截齿的截割阻力变化较大使得截割头该方向振动剧烈,因此可在悬臂两侧设置液压支撑油缸,可明显减小截割头的振动,提高截割效率。

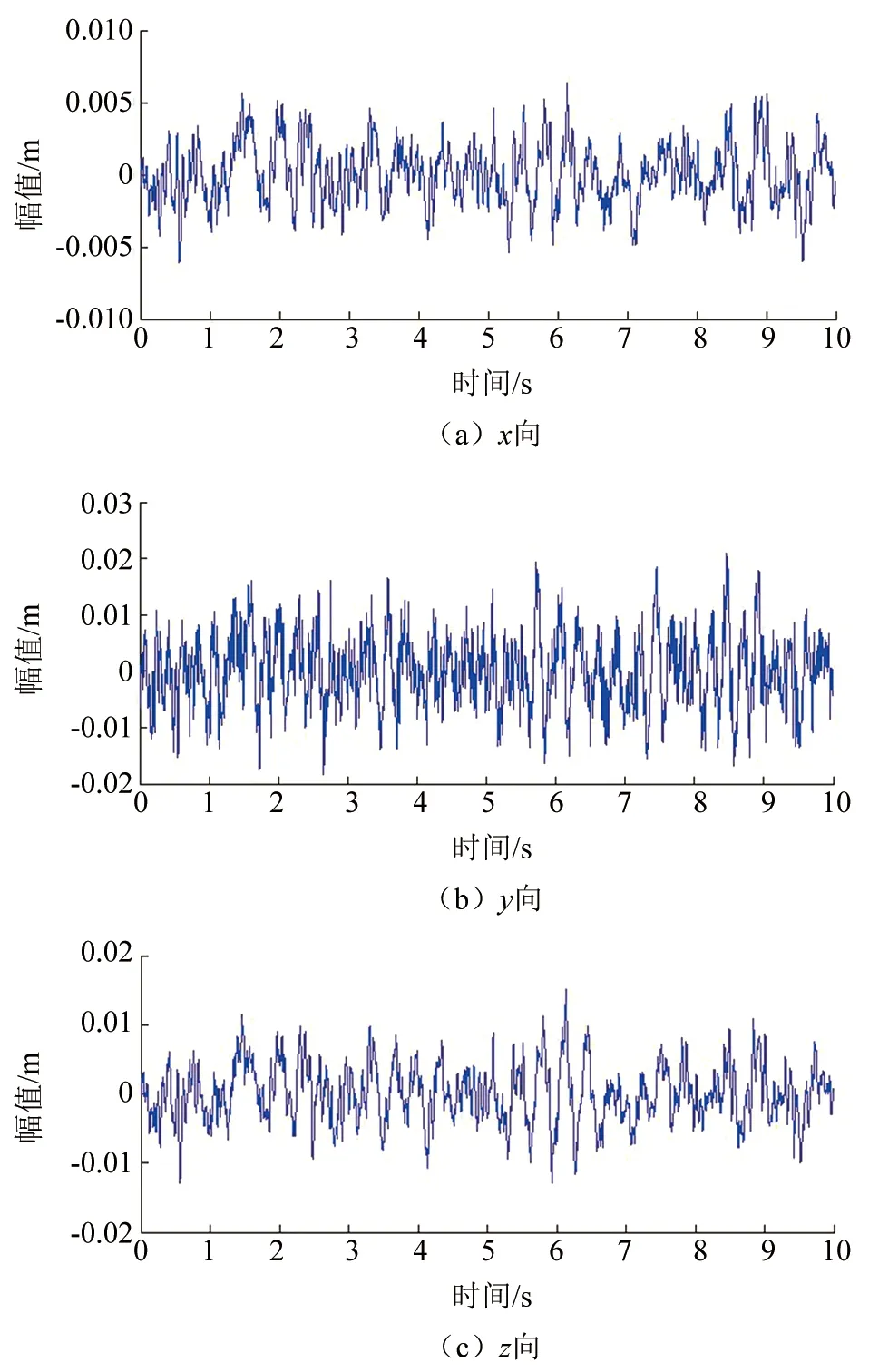
▲图3 截割头位移响应仿真结果

3.2 响应谱分析

图4(a)、(b)、(c)分别为该机截割头x、y、z三向位移功率谱密度曲线。由图可见,y向响应谱峰值集中在15 Hz内,两个较大峰值对应7.6 Hz和14.3 Hz附近;z向响应谱峰值仅出现在低频处4.7 Hz附近,而x向没有出现较大峰值,响应谱变化较平稳;由此可见,对截割头振动响应贡献较大的频率范围在(4～8)Hz内。

4 掘进机多刚体动力学仿真

纵轴式掘进机的组件主要包括(截割头、悬臂、回转台、液压油缸、铲板、行走机构等),采用Pro/e建立各部件三维模型,完成整机的装配并将其导入多刚体动力学分析软件ADAMS环境中,再添加材料属性、定义接触、约束等,相关参数见表1。采用文献[16]方法,由Matlab生成的激励信号文件据存放于ADAMS的控制器中,通过控制器加载截割头的随机激励,完成的纵轴式掘进机多刚体动力学模型,如图5所示。

表1 纵轴式掘进机多刚体动力学模型相关参数

▲图4 截割头三向位移响应功率谱

▲图5 纵轴式掘进机多刚体动力学模型

图6为仿真时间20 s、步频300,该机轴向钻进过程的截割头(x、y、z)三向位移响应变化情况,统计结果见表2。

表2 截割头位移响应统计值

▲图6 模型仿真的截割头位移响应

采用ADAMS/Vibration模块,对该机进行振动特性分析,得到截割头三维频响图,见图7。由图可见,功率谱峰值位于低频区域4 Hz附近,对应第4阶至第5阶模态,这理论计算结果基本吻合。

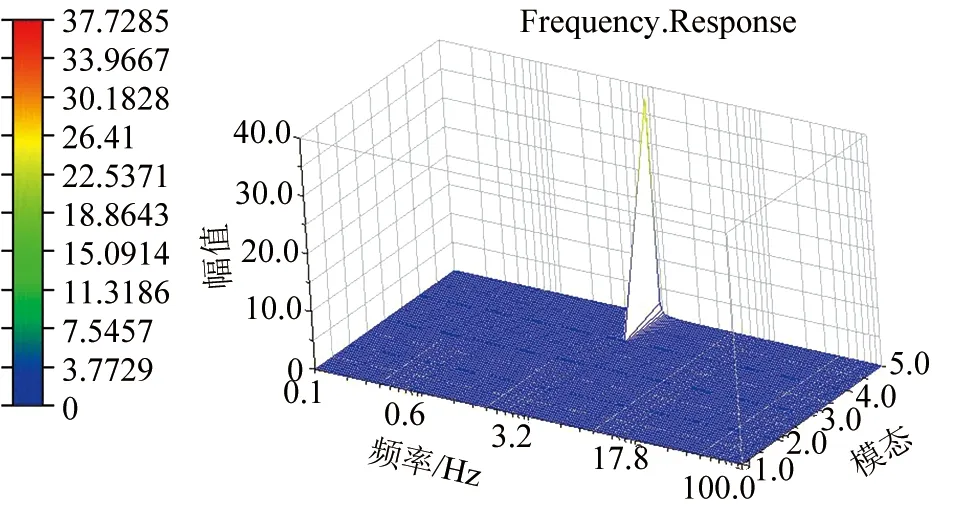
▲图7 截割头三维频响图

5 截割实验

5.1 实验测试系统

采用综合实验数据采集系统,实验数据采集流程如图8所示。该实验采集系统根据现场采集的实验数据,通过传感器测试信号,由无线变送器将数据传送至计算机,再由系统软件生成测试对象的振动特征。

▲图8 截割实验数据采集流程

▲图9 截割实验

截割实验对象是人工岩壁,如图9所示。其整体性质相对均匀,可以反映出掘进机在比较理想工作环境下的截割性能。该岩壁由混凝土和煤歼石颗粒配比堆砌而成,抗压强度(700～1 200)kg/cm2;普氏系数(f<10);规格(长×宽×高:9 m×8 m×3.5 m),截割头转速46 r/min,钻进速度1.2 m/min,深度为0.6 m。

5.2 截割头位移响应变化比对

图10(a)、(b)、(c)分为掘进机钻进人工岩壁时,截割头(x、y、z)三向的位移响应变化特征,其统计值见表2。

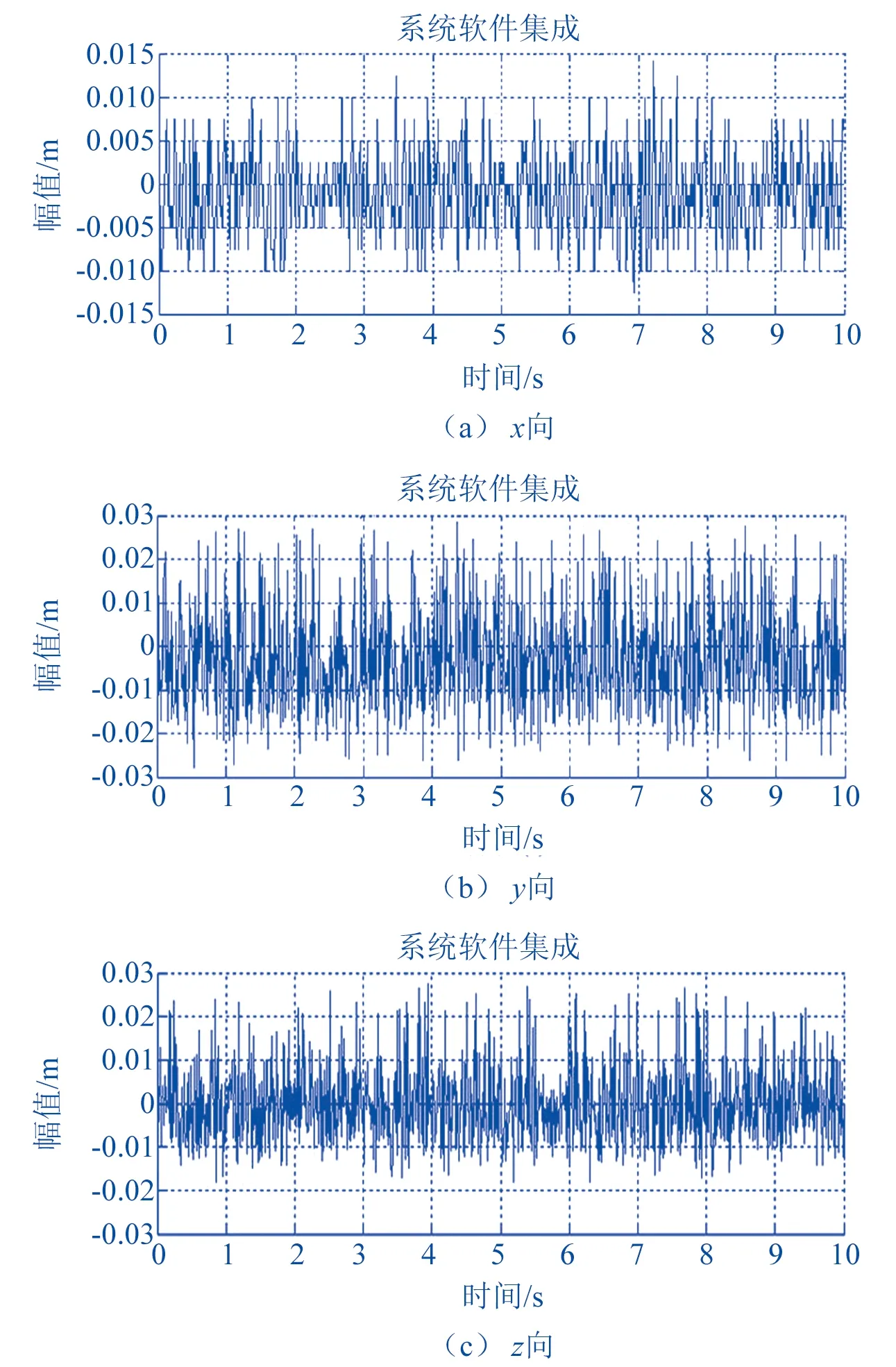
▲图10 截割实验的截割头位移响应

由图10实验结果可知,统计量中y向截割头响应峰值和均值最大,x向最小,这与仿真计算的结论一致。另外,表2的数据统计结果表明,动力学模型仿真结果和ADAMS模型仿真得到的截割头均值响应较接近,但两者均略小于实验结果,且均值误差范围在8.3%～18%之间。分析原因:① 由于截割实验使用的煤岩体为人工合成的岩壁,其各种性质和仿真计算的参数存在一定的偏差;② 截齿、截割头与岩体接触时具有较大摩擦力的影响;③截齿的排列方式、安装角度可能存在不合理因素,导致载荷波动大,振动剧烈。因此,仿真和实验的结果必定存在一些误差,但总体变化和规律基本一致。

6 结论

(1) 本文根据拉格朗日方程,结合虚拟激励法,建立纵轴式掘进机的动力学方程,通过对动力学模型的仿真分析,获得了随机激励作用下截割头的位移响应及响应谱,发现截割头y向响应值最大,且对系统响应贡献较大的频率范围在15 Hz内。

(2) 采用Pro/e和ADAMS联合仿真方法建立纵轴式掘进机的多刚体动力学模型,获取截割头的振动响应,为验证理论计算的可靠性和系统的参数优化奠定基础。

(3) 通过掘进机的截割实验,验证实了理论计算的可靠性,该方法为进一步研究掘进机各部件的振动提供了有效手段。