TBM面向节能的2K-H型行星轮系效率优化

2023-07-25徐尤南刘志强刘汕娟李明钦

机械设计与研究 2023年2期

徐尤南, 刘志强*,,2, 刘汕娟, 李明钦

(1.华东交通大学机电与车辆工程学院,南昌 330013, E-mail: xyn@ecjtu.jx.cn;2. 江西水利职业学院, 南昌 330013)

全断面硬岩隧道掘进机(Full face hard rock tunnel boring machine,TBM)是集机、电、液一体化的专用隧道掘进工程装备,广泛应用于岩石地层开挖[1-3]。但在实际施工中发现其动力损耗严重,如TB880E型TBM由8组功率高达435 kW电机驱动,将动力由传动系统传给刀盘,再传到刀具上破岩。若其以70 %额定功率掘进,切削功率每损失1%(相当于50 kW),在其2×104h工作寿命内累计能源动力损耗将达1×106kW·h。全国目前有数千台掘进装备工作,累计浪费总能量相当可观。另一方面,这些损耗的能量大部分将转化成热能,使洞遂中工作环境温度变高,为治理工作环境温度过高问题,还需要增加排气、降温等设施,消耗额外的能源动力。可见,工程上对于TBM节能施工具有实际需求。它将带来两方面的好处,一是施工中成本的节省,二是施工工作环境的改善。

行星减速器具有体积小,重量轻,传动比大及传动平稳等特点[4],且正朝着高速、高精度、高效率、低噪声、大功率方向发展[5],因而广泛应用于TBM传动系统。典型的掘进机传动系统由多组行星轮系及多级定轴轮系构成,其齿轮有的为内啮合,有的为外啮合,传动路径复杂。而在圆柱齿轮的动力传输过程中啮合效率占很大比例[6-7],啮合传动效率损失的减小,或是减少其动力损耗有效途径之一,尤其在高功率领域,效率更是重要的设计指标之一[8]。故本文以TBM行星减速器为研究对象,对其轮系啮合效率进行优化设计,以实现节能施工的工程目标。

为寻求提高行星传动效率的有效途径,国内外学者从不同领域,不同角度用不同方法对其进行分析及优化设计,如文献[9]考虑几何参数的影响,文献[10-11]采用虚功理论,文献[12]采用数值计算的方法等。一般而言,机械效率数值通常由试验方法确定,考虑几何参数的影响就是通过实验的方法,但在齿轮传动设计中,通过理论计算其啮合效率更为方便合理[13]。为提高齿轮的传动效率,国内外学者在其传动效率的理论数值计算方面做了大量的工作。圆柱齿轮传动效率计算方法通常是基于摩擦系数恒定和载荷沿接触线均匀分布的假设[14],如文献[13]通过积分法给出了齿轮副啮合效率的计算公式,文献[15]通过数值仿真建立直齿面齿轮啮合效率的计算模型,但过程较复杂且文中并未给出直齿轮计算方法。文献[16]采用摩擦功理论计算齿轮的效率,文献[17]在试验基础上给出啮合过程中效率损失的经验计算式,计算式简洁,初步筛选比较适用,但在一些特定场合并不适用;而且利用MATLAB拟合人字齿轮副滑动摩擦功率函数关系式,通过积分求出人字齿轮的滑动摩擦功率损失,过程复杂且未给出直齿轮计算方法。

综上所述,由于目前已公开的齿轮传动效率损失计算不便,或数值积分法计算过程复杂,或要求高精度时计算工作量大。为通过设计并优化TBM行星减速器轮系传动效率以实现节能目标,本文将采用作者自行推导的齿轮啮合效率计算式进行计算。在设计行星齿轮传动时,需要根据传动比确定各齿轮齿数,在确定行星齿轮传动的各轮齿数时,除满足传动比要求外,还需要满足与装配有关的条件,如同心条件、邻接条件、安装条件[18]等。而变位系数的优化选择问题,是在考虑一定的约束条件(如保证不发生根切、不发生径向干涉,不发生齿廓重叠干涉,保证必要的齿顶厚度和重合度等)下[19-21],遵循一定的分配原则(如等滑动率原则[22-23]减小齿轮的点蚀及磨损现象)进行各齿轮变位系数的分配,以达到齿轮最佳的工作性能。

本文以某型双级2K-H型TBM行星减速器为研究对象,以节能为设计目标(提高轮系啮合效率),研究其行星轮系变位系数及齿数的设计与优化方法。采用本文作者自行推导的齿轮副啮合效率损失计算式,建立其效率损失模型。利用2K-H行星轮系物理模型,推导其效率损失模型,进而进一步建立TBM行星减速器轮系效率损失模型,并以该减速器行星轮系为设计及优化实例,介绍其变位系数及齿数的设计与优化方法,以实现节能的工程目标。

1 效率损失模型

1.1 一对齿轮副啮合效率损失模型

1.1.1 齿轮啮合传动模型

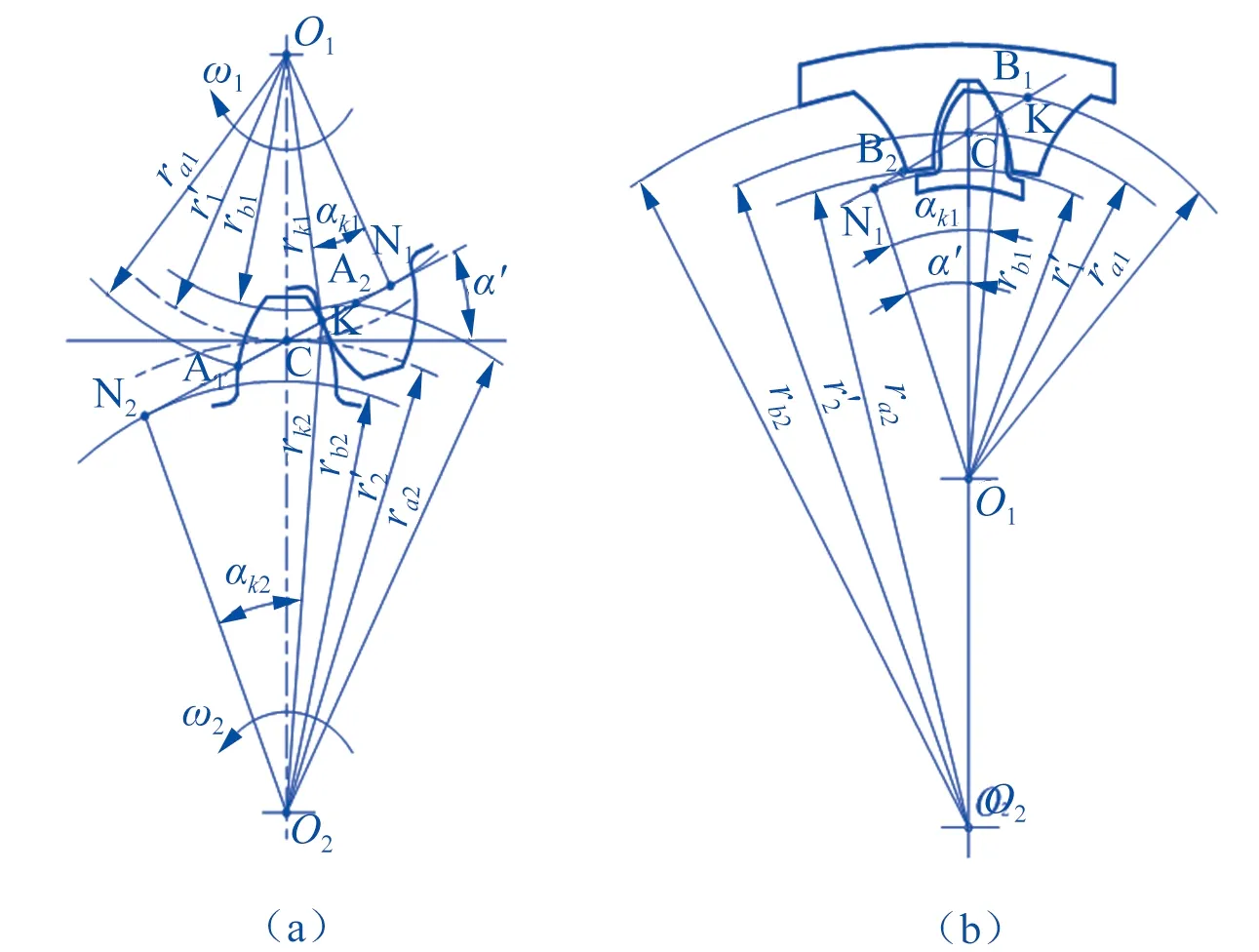
图1(a)、(b)分别是一对外啮合及一对内啮合齿轮副啮合的传动模型,基本参数如图所示。

▲图1 齿轮传动啮合模型

图1中,ωi为齿轮i的角速度方向,N1N2为理论啮合线,A1A2(B1B2)为实际啮合线,C为节点,K为啮合点,ra,r′,rb分别为齿顶圆,节圆,基圆,rK为渐开线在K点的向径,αK为渐开线在K点的压力角,α′为齿轮副啮合角。

1.1.2 一对齿轮副的基本啮合关系

设一对啮合齿轮副的标准中心距为a、实际中心距为a′、中心距变动系数为y、两齿轮的变位系数分别为x1,x2,其齿顶高变动系数为Δy,上述参数为下文变位系数优化的计算依据,此处先行给出。根据机械设计基本知识易知:

(1)

式中:z∑为齿数和;m为模数;符号“±”应根据内、外啮合关系选取,外啮合用上面符号,内啮合用下面符号(下同)。

结合无侧隙啮合方程,有:

(2)

式中:α′为实际啮合角,利用无侧隙啮合方程求解,α为标准压力角。

由此,可得中心距变动系数y:

y=(a′-a)/m

(3)

根据无侧隙啮合条件,有:

(4)

式中:inv为渐开线函数。

1.1.3 一对啮合齿轮副的部分重合度参数

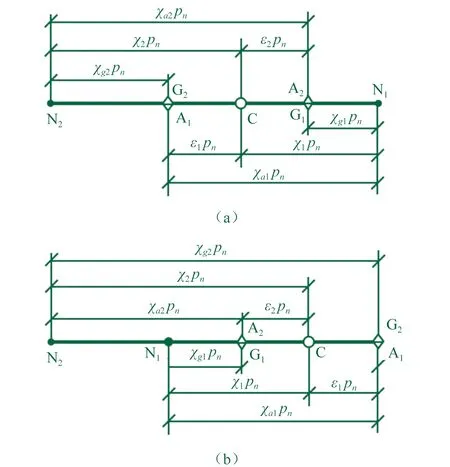
部分重合度是下文计算齿轮副啮合效率的重要参量。图2(a),(b)分别是一对外啮合及一对内啮合齿轮副啮合状态下的简化模型。

▲图2 齿轮啮合传动简化模型

图2中N1和N2分别为两齿轮的啮合极限点,节点C将其分为CN1和CN2两个部分,实际啮合线段为A1A2,其两端点A1、A2分别对应于齿顶处的啮合点,G1、G2则分别位于齿根部对应于另一齿轮齿顶处的啮合点(本文为叙述方便,将其称其所在的圆为类齿根圆),ε1和ε2为对应的部分重合度。且图2(a)得外啮合部分重合度计算式为:

(5)

式中:χ为法节比,其定义为法线长(齿廓曲线对应点曲率半径ρ)与法节长度Pn比值,故齿廓曲线K点处法节比χk为:

(6)

当某齿轮齿顶越过节点处于另一侧时,部分重合度将为负值。故对于其重合度ε外啮合按式(7)计算:

ε=ε1±ε2

(7)

式中:当齿顶越过节点与类齿根处于节点同侧取“-”号,否则“+”号(下同)。

同理,由图2(b)得内啮合部分重合度及重合度分别按按式(8)和式(9)计算:

(8)

ε=ε2±ε1

(9)

1.1.4 一对啮合齿轮的啮合效率损失计算模型

如图1所示的一对齿轮,其啮合效率损失计算模型,将采用本文作者自行推导的计算式(10)进行计算:

(10)

式中:Δηz为啮合效率损失,f为摩擦系数,εΣ为综合重合度,zΣ为综合齿数,且:

(11)

按文献[23]建议齿轮的平均摩擦系数为0.03～0.07,本文计算时取其均值f=0.05。

1.2 TBM行星轮系啮合效率损失计算模型

TBM减速器行星轮系通常由多级2K-H(NGW)行星轮系串联组成。且根据总传动比要求及预先分配好的传动比,可把多级传动分解为单级传动分别加以优化,简化优化过程。

1.2.1 2K-H行星轮系物理模型

单级2K-H行星减速器轮系由太阳轮z1、行星轮z2、内齿圈z3及行星架H组成(如图3(a)所示)。z1,z2组成外啮合齿轮副z1-z2,z2,z3组成内啮合齿轮副z2-z3,行星架H作为输出,各齿轮角速度为ωi(i=1,2,3),行星架H角速度为ωH。

分析2K-H行星轮系效率时,采用反转法将其转化为定轴轮系,转化机构如图3(b)所示。

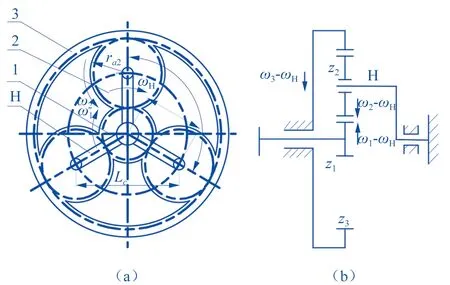
▲图3 2K-H行星轮系及其转化机构

1.2.2 2K-H行星轮系啮合效率损失计算模型

如图3(a)所示2K-H行星轮系由一对外啮合及一对内啮合齿轮副组成,其轮系啮合效率损失计算式与式(10)～(11)有关。转化后的轮系示意图如图3(b)所示,其中中心轮3为转化后输出构件,中心轮1仍为输入构件。实际上,机械中的摩擦损失功率主要取决于各运动副中的作用力、运动副元素间的摩擦因数和相对运动速度的大小。而行星轮系的转化轮系和原行星轮系的上述三个参量除因构件回转的离心惯性力有所不同外,其余均不会改变。因而,行星轮系与其转化轮系中的摩擦损失功率(主要指轮齿啮合损失功率)应相等。

根据图3(b)分析易知,转化后,轮系的效率损失率为:

Δηe=Δη12+Δη23

(12)

式中:Δη12和Δη23分别为转化后齿轮副z1-z2和齿轮副z2-z3传动效率损失,按式(10)计算。

显然,转化后轮系的功率损失为:

(13)

转化前,轮系的功率损失为:

ΔW=Δηm1ω1=Δηm1i1HωH

(14)

则据ΔWe=ΔW得周转轮系传动效率为[12]:

Δη=(1-1/i1H)·(Δη12+Δη23)

(15)

此式即为本文所采用的单级2K-H行星轮系啮合效率损失计算模型,式(13)～式(15)推到过程可参阅文献[16]。

1.2.3 TBM行星减速器轮系啮合效率损失模型

▲图4 双级2K-H型行星减速器机构简图

图4为现有某双级2K-H型型TBM行星轮减速器的机构简图,图4中,J为输入电机,第Ⅰ级2K-H行星减速器轮系由z1,z2,z3及H1组成,其中z1,z3为中心轮,z2为行星轮,H1为其行星架。第Ⅱ级2K-H行星减速器轮系由z4,z5,z6及H2组成,其中z4,z6为中心轮,z5为行星轮,H2为其行星架。

根据式(15)建立的单级2K-H行星轮系啮合效率损失计算模型,得图4中双级2K-H行星减速器轮系啮合效率损失计算(16)。

(16)

式中:ΔηI为第一级2K-H行星轮系效率损失,其值按式(15)计算,ΔηⅡ为第二级2K-H行星轮系效率损失,只是齿轮副z1-z2和齿轮副z2-z3由齿轮副z4-z5和齿轮副z5-z6进行相应替换。

故图示TBM行星减速器轮系啮合效率损失计算为:

Δη∑=1-(1-ΔηⅠ)(1-ΔηⅡ)≈ΔηⅠ+ΔηⅡ

(17)

此式即为本文所采用的双级2K-H型行星减速器轮系啮合效率损失计算模型。

2 TBM行星轮系优化方法

本文以图4所示的双级2K-H型行星减速器轮系为研究对象,设各齿轮副之间摩擦系数为f,齿轮zi对应变位系数为xi(i=1,2,…,6)。拟采用变位系数和齿数的两阶段优化方法,通过本文所述方法优化其变位系数及齿数,使其效率损失最小化,达到节能的目的。

2.1 齿数变化与效率损失规律分析

TBM行星轮减速器共有两级2K-H型行星轮系计6个齿轮构成,其设计变量为zi(i=1,2,…,6)。图5是第一级2K-H型行星轮系齿数变化下中心轮z3与其效率损失关系图。

从图5可以看出,随着齿数增加,轮系效率损失呈下降趋势,说明增加齿轮齿数可有效减小轮系的效率损失(齿数增加,重合度增加,参与啮合齿数增加,啮合效率提高),但齿数增加也会使机构整体尺寸增加。需要说明的是,图5中z3的数值需满足行星轮系的几何计算关系,该部分内容在2.2节介绍。且z3的取值范围旨在研究齿数变化对效率的影响,而TBM工作空间狭小,故齿数增加只能在小范围内波动,故限定齿轮z3和z6的最大齿轮的上限是分别是90和60。

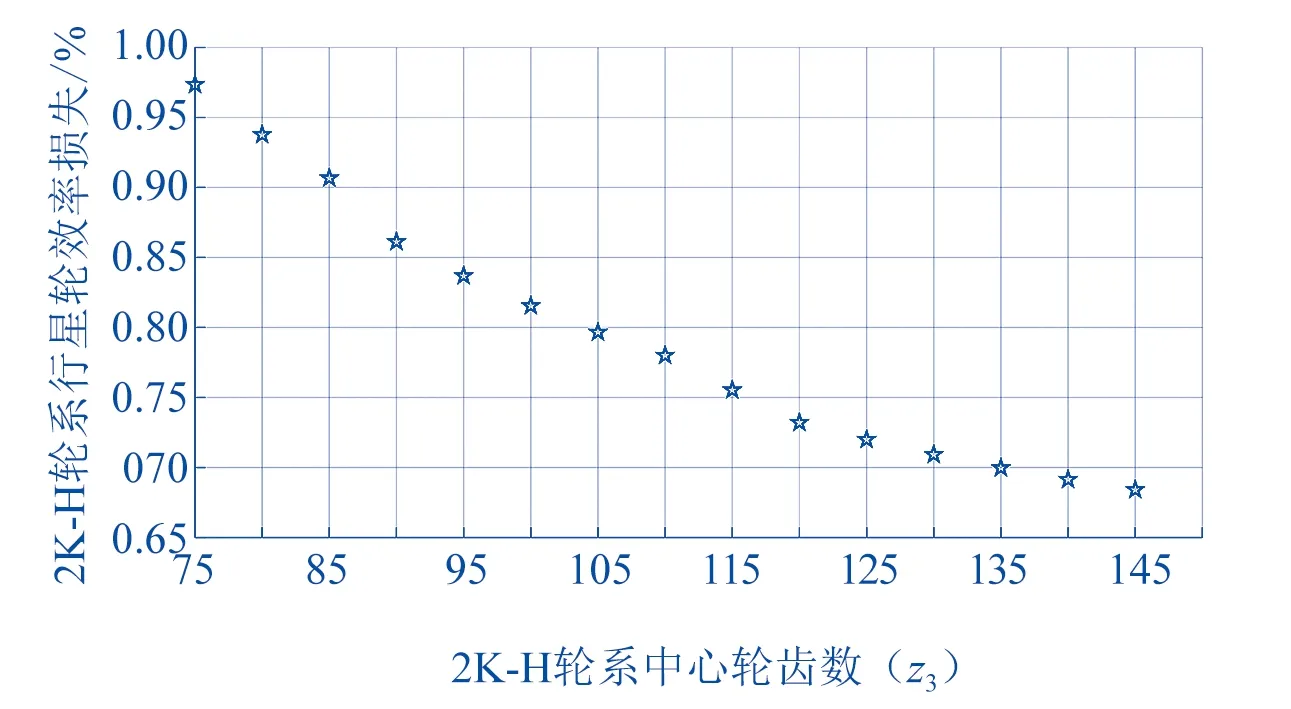
▲图5 齿数变化下2K-H行星轮系效率损失

2.2 齿数可行域分析

单级2K-H行星轮系齿数需要满足如传动比条件、同心条件、邻接条件、安装条件等一系列约束条件,其中首要条件是传动比条件。在对传动比进行分析时,需要采用反转法将其转化为定轴轮系,转化机构如图3(b)所示。

易知其传动比为:

i1H=-(1+z3/z1)

(18)

式中,i1H为2K-H行星轮系实际传动比。

应当指出的是,对于行星传动系统,速比设计对传动效率具有最重要的影响,大速比下甚至可能自锁,由于篇幅限制,本文不做具体分析。但为避免自锁现象的产生,本文将在现有方案的速比下一定波动范围内进行设计,设传动比误差为5%。

为保证2K-H行星轮系正确装配,两个中心轮(齿轮1和齿轮3)与系杆H三个基本构件需满足同心条件。其等价条件为:中心轮1—行星轮2的实际中心距,与行星轮2—中心轮3的实际中心距必须相等,因而有:

(19)

考虑采用变位齿轮可配凑中心距,在满足等中心距的基础上齿轮z3允许有2个齿数的误差(标准齿轮应满足齿数和相等)。

行星齿轮传动时为了进行功率分流,提高其承载能力,同时也为了减小其结构尺寸,通常在中心轮1、3之间,均匀、对称地设置nK个行星轮。为了使各行星轮之间齿顶不产生相互碰撞,必须保证它们齿顶之间在其连心线上有一定的间隙,即两相邻行星轮的顶圆半径之和应小于其中心距LC,此即为其邻接条件。

(20)

式中:nK为行星轮个数,LC为相邻两个行星轮中心之间的距离(图3(a))。本文取nK=3时,邻接条件满足,故消除一个约束条件。

另外,要使nK个行星轮能均匀装入,并保证与两中心轮正确啮合且没有错位现象,两齿轮齿数和必须是nK的整数倍,该关系即为装配条件,转化为相应的数学式可表示为:

rem(z1+z3,nK)=0

(21)

式中:rem为求余函数。

得齿数变化约束条件为:

(22)

式中:不等式约束1和2为最大齿数限制,不等式约束3为传动比误差限制(齿数变化下允许5%的传动比误差限制),不等式约束4和5为行星轮齿数约束,等式约束1和2为装配条件约束,由式(21)转化所得。

得双级2K-H型行星减速器轮系低速级及高速级齿数可行域如图6所示。

▲图6 双级2K-H型行星减速器轮系齿数可行域

2.3 变位系数变化与效率损失规律分析

在齿数不变的前提下,可对变位系数进行优化。对单级2K-H行星轮系而言,齿顶高系数、齿顶隙系数、分度圆压力角选为设计常量,中心距a12,a23及变位系数x1,x2,x3为设计变量,其他参数均作为中间变量处理。

设计过程中注意正确啮合条件及无侧隙啮合方程,中心距a12,a23必需相等,据此,可设置中心中a作为其共同的中心距,并以其作为设计变量,从而消除一个设计自由度。

另外,齿轮2一方面与齿轮1作外啮合,另一方面与齿轮3作内啮合,行星轮z2作为齿轮副z1-z2和齿轮副z2-z3的连接桥梁,在优化过程中,x2将是一个重要的优化变量。故其变位系数x2可作为独立设计变量。再根据正确啮合条件(式(3))及无侧隙方程(式(4)),由中心a及齿轮2的变位系数x2,即可得到齿轮1变位系数x1和齿轮3变位系数x3,从而再消除两个设计变量。且考虑变位系数数值较小,中心距数值较大,用中心距变动系数y相应替代。故在齿数已知时,对单级2K-H行星轮系进行效率优化的设计变量为中心距变动系数y和齿轮2的变位系数x2,以现有设计第一级齿数参数为例(z1=17,z2=34,z3=85(下同)),得该单级2K-H行星轮系啮合效率损失如图7所示。

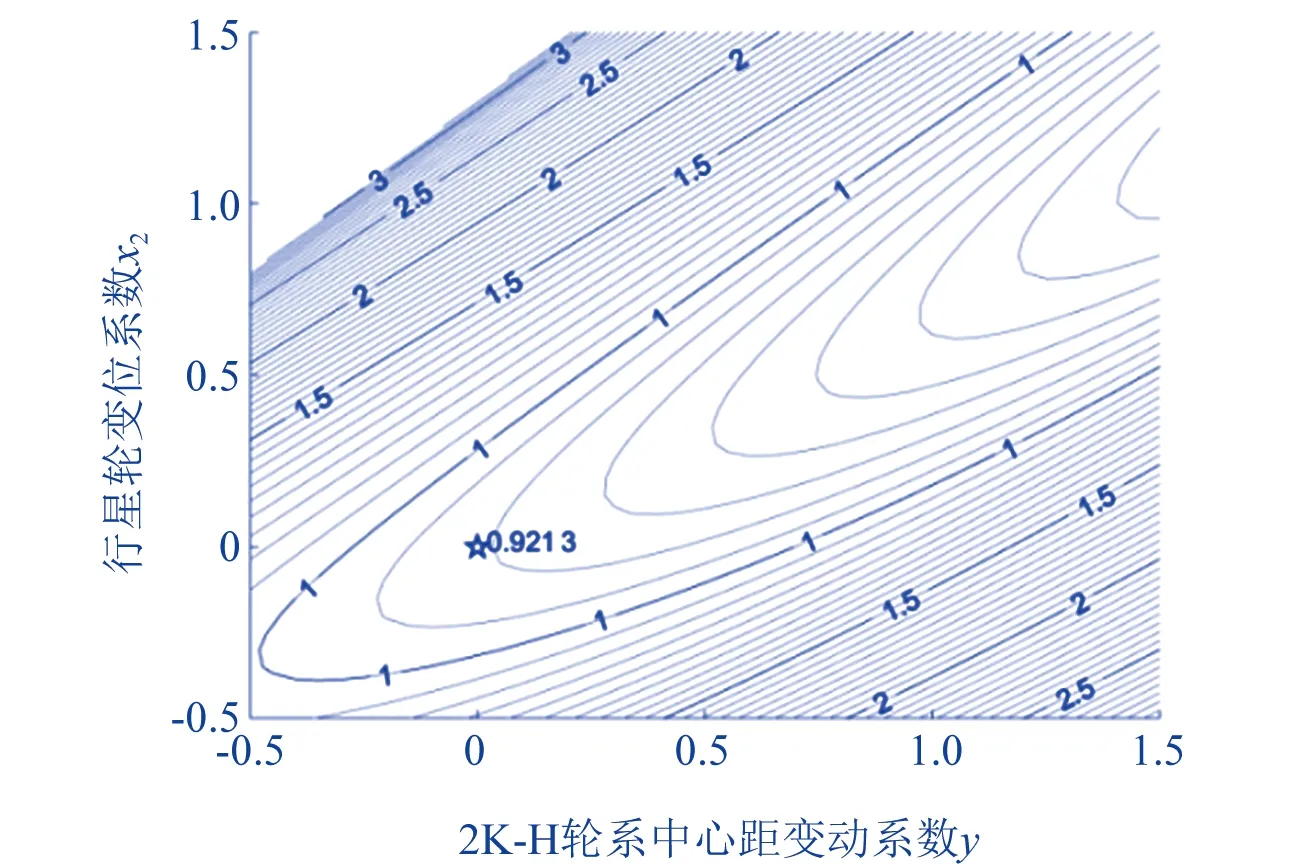
▲图7 单级2K-H行星轮系啮合效率

图7中,等值线数值表示轮系啮合效率损失百分比,空白区域为非可行域。读图可知,在不变位的情况下,轮系效率损失为0.921 3%,而效率损失最小点为等值线曲率中心处,而不由中心距变动系数y或齿轮2的变位系数x2单一决定,故合理分配y和x2的取值,才能取得更理想的优化效果。

2.4 变位系数可行域分析

已知齿数进行变位系数分析过程中,需要考虑外齿轮齿顶厚(Sa)、内齿轮齿槽宽(Ef)、最大滑动率(ξmax)及齿廓重叠干涉,齿廓径向干涉等系列参量,具体来说:

一对外啮合齿轮的大、小齿轮及一对内啮合齿轮的小齿轮,其最小变位系数受根切条件限制,最大变位系数受齿顶变尖条件限制,即:

(23)

式中:Samin,xmin分别为外齿轮最小齿顶厚及最小变位系数,且:

而一对内啮合齿轮的大齿轮,其最大变位系数受齿根基圆半径大小限制,最小变位系数则受齿根处齿槽变尖条件限制,即:

(24)

式中:Efmin为内齿轮最小齿槽宽,且:

当内啮合的行星轮2与外中心轮3齿数差较小时,内齿轮在装配时将不能沿径向安装到位,从而产生径向插入干涉。其不产生径向插入干涉条件为:

(25)

式中:u为齿数比,ν=1/u为其反比(下同),且

当内啮合的行星轮2与外中心轮3齿数差较小时,结束啮合的行星轮齿顶在退出内齿轮齿槽时,两者的齿廓将会重叠,从而产生齿廓重叠干涉。其不发生齿廓重叠干涉的条件为[7];

(26)

径向插入主要影响安装方式,不影响安装后齿廓的啮合运动,是许可的。齿廓重叠干涉则会影响齿廓的啮合运动,是绝对不许可的。实际计算时,为便于观察其规律性,将用等价的法节比,替代干涉量,即:

(27)

此外,齿轮实际啮合齿廓为渐开线,因而在分析齿廓啮合干涉时,需要考虑渐开线起点处的曲率半径,对于外齿轮(i=1,2),假定采用齿条刀具加工,可推知:

(28)

对于内啮合齿轮,其整个齿廓均为渐开线,因而无需计算。

对于内啮合齿轮对z2-z3,为避免行星轮z2过渡曲线与内齿轮z3齿顶发生干涉,内齿轮应满足的条件是极限啮合点不能超过实际渐开线起始点,即:

Δχ3=χ2-χρ2-ε3≥0

(29)

式中:部分重合度ε3与内齿轮齿顶圆半径ra3有关,齿轮2渐开线起点处法节比χρ2按前文所述计算。

同样,外啮合齿轮对z1-z2一个齿轮的齿顶也可能与另一个齿轮齿根处的过渡曲线干涉(由于齿轮根部的一段齿廓是由刀具齿顶圆角加工出来的过渡曲线,当此过渡曲线与另一齿轮的渐开线齿廓接触时不能保证正确啮合),且有:

(30)

需要注意的是式(29)与(30)节点法节比及部分重合度,应按所在的齿轮对分别计算。

一对啮合齿轮最基本的性能即其重合度,该参数反映其连续平稳传动性能,故:

(31)

式中:ε12和ε23分别为齿轮副z1-z2和齿轮副z2-z3的重合度,εmin为最小重合度,本文取值1.1。

如前所述,相互啮合的两齿轮应尽量保持相等的相对滑动速度。对于z1与z2组成的外啮合,其最大滑动率计算式为[21]:

(32)

对于z1与z2组成的内啮合,其齿轮最大滑动率计算式为:

(33)

得变位系数约束条件为:

(34)

式中:不等式约束1,2,…,6为单级2K-H行星轮系齿轮1,2,3的变位系数最小值和最大值约束,由式(23)和式(24)转化所得:不等式约束7为径向插入干涉约束,由式(25)式(26)转化所得:不等式约束8为齿廓重叠干涉式,由(26)转化所得:不等式约束9,10,11为过渡曲线干涉约束,由式(29)和式(30)转化所得:不等式约束12,13为重合度约束,由式(31)转化所得:等式约束1,2为等滑动率约束,可由式(32)和式(33)转化所得。

3 优化模型

3.1 变位系数优化模型

综上所述,在确定齿数的前提下,若不考虑等滑动率原则,得单级2K-H行星轮系效率最优化模型为:

(35)

优化结果如图8所示。

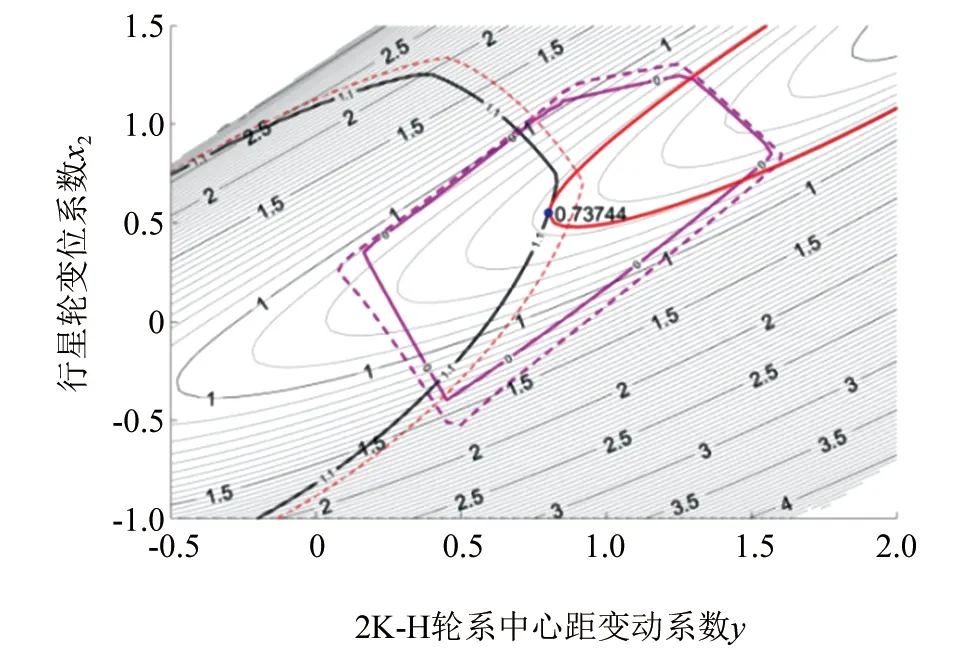
▲图8 不考虑等滑动率优化结果

图8中,相近的一条实线与一条虚线形成一个约束,所述的实线为不等式约束界面,虚线表示非可行域,封闭曲线为约束1～11形成可行域,半封闭曲线为约束12～13形成可行域,若不考虑等滑动率因素,效率最优点在0.737 4处,若考虑等滑动率因素,则在式(35)基础上增加等滑动率条件约束,可在图8的基础上添加等滑动率曲线进行分析,如图9所示。

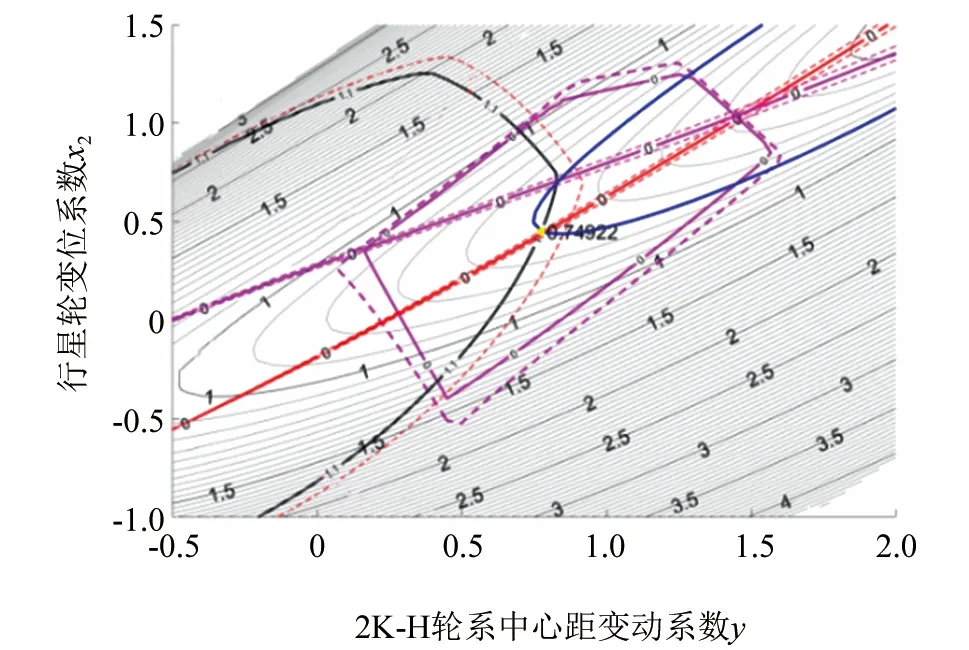
▲图9 考虑等滑动率优化结果

图9中,一条实线外加两条虚线表示等式约束曲线,所述的实线为等式约束界面,虚线表示非可行域,从图中可知,等滑动率交点处于基本可行区间之外,显然没有最优解。由于内啮合齿轮副效率损失小于外啮合齿轮副,故不能同时对内啮合及外啮合进行等滑动率进行考虑,而外啮合相对内啮合效率损失较大,故只考虑外啮合齿轮对最大滑动率因素(图中有数值标明等式约束曲线为外啮合等滑动率曲线,无数值标明等式约束曲线为内啮合等滑动率曲线)。得确定齿数的前提下,考虑等滑动率原则,单级2K-H行星轮系效率最优化模型为:

(36)

同理可得,现有参数下低速级变位系数优化结果如图10所示。

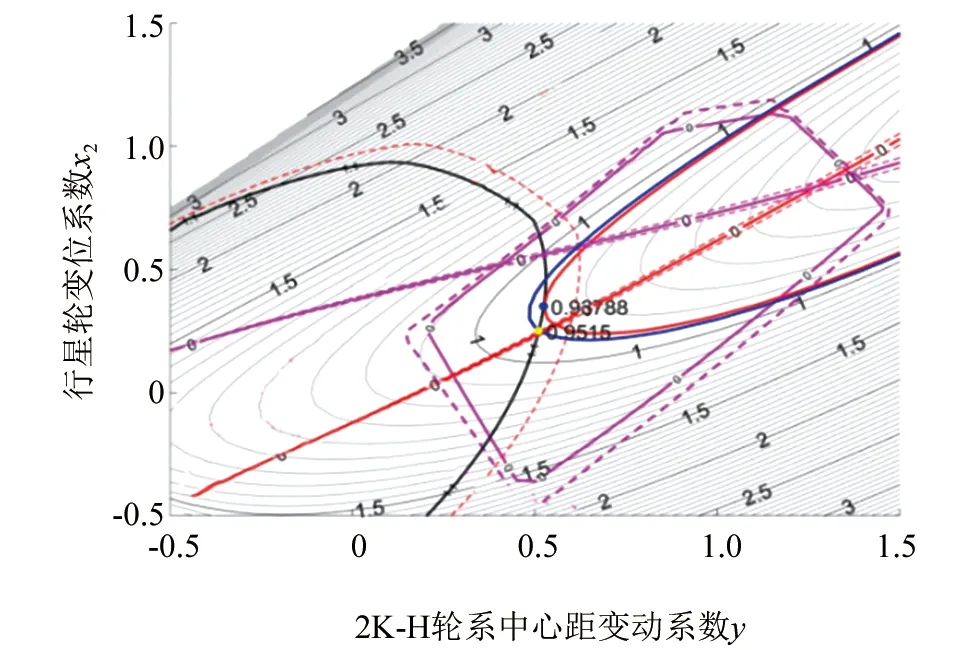
▲图10 低速级变位系数优化结果

3.2 齿数优化模型

齿数变化下,由双级2K-H型TBM行星减速器轮系效率损失计算式(17),得其效率损失最小化优化模型如下:

(37)

式中:z的取值范围为图6所示可行域,即设计约束按式(22)计算,且:

(38)

为高速级2K-H型轮系优化结果,当不考虑等滑动率原则时,约束条件为式(35),考虑等滑动率原则时,约束条件为式(36)。

(39)

为低速级2K-H型轮系优化结果,设计约束同上。

可见,对齿数优化相当于两阶段优化方法,其中,第一阶段对变位系数进行优化,第二阶段对齿数优化。

4 优化结果

借助约束图谱验证优化结果的可行性,得两阶段优化后高速级和低速级约束图谱分别如图11(a),(b)所示,且将现有齿数经变位系数优化后的效率损失最小值及其齿数和变位系数两阶段优化后的效率损失最小值汇集于下表。

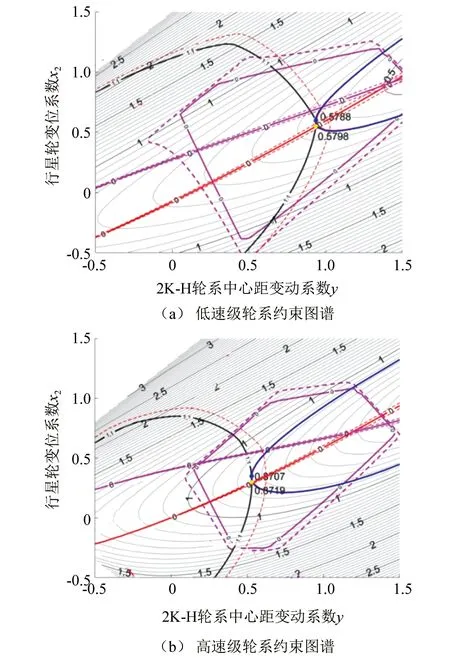
▲图11 优化结果约束图谱

优化结果对比表

(40)

(41)

表中,现有齿数作变位系数设计实例中,在不考虑等滑动率情况下,效率损失1.685% ,考虑等滑动率情况下,效率损失1.720%。而经过齿数和变位系数的两阶段优化,对应结果分别为1.415%和1.532%,效率损失减少分别为0.270%和0.188%。显然,其绝对值较小,但相对效率损失减小16.026% 和10.954%,正如前文B880E型TBM切削系统相关数据,若效率损失绝对值减小按0.2%计算,在其2×104h工作寿命内累计能源动力损失减少达2×105kW·h,能量节约总量相当可观。