基于KPCA和PSO-SVM方法的齿轮裂纹故障信号诊断

于松鹤, 王亚楠, 路泽永, 王康康, 李 峰

(1.河南开放大学 信息工程与人工智能学院,郑州 450000,E-mail: yusonghe2022@163.com;2.河南开放大学 机电工程学院,郑州 450008; 3.河北石油职业技术大学 河北省仪器仪表产业技术研究院,河北 承德 067000; 4.河南科技大学 机械工程学院,郑州 460000)

齿轮属于一种重要的机械动力传输部件,在各类传动系统中发挥了关键作用,对于促进机械工业系统技术进步起到了显著影响,在高铁动力系统、航空系统、精密机械控制领域获得广泛使用[1-2]。齿轮系统在运行过程中进行传动时,交变载荷会造成齿轮综合性能的恶化并出现寿命明显减短的情况,甚至还会造成整体设备停机的后果[3]。为消除齿轮故障因素引起的系统控制精度变化,应开发一个高效的诊断模型达到齿轮故障的准确诊断功能,保证完成机械设备的高效维护[4-5]。

为了全面诊断齿轮故障,应综合分析特征提取和分类的过程。现阶段,已有许多文献报道了时频域故障诊断方面的内容,形成了短时傅里叶变换、小波数据分解、经验模态分析等多种形式[6-8]。以上所述方法分别具备各自特征,STFT具备固定尺寸和外形,并不能实现高低频参数的精确调节;EMD和EEMD之间存在模态混合的情况,对其进行小波分析时无法获得准确的基函数;VMD则容易产生明显的边界影响[9-10]。现有信号处理模式拥有各自特点,提取出的特征参数也具有明显差异性,可以结合前期经验设置最优特征参数。由于相关系数方法对于分析结果具备较大的可行性,可以综合考虑故障特征与种类相关性条件选择故障特征[11]。按照以上处理方式确定与故障类型存在紧密关联的特征参数,而实际采集得到的故障数据相关性并未克服冗余的缺陷,不能满足高精度识别的需求[12]。

在实际使用过程中也需注意SVM会出现局部极小值结果,多是通过网格搜索(GSA)确定最优SVM[13],采用上述方法进行数据搜索时需依次确定网格所有样本点结果,随着参数的增加,计算量也会发生指数级迅速上升的情况,从而造成分类的精度与计算效率下降结果[14]。结合上述分析结果,

本文对时频域进行特征降维处理时通过主成分分析(PCA)的方式实现高维信号噪声。为了抑制SVM算法分类精度低的问题,引入PSO算法进行加强,并使SVM算法获得更优的核函数。

1 实验方案

本实验按照图1中的齿轮箱系统开展测试。本次在系统中加入伺服电机为齿轮箱的主被动齿轮提供驱动力,再利用制动器对齿轮箱进行制动控制。针对扭矩传感器和加速度传感器设置以下参数:控制灵敏度等于20 mv,最大量程为450 m/s2,同时设定频率范围在0.5 Hz～10 000 Hz之间,保持谐振频率为25 kHz的固定值,根据以上条件确定齿轮箱的负载及其振动状态,数据采样的频率为5 000 Hz,持续采样时间控制在0.5 h。

▲图1 实验装置

动齿轮和被动齿轮的参数见表1所示。主动齿轮内含有特定长度的裂纹,可通过表达式Li=i×(R-r)/4计算得到,i可以取值为0、1、2、3,R、r分别为主动齿轮齿根圆半径和主轴半径[15]。

表1 主动齿轮和被动齿轮的参数

表2给出了主动轴的转速与载荷选取结果。将主动轴转速和载荷间隔取五个数值,总共形成了25种齿轮裂纹故障,可通过正交测试的方式从中确定100组参数,并把每个样本分成20段,由此形成2 000个分段。

表2 主动轴的转速与载荷

2 特征信号提取方法

在主动齿轮中加入1/4裂纹缺陷,主动轴转速1 200 r/min,同时在齿轮箱中施加8 N·m的振动载荷,实际形成的振动波形见图2。

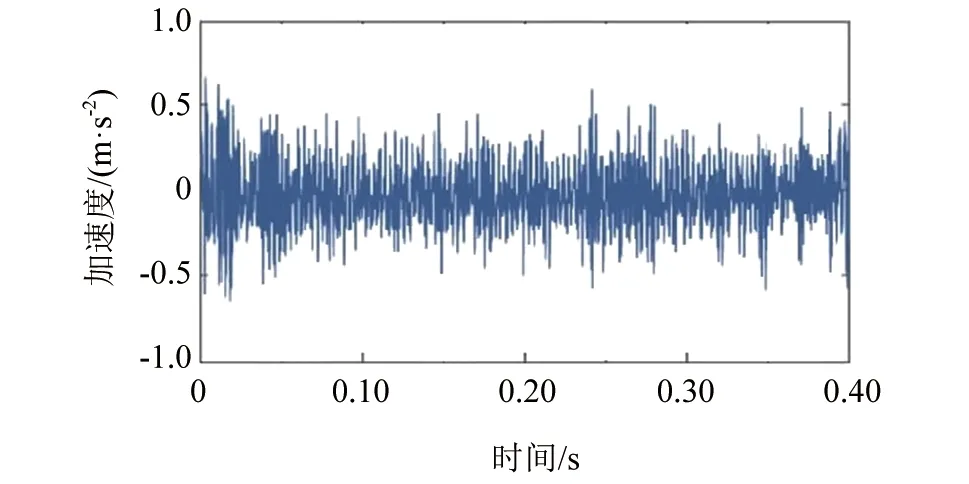
▲图2 齿轮箱振动信号波形

图2给出了振动信号FFT转换形成的幅值谱图。从图2中可以卡到在齿轮箱内存在复杂的振动频率,依次对应主动齿轮、被动齿轮的啮合频率与2～5倍频率。当齿轮箱的振动幅值谱被确定后,再利用表4数据计算得到频域特征。

测试上述2 000组振动信号的时频域,从中提取出时域、频域特征共10个,通过组合得到2 000行、20列大小的矩阵T,以下为矩阵表达式[16]。

(1)

式中:tji为第j组参数特征i,取值范围包括1,2,3,…,p,j的取值范围是1,2,3,…,q,p=20,q=2 000。

之后将特征矩阵T转换成式(2)的向量形式。

T=⎣t1t2t3…tp」

(2)

根据式(3)计算列向量均值。

(3)

利用式(4)计算样本协方差。

(4)

分解协方差矩阵Cov(T)的特征值得到特征矩阵U和特征参数λ,构成信号主成分的部分为d阶初始向量。

以PCA方法处理齿轮箱的振动数据得到表3所示的特征能量。计算结果表明,PCA初始4阶特征的能量比等于82%,初始5阶的特征能量比则增加到了92%,6阶特征能量比也发生小幅提高,为94%,结合以上特征能量比数据和处理效率,选择初始5阶特征构成PCA的特征集合。

表3 前6阶特征能量比

3 结果分析

利用样本最大边距超平面设置训练分类指标,形成式(5)所示结果。

w·x+c=0

(5)

假设粒子全局最优解为Pg,将粒子i的速度表示成Vi,将粒子的速度和位置结果表示为式(6)～(7)。

(6)

(7)

式中:c1和c2都是加速度系数;w表示粒子群经过搜索得到的惯性因子;r1和r2是[0,1]区间中的参数;αi代表粒子i的最优位置。

根据齿轮裂纹特征设置分类精度,同时采用PSO调节SVM核函数[17-18],结果见图3。

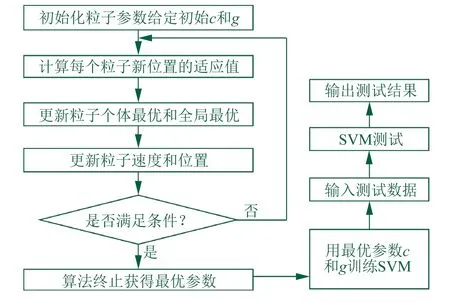
▲图3 SVM-PSO的流程图

将γ、d的初值依次控制在0.6和1.5。将粒子群例子数控制在100,同时根据表4确定PSO参数。

表4 PSO的参数设置

将γ、d的初值依次控制在0.6和1.5。将粒子群例子数控制在100,同时根据表4确定PSO参数。

将计算所得结果与GSA比较。选择400组初始齿轮故障数据作为训练集,之后测试剩下的400组样本,得到图4结果。

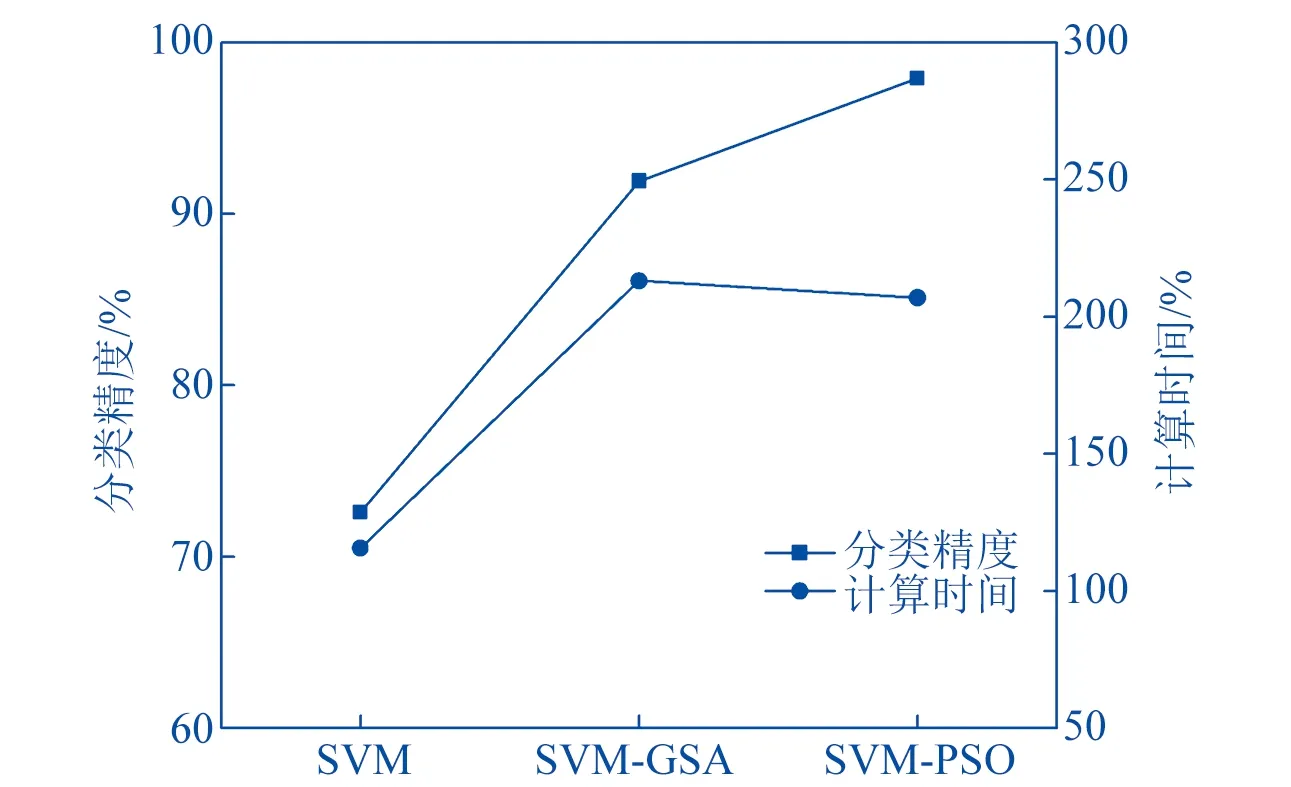
▲图4 SVM-PSO分类精度和计算时间结果

对比图4结果可以发现,以SVM-PSO算法进行处理时相对其它算法表现出了更高的精度,算法时间介于SVM和SVM-GSA之间,能够满足优异的分析性能,根据上述结果可以判断PSO算法对SVM核函数优化后能够能够实现分类精度的显著提升,而且经过算法优化后,还会明显增加整体计算量,这就要求在后期阶段继续调节计算效率。

本文在验证算法的分类效果时,通过实验模型和其它模型进行对比的方式得到图5所示结果。

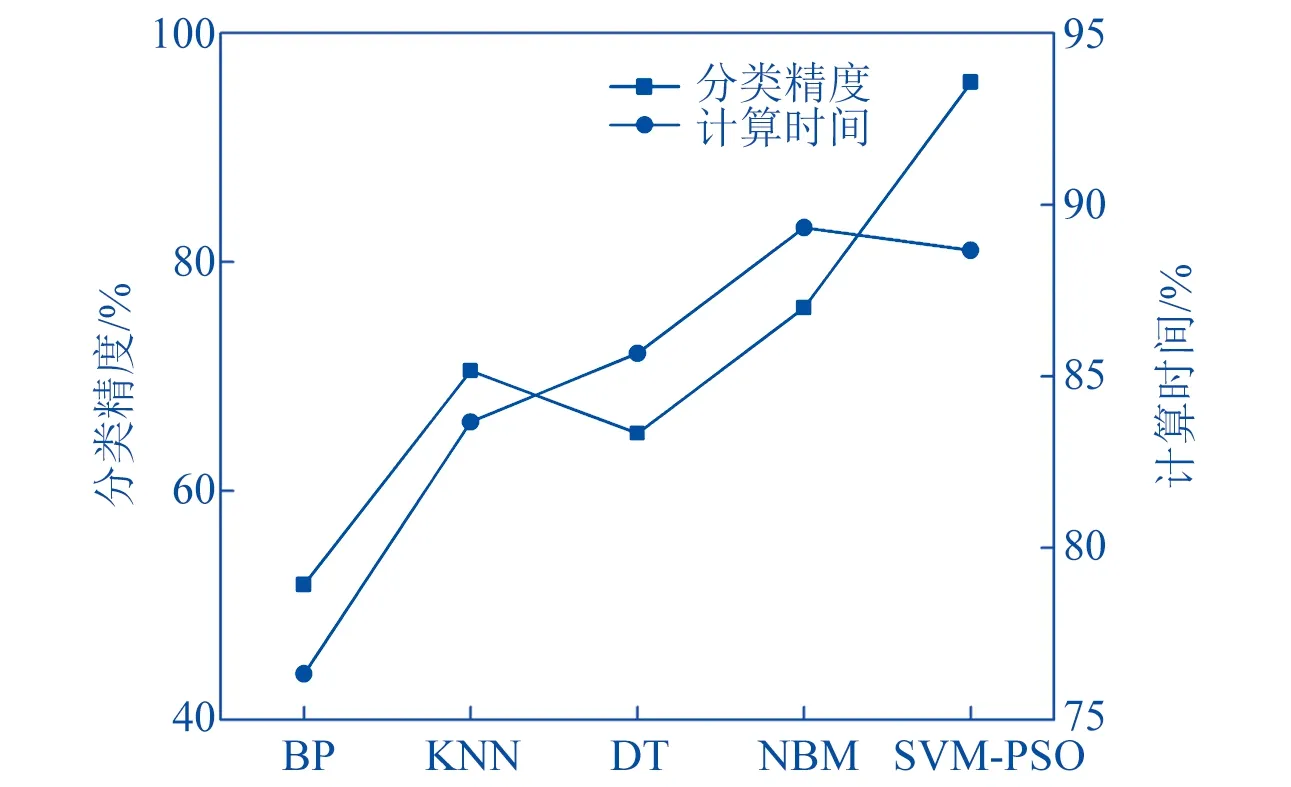
▲图5 不同分类算法下分类结果

对图5结果进行分析可以发现,以SVM-PSO算法进行处理时的精度最高,能够满足高稳定性要求,所需计算时间也较合适,表明PSO方法有助于算法分类精度及效率都获得显著提升。SVM-GSA按照网格区分的形式来完成全局搜索,可以通过增加网格数的方法来提升计算精度,但会导致计算时间的延长。

开展机器学习的时候,将样本数设置在不同数值的条件下时,训练分类性能也存在较大偏差,因此需对比不同样本数的测试结果,得到图6结果。

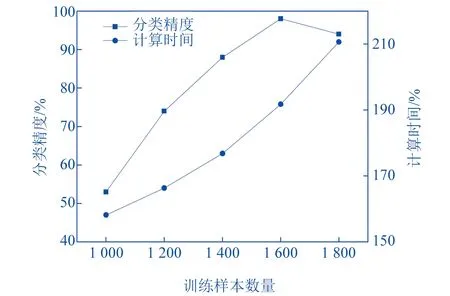
▲图6 不同训练样本数下分类结果

图6显示,设置不同样本数时所需的处理时间也具有较大差异,由此达到更高的分类精度,而当训练样本数太多时则会出现过拟合的状态,考虑到实际测试的样本数较少,容易引起分类不稳定结果。综合判定训练样本数设置1 600是相对比较合理的。

为了测试不同齿轮裂纹长度下的时频域特征差异性,分别选择10个时域与频域特征参数开展计算,并跟前期结果进行对比,如图7所示。

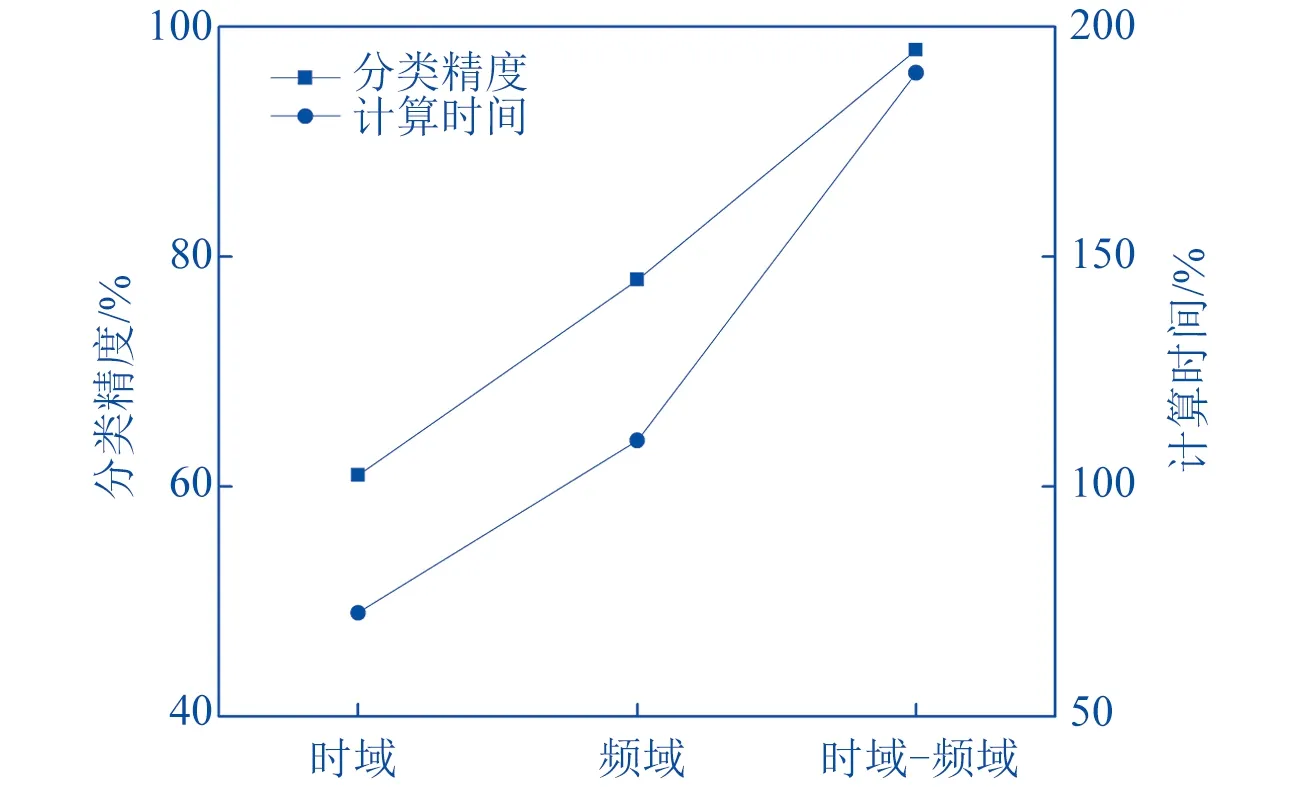
▲图7 不同时-频域特征下分类结果

图7显示,只计算时域特征时可短处理时间,但会导致分类精度下降,此外频域特征相对时域特征可以达到更高的精度,可以根据以上结果判断齿轮裂纹长度引起的频域特征变化更明显,可利用频域特征作为判断指标。

4 结论

(1) 以SVM-PSO算法进行处理时相对其它算法表现出了更高的精度,能够满足优异的分析性能。

(2) 以SVM-PSO算法进行处理时的精度最高,能够满足高稳定性要求,所需计算时间也较合适,PSO方法有助于算法分类精度及效率都获得显著提升。

(3) 样本数对处理时间影响很大,综合判定训练样本数设置1 600是相对比较合理的。

(4)采用时域特征时会导致分类精度下降,外频域特征相对时域特征可以达到更高的精度。