基于2R型并联舰载稳定平台的运动学及静力学

董 睿, 鸦 婧, 俞竹青

(常州大学 机械与轨道交通学院,江苏 常州 213100,E-mail:dong1996r@163.com)

随着机构理论的深入发展,并联机构也渐渐成为机械应用的主体[1]。并联机构一般为:上平台用2个或者2个以上的分支相连,机构具有2个或2个以上的自由度,并通过多驱动机构并联驱动来控制机构的末端达到想达到的位姿。但从另一角度出发,只要是多自由度的,驱动器分配在不同的环路上的并联多环机构都可以称之为并联机构。

与串联机构相比,并联机构有如下优点:首先并联机构有多跟杆支撑,结构稳定;第二,刚度大,承载能力大;第三,关节活动误差不会积累和放大,误差小,精度高;第四,驱动模块任意放在机构末端,系统惯性小[2]。

目前并联机构已经吸引了国内外学者的广泛关注,其在稳定平台中已经得到了广泛发应用。赵万卓等[3]提出了一种3-RPS并联稳定平台,主要解决越野救护车和医疗运输过程中所受到的外界环境干扰问题。浙江大学郑祥谱[4]基于Stewart并联机构提出了可应用于普通光学相机上的稳定平台,可以抵消拍照时手抖动对相片质量的干扰问题。罗二娟[5]提出了基于3-RPD机构的车载稳定平台,用于抵消运输过程中路面颠簸对精密仪器设备等损坏。

本文在之前的研究基础上提出一种新型并联稳定平台,主要应用于舰载方面。其能实现两自由度的转动,主要抵消海浪对舰身的横摇和俯仰的扰动,这里称之为2R(两转动自由度)型并联稳定平台。此2R型并联机构在只需要两自由度的转动的应用场景里面,相比较与前面提出的Stewart并联机构等,结构上更紧凑可靠,成本上更经济,控制精度上更精确。

本文我们将对此种基于2R型并联机构的稳定平台进行分析。先对2R并联机构结构进行描述,并运用Kutzbach Gruble公式进行自由度校验。紧接着对此2R型并联机构进行位姿反解,求运动平台位姿与驱动器的对应关系;再结合Matlab进行静力学求解,求得各杆件在各位姿点受力大小图以及各构件在设定载重下最大受力值;接下来结合算法在Matlab上进行仿真,求得位置逆解时各驱动器伸缩长度与对应位姿的映射关系。

1 2R型并联机构构型

▲图1 2R型并联机构示意图

2R并联机构简如图1如示,包括一个动平台(上)ΔABC,静平台(下)ΔDEF,一条RPS型驱动支链 ,一条SPS型驱动支链和一个固定杆构成(R,P,S分别代表转动副,移动副和球面副)。其中杆L1为固定杆,方向垂直向上,下端与静平台固定连接,上端由球绞和动平台铰接。RPS支链为,杆L2通过球绞与动平台连接,通过移动副与杆L3链接,杆L3再通过转动副与静平台连接;SPS支链为,杆L4通过球绞分别与动平台铰接,通过移动副与杆L5连接,杆L5再通过球绞与静平台连接。

设计此2R型并联稳定平台,通过两个移动副驱动杆L2,L4的移动来达到控制动平台绕X,Y轴旋转的角度,以实现动平台的水平稳定。

下面对其进行自由度分析

改机构共有两个自由度,分别为绕X,轴和Y轴的旋转。采用黄真修正的Kutzbach Gruble公式[6],验算机构自由度,即

(1)

式中:M表示机构的自由度;n为包括机架在内的构件数目;g表示运动副数目;机构无公共约束,因此机构的阶数d=6;fi代表第i个运动副的自由度数;机构无并联冗余约束和局部自由度,故ν=0,ζ=0。

这验算结果与设计的自由度完全相同,所以自由度可靠。

2 并联机构位置逆解分析

▲图2 机构坐标系图

为方便平台的位姿求解,在机构中建立坐标系。在静平台中建立静坐标系,以静平台上D点为坐标原点O,按右手法则以此建立静坐标系O-XYZ,记作静坐标系{O};在动平台中建立动坐标系以动平台上A点为坐标原点O′,按右手法则以此建立动坐标系O′-X′Y′Z′,记作动坐标系{O’},如图2所示。

当机构的动平台保持水平时,以坐标的方式展现构件之间的尺寸关系。机构上各点在静坐标系{O}中的坐标位置如下:A=(0,0,h);B=(a,0,h);C=(a/2,b,h) ;D=(0,0,0);E=(a,0,0);F=(a/2,b,0)。

动平台上各点在动坐标系{O′}中的位置为:A′ =(0,0,0);B′=(a,0,0);C′=(a/2,b,0) 。

与串连机构不同的是,在并联机构的位置分析中,位姿反解比较简单。这里可以用反解的方法解开并联机构,通过给定位置和姿态来求解杆L2,L3的伸缩量。在得知位姿与杆长之间的对应关系,我们便可以反过来,通过控制驱动杆的杆长来控制动平台的位姿。

对并联机构的逆解方法,是将动坐标系中任一点的位置通过坐标变换方法变换到静坐标系中的位置,便可解出驱动杆的伸缩量[7]。

目前对坐标空间变换的描述的主要方法有:欧拉角法,方向余弦矩阵法和四元数法。这里用到欧拉角法:任何空间坐标的旋转可以分解为绕三个互相垂直轴的三次连续旋转组成的序列。值得注意的是:三次旋转轴组合的次序不同,会导致结果不同。这里采用常用的顺序,即先绕Z轴旋转,再绕Y,X轴旋转的顺序。所以,任何一个旋转都可以表示为,依次绕Z,Y,X轴三个相互垂直的旋转轴旋转的三个角度的组合,这三个角度成为欧拉角。

设平台绕Z轴旋转角度为ψ,绕Y轴旋转的角度为θ,绕X轴旋转的角度为φ。

根据欧拉角求旋转矩:

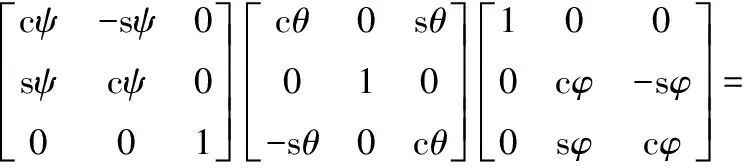
(2)

式中:c: cos;s: sin。

将欧拉角中绕Y轴旋转的称为偏航角,绕X轴旋转的角成为俯仰角,绕Z轴旋转的角成为翻滚角。

因为此并联机构稳定平台只有偏航角和俯仰角两自由度的旋转,不存在Z轴翻滚角的自由度。所以令翻滚角φ=0,带入上述公式中。

此时旋转矩阵变化为

Rot(0,θ,φ)=Rot(y,θ)Rot(x,φ)=

(3)

该机构无论上平台发生什么运动,该平台的动坐标原点A在静坐标的位置并没有改变。可以通过如下公式计算出,当动平台发生任一位置变化是,其上任意一点在静坐标系中的坐标位置[8]。

p′=R*p+T

(4)

式中:R为旋转矩阵;p为平台上某点在动坐标系中的坐标位置,p′为该点静坐标系中的坐标位置;T为动坐标系原点在静坐标系中的位置,这里即为A点在静坐标系中的坐标

将参数带入式中即表示为

(5)

式中:B′,C′∈R3×1

动平台上B,C点发生了绕X,Y轴转动后而成的点B′,C′,其在静坐标系中的位置如上。当B′,C′点的坐标知道且E,F点坐标不动,则分别对B′E,C′F取求模,便得出杆的总长量。

(6)

此刻移动副所产生的驱动长度记作Y1,Y2,则当需要X轴,Y轴分别产生φ,θ角度的旋转来抵消外界的干扰时,移动副所需驱动的长度分别表示为:

(7)

3 并联机构静力分析

机构为一确定结构,其受力情况分析如下。

设计中,拟定上平台所能承载的垂直载荷记为G。当平面倾覆时,测得X,Y轴倾角分别为α,β。

驱动支链RPS上端是球绞连接,下端是转动副连接,忽略杆转动时关节所受的摩檫力,则两端对此驱动支链各施加一个力,所以支链RPS是二力杆,受力方向沿杆的方向。

在之前的位置逆解工作中,支链的首端B′末端E在静坐标中的位置坐标已知。通过对支链的方向向量单位化,便得出驱动支链RPS的方向向量,记作θ2,则:

(8)

驱动支链SPS上下两端皆是球绞连接,忽略杆转动时关节所受的摩檫力,则两端连接处对此支链仅施加一个外力,所以支链SPS也是二力杆,受力方向沿杆的方向[9-10]。

▲图3 固定杆受力图

同样,可以求出驱动支链SPS的单位方向向量记作θ3,则:

(9)

固定杆上端是球绞连接,下端是固定端约束。受力分析如图3所示,其上端受一个大小,方向皆未知的力,下端固定端受来三个方向的转矩和力。

综上所诉,B,C点处受力是一个大小未知的力,记作F2,F3。F2,F3的矢量方向是沿杆方向,将其沿X,Y,Z轴方向分解,得到的其在X,Y,Z各方向分力记作:F2x,F2y,F2z,F3x,F3y,F3z

(10)

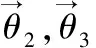
▲图4 动平台A点受力示意图

A点处受力是大小和方向皆未知的力,将其沿X,Y,Z轴方向分解为方向已定,大小待定的分力。如图4所示,分别记作:F1x,F1y,F1z。

动平台在任意姿态的总体受力图如图5所示。

动平台上各点尺寸关系如图6所示。

▲图5 动平台受力示意图

▲图6 动平台尺寸示意图

根据空间任意力系平衡方程知,当动平台处于静力学平衡时满足如下平衡方程:

(11)

在动平台的A点建立静平衡方程,将上述变量带入带入公式中,列出如下六个平衡方程:

(12)

将平衡方程以如下矩阵形式表达:

(13)

式中:H(α,β)∈R6×5

整理得H(α,β)式如下

(14)

分析知矩阵秩r[H(α,β)]恒为5.未知力是F1x,F1y,F1z,F2,F3,故恒有解。

方程解得。

(15)

整理得每杆受力关于角度α,β的方程

(16)

结合上文,对上式的计算结果的意义进行分析知,RPS支链的受力为二力杆件,上式计算出的力F2即为该支链受到的压力。同理SPS支链也是二力杆,上式中计算出的力F3即为该支链所受到的压力。固定杆上端分解出的力F1Z也是固定杆受到的压力。进一步对其进行分析得出内应力,便于我们对材料 的强度进行校核。

4 基于Matlab的仿真验证

机构各支链最大受力点以及位姿与受力大小的映射关系能够帮助我们更合理的设计与使用该并联结构稳定平台。因此计算各支链的位姿与受力映射是分析研究机构的重要环节。目前对机构受力求解的主要方法有数值分析法(极限搜索法),有限元分析法等。本文中在Matlab平台通过搜索算法研究各支链最大受力值。

前面的结构尺寸参数,现拟定如下,a=60 cm,b=40 cm,h=40 cm,G=5 000 N。结合稳定平台的在舰载使用工况下工作要求,拟定横滚角,即绕X轴的旋转角α∈(-10°,10°),,俯仰角,即绕Y轴的旋转角β∈(-20°,20°)。结合算法在Matlab平台仿真。获得的平台位姿与受力关系如图7所示[11]。

▲图7 各支链受力与位姿关系图

在α∈(-10°,10°),β∈(-20°,20°)范围内,求出两支链和固定杆所受正压力以及固定杆所受的弯曲力的最大值及此时动平台对应的位姿,记录于如下表1所示[12]。

表1 活动范围内各杆件最大受力/N

基于前面的结构参数,结合数值分析算法在Matlab平台计算出两移动副的驱动伸缩量与动平台的位姿关系如图8所示。

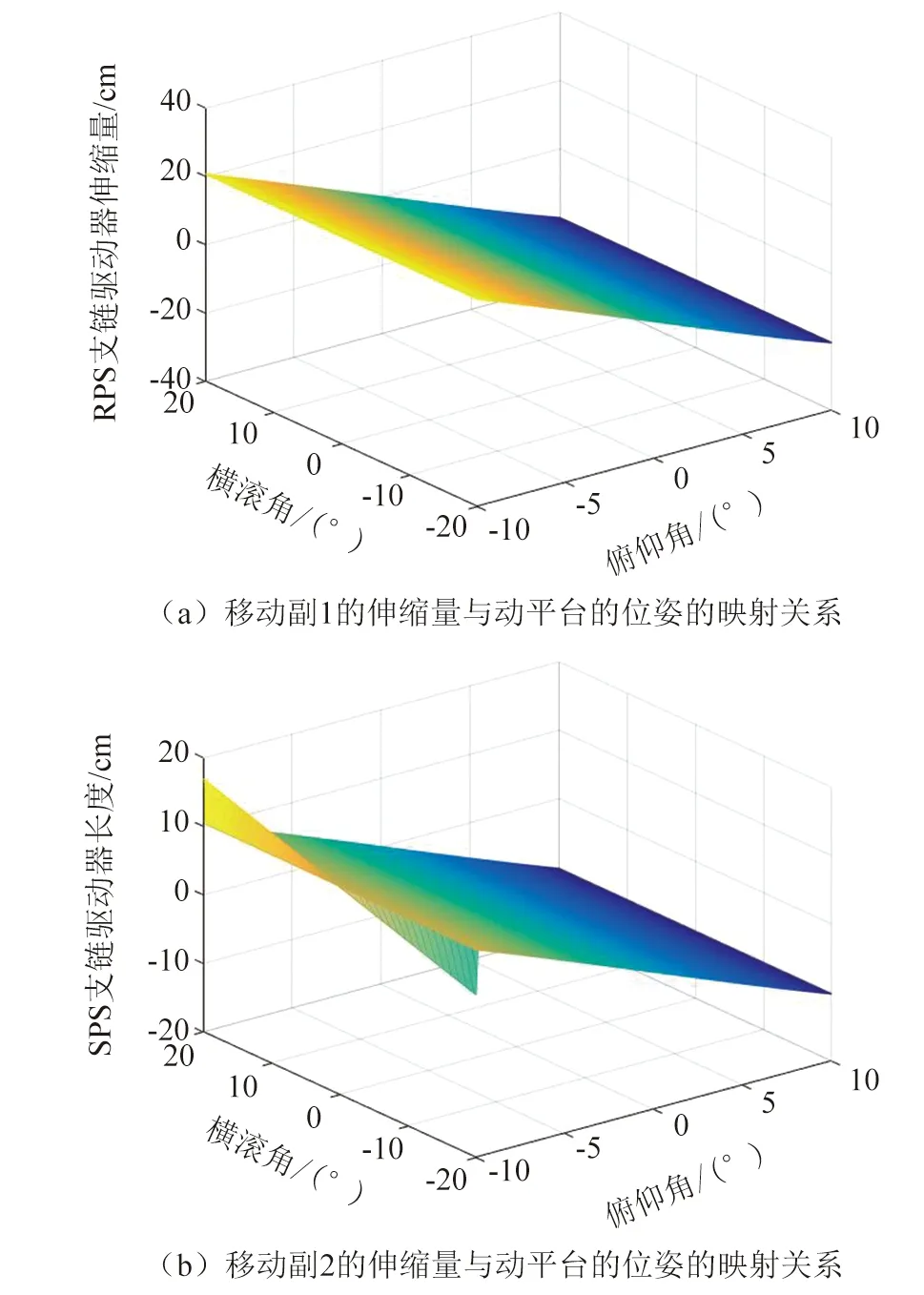
▲图8 移动副位移与位姿关系

当我们需要计算某角度位姿的杆伸长量与各杆受力时,也同样可以在该matlab仿真中获得。例如,当动平台在静坐标系中的角度姿态为ψ,θ,φ为{0,15.6°,-6.8°},经matlab计算移动副的伸缩量为13.19(负数表示收缩,正数表示伸长);移动副的伸缩量为-3.5。固定杆所受的正压力为1.058 kN;固定杆所受弯曲力为0.329 24 N; SPS支链所受压力为2.059 kN;RPS支链所受压力为0.806 2 kN。

5 总结

(1) 提出一种新型基于2-R并联机构的舰载稳定平台,机构由动平台,定平台,固定杆RPS支链和SPS支链构成。可以实现两自由度的旋转以抵消海浪对舰身的横摇和俯仰的扰动。

(2) 通过对驱动支链与动平台位姿关系的分析给出机构位置逆解的解析式。并在Matlab平台仿真得驱动器伸缩量与动平台的位姿关系图。

(3) 通过建立静力学平衡公式求得各杆件受力大小与位姿的解析表达式。建立算法通过Matlab平台仿真,求得各杆和支链所受弯曲力以及正压力与位姿的关系图。并通过搜索算法找出各组受力中最大值,以便后期校核杆件的强度。