线驱动多关节巡检机械臂运动轨迹

2023-07-25王浩宇岳海涛杨国华

机械设计与研究 2023年2期

王浩宇, 路铠, 王闯, 岳海涛*,, 4, 杨国华

(1.中煤科工开采研究院有限公司,北京 100013,E-mail:782562857@qq.com; 2.辽宁工程技术大学机械工程学院,辽宁阜新 123000; 3.内蒙古霍林河露天煤业股份有限公司,内蒙古霍林郭勒 029200;4.辽宁省大型工矿装备重点实验室,辽宁阜新 123000)

受充填工艺和充填体脱水固结影响,充填体和顶板间产生缝隙空间,导致充填体存在不接顶现象,严重影响充填效果。由于充填区域封闭或仅有极狭小的空间,传统井下设备无法有效的检测不接顶区域空间并计算接顶率,往往采用人工巡检及经验判断的方式对充填接顶率进行检测,人工巡检劳动强度与安全隐患较大[1-3]。巡检机器人的出现,正逐步实现人工巡检的替代,是实现井下作业及运维管理的有效技术手段之一[4-5]。然而现有巡检机器人往往无法穿过障碍物监测设备、复杂空间内部状况[6],在井下复杂环境无法灵活越障[7],对非结构化复杂空间的巡视灵活性、检测可达性效果较弱[8]。研究一种可进入井下复杂空间且检测可达性优秀的灵活机械系统,对于进行井下狭窄复杂的非结构化不接顶充填空间信息数据采集、充填率测量计算和充填效果评价具有重要意义。

连续型机器人也称为蛇形机器人,具有自由度多、弯曲特性好的特点[9],为井下非结构化复杂空间实现灵活巡检提供了一种选择。目前国内外学者对蛇形机器人开展了诸多研究。Walker等[10]研制了一系列气压驱动的仿象鼻连续型机器人样机,可实现弯曲和伸缩运动。Nabil Simaan[11]研发了一种可用于咽喉等外科手术的医疗连续型机器人,并成功应用于微创手术。Chen和Pham等[12]研究一种应用于结肠镜检查中内窥镜末端的单段连续型弯曲机构,可配合人体肠道内壁作用力和机器人自身控制完成内窥镜介入。徐文福等[13]研发了一款应用于核电站等狭小空间作业的绳索驱动冗余机器人,其具有18个自由度,运动灵活。高庆吉、牛国臣等[14]研究了一种线驱动的柔性连续型机器人,用于飞机油箱检查,安全性高,灵活性好。姚艳彬[15]设计了一款用于飞机装配的蛇形机器人,具有10个自由度,在视觉系统辅助下具有一定的避障能力。然而目前蛇形机器人特点为精细化,操作臂短小灵活且多为弹性结构,工作空间不大且承载能力较弱,不适用于矿山开采领域。

本文给出了一种充填不接顶非结构化空间多关节线驱动巡检机械臂,以期提升非结构化充填不接顶狭域空间不接顶率的自动化检测。建立了线驱动巡检机械臂的运动学模型,分析了各关节驱动空间、关节空间及工作空间三者间的映射关系,对线驱动巡检机械臂工作空间进行了仿真分析,针对多关节间的耦合影响进行了解耦分析,对建立的运动学映射关系及解耦方程进行了仿真验证,以充填不接顶非结构化空间的可达性巡检测试为应用背景,开展了线驱动巡检机械臂运动轨迹验证性试验。

1 机械臂整体结构

为提升充填不接顶间隙的巡检灵活性和检测可达性,本文提出的线驱动巡检臂由多个关节串联而成,巡检机械臂结构如图1所示。关节由布线圆盘、杆臂、球型头及凹槽结构组成,关节模型如图2所示,布线圆盘主要对驱动线起导向固定作用;为了减小机械臂重量,提高负载能力及运动响应速度,关节杆臂设计为中空结构;末端关节可装夹激光雷达等其他空间检测传感监测组件,实现对充填不接顶非结构化空间的检测;球型头部及凹槽构成球型铰链,使连接关节具有俯仰和偏航两个自由度。线驱动巡检机械臂为模块化设计,可根据不同工作环境选用不同型号的关节。每个关节由三根间隔120°的驱动线控制,关节数为n,驱动线数为3n,末端关节驱动线穿过前端所有关节。每组驱动线分别带动相应关节进行两自由度弯曲运动,各关节串联使巡检机器人实现三维空间中的俯仰、偏航运动。

▲图1 巡检机械臂整体结构

▲图2 关节模型

2 线驱动巡检机械臂运动学分析

巡检机械臂采用线驱动形式,可使质量较大的驱动器远离末端执行器,从而减轻末端执行器惯量,提高动态性能,且几何空间占用少。为保证线驱动巡检机械臂的运动灵活性,机械臂各关节串联,各驱动线并联,为耦合串-并联[16-17]结构。对线驱动巡检机械臂驱动空间、关节空间、操作空间三者的运动映射关系开展运动学分析[18-19]。

运动学算法解析基于以下前提条件:

(1) 将球铰连接处、驱动线与布线圆盘接触处视为光滑,忽略摩擦力的影响。

(2) 忽略线驱动巡检机械臂驱动及运动部件间相互作用力的影响。

(3) 各关节形状、尺寸均相等,忽略制造误差的影响。

2.1 关节空间与操作空间的运动映射关系

线驱动巡检机械臂关节空间是指机械臂各关节运动空间。关节空间至操作空间的运动映射关系可在建立D-H坐标系后,用基座坐标系至末端坐标系的齐次变换矩阵T表示。建立各关节D-H坐标系如图3所示。

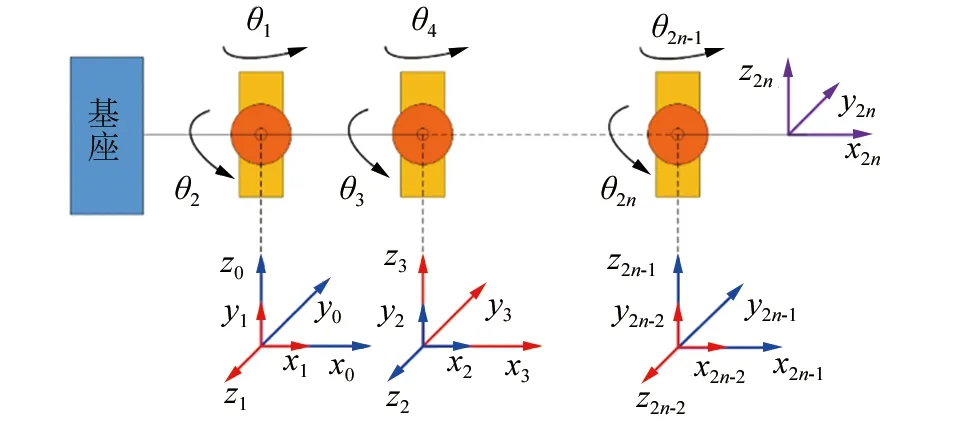
▲图3 D-H坐标系

(1)

根据各关节齐次变换关系,将齐次变换矩阵顺序相乘,解算出末端执行器位姿在基座坐标系中的表达,线驱动巡检机械臂正运动学方程为:

(2)

2.2 驱动空间与关节空间的运动映射关系

线驱动巡检机械臂驱动空间为驱动线位移空间,为提高线驱动巡检机械臂负载能力,便于搭载各种传感器完成检测任务,各关节采用球铰连接方式,每个关节由三根驱动线并联控制,关节驱动线间存在耦合关系,为保证井巷巡检工作的正常进行,需对其进行解耦分析。

线驱动巡检机械臂运动过程中,通过改变驱动线长度控制关节转动角度。线驱动巡检机械臂单关节系统中有3个线驱动输入和2个运动自由度输出,单关节驱动空间与关节空间的运动映射关系分析即解算3根驱动线的长度变化量Δlk(1≤k≤3)与2个自由度变量α、β间的定量关系。

▲图4 单关节简化模型

建立单关节简化模型如图4所示。面A1A2A3和面B1B2B3分别代表相邻关节的布线圆盘面,线段A1B1、A2B2、A3B3分别代表关节相对应的三根驱动线l1、l2、l3,点P为关节转动中心,O1、O2分别为面A1A2A3和面B1B2B3的中心。以O1、O2为原点,关节杆轴向为z轴,自由度转动轴方向分别为x轴、y轴,建立空间直角坐标系O1x1y1z1、O2x2y2z2。以P为原点,建立基准坐标系O0x0y0z0。

坐标系O1x1y1z1绕其x轴转动α角,再沿其原z轴方向平移h距离后得到坐标系O0x0y0z0。则坐标系O1x1y1z1到坐标系O0x0y0z0的齐次变换矩阵为:

(3)

坐标系O0x0y0z0绕其y轴转动β角,再沿其转动后的z轴方向平移-d距离后得到坐标系O2x2y2z2,则坐标系O0x0y0z0到坐标系O2x2y2z2的齐次变换矩阵为:

(4)

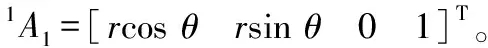
(5)

则关节的驱动线A1B1长度为:

(6)

同理可得驱动线A2B2、A3B3的长度。

驱动线长度变化公式为:

Δlk=|AkBk|-(h-d)k=1,2,3

(7)

根据上述公式,可解算出单关节3根驱动线长度变化量与自由度变量α、β之间的定量关系,根据实际需求进行正逆运动学分析,为线驱动巡检机械臂多关节耦合运动建立理论基础。

2.3 线驱动巡检机械臂工作空间分析

对关节变量随机取样,取关节最大转角为20°,两自由度变量满足下式:

α2+β2≤(20°)2

(8)

▲图5 单关节工作空间

设计关节连杆长度为85 mm,在关节变量取值范围内随机取6 000组采样点。运用蒙特卡洛法绘制单关节工作空间如图5所示。可见,单关节工作空间为圆盘面包络状,关节末端参考点的运动范围能够覆盖三维空间中一定范围内任意方向。

线驱动巡检机械臂由多关节串联,蒙特卡洛法基于随机抽样,采样点集中于工作空间中心,边界描绘不清晰,改进算法如下:

(9)

式中:i=1,…,u,u为关节数;p=1,…,q,q为细分数,采样数s=qu;α,β为关节自由度变量。

如图6所示,多关节工作空间为中间薄,四周厚的空心半球状包络空间。因线驱动结构,巡检机械臂末端执行器体积小、惯量轻,因此在三维空间中具备较大工作范围,可满足狭窄复杂空间内进行检测的工作需求。

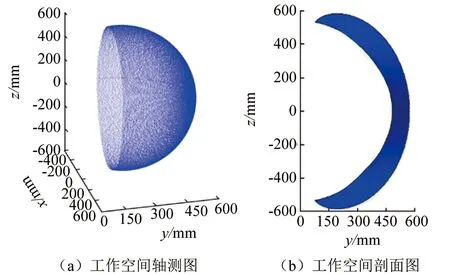
▲图6 多关节工作空间

3 驱动空间与关节空间运动学分析

▲图7 两关节驱动线配置

线驱动巡检机械臂由多关节串联而成,自由度多,运动灵活性好,可保证巡检机械臂能实现多角度监测。因末端关节驱动线穿过前端所有关节,前端关节运动会带动后端关节同步运动而产生耦合影响[20],需进行解耦分析。将所有关节从基座处开始编号,图7为机械臂末端关节示意图。关节n的驱动线穿过关节n-1的布线圆盘,关节n-1运动时,关节n的驱动线需同步变化。因此分析线驱动巡检机械臂的驱动空间与关节空间运动关系时应考虑各关节间的耦合影响,进行解耦分析。

3.1 相邻关节运动学分析

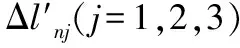
(10)

式中:f(α,β,θ)代表驱动线长度计算公式:

(11)

(12)

解耦分析得关节n驱动线长度变化量Δlnj(j=1,2,3)为:

(13)

通过上述解耦方程,可通过两关节自由度变量求解各自驱动线长度变化量,为多关节驱动空间与关节空间运动学解耦分析奠定理论基础。

3.2 多关节运动学分析

设关节i(1≤i≤n)的2个自由度变量为αi、βi,首根驱动线在布线圆盘的位置标识为θi,解耦分析后驱动线长度变化量为Δlij(j=1,2,3),由上文类比推理得:

(14)

通过上述解耦方程,可求解各关节驱动线长度变化量,实现各关节自由度变量独立控制,从而实现对线驱动巡检机械臂灵活控制,完成不接顶充填非结构化复杂空间内多角度灵活巡检作业。

4 线驱动巡检机械臂运动仿真

为验证线驱动巡检机械臂狭窄复杂空间内的运动灵活性,保证巡检机械臂对充填不接顶非结构化空间的检测能力,对线驱动巡检机械臂运动进行仿真分析。

对单关节运动进行仿真分析,关节长度L=85 mm,由三根驱动线控制,驱动线孔位分度圆直径r=34 mm。初始状态时,线驱动巡检机械臂末端坐标为[85,0,0],布线圆盘间距离d=30 mm。关节俯仰角在[-20°,20°]内正弦变化,偏航角在[-20°,20°]内余弦变化,周期为2π,令采样次数s=50,角度变化曲线如图8(a)所示,运用MATLAB进行仿真分析,得到驱动线长度变化曲线如图8(b)所示,对末端运动轨迹和末端位置坐标进行仿真分析,分别得到如图8(c)所示曲线。可知,单关节2个自由度变化时,驱动线长度可及时改变,控制线驱动巡检机械臂运动,其末端轨迹为规则图形。

对两关节运动进行仿真分析,线驱动巡检机械臂总长F=170 mm,分为两节。每节长度L=85 mm,由三根驱动线控制,驱动线孔位分度圆直径r=34 mm。因线驱动巡检机械臂结构的特殊性,关节间存在运动耦合关系。关节1运动时,为消除关节1对相邻关节2的运动耦合影响,关节2的驱动线长度需同时改变。

单关节有约束时,两关节角度变化曲线如图9(a)所示,对关节2运动解耦分析,得到两关节各驱动线长度变化曲线如图9(b)所示,关节2末端运动轨迹如图9(c)所示。

线驱动巡检机械臂两关节联合运动时,关节2的运动为自身运动叠加关节1的解耦合运动。线驱动巡检机械臂末端坐标为[170,0,0],当两关节俯仰角在[-20°,20°]内正弦变化,偏航角在[-20°,20°]内余弦变化,变化周期为2π,令采样次数s=50,两关节角度变化曲线如图10(a)所示,运用MATLAB进行仿真分析,得到各驱动线长度变化曲线如图10(b)所示,对末端运动轨迹进行仿真分析,得到如图10(c)所示曲线。由图可见,两关节各自由度变化时,关节2驱动线叠加关节1的耦合影响,控制线驱动巡检机械臂运动,其末端轨迹为规则图形,验证了多关节解耦分析的正确性。

▲图8 单关节运动分析

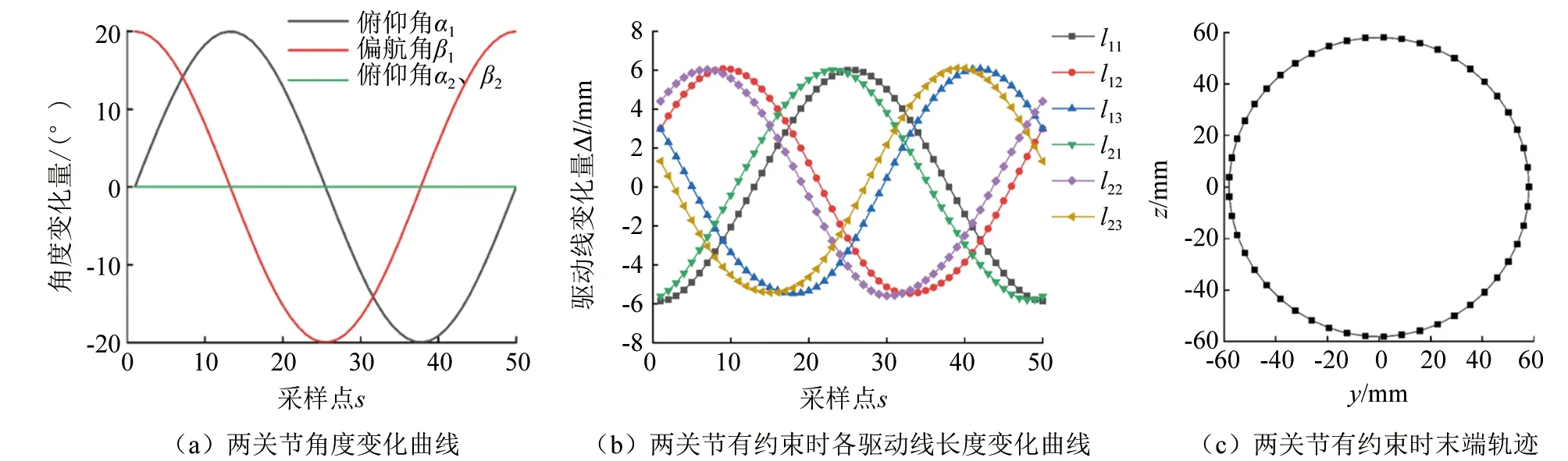
▲图9 两关节有约束运动分析

▲图10 两关节联动运动分析

5 线驱动巡检机械臂避障性能测试

5.1 线驱动巡检样机

为验证线驱动巡检机械臂对狭窄复杂空间的避障巡检灵活性,搭建了如图11所示的线驱动巡检机械臂原理样机,共由7个关节串联,每关节由3根驱动线并联控制。为提高机械臂控制便捷性,设计姿态控制模块,可远程快速进行机械臂位姿调整,集成上位机可对传感器采集信息进行实时显示,满足巡检需求。

▲图11 线驱动巡检机械臂原理样机

5.2 弯曲运动测试

为测试线驱动巡检机械臂原理样机平面弯曲运动能力,根据本文所构建运动解耦方程,利用基于PLC的多电机控制系统进行原理样机平面弯曲运动性能试验。保证各关节旋转角度一致,仅改变各关节自由度变量α,使机械臂在同一平面内弯曲运动。图12(a)中各关节偏角α=7°,β=0°,末端关节总偏角为49°,图12(b)中各关节偏角α=10°,β=0°,末端关节总偏角为70°。实验结果表明,机械臂可在以基座中心为圆心的任意圆周方向完成平面弯曲运动,进一步验证了所构建解耦运动方程的正确性及控制系统可行性。