基于路径特征点算法的机械臂跟踪目标轨迹优化

张 凯, 蒋新军, 孙德全, 刘石林

(1.郑州旅游职业学院 机电工程学院,郑州 451464,E-mail: zhangkaizztrc@163.com;2.开封技师学院 智能制造学院,河南 开封 475004;3.河南科技大学 机电工程学院,河南 洛阳 471000)

为机械臂确定目标轨迹时可以采用试教法来实现,之后再以轨迹规划方法计算得到关节速度曲线[1-2]。采用传统轨迹规划算法进行分析时只考虑机械臂动力控制过程的非线性特征与电机转速的制约,按照这一方式导致规划轨迹无法完全发挥出机械臂应有的控制性能[3]。因此需要通过二次规划方法来优化目标轨迹,使机械臂达到更快运动速度,大幅缩短算法处理时间。相对传统形式的轨迹规划方法,根据动力学模型构建的轨迹规划算法可以充分发挥机械臂的运动学与动力控制过程非线性,同时考虑关节速率与载荷制约条件,确保规划轨迹可以有效发挥机械臂的驱动作用,同时也需注意上述算法需要对大量数据进行计算,整体效率偏低[4-7]。

现阶段,可以对机械臂动力学模型进行轨迹规划的算法通常选择相平面法,设置路径参数后,再转换机械臂运动学与动力学模型参数,通过对路径参数进行二阶微分计算构建路径参数化的动力仿真模型,之后建立路径参数模型,使关节速率与力矩约束条件转换成路径约束条件,从而可以利用路径参数二维优化的方式来转换轨迹规划过程[8-9]。相平面法可以达到很高的处理效率,但缺乏良好的通用性,极大提高了约束难度,此外如果考虑加速度因素的制约时,将导致相平面法的计算过程更加复杂[10-11]。刘学成[12]通过相平面法测试非线性轮胎动力学特点的车辆模型控制过程稳定状态,再根据失稳度指标构建得到由模糊神经网络与PID算法共同调节的模型来达到车辆稳定操纵的效果。通过仿真测试可知,采用本文控制方案可以促进车辆操纵稳定性的显著提升。孙晓军[13]则利用速度特征点和修型射靶算法来调整优化最初的轨迹参数,保证经过修形处理的目标轨迹达到关节速度与力/力矩限制条件,形成了光滑过渡的速度曲线。通过测试可知,上述轨迹规划算法对各类目标轨迹都实现了理想规划效果,可以获得满足连续平滑性能的最优轨迹。

本文选择相平面法设置速度曲线,同时利用相平面法调节的方式使算法达到更高处理效率,通过轨迹平滑处理的方式来达到稳定控制机械臂运动状态的效果。

1 路径特征点算法

需为机械臂目标轨迹提前设置路径点向量P,根据运动学逆计算的方法获得关节向量q。为保证可以在各路径点处都实现机械臂的平稳控制,选择B样条曲线完成路径点向量的插值计算并确定目标轨迹。进行二次规划时需对目标轨迹实施离散化计算,使轨迹转换成稀疏离散化过程。当设置位姿向量的序列太小时则无法全面保留目标轨迹,造成一定程度的失真。因此根据目标轨迹路径复杂性和动力学模型来提取获得目标轨迹路径参数,进行路径参数计算时则通过模糊推理的方式完成,按照等间距的条件得到路径特征参数[14-15]。

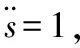
(1)

运用式(1)建立重力加速度向量如下:

(2)

γg=a4=[JT]-1G{Z-1[f(s)]}

(3)

图1给出了路径特征算法具体流程,如下所示。

2 实验

2.1 实验方案

为了判断速度曲线规划算法可靠性,本实验选择可以实现六自由度控制的攻角机械臂作为测试对象测定了轨迹规划算法处理效率与可靠性。图2为机械臂的具体结构,可以实现俯仰α、法向Y、轴向X、侧向Z的控制效果,将机械臂模型安装于滚转系统的末尾区域,表1给出了不同自由度下对应的力矩/电流与速度约束条件。

表1 关节约束表

PC系统通过人机交互界面软件进行运行状态监控时设置了MATLAB接口来实现轨迹调用,再把规划数据利用ADS通信的方式传递至工控机控制系统。通过工控机调节机械臂软件程序实现动作控制功能,可以精确调节机械臂位置参数并采集关节速度、电流等信息。通过接口实现算法调用后,再以DAS通信的方式把规划结果发动至工控机。在工控机中运行机械臂软件,实现位置与速度的调节并使其到达指定部位,同时采集获得速率参数。

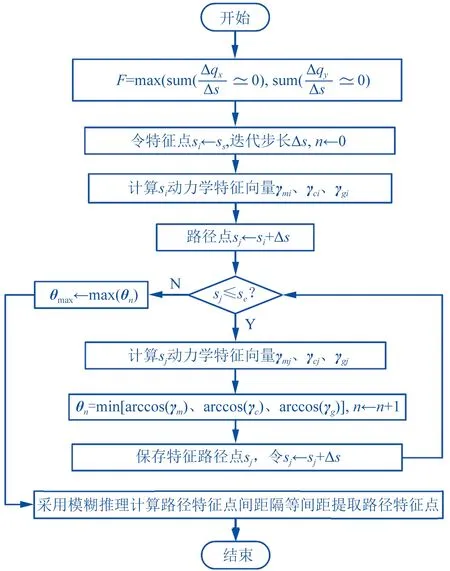
▲图1 路径特征点算法流程图

▲图2 机械臂结构示意图

2.2 算法有效性

为了对速度曲线规划算法进行可靠性验证,专门设置了轨迹规划测试方案。设定最初目标轨迹位置坐标为(-400 mm,-150 mm,0 mm)T以及终点坐标(0 mm,500 mm,0 mm)T,并以B样条差插值的方式使初始与终止位置之间形成连续轨迹。根据动力学特征参数提取得到有限数量的路径特征参数,图3给出了不同路径特征点对应的自由度结果。

▲图3 路径特征点分布

计算得到不同时间对应的速度曲线与加速度曲线,具体见图4-5。可以明显发现此时形成了平滑过渡的速度曲线,未产生突变的情况,加速度曲线除启动和停止阶段为实现加速、减速控制性能需保持加速度不为零的条件以外,其余时间都呈现连续平滑的状态。根据以上研究结果可知,规划获得的速度曲线能够达到连续光滑的性能要求。

▲图4 轨迹t-相平面

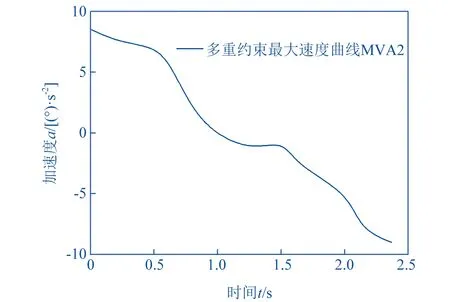
▲图5 轨迹相平面

图6与图7给出了不同时间下的机械臂自由度关节位置q及其速度/角速度,可以看到此时形成了与预期相符的连续分布关节位置与速度曲线。

▲图6 关节位置曲线

▲图7 关节速度曲线

对于伺服电机驱动力矩可以通过驱动电流与扭矩系数相乘的方式得到,同时为简化计算过程,以驱动电流判断机械臂处于不同自由度下的目标轨迹跟踪性能。使机械臂与所有关节时间序列形成精确跟踪的状态,图8给出了关节驱动电路示意图,可以明显发现,机械臂与Q1曲线之间保持紧密跟踪状态,X自由度驱动电流与额定电流的边界参数相近,其余自由度都比额定电流边界更低,表明规划得到的最大速度曲线与加速度/力矩条件相符,可以有效实现机械臂驱动功能。

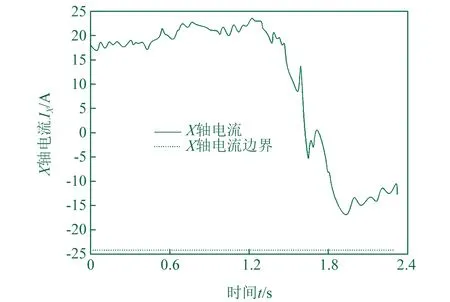
▲图8 关节电流曲线

2.3 算法计算效率分析

2.3.1 路径特征点数目优化

当选择不同数量路径特征点序列的情况下对于轨迹规划算法效率和可靠性也存在明显影响。没有选择路径特征点算法的条件下,由路径特征点组成序列集,同时受到路径的复杂性与机械臂的非线性结构影响。本实验进行路径特征点算法片评价时选择路径复杂性与机械臂的非线性状态作为评价指标,经模糊计算确定路径特征点的间距区间为(0,1),之后通过等间距方式提取得到路径特征点,实际测试结果也不受目标轨迹路径点数量的影响。图9给出了分别使用路径特征点和未使用路径特征点算法时来规划复杂目标轨迹时所需的计算耗时,结果显示随着路径点数量增加后,会导致算法时间的明显延长,设置太多路径点数量的条件下以路径特征点算法处理时可以实现算法效率的显著提升。

▲图9 算法效率统计

以速度曲线规划算法进行处理的步骤如下:形成连续路径轨迹后与采集路径特征点参数T1、建立多重约束最大速度曲线T2、曲线优化T3。

对表2结果进行分析可以发现,未优化的条件下采集得到的多重约束最大速度曲线T2占用了最大比例的处理时间,尤其是处理复杂目标轨迹规划时相对简单目标轨迹需要占用更长时间。经过优化处理后,多重约束最大速度曲线T2时间明显缩短。以上结果表明,以加速度为0的速度曲线取代Q1时,整个计算过程所需的规划时间能够大幅缩短。

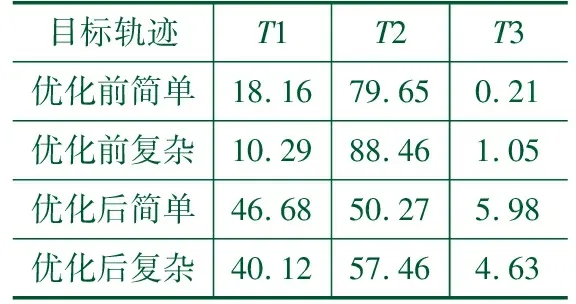
表2 轨迹规划算法计算时间/%

2.3.2 算法对比

为了进一步验证本文轨迹规划算法具备比其它轨迹规划算法更优的处理效果,分别以不同算法测试了简单与复杂轨迹处理效率,得到表3所示的参数。可以明显看到,采用本文设计的轨迹规划算法可以获得比其它路径规划算法更短的耗时,而遗传算法消耗了最长的时间。

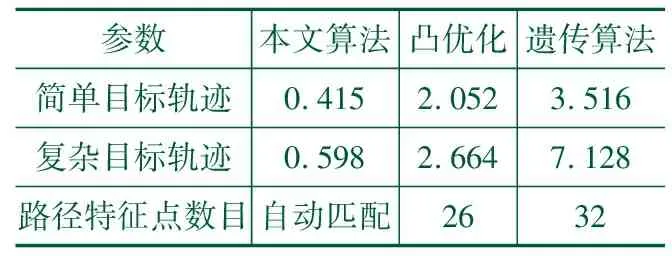
表3 计算效率结果对比

以上研究结果表明,速度曲线规划算法具备比凸优化算法与遗传算法更快处理效率,同时也受到路径复杂性的直接影响,随着路径复杂度的提高,需要消耗更长的规划时间;路径点数量则是规划算法的一个最关键影响因素,当路径点太多时将会造成轨迹规划效率的下降。

3 结论

(1) 形成了平滑过渡的速度和加速度曲线,获得的速度曲线能够达到连续光滑的性能要求。规划得到的最大速度曲线与加速度/力矩条件相符,可以有效实现机械臂驱动功能。

(2) 随着路径点数量增加,算法时间明显延长,设置太多路径点可以实现算法效率的显著提升。以加速度为0的速度曲线取代Q1时,整个计算过程所需的规划时间能够大幅缩短。

(3) 采用本文算法可以获得比其它路径规划算法更短的耗时,且更适合于复杂路径。