可更换抗侧耗能装置的钢框架结构地震易损性分析*
2023-07-25张爱林姜子钦张文莹杨晓峰
张爱林 杨 硕 姜子钦,2 张文莹 刘 杰 杨晓峰
(1.北京工业大学建筑工程学院, 北京 100124; 2.北京工业大学, 北京市高层和大跨度预应力钢结构工程技术研究中心, 北京 100124; 3.北京建筑大学, 北京未来城市设计高精尖创新中心, 北京 100044)
0 引 言
近二十年来我国相继发生多次强震,造成了大量的人员伤亡和房屋损坏,直接经济损失高达数千亿元。以汶川地震为例,震中区建筑损毁率达到90%以上,损坏建筑基本都无法修复,故历次震害和社会发展对建筑结构抗震提出了新的需求。可恢复功能装配式钢结构基于可恢复功能抗震理念[1-3],在保护生命的前提下,使得结构中不宜更换的主体构件是无损伤的,塑性损伤只发生在易更换的低成本构件上,震后结构能继续具有足够承载能力,修复后的结构也能继续保持原结构的抗震性能,继续保护人民的生命财产安全。
国内外学者对可恢复功能结构中的可更换构件/部件结构进行了深入研究。Mansour等设计了一种可更换剪切连接件的偏心支撑钢框架结构,并对该结构的可更换性进行了研究[4]。Castiglioni等设计了一种可更换耗能元件的钢框架结构,旨在将结构在地震作用下的损坏全部集中于可更换的耗能元件上[5]。吕西林等提出了一种带可更换连梁的双肢剪力墙,通过试验对比了该剪力墙与普通剪力墙在抗侧承载力、耗能能力等方面的差别[6]。陈以一等提出了一种适用于抗弯钢框架的可更换组合梁连接构造[7],试验研究表明,该构造可以将损伤集中在钢梁翼缘处的角钢上,便于震后更换。刘阳等提出一种在柱脚设置可更换消能件的震损可更换组合柱,通过试验研究了该组合柱的可更换性[8]。张爱林课题组提出了一种新型可恢复功能装配式梁柱节点,并进行了翼缘盖板厚度、螺栓数量等不同参数下的试验研究[9-10]。同时还提出了一种可更换抗侧耗能装置的柱脚节点,并进行了修复试验[11-13],试验表明,该柱脚受损伤的抗侧剪切件可实现原位更换,且更换前后柱脚均具有良好的抗震性能。以上研究工作表明,可恢复功能装配式钢结构与传统钢框架结构在传力路径以及耗能方式等方面均存在明显差异,可以实现震后功能恢复。为充分了解可恢复功能装配式钢框架结构的抗倒塌性能,针对该结构进行易损性评估以推动其发展具有重要意义。
结构的地震易损性是指在不同强度地震动作用下结构在某种极限状态的失效概率,是预测结构地震震害的基础。近年来,国内外学者对结构地震易损性做了大量研究。吕大刚等通过建立局部地震易损性可靠度的表达式和结构可靠指标对局部性能指标参数的灵敏度表达式,提出了一种能极大提高结构地震易损性计算效率的方法[14]。Nasserasadi基于随机理论,对传统的易损性函数进行了修正[15]。徐善华等对不同龄期锈蚀钢框架分别进行了增量动力分析,提出了锈蚀钢框架地震易损性评定方法[16]。朱凯铭等对考虑屈曲约束支撑疲劳性能的钢框架-支撑体系进行了易损性分析,对比了结构在单独主震和主余震序列作用下的地震易损性差异[17]。方成等对不同层数的自复位支撑钢框架分别进行了静力推覆分析、非线性时程分析和增量动力分析,提出了基于混合控制手段的自复位结构减控方法[18]。王伟等通过对多层梁贯通式支撑钢框架进行的IDA分析,定量评价了结构在不同节点刚度下的倒塌概率和抗倒塌储备系数[19]。通过学者们的研究可以得出结构地震易损性曲线是评价结构倒塌概率的有效手段。
首先对所研究的可更换抗侧耗能装置的钢框架结构体系构造进行介绍,而后建立可更换抗侧耗能装置的钢框架结构有限元模型,对该结构进行地震易损性分析,对比该结构与传统刚接框架结构的抗倒塌能力,最后分析不同参数对结构地震易损性的影响。
1 结构体系构造
可更换抗侧耗能装置的钢框架结构体系(LRED-SF)主要由工字梁、方钢管柱和可更换抗侧耗能装置的柱脚节点组成。其中可更换抗侧耗能装置的柱脚节点由方钢管柱、抗侧耗能装置及高强螺栓组成,抗侧耗能装置由节点板、柱脚横梁及抗侧剪切件焊接而成,如图1所示。可更换抗侧耗能装置的钢框架结构体系与传统刚接框架结构传力路径不同,可将结构内的塑性损伤集中在易于更换的抗侧耗能装置上,使梁、柱等主体构件基本处于弹性状态,震后只需更换抗侧耗能装置即可实现结构功能的快速恢复。
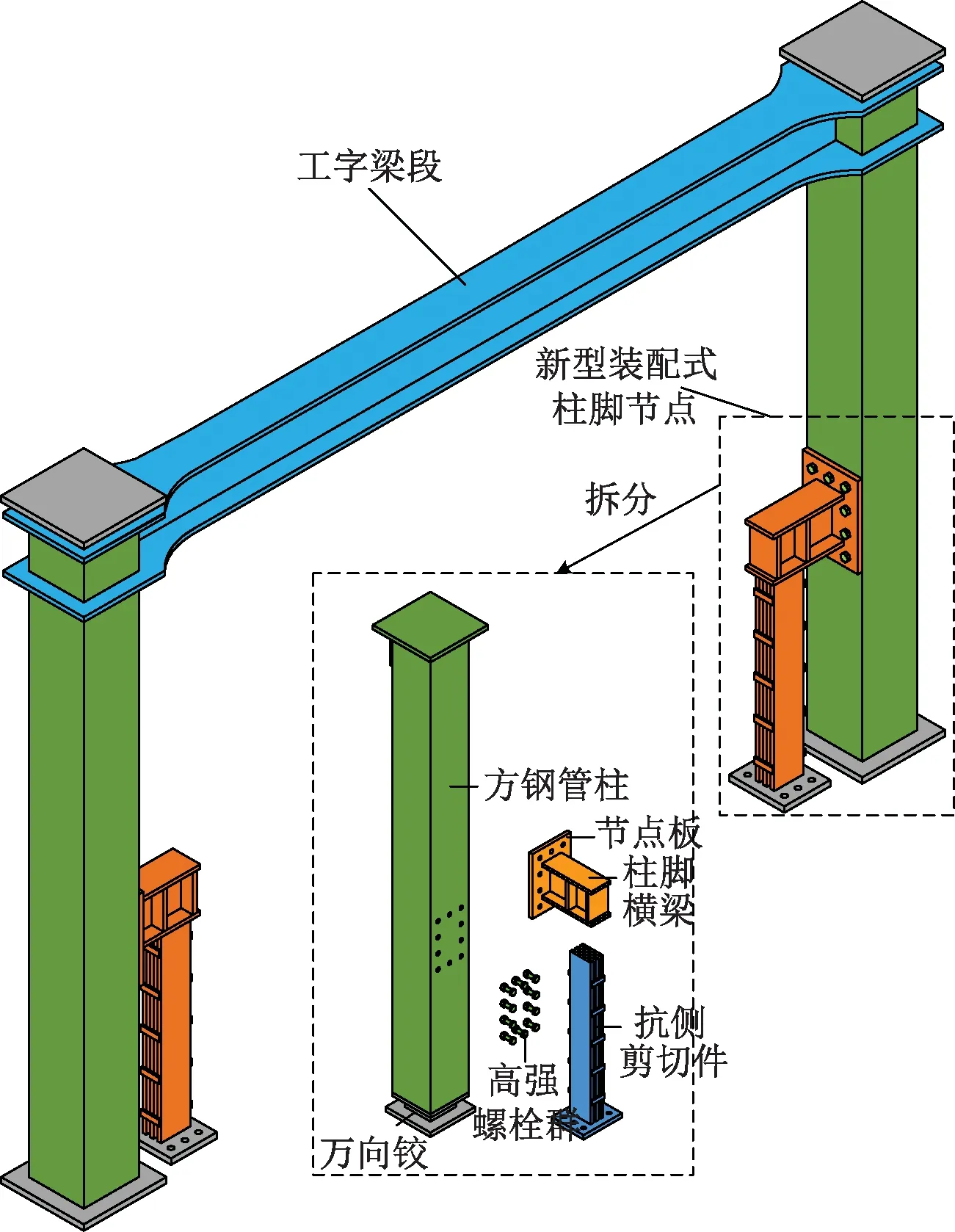
图1 可更换抗侧耗能装置的钢框架结构体系构造Fig.1 Structure of LRED-SF
2 结构分析模型的建立
2.1 柱脚节点的模型建立及正确性验证
2.1.1试验概况
课题组在此前已开展了可更换抗侧耗能装置的柱脚节点的低周往复荷载试验,对3个节点试件进行了5次拟静力低周往复试验研究[11],主要考察了柱脚节点的抗震性能、震后修复性能、疲劳性能以及抗侧剪切件截面参数变化对节点性能的影响,试件尺寸如图2所示,节点参数变化如表1所示。其中,bw、tw分别为抗侧剪切件单块钢板的宽度和厚度;lw为抗侧剪切件高度。

表1 节点试件参数变化Table 1 Dimensions of specimens mm
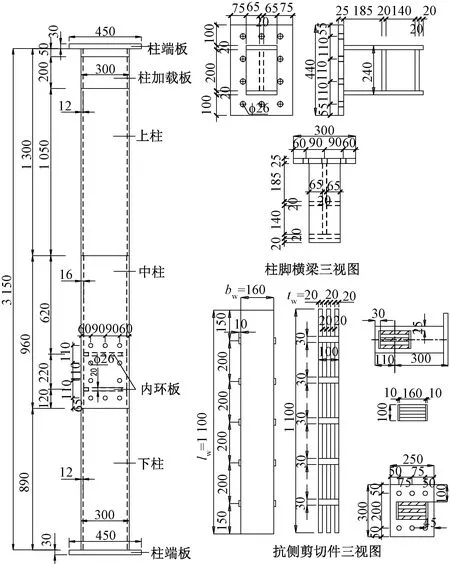
图2 试件尺寸 mmFig.2 Dimensions of specimens in detail
2.1.2模型建立
本文采用OpenSEES平台建立可更换抗侧耗能装置的柱脚节点有限元模型,根据第1节所述构造及特点,可更换抗侧耗能装置的柱脚节点的方钢管柱、柱脚横梁、抗侧剪切件采用Force-Based Beam-Column单元模拟,钢材本构采用Steel 02模型。柱脚节点有限元模型如图3所示。

图3 柱脚节点有限元模型Fig.3 Finite element model of column foot joints
2.1.3模型验证
为验证可更换抗侧耗能装置的柱脚节点数值模拟方法的合理性,对试件RGS1RR、RGS2、RGS3分别进行了模拟,其中RGS1RR是RGS1的修复试件。模拟过程中采用的构件尺寸、加载制度、边界条件、材性均与试验保持一致。模拟结果与试验结果的滞回曲线对比如图4所示,RGS1RR各加载级峰值点荷载对比如表2所示。可见:试件RGS1RR经历过两次修复试验,其滞回曲线与模拟存在一定差异,各加载级峰值点荷载误差在10%以内;试件RGS2和RGS3拟合效果与试验结果表现出较为一致的曲线走势及发展规律,且曲线整体吻合度较高,误差在合理范围内。整体来看,所建立的有限元模型可以较好地模拟柱脚节点的滞回行为。
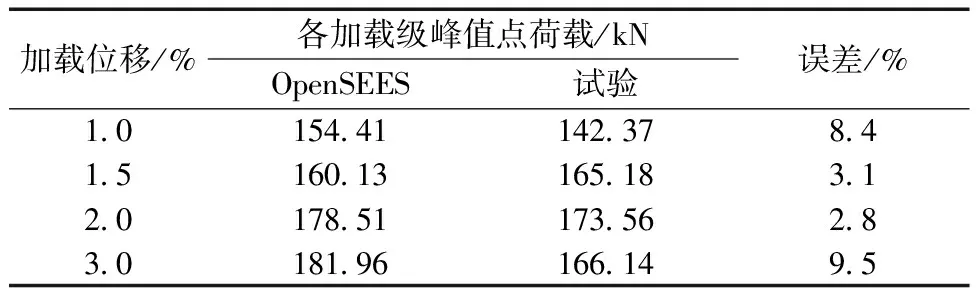
表2 RGS1RR各加载级峰值点荷载Table 2 Peak load of each loading stage in RGS1RR

a—RGS1RR; b—RGS2; c—RGS3。图4 滞回曲线对比Fig.4 Comparison of hysteresis curves
2.2 可更换抗侧耗能装置的钢框架模型建立
目前传统刚接框架结构(RSF)在国内外已经得到了广泛的应用,为此根据相关规范设计了一个普通刚接框架。模型的主要设计参数如下:抗震设防烈度为8度,设计基本地震加速度为0.2g,设计地震分组为第一组,场地类别为Ⅱ类,结构为6 层,层高均为3 m,结构平面尺寸为12 m×24 m,梁、柱的钢材等级均采用Q345B,梁、柱截面尺寸见表3。屋面恒、活荷载分别为6 kN/m2和0.5 kN/m2,楼面恒、活荷载分别为5 kN/m2和2 kN/m2,由于层数较低,故不考虑风荷载作用。重力荷载代表值按“1.0恒载+0.5活载”计算。

表3 构件截面尺寸Table 3 Dimensions of members mm
以传统刚接框架结构(RSF)为基础,基于课题组柱脚节点理论设计方法,按照与传统刚接柱脚等效的设计原则设计了一个可更换抗侧耗能装置的钢框架,其中底层柱采用变截面方钢管柱,上柱及下柱截面为300 mm×12 mm,中柱截面为300 mm×16 mm,中柱段长度为960 mm。可更换的抗侧耗能装置附加在底层柱上,其中柱脚横梁规格为240 mm×150 mm×20 mm×20 mm,抗侧剪切件采用160 mm×20 mm×1 000 mm的3块钢板组合而成,板件间距为20 mm。抗侧剪切件采用Q235B钢,方钢管柱与柱脚横梁等其余构件均采用Q345B钢。可更换抗侧耗能装置的钢框架结构2~6层梁柱构件尺寸和材性与传统刚接框架相同。模型立面如图5所示。
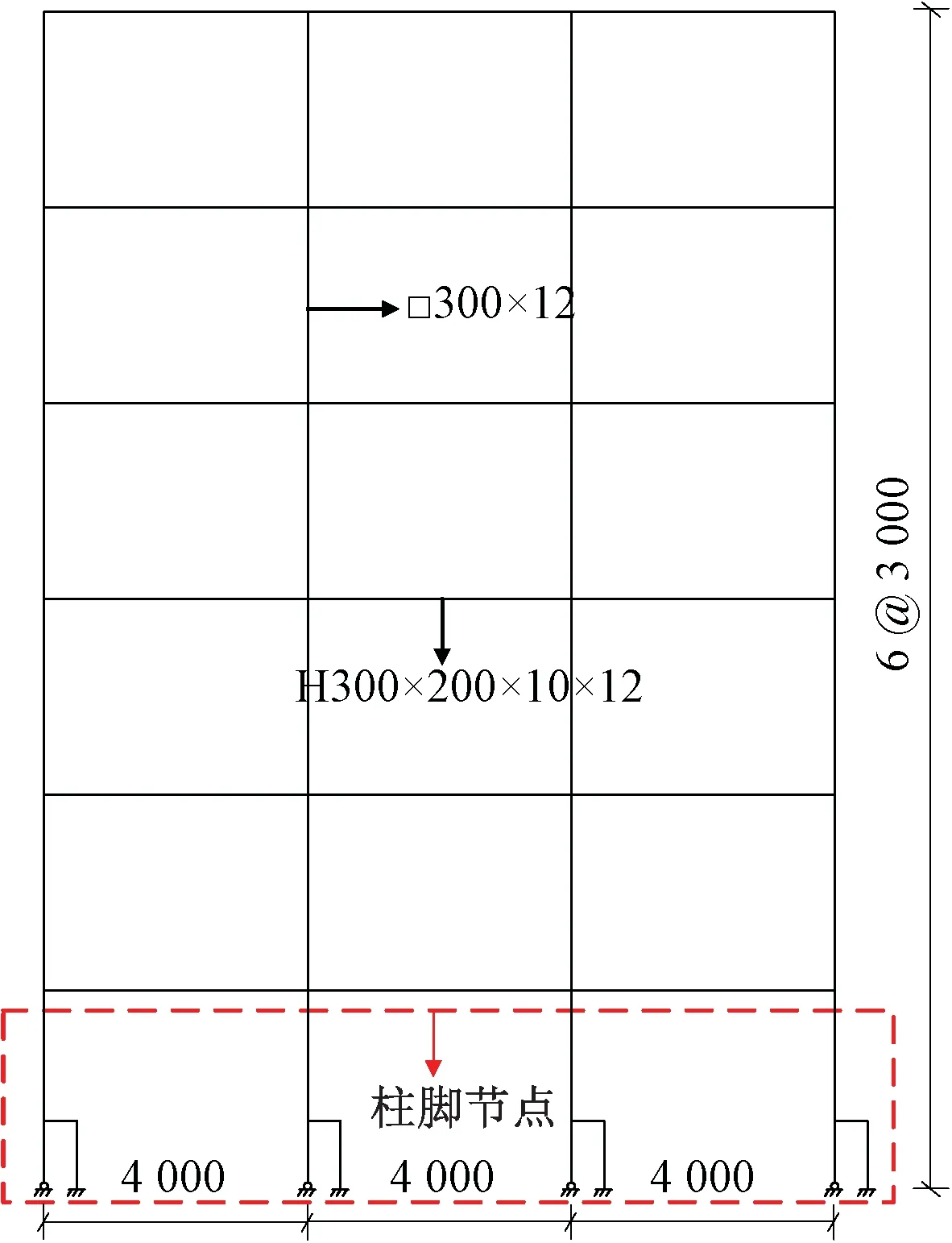
图5 LRED-SF立面 mmFig.5 Front view of LRED-SF
采用OpenSEES建立可更换抗侧耗能装置的钢框架结构数值分析模型,底层柱以及柱脚节点采用2.1节所述方法建立,2~6层梁柱单元采用Displacement-Based Beam-Column单元进行模拟,钢材采用Steel02材料模型。
3 地震易损性分析
3.1 地震动记录的选取
由于地震发生具有随机性和不确定性,每条地震波都有独特的参数,因此需要选取适合工程场地和抗震设防烈度的地震波,使其对结构有针对性。研究表明[20],通常情况下,对于中等高度的建筑,选取合适的地震动强度指标和10~20条地震动记录就能准确评估出结构的抗震性能。因此选取FEMA P695报告建议的22条远场地震波对结构进行增量动力分析。所选地震动加速度反应谱如图6所示。
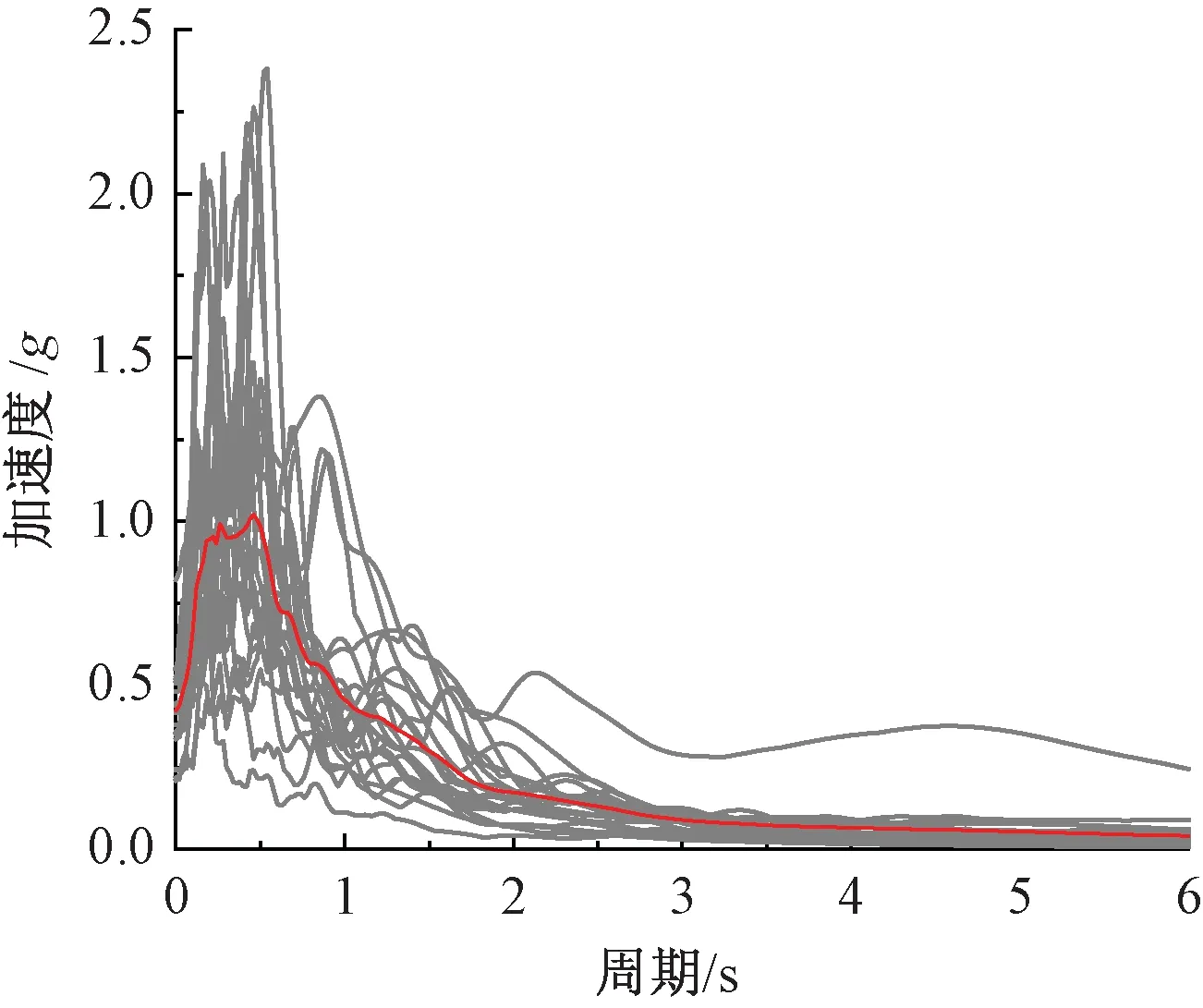
图6 所选地震动加速度反应谱Fig.6 Acceleration response spectrum of selected seismic waves
3.2 指标选取和极限状态的确定
结构的损伤指标(DM)是评价结构性能状态的重要参数。最大层间位移角可以反映节点的损伤、主体构件的破坏程度和结构的层间位移延性等,故选取最大层间位移角θmax作为结构的损伤指标来进行IDA 分析。
地震动强度指标(IM)是衡量地面运动剧烈程度的重要参数。由于Sa(T1,5%)作为地震动强度指标时IDA曲线离散性小,结构性能评估较为准确,因此选取Sa(T1,5%)作为地震动强度指标。
结合相关规范及柱脚节点的相关试验研究成果,总结得到LRED-SF不同性能水平的层间位移角限值和各破坏等级与性能水平之间的关系,分别如表4和表5所示。

表4 不同性能水平的层间位移角限值Table 4 Inter-storey drift angle limits for differentperformance levels %
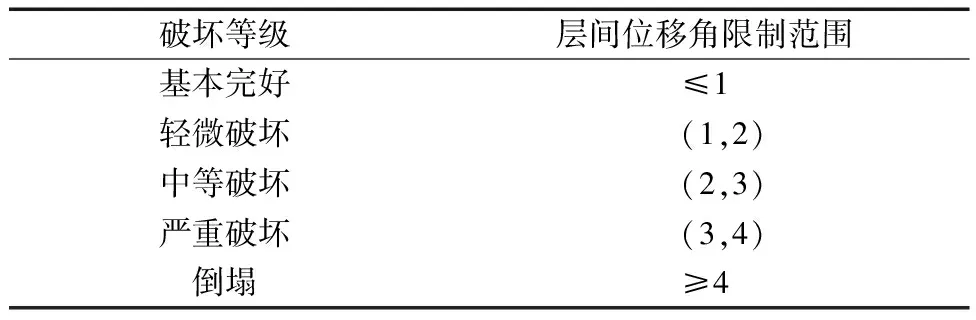
表5 破坏等级与性能水平之间的关系Table 5 Relationship between failure level and performance level %
3.3 IDA分析
分别对所选22条地震波的Sa(T1,5%)进行调幅,对模型进行不同地震动强度下的非线性动力时程分析,记录分析过程中IM和DM值,直至结构达到倒塌性能点,即可认为结构发生倒塌,终止分析。
图7为两结构的IDA曲线。可以看出:当地震动强度较小时,曲线未见明显离散,基本呈线性上升趋势,此时结构处于“小震不坏”的弹性阶段,地震波的随机性和不确定性对结构性能影响较小。随着地震动强度的增大,结构最大层间位移角约为2%时,曲线斜率逐渐减小,出现了离散,结构部分构件在地震动作用下由弹性阶段进入塑性阶段。随着地震动的再次增强,曲线斜率降低趋势加剧,离散性也随之增加,地震动的随机性和不确定性对结构弹塑性的发展影响显著。有些曲线的斜率出现了增长,这是因为结构中部分构件进入强化阶段。随着地震动的再次增强,曲线斜率出现大幅度降低。当结构达到倒塌性能点时,认为结构处于倒塌边缘或已经发生倒塌,终止分析。
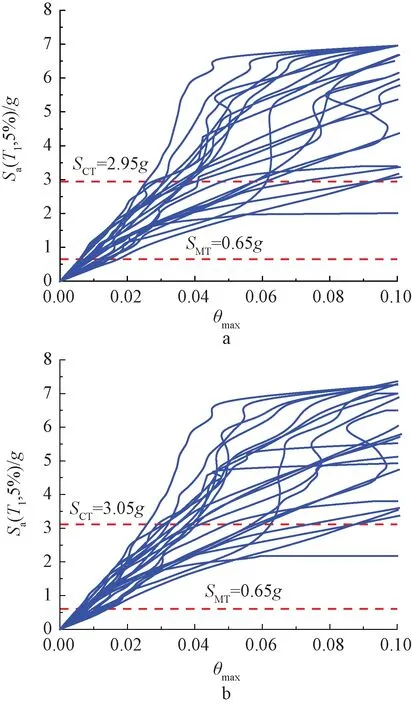
a—RSF; b—LRED-SF。图7 结构IDA曲线Fig.7 Structural IDA curves
两种结构的16%、50%以及84%分位IDA曲线如图8所示。两个模型50%分位IDA曲线极限状态汇总如表6所示。对于RSF,θmax=0.02时,50%的地震动记录Sa(T1,5%)≤1.512g。对于LRED-SF,θmax=0.02时,50%的地震动记录Sa(T1,5%)≤1.554g,可以看出LRED-SF的抗震性能优于RSF。

表6 50%分位IDA曲线极限状态Table 6 Limit state of 50% percentile IDA curves

a—RSF; b—LRED-SF。图8 16%、50%和84%的IDA曲线Fig.8 16%、50% and 84% percentile IDA curves
3.4 地震概率需求模型和地震易损性曲线
研究表明[21],结构损伤指标(DM)与地震动强度指标(IM)之间的关系满足式(1):
DM=α(IM)β
(1)
式中:α、β为拟合系数。
将结构损伤指标θmax与地震动强度指标Sa(T1,5%)代入式(1),然后两边取对数可以得到式(2):
lnθmax=a+blnSa(T1,5%)
(2)
其中a=lnα,b=β
结合之前IDA分析的数据,建立以lnSa(T1,5%)为横坐标,lnθmax为纵坐标的坐标系,得到一系列离散的点,对这些点进行线性回归分析,得到如图9所示的地震概率需求模型。从地震概率需求模型中提取a和b,进而可以换算得到α和β。
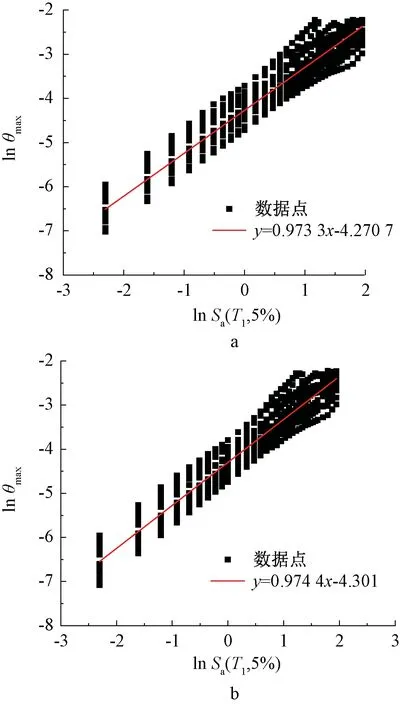
a—RSF; b—LRED-SF。图9 地震概率需求模型Fig.9 Seismic probabilistic demand model
结构的地震易损性表示在不同的强度地震作用下结构地震反应D超过相应极限状态下的结构能力C的条件概率。可表示为式(3):
(3)
由于C、D为独立随机变量,且它们都服从正态分布,故结构在各极限状态下的失效概率可以表示为:
(4)
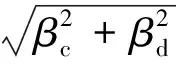
两结构的地震易损性曲线如图10所示。可以看出:当地震动强度较小时,结构在正常使用状态下的失效概率急剧上升,易损性曲线的斜率较大,说明结构由弹性阶段进入弹塑性阶段的速度较快。随着地震动强度的增大,结构在不同极限状态下的失效概率逐渐增大,即结构的易损性增大。当Sa(T1,5%)=1.0g时,RSF结构在正常使用极限状态下的失效概率是79.85%,在立即使用极限状态下的失效概率是18.49%,在生命安全极限状态下的失效概率是2.81%,在防止倒塌极限状态下的失效概率是0.43%;LRED-SF结构在正常使用极限状态下的失效概率是77.65%,在立即使用极限状态下的失效概率是16.54%,在生命安全极限状态下的失效概率是2.35%,在防止倒塌极限状态下的失效概率是0.34%,可以得出,LRED-SF结构的失效概率始终位于RSF结构之下,LRED-SF结构的抗倒塌性能优于RSF。可更换抗侧耗能装置的柱脚节点是基于与刚接柱脚节点等效原则设计的,故将其放入钢框架后组成的LRED-SF应与刚接框架结构等效,即可更换抗侧耗能装置的钢框架结构的屈服荷载及初始刚度应等于或略大于对应刚接框架结构,对比图中易损性曲线可以看出,可更换抗侧耗能装置的钢框架结构完全符合等效设计原则,可用该结构等效代替对应刚接结构。
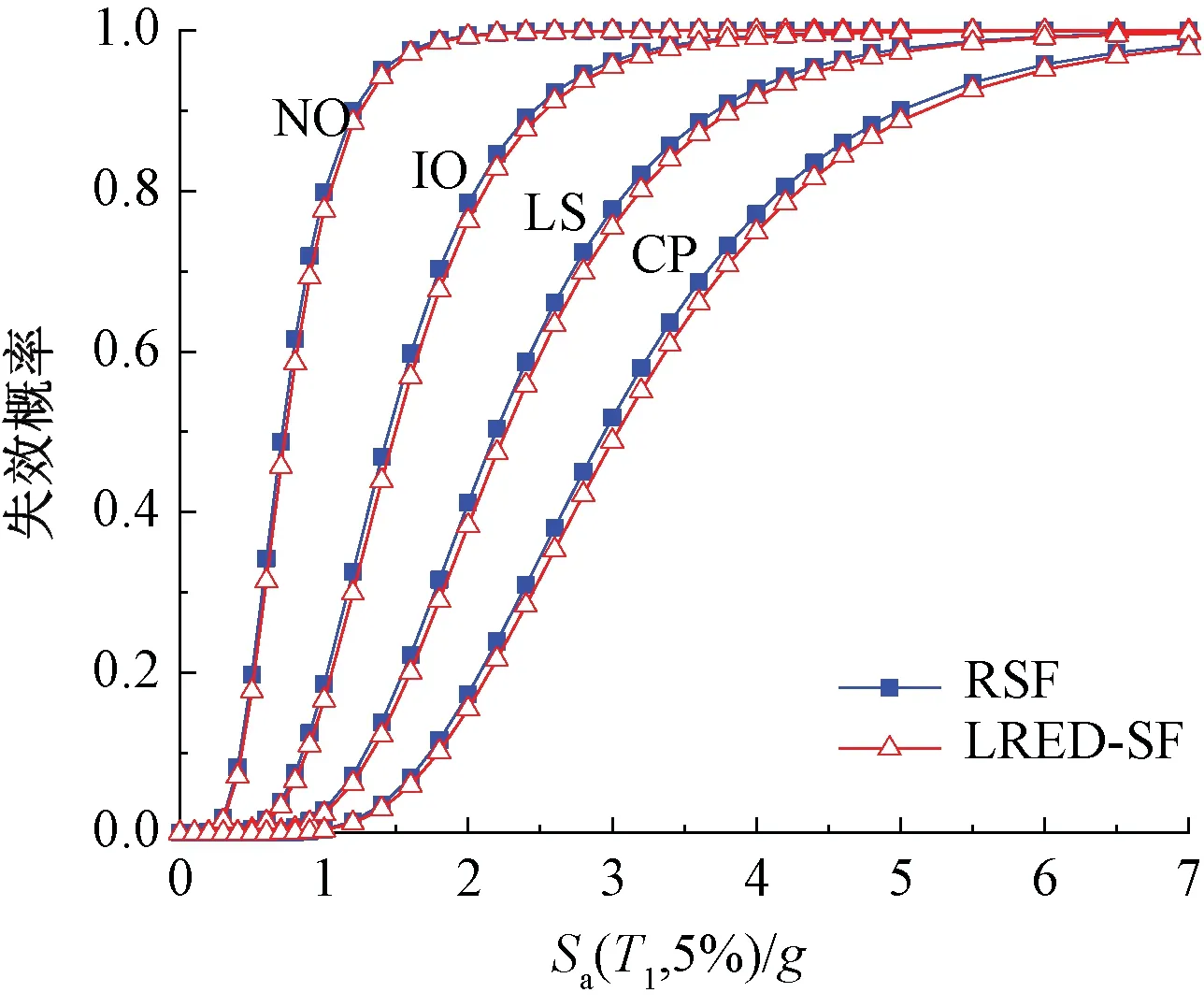
图10 地震易损性曲线Fig.10 Seismic fragility curve
3.5 抗倒塌储备系数
FEMA P695报告中建议采用抗倒塌储备系数(CMR)作为结构抗倒塌能力的评价指标,其计算公式为:
(5)
式中:SCT为中值倒塌谱的加速度;SMT为考虑最大地震的地震动强度。根据地震易损性曲线可得两结构的抗倒塌储备系数,如表7所示。可以看出,两个结构均具有较高的抗倒塌安全储备能力,按照GB 50011—2010《建筑抗震设计规范》设计的可更换抗侧耗能装置的钢框架结构可以满足结构抗震性能要求。LRED-SF的CMR相比RSF提高了3.5%,即LRED-SF的抗倒塌能力比RSF更强。

表7 结构抗倒塌储备系数Table 7 Collapse margin ratio
4 结构地震易损性影响因素分析
为充分研究可更换抗侧耗能装置的钢框架结构的抗倒塌性能,围绕抗侧剪切件宽度bw、单片钢板厚度tw及柱脚横梁刚度比ψbw对可更换抗侧耗能装置的钢框架结构的地震易损性进行变参数分析。各组算例模型主要参数如表8所示。

表8 各算例模型主要参数Table 8 Main parameters of numerical models
不同参数对LRED-SF结构倒塌极限状态易损性曲线的影响如图11所示。从图11a可以看出,随着抗侧剪切件宽度的增加,柱脚节点承载力增大,LRED-SF结构在防止倒塌极限状态下的失效概率降低,但是当增加到190 mm时,结构的失效概率增加,说明LRED-SF结构的抗倒塌能力与抗侧剪切件宽度的变化关系并不是线性的,当抗侧剪切件宽度增加到一定程度时,结构抗倒塌能力会下降。从图11b可以看出,抗侧剪切件单片钢板厚度的变化对结构的失效概率影响不显著,这是由于抗侧剪切件单片钢板厚度的变化范围是有限的,且可更换抗侧耗能装置的柱脚节点的主要失效模式为抗侧剪切件与柱脚横梁处发生断裂,这与厚度无关。从图11c可以看出,随着柱脚横梁刚度比的增加,结构在防止倒塌极限状态下的失效概率降低,这是由于柱脚横梁刚度越大,其对抗侧剪切件约束越明显,节点承载力越高。
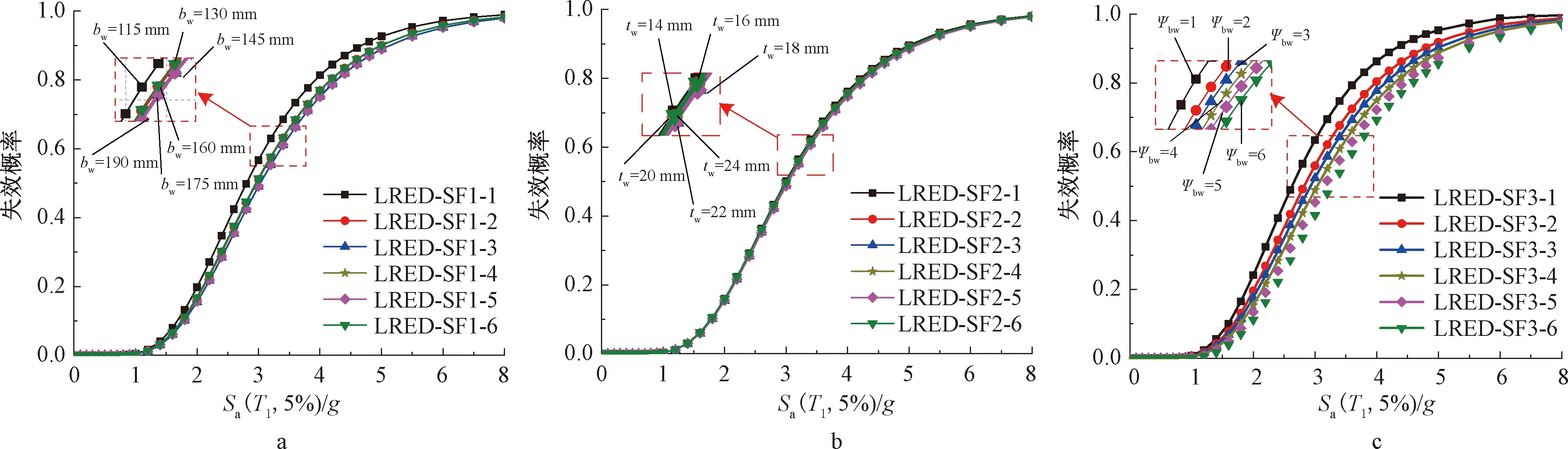
a—抗侧剪切件截面宽度; b—抗侧剪切件截面厚度; c—柱脚横梁刚度比。图11 不同参数对结构倒塌极限状态易损性曲线的影响Fig.11 Influence of different parameters on vulnerability curve of CP
5 结束语
本文基于IDA方法对传统刚接框架(RSF)和可更换抗侧耗能装置的钢框架结构(LRED-SF)进行地震易损性分析,相关结论如下:
1)所建立的柱脚节点有限元模型可以较好地模拟柱脚节点的滞回行为。
2)按照GB 50011—2010设计的可更换抗侧耗能装置的钢框架结构可以满足结构抗震性能要求,而且该结构在不同极限状态下的失效概率均低于传统刚接框架结构,其抗倒塌能力优于传统刚接框架结构。
3)柱脚节点抗侧剪切件宽度和柱脚横梁刚度比是影响可更换抗侧耗能装置的钢框架结构地震易损性的主要参数。抗侧剪切件宽度越大,结构在防止倒塌极限状态下的失效概率越低,结构抗倒塌能力越强,但当抗侧剪切件宽度增加到一定程度时,结构抗倒塌能力会下降;柱脚横梁刚度比越大,结构抗倒塌能力越强。
