支点摩擦对半圆弯曲试样应力强度因子影响研究
2023-07-25唐晓宇吕川黄诗渊
唐晓宇 吕川 黄诗渊


摘要:为探讨支点摩擦对直槽半圆盘三点弯曲(NSCB)试样应力强度因子的影响,采用有限元方法研究了无量纲裂缝长度a/R 、支点跨距S/2R及支点摩擦系数f 对无量纲应力强度因子YI的影响规律。结果表明:当a/R或S/2R一定时,随着f 的增大,YI逐渐减小并趋于稳定;当f一定时,YI随a/R或S/2R的增大而增大,且a/R或S/2R越大,YI受支点摩擦的影响越显著;考虑摩擦作用后,YI与S/2R 、a/R 、f的关系为多个不规则空间曲面,故根据图中曲線进行插值计算较为方便。最后根据研究成果对两种类岩石材料的I型断裂测试结果进行了误差修正。在室内三点弯曲I型断裂试验中,若将支点取为固定约束,需在应力强度因子标定中考虑支点的摩擦影响。
关 键 词:摩擦系数; 应力强度因子; 断裂韧度; 半圆弯曲试验
中图法分类号: TU45 文献标志码: ADOI:10.16232/j.cnki.1001-4179.2023.06.027
0 引 言
断裂韧度是评价含裂缝结构的重要力学指标[1]。I型断裂韧度定义为材料在静荷载作用下抵抗裂纹扩展的能力,是预测实际工程岩体性质的主要参数。在岩石断裂力学领域,相关的断裂测试方法很多,国际岩石力学与岩石工程学会(ISRM)先后提出了采用人字形切槽三点弯曲圆棒试样(CB)[2]、人字形切槽短圆棒试样(SR)[3]、人字形切槽巴西圆盘试样(CCNBD)[4]以及直槽半圆盘三点弯曲试样(NSCB)[5]来测试岩石的静态Ⅰ型断裂韧度。
其中,CB与SR均为“V”形切口试样,具有基于岩芯的特色[6],优点在于不需要预裂也不需要测定裂纹长度。但它的不足之处是试样在某一指定方向需要数量较大的整块岩芯,断裂时需要的载荷较小,加载系统较为复杂,短棒试件的制备较为繁琐且仅能进行Ⅰ型断裂测试。ISRM在1995年提出的CCNBD试样体积小,却具有较高的临界荷载、试样加载方便[7]以及对设备要求不高等优点,在很多方面都优于SR和CB试样。但同时CCNBD也有其缺点,比如它为一种复杂的三维构型,增加了研究者标定其无量纲应力强度因子值的困难[8]。
相比之下,ISRM于2014年提出的NSCB试样[9]具有如下显著优势:① 易于准备,采用以核心为基础的标本几何形式,要求仅为简单的夹具;② 破坏以拉伸为主;③ 可以同时测试断裂韧度和抗拉强度。
在三点弯曲加载时,试样底部两个支点通常是固定约束的,在支点完全固定时,试样与支点间的摩擦无法忽略。近年来,NSCB试样被广泛运用于岩石材料的I型断裂测试,但在I型应力强度因子KI标定时往往忽略了试样与支点间摩擦对计算结果的影响。为了准确评估材料的断裂韧度,有必要开展对支点摩擦作用的研究。
鉴于此,为查明支点摩擦对KI的影响,采用有限元方法建立了不同无量纲裂缝长度a/R、不同支撑跨度比S/2R的NSCB试样数值模型,研究了支点摩擦系数对KI的影响规律,并查明了支点摩擦对断裂韧度计算结果带来的误差。
1 NSCB试样数值模型
1.1 NSCB试样加载原理
NSCB试样的结构及加载示意图如图1所示。图中,R为试件半径,a是裂纹长度,B是试件厚度,S是底部支撑之间的距离(跨度),r是支座的半径,F是施加于试样的集中力。
根据线弹性断裂力学的K判据,当载荷F达到峰值Fmax时,NSCB试样的断裂韧度KIC值由式(1)确定。
式中:Fmax为加载点峰值荷载;YI是与试样几何形状相对应的无量纲应力强度因子。
1.2 NSCB试样有限元模型建立
采用ABAQUS软件中的围线积分法对NSCB试样的断裂力学参数KI进行计算分析。首先,在裂缝尖端处设置奇异单元(16节点),围绕奇异单元划分了4圈二次积分八节点四边形单元CPE8R,其余区域采用自由划分产生八节点四边形单元CPE8。
为了模拟NSCB试件的边界条件,将底部的两个支座完全固定(ux=uy=0),并限定顶部支座仅在垂直方向移动(ux=0),通过给顶部支撑施加竖直向下的集中力来给整个试件加载。将3个支座分别以离散刚体进行建模,并考虑支座与试样之间的接触摩擦。与以往直接施加荷载的方式相比,采用离散刚体建立支座模型能够反映实际支点与材料之间的摩擦系数。
图2给出了a/R=0.5,S/2R=0.5时NSCB试样网格划分模型,单元数为10 937,节点数为11 031。
1.3 应力强度因子计算方法
根据线弹性断裂力学理论,在笛卡尔坐标系中的裂缝端部附近应力场可表示为
按照本文对裂缝端部附近网格的划分方式,从第一个围线到第5个围线的应力强度因子的变化范围均在0.1%以内,说明模型计算结果具有较好的收敛性,本文直接使用第五个围线的模拟结果来计算NSCB试样的应力强度因子KI。
1.4 模型计算参数
计算分析之前,已经考虑过不同弹性模量、泊松比对无量纲应力强度因子的影响。结果表明,无论弹性模量(0.1 GPa~100 GPa)、泊松比(0.1~0.4)如何改变,仅影响位移场,并不会对无量纲应力强度因子带来任何影响。另外,Aliha等[10]和罗毅等[11]也对泊松比、弹性模量的影响进行了分析,所得到的结论与本文一致。
值得指出的是,在数值模拟中,采用的荷载F不同,试样的受力状态(应力强度因子)必然发生改变,但无量纲应力强度因子是不变的。而且,在具体试验中,相同试样结构(S/R、a/R、R)具有相同的无量纲应力强度因子YI,但由于导致其临界荷载Fmax受材料种类影响,所获取的KIC是不同的。
鉴于此,本文模型弹性模量E与泊松比ν分别取20 GPa和0.25(应力强度因子标定中采用的材料本构通常为线弹性),同时,控制B、R与F为常数,分别为:B=10 mm,R=50 mm,F=1 000 N。
1.5 模型合理性验证
Kuruppu[5]和Lim[12]均给出了NSCB试样的无量纲应力强度因子公式:
值得指出的是,裂缝过长和过短时,无量纲应力强度因子受试样几何特征及网格划分的影响显著,计算结果差异容易被放大。因此,应力强度因子公式通常存在一定适用范围:a/R=0.4~0.6、S/2R=0.5~0.8,材料越硬,支点间距S/2R建议取大值,反之则相反[9]。
为验证本文结果的合理性,将本文计算结果与前人結果进行了对比。从图3(a)可知,在建议范围内本文结果与前人结果趋势和数值均十分接近,当支点间距取小值时,本文结果稍低于Kuruppu和Lim的计算值,当支点间距取大值时,本文结果位于两者之间。
为验证本文结果的合理性,图3(b)和(c)中给出了本文结果与前人计算结果的误差值,误差值由式(7)计算:
本文计算结果与Lim的计算结果误差为0.78%~11.03%,与Kuruppu的计算结果误差为0.51%~5.81%。
可知,本文数值模型计算得到的趋势与前人基本一致,说明计算模型可用于进一步分析支点摩擦的影响分析。
1.6 计算方案
为探究支点摩擦对无量纲应力强度因子的影响,本文计算方案如下:考虑8种无量纲裂缝长度(a/R=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8)、4种支点间距(S/2R=0.5,0.6,0.7,0.8)及11种支点摩擦系数(f=0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0),共计352个模型。
2 数值试验结果分析
2.1 不同S/2R时支点摩擦对YI的影响
图4给出了不同S/2R时支点摩擦对无量纲应力强度因子YI的影响关系曲线。
从图4可知,随着f增大,YI逐渐减小,最后在一定f值时趋于恒定。产生该现象原因是由于支点与NSCB试样间存在摩擦作用,产生的摩擦力一定程度阻碍了裂缝的开裂,使得其起裂荷载更大,根据公式(8),起裂荷载越大,YI越小。
YI=2RBFπaKI(8)
此外还可发现,当无量纲裂缝长度a/R一定时,支点间距S/2R越大,试样YI越大,受支点摩擦的影响也越明显。以图4(d)为例,当S/2R=0.5时,摩擦系数f增加至0.5时YI就趋于恒定,而当S/2R=0.8时,摩擦系数f增加至0.8时YI才趋于定值。
不考虑支点摩擦前,S/2R=0.8对应的YI=21.02大于S/2R=0.5对应的YI=12.63,而考虑支点摩擦后,S/2R=0.8对应的YI将趋于0.33,反而小于S/2R=0.5对应的YI最终趋于的0.49。
综上可知,考虑支点摩擦后,无量纲应力强度因子YI逐渐减小,支点间距越大,YI受支点摩擦的影响更为显著。
2.2 不同a/R时支点摩擦对YI的影响
图5给出了不同a/R时支点摩擦对无量纲应力强度因子YI的影响关系曲线。
从图5可发现,当支点间距固定时,不同裂缝长度情况下的YI随f增大而减小,a/R越大,YI受支点摩擦的影响越大。以图5(d)为例,当a/R=0.2时,摩擦系数f增加至0.3时YI就趋于恒定,而当a/R=0.8时,摩擦系数f增加至0.8时YI才趋于定值。
不考虑支点摩擦前,a/R=0.2对应的YI=4.56小于a/R=0.8对应的YI=21.02,考虑支点摩擦后,a/R=0.2对应的YI最终趋于3.00,而a/R=0.8对应的YI趋于0.33,远小于前者。
综上可说明,考虑支点摩擦后,无量纲应力强度因子YI逐渐减小,裂缝长度越长,YI受支点摩擦的影响更为显著。
2.3 考虑支点摩擦的应力强度因子标定结果
通常地,传统的应力强度因子标定时不考虑支点摩擦作用,给出的标定结果曲线一般如图6(a)所示,YI~ a/R关系曲线通常是单调递增形式。
从图6(b)和(c)可知,考虑支点摩擦后,YI~a/R关系曲线形态会发生改变,随着f增加,曲线从单调递增形态变为先减小后增大形态,当f增大至一定值时,曲线变为单调递减形态。由此说明,支点摩擦对YI影响明显,在摩擦系数f较大时尤为明显。
传统应力强度因子标定公式中未考虑支点摩擦,其无量纲应力强度因子YI仅受两个变量控制,即S/2R和a/R,根据量纲分析,NSCB试样的应力强度因子具有以下形式[13]:
KI=Fπa2RBYI=Fπa2RBf(aR,S2R)(9)
从图7(a)中可明显看出,当固定a/R时,YI与S/2R呈良好线性关系,因此,式(9)可改变成以下形式:
利用以上方法即可较好拟合YI与S/2R、a/R的关系曲线,得到相对较为简洁的标定公式。
然而,考虑支点摩擦后,无量纲应力强度因子YI则由3个变量(S/2R、a/R、f)所控制。从图7(b)可发现,当固定a/R时,考虑摩擦的YI与S/2R并未呈现明显规律。
由图6可知,YI与S/2R、a/R、f的关系实际上是多个空间曲面,若按照每个空间曲面导出相应的曲面方程,所得到的拟合方程拟合系数受曲面规则程度和拟合方程参数决定。考虑支点摩擦后,形成的空间曲面并不规则,且不同摩擦系数f所对应的曲面方程形式存在差异。相对而言,直接给出不同情况下的标定结果曲线更为简便,在Ⅰ-Ⅱ复合型断裂试样的标定中通常也是采用此类做法[14]。
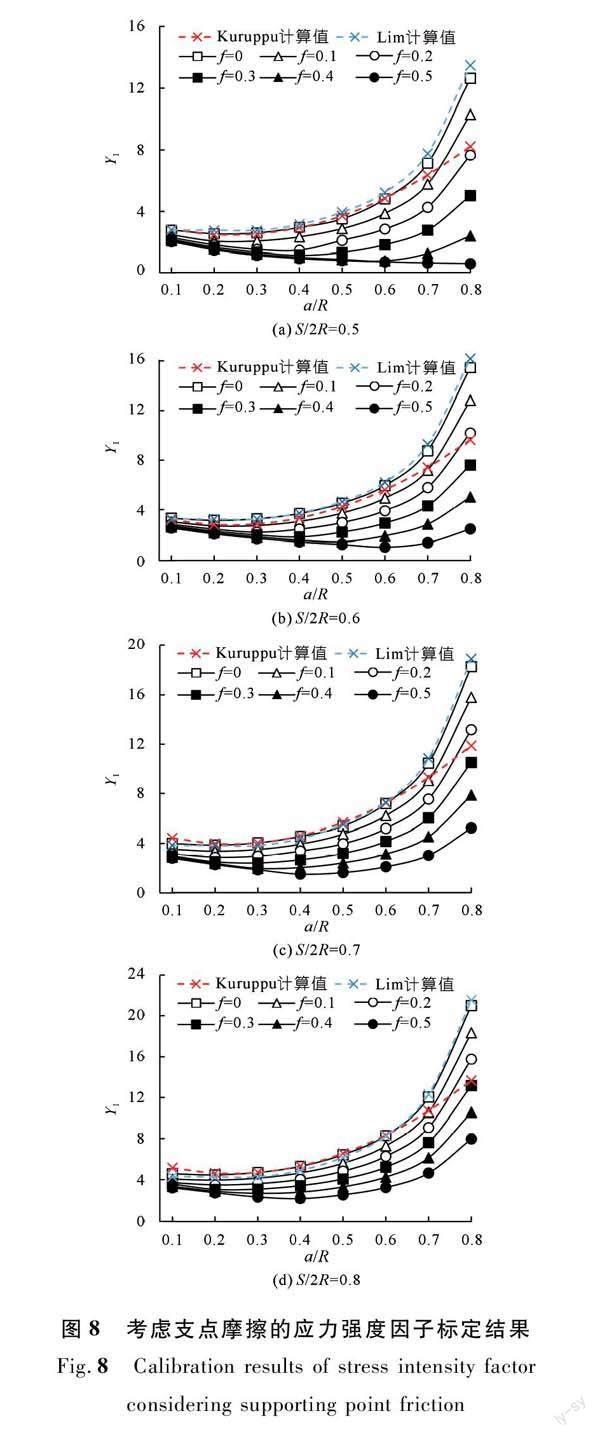
由图5的规律可知,支点间距S/2R越大,YI~a/R曲线趋于定值所需要的摩擦系数f就越大。鉴于此,本文给出了常用支点间距范围S/2R=0.5~0.8时的无量纲应力强度因子标定结果(见图8)。其中,以图8(a)为例,当摩擦系数f超过0.5之后,曲线基本保持不变,即若实际试验中支点摩擦系数f大于0.5,其仍可采用f=0.5对应的应力强度因子标定结果进行计算,若支点摩擦系数f小于0.5,则可根据图中曲线进行插值计算。
3 材料I型斷裂试验结果误差分析
3.1 考虑支点摩擦的应力强度因子误差分析
在室内三点弯曲加载试验中,底部支撑模具通常采用钢性材料制作,且通常对其进行固定约束。由于被测材料与钢之间存在摩擦系数,采用传统应力强度因子标定结果可能会过大估计材料的断裂韧度KIC。考虑支点摩擦后,误差可采用式(12)计算:
δ=YI考虑摩擦-YI不考虑摩擦YI不考虑摩擦(12)
以S/2R=0.8为例,考虑支点摩擦后应力强度因子的误差如图9所示。
当f=0.1时,不同a/R时对应的误差δ基本在12%左右,当f=0.2时,误差δ基本在23%左右。随着f 超过0.3后,误差δ则存在一定跨度,例如,当f=0.3时,误差δ为21%~37%,而当f=0.8时,误差δ则为34%~98%。根据前文结果可知,若支点跨径比S/2R取小值,计算所得到的误差则更大。
3.2 考虑支点摩擦的类岩石材料断裂韧度修正
笔者课题组前期针对类岩石材料压实黏土开展过一系列试验研究[15]。相对于岩石而言,压实黏土与钢之间的摩擦系数更大些。鉴于此,采用NSCB试样对压实黏土开展了I型断裂试验。
试验前,首先采用图10中所示方法测试了压实黏土与钢之间的摩擦系数,测试了12个试样(最大干密度、最优含水率状态)的摩擦系数,平均值为0.48。
根据前文可知,摩擦系数f相同时,无量纲裂缝长度a/R、跨径比S/2R均对无量纲应力强度因子产生影响。因此,选用了不同a/R和S/2R的压实黏土试样开展了试验,标准试样结构尺寸为:半径R=50 mm、厚度B=65 mm。图11为典型NSCB试样的断裂破坏过程,随着荷载的增加,裂缝端部宏观出现于预制裂缝端部,且发生自相似扩展,说明断裂破坏属于I型断裂模式。
从表1测试结果可发现,当跨径比S/2R相同时,随着a/R逐渐增加,不考虑支点摩擦计算得到的KIC逐渐减小,测试值在18.02~18.34 kPa·m0.5之间,而考虑支点摩擦计算得到的KIC在7.26~9.24 kPa·m0.5之间。当a/R相同时,随着跨径比S/2R逐渐增大,不考虑支点摩擦得到的KIC逐渐减小,测试值在18.02~26.05 kPa·m0.5之间,而考虑支点摩擦得到的KIC在6.21~7.26 kPa·m0.5之间。
同时,笔者收集了Bahrami对两种花岗岩I型断裂韧度测试的结果(支点固定约束)[16]。根据其文献描述,较硬花岗岩与钢的摩擦系数为0.14左右,而较软花岗岩与钢的摩擦系数为0.22左右。试验中选用的R=75 mm,a/R=0.53,S/2R=0.80。
如表2所列,若不考虑支点摩擦,则两种岩石的断裂韧度值分别为82.98,55.47 MPa·m0.5,考虑支点摩擦后,两者分别降至55.36,30.69 MPa·m0.5。
相对于压实黏土而言,岩石材料的断裂韧度量级大得多,忽略支点摩擦引起的误差比虽然差别不大,但实际差值则达到了数十MPa·m0.5。
由此可见,在室内三点弯曲I型断裂试验中,若底部两支点采用固定约束,在加载过程中由于试样与支点接触存在摩擦,所测得的峰值荷载中存在部分是为抵抗摩擦而产生,导致试验测得的KIC相对于真实值更大。
4 结 论
本文通过数值模拟研究了支点摩擦对NSCB试样应力强度因子的影响,并结合类岩石材料进行I型断裂实验误差分析,主要结论如下:
(1) 由于支点与NSCB试样间存在摩擦作用,当a/R一定时,随着f增大,YI逐渐减小,最后在一定f值时趋于恒定,且支点间距S/2R越大,试样的YI越大,受支点摩擦的影响也越明显。
(2) 考虑支点摩擦后,当S/2R固定时,随着f增大,YI逐渐减小,最后在一定f值时趋于恒定,且a/R越大,受支点摩擦的影响也越显著。
(3) 传统的应力强度因子标定时不考虑支点摩擦的作用,其YI~a/R关系曲线呈现较强规律性,可得出较简洁的标定公式,然而考虑摩擦后,YI与S/2R、a/R、f的关系实际上是多个空间曲面,此时直接根据标定曲线进行插值计算更为方便。
(4) 室内三点弯曲I型断裂试验中,若将支点固定约束,则测得的KIC实测值需要考虑支点摩擦的影响,否则将导致所测得的KIC实测值存在一定误差。
参考文献:
[1]李贺,尹光志,许江,等.岩石断裂力学[M].重庆:重庆大学出版社,1987.
[2]王启智,鲜学福.一种人字形切槽三点弯曲圆棒试样的应力强度因子算法[J].重庆大学学报(自然科学版),1991(4):20-24.
[3]王启智,鲜学福.人字形切槽短圆棒断裂韧度试样及其BEM标定[J].重庆大学学报(自然科学版),1991(3):55-59.
[4]XU C,FOWELL R J.Stress intensity factor evaluation for cracked chevron notched brazilian disc specimens[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1994,31(2):157-162.
[5]KURUPPU M D,CHONG K P.Fracture toughness testing of brittle materials using semi-circular bend(SCB)specimen[J].Engineering Fracture Mechanics,2012,91:133-150.
[6]张盛,李小军,李大伟.岩石Ⅰ型断裂韧度测试技术和理论研究综述[J].河南理工大学学报(自然科学版),2009,28(1):33-38.
[7]WANG Q Z.Stress intensity factors of the ISRM suggested CCNBD specimen used for mode-I fracture toughness determination[J].International Journal of Rock Mechanics and Mining Sciences,1998,35(7):977-982.
[8]张盛,王启智.用5种圆盘试件的劈裂试验确定岩石断裂韧度[J].岩土力学,2009,30(1):12-18.
[9]KURUPPU M D,OBARA Y,AYATOLLAHI M R,et al.ISRM-Suggested method for determining the mode I static fracture toughness using semi-circular bend specimen[J].Rock Mechanics and Rock Engineering,2014,47(1):267-274.
[10]ALIHA M R M,SAGHAFI H.The effects of thickness and Poisson′s ratio on 3D mixed-mode fracture[J].Engineering Fracture Mechanics,2013,98:15-28.
[11]罗毅,任利,谢凌志.岩石Ⅰ/Ⅱ复合断裂韧度测试的单边切槽深梁试件:数值分析与标定[J].岩石力学与工程学报,2016,35:3633-3643.
[12]LIM I L,JOHNSTON I W,CHOI S K.Stress intensity factors for semi-circular specimens under three-point bending[J].Engineering Fracture Mechanics,1993,44(3):363-382.
[13]胡凤辉.数值方法研究含裂纹半圆弯曲试验的应力强度因子[D].合肥:合肥工业大学,2014.
[14]ALIHA M R M,AYATOLLAHI M R.Two-parameter fracture analysis of SCB rock specimen under mixed mode loading[J].Engineering Fracture Mechanics,2013,103:115-123.
[15]WANG J J,HUANG S Y,GUO W L,et al.Experimental study on fracture toughness of a compacted clay using semi-circular bend specimen[J].Engineering Fracture Mechanics,2020,224:106814.
[16]BAHRAMI B,AYATOLLAHI M R,MIRZAEI A M,et al.Support type influence on rock fracture toughness measurement using semi-circular bending specimen[J].Rock Mechanics and Rock Engineering,2020,53(5):2175-2183.
(編辑:郑 毅)
Study on effect of supporting point friction on stress intensity factor of notched semi-circular bending specimen
TANG Xiaoyu1,LYU Chuan1,HUANG Shiyuan1,2
(1.Engineering Research Center of Diagnosis Technology and Instruments of Hydro-Construction,Chongqing Jiaotong University,Chongqing 400074,China; 2.State Key Laboratory of Mountain Bridge and Tunnel Engineering,Chongqing Jiaotong University,Chongqing 400074,China)
Abstract: In order to investigate the influence of supporting point friction on the stress intensity factor of Notched Semi-Circular Bending (NSCB) specimen samples,the finite element method was used to study the effects of supporting point friction coefficient (f) on the dimensionless stress intensity factor (YI) of NSCB specimens with different dimensionless crack lengths (a/R) and different supporting spans (S/2R).The results show that when a/R or S/2R is constant,YI will gradually decrease and tend to be stable with the increase of f. When f is constant,YI will increase with the increase of a/R or S/2R,and the larger a/R or S/2R is,the more significantly YI is affected by the supporting point friction.The relationship between YI and S/2R,a/R and f after considering friction were actually multiple irregular spatial surfaces,so it was more convenient to carry out interpolation calculation according to the curves in the figure.Finally,the error correction of the mode I fracture test results for two kinds of rock-like materials was carried out based on the calculated results.According to the results,in the mode I fracture of three-point bending test,if the supporting point was fixed,the supporting point friction should be considered in the stress intensity factor calibration.
Key words: friction coefficient;stress intensity factor;fracture toughness;semicircle bending test
收稿日期:2022-03-24
基金项目:国家自然科学基金项目(52109113);重庆市自然科学基金面上项目(cstc2021jcyj-msxmX1114);水利部堤防安全与病害防治工程技术研究中心开放课题基金资助项目(LSDP202101)
作者简介:唐晓宇,女,硕士研究生,主要从事岩土工程方面的研究工作。E-mail:1048531671@qq.com
通信作者:黄诗渊,男,讲师,博士,主要从事岩土体工程断裂相关研究工作。E-mail:cqjtdxhsy@163.com
