重构外Steklov特征值的交互间隙法
2023-07-21丘文松
丘文松 , 李 媛 ,2
(1.黑龙江大学 数学科学学院, 哈尔滨 150080;2.黑龙江大学 黑龙江省复杂系统与计算重点实验室, 哈尔滨 150080)
0 引 言
近年来,反散射领域中的一个热点问题是研究关于人工参数的特征值[1-10]。与传统的由物理波数充当特征值[11-12]相比,采用人工参数作为特征值有两个优势:一是重构这些特征值时无需使用多频数据,物理波数可以始终固定且为实值;二是这些特征值(包括复特征值)能够由测量的散射数据决定。由于这些特征值携带散射体的本质信息,因此可以作为目标特征用于无损探测领域,在应用方面具有极大的潜在价值。
外Steklov特征值是含有腔体的介质反散射中出现的一类关于人工参数的特征值,其相关的数学理论由文献[7]给出。同时,该文献采用了推广的线性抽样法[13]来重构这类特征值,测量的散射场数据和入射点源位于腔体内的同一流形上。文献[7]中的数值实验表明,外Steklov特征值的改变可以表征介质参数的变化。因此,为了使这类特征值能够作为目标特征应用于介质的无损探测领域,构造具有高精度和稳定性的重构特征值的算法至关重要。
本文采用交互间隙法(Reciprocity gap method)来重构外Steklov特征值[14],测量的总场的Cauchy数据和入射点源位于腔体内的不同流形上。交互间隙法已被应用至一系列反散射问题的研究中[15-21],其优点是无需散射体的任何先验信息,也无需构造背景介质的Green函数。本文的主要思想来源于文献[22]利用交互间隙法重构内Steklov特征值,而本文将重构外Steklov特征值。
1 正散射问题和外Steklov特征值问题
设D⊂d(d=2, 3)为包含原点的单连通有界Lipschitz区域,ν为其边界∂D上的单位外法向量。D1为d上包含D的有界Lipschitz区域,n∈L∞(d)满足条件:(i) 在D及内n=1; (ii) 在内几乎处处有Re(n)≥n*>0,Im(n)≥0,其中n*为常数。
(1)
式中:k>0为波数;ui=Φ(·,x0)表示位于x0处的点源;Φ(·,x0)为Helmholtz方程在d中的基本解;x为各函数的自变量。在前述关于n的假设下,问题(1)是适定的[23]。
设B和C均为d中的光滑区域,满足C⊂B⊂D,其中B包含原点。在每个x0∈∂C处放置点源,并在∂B上测量对应的总场的Cauchy数据u(x,x0)和∂νu(x,x0),这里
u(·,x0)=ui+us(·,x0),x∈D{x0}
(2)
假设1假设k2不是-Δ在C内的Dirichlet特征值。
外Steklov特征值问题可描述为[7]:寻找λ∈和一个非平凡的函数使得
(3)
称λ为一个外Steklov特征值,w为相应的特征函数。由文献[7]可知,问题(3)的外Steklov特征值若存在,将构成下半复平面上的一个离散集。

(4)
式中λ∈;x0∈∂C;ν为∂B上的单位外法向量。从文献[7]知,若λ不是实数,则问题(4)是适定的。由于所研究的目标是重构外Steklov特征值,故以下总假设Im(λ)<0,因此问题(4)是适定的。为了后面的使用,记为
(5)
2 交互间隙法
设U和Uλ分别为问题(1)~(2)的解u(x,x0)和问题(4)~(5)的解uλ(x,x0)构成的解集。定义交互间隙泛函为
其中v1在B{x0}(对所有的x0∈∂C)内满足Δv+k2v=0,v2∈H(这里,H(
定义单层位势
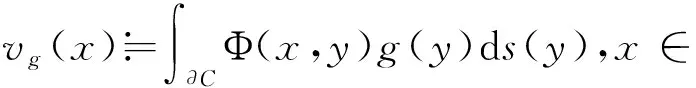
且令
交互间隙法是求积分方程
R(uλ(·,x0)-u(·,x0),vg(·))=R(uλ(·,x0),Φz(·)), ∀x0∈∂C
(6)
的近似解g∈L2(∂C),其中Φz(·)=Φ(·,z),z∈
引理1假设Im(λ)<0。若对于所有的uλ∈Uλ,有
则在∂B上f=0。

(7)
由于Im(λ)<0,则问题(7)是适定的。利用Green表示定理、Green第二公式和uλ满足的边界条件,有
=0, ∀x0∈∂C

定义算子N:L2(∂C)→L2(∂C)为
Ng:=R(uλ(·,x0)-u(·,x0),vg(·)),x0∈∂C
(8)
定理1假设Im(λ)<0。若λ不是问题(3)的一个外Steklov特征值,则由式(8)定义的算子N是单射。
证明假设对所有的x0∈∂C,有Ng=0,且(ps,p)满足
Δps+k2ps=0,x∈DΔp+k2np=0,x∈
p-ps=vg,x∈∂D
∂νp-∂νps=∂νvg,x∈∂D
(9)
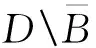
(10)
式中BR是d中以原点为中心,R为半径的球体,且BR严格包含D1。由于w和p均为Helmholtz方程在内的辐射解,故当R→∞时,式(10)中∂BR上的积分趋于0,从而
(11)
此外,由Green第二公式可知,
(12)
利用式(11)、式(12)以及uλ在∂B上满足的边界条件,有
=R(uλ-u,vg)
=0
(13)
延拓ps至上,使得ps=p-vg,则由问题(9)、式(13)和引理1可知,满足
因为λ不是问题(3)的一个外Steklov特征值,故在内ps+vg=0。由问题(9)和唯一延拓原则可知,在内ps+vg=0。根据迹定理和单层位势的连续性知,在∂C上ps+vg=0。由假设1,在C内ps+vg=0。因此,在∂C上,(∂νps)+=-(∂νvg)+, (∂νps)-=-(∂νvg)-
下面给出利用测量的总场的Cauchy数据重构外Steklov特征值的主要定理。
定理2假设Im(λ)<0,则如下结论成立:
(1) 若λ不是问题(3)的一个外Steklov特征值,则对任意的z∈都存在序列{gn}⊂L2(∂C),使得
(14)
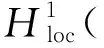
(2) 若λ是问题(3)的一个外Steklov特征值,则对每个满足
(15)
的序列{gn}⊂L2(∂C)和几乎每个z∈都有∞。
证明首先证明(i)。因为λ不是问题(3)的一个外Steklov特征值,则设wz是
Δwz+k2nwz=0,x∈
∂νwz+λwz=∂νΦ(·,z)+λΦ(·,z),x∈∂B
(16)
的解,其中z∈仍设BR是d中以原点为中心、充分大的R为半径且严格包含D1的球体。由Green表示定理,有
由于wz(·)和Φ(x,·)均为Helmholtz方程在内的辐射解,在上式中令R→∞,则有
(17)
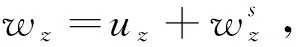
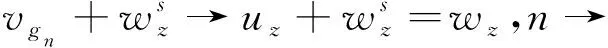
(18)
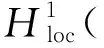
(19)
再利用式(18)及与得到式(11)类似的讨论可得
(20)
从式(18)~式(20)及wz满足的边界条件,有

(21)
设(h,hs)为
(22)
的解。由于vi在内满足Helmholtz方程,则采用与定理1中得到式(11)和式(12)类似的讨论,可得
(23)
和
(24)
结合式(21)、式(23)和式(24)以及uλ在∂B上满足的边界条件,有

由引理1,有
∂ν(hs+vi-Φz)+λ(hs+vi-Φz)=0,x∈∂B
(25)
记
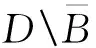

定义
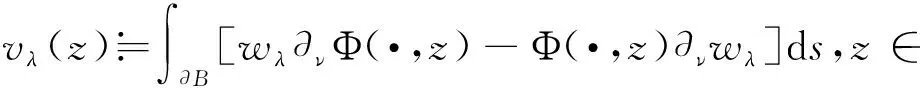
则在Bρ内vλ=0。根据唯一延拓原则,在内vλ=0。再定义
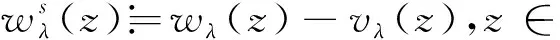
则从单层位势的跳跃关系知,在∂B上,

3 数值实验
由于问题(3)是非自伴的特征值问题,其特征值在一般情况下的存在性目前还是公开问题[7]。为了检验交互间隙法重构特征值的有效性,针对外Steklov特征值存在的一种情形给出数值算例。
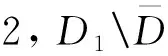
在∂C上100个等距分布的点处轮流放置点源,对于每个点源,在100个等距分布在∂B上的节点处计算总场的Cauchy数据,并采用带噪声的Cauchy数据进行反演,噪声水平为ε。利用分离变量法求解正散射问题(1)和辅助问题(4)。尽管外Steklov特征值都位于下半复平面上,但为了观测到某些靠近实轴的特征值,选取的抽样域将覆盖实轴上方较窄的带型域。具体地,选取抽样域为[1,4.4]×[-2.2,0.2],网格剖分步长取为0.1。针对抽样域内的每个抽样点λ和每个z∈(R0,10R0)(理论上z∈即可,但从数值实现的角度,z需取自外的有界域内,这里R0为∂B的半径),利用Tikhonov正则化和Morozov偏差原则求解积分方程(6)的离散形式,得到方程的近似解gλ的度量||gλ||l2,方程(6)中的所有积分都通过矩形公式进行离散。事实上,对每个抽样点λ都随机选取5个z,将对应的5个||gλ||l2的平均值作为最终的示性函数,仍记为||gλ||l2。通过作出||gλ||l2关于λ的图像,图像上的峰值点在抽样域上的投影即可被认为是外Steklov特征值的近似。
从外Steklov特征值的解析表达式可以算出,选定的抽样域中含有四个精确的特征值(见表1的第二行),分别对应于m=0,1,2,3,这里的m表示对应的特征函数在上的限制为m阶第一类Hankel函数。图1和图2分别给出了噪声水平ε=5%和ε=2%时的特征值重构结果,其中白色的星号代表精确特征值的位置,各等高线簇的中心(即示性函数的极值点)代表重构的特征值。可以看出,当ε=5%时,能够清晰地确定m=0, 1时的两个特征值,但几乎无法确定另外两个特征值。当噪声水平降至2%时,可以同时观测到四个特征值,见表1的第三行。因为抽样网格的步长是0.1,因此重构的特征值只能取到小数点后1位。这说明所采用的方法可以很好的重构出给定抽样域内的特征值。
表1 m取不同值时精确的和重构的特征值,m表示对应的特征函数在上的限制为m阶第一类Hankel函数
Table 1 Exact and reconstructed eigenvalues for different values of m, where m is the order of Hankel function of the first kind as the corresponding eigenfunction refined in

表1 m取不同值时精确的和重构的特征值,m表示对应的特征函数在上的限制为m阶第一类Hankel函数
m0123精确的特征值1.267 7-1.785 2i1.286 8-1.499 2i2.202 2-0.294 4i4.034 6-0.006 9i重构的特征值1.3-1.8i1.3-1.5i2.2-0.3i4.0-0.0i
由于在数值实验中使用的噪声数据是随机生成的,多次测试下的等高线形状会存在一些差异,但基本不会影响到与m=0,1,2对应的三个特征值。在某些次的测试中,对应于m=3的特征值可能会被重构为 4.1-0.0i,考虑到网格步长的选取,这种偏差是可以接受的。总之,与文献[7]相比,为了同时观测到给定抽样域内的几个特征值,本方法无需噪声水平低至千分点甚至万分点,显然对实际测量中噪声出现的环境要求更宽松。一个合理的解释是所采用的已知数据是总场的Cauchy数据,而文献[7]中采用的是散射场的数据,数据信息的增加可能弥补更大的噪声对重构结果的影响。
4 结 论
给出了由总场的Cauchy数据来重构外Steklov特征值的交互间隙法,基于一个含有交互间隙泛函的线性积分方程,用于反演的测量数据和入射点源位于腔体内的不同流形上。给出了该方法的理论分析,尤其是建立了积分方程近似解的爆破性质和外Steklov特征值之间的联系。数值算例表明,在给定的抽样区域内,利用该方法能够比较准确的重构出几个外Steklov特征值,但所能重构出的特征值数目与测量数据的噪声水平有关。在后续的研究中,将考虑利用交互间隙法重构其他类型的关于人工参数的特征值,如修正的外Steklov特征值等。此外,还将针对已经确定有存在性结论的特征值类型,在数值上考虑腔体和介质的几何形状以及介质参数(特别是吸收介质情形)等因素对重构效果的影响。
