基于流固耦合的橡胶坝平衡状态分析
2023-07-20张海涛
张海涛
(临沂市水利工程处,山东 临沂 276000)
0 引 言
橡胶坝因其结构简单,运行管理方便,抗震性能和生态景观好,常用于灌溉、防洪、挡潮等水利工程,但由于橡胶坝在运行中形状不断变化,主体材料为弹性材料,其结构和水力分析相较于刚性坝更为复杂,亟需对其运行安全影响因素进行分析。故此,对橡胶坝进行数值分析,以确定此类坝的平衡形状。假设溢流以均匀深度和速度开始。其中包括非线性自由表面流和结构响应,故使用ANSYS流固耦合模块并选择混合欧拉拉格朗日公式进行流体流动的非线性计算,研究内部压力、外部水头和流速对橡胶坝平衡形状的影响,并将结果与实际运行状态进行了比较,流体动力学程序确定自由表面高程,并计算在每个时间步长中作用在坝面上的外部压力。同时,将该压力作为每个时间步长的输入,以确定沿坝面的变形和速度以及坝内的应力[1]。结构应力计算结果被用于下一个时间步,以继续进行流体动力学分析。自由表面的数据被转换为随结构移动的坐标系,以显示自由表面如何随时间发展。在综合量纲分析中获得了流体-结构相互作用的重要参数,从而使橡胶坝的流量系数具有更精确的相关性,用于为类似项目提供理论依据。
1 工程概况
枣庄市蟠龙河综合整治工程山家林橡胶坝项目位于蟠龙河山家林湖的下游,蟠龙河南支入口下游,其橡胶坝处于长白山路交通桥上游约585m 桩号3+600 处。橡胶坝段包括坝袋、锚固系统、底板、边墩及中墩,坝段长16.0m,坝高5.0m,闸底板顶高程为46.100m,挡水位为51.00m,挡水高度5.00m,如图1 所示。橡胶坝总设计2 孔,为保证2 孔坝袋的水压平衡和坝袋安全,在中墩处设平压连通管和溢流管,溢流管与连通管连接,溢流管出口高程满足坝袋内压比的要求。
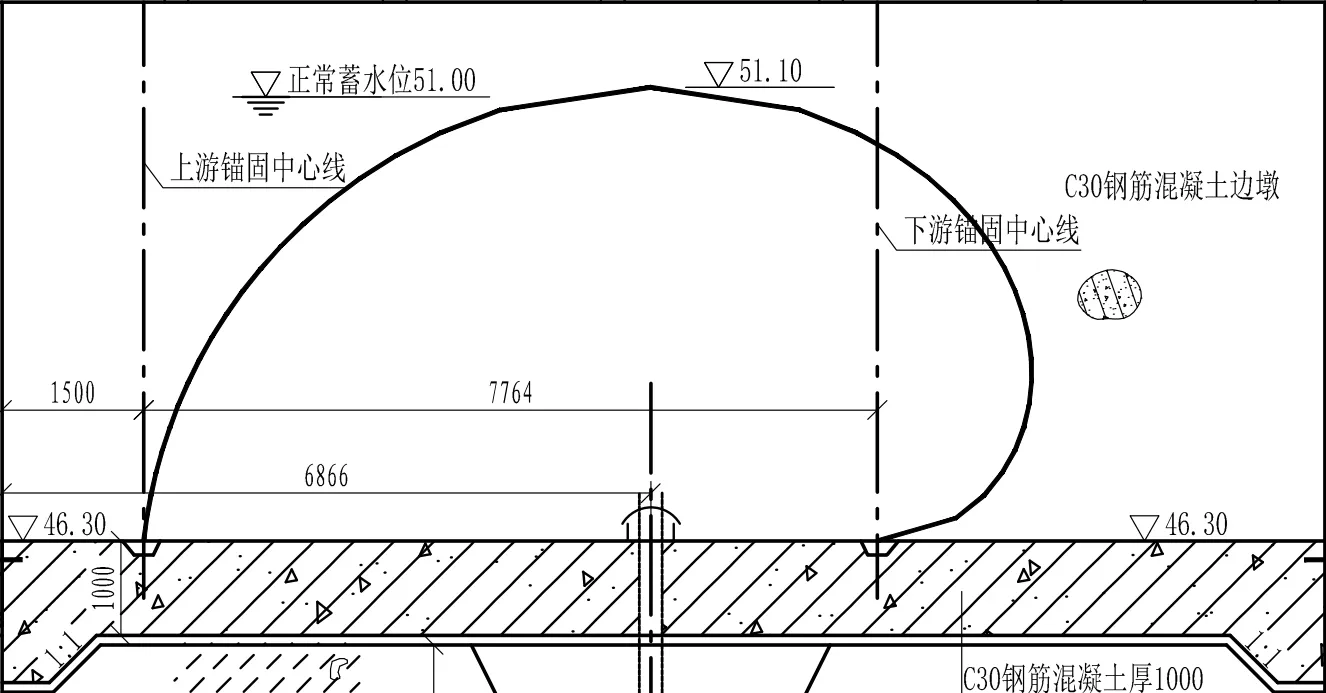
图1 橡胶坝示意图
2 量纲分析
基于一般堰顶流量公式:
橡胶坝运行最具体的参数包括相对于坝顶水位的上游水头、大坝平衡高度Dh、大坝的底宽B、重力加速度g、内部压力P、橡胶弹性模量E和橡胶厚度t,重要的流体参数是密度ρ、表面张力σ和动态黏度μ如图2 所示。因此,橡胶坝的具体流量取决于下列公式:

图2 橡胶坝数学模型
式中:f表示一个函数。应用量纲分析和不完全自相似性程序,等式(2)被重写如下:
式中:B*=B/(D/2),P*=P/γHu,E*=Et/[γ(D/2)2],D=2P/π为初始橡胶坝的等效直径,γ为水的重度,W和R分别为韦伯数和雷诺数,当上下游水头差>3m 时,韦伯数可以忽略不计。此外,此工程的流动是湍流,黏度效应要远小于重力效应,所以雷诺数也忽略不计[2]。
因此,必须将其他无量纲参数的影响插入到橡胶坝的平衡高度中,如下式:
3 数值模拟
使用ANSYS建立橡胶坝的三维数值模型,使用ANSYS CFD流固耦合模块解决静态和动态结构分析的问题。在瞬态结构分析系统中建立了结构物理,在流体流动(CFD)分析系统中建立了流体物理。目的是确定橡胶坝在流固耦合作用下的平衡状态[2-4]。
作用在橡胶坝的力包括内部压力和外部水压。大坝本身的重量与其他的力相比可以忽略不计,与地基的摩擦也被忽略。受力假设为允许预测大的非定常运动和大坝的小偏转,并假设溢流以均匀接近的流深和速度开始。边界条件为固定两点上锚定在底部。大坝具有均匀的厚度和恒定的弹性模量。橡胶坝的尺寸和材料性能是根据的实际情况来选取。下游垂直边界采用开放边界条件,模拟流体流动。
主要存在以下两个问题;非线性自由表面流和结构变形。由于结构变形影响流体,而流体影响结构变形,因此需要两种分析之间的耦合来模拟结构体系和流体体系之间的相互作用。流体流动依赖于结构变形,而结构变形依赖于流体力。使用混合欧拉-拉格朗日公式对流体流动进行了瞬态的、完全非线性的计算。考虑了外部静止静态和溢流条件下橡胶坝的平衡形状和内部压力。流体动力学程序确定自由表面高程,并使用多相流模型(VOF)方法计算在每个时间步长中作用于坝面的外部压力[5]。然后,将该压力作为每个时间步长的输入,以确定沿坝面的变形和速度。CFD 在下一步中使用这些信息继续流体结构相互作用分析。然后将该结构的变形应用于流体边界条件下。关于自由水表面的响应的数据被转换为一个随结构移动的坐标系,以显示自由水表面是如何随时间发展的。这个过程一直持续到稳定的自由水面和结构的平衡形状形成。
流体模型中的网格生成直接由CFD-Mesh 自由创建,其中速度梯度较高的区域,流体与结构之间的界面和无水表面划分较细的网格。
通过数值分析计算了橡胶坝模型中心的顶高和横截面积。并与实际测量数据进行了比较。通过比较结果,得出在相同条件下,结构的模态形状、平衡形状和坝体高度与实际测量结果非常一致,如图3 所示。变形橡胶坝轮廓的些许差异考虑是数值分析中的网格尺寸和测量误差。除了数值误差和测量误差外,实际中坝两端与地面之间产生的摩擦力的影响,进一步扩大了误差。综上,数值模拟的结果基本可信。
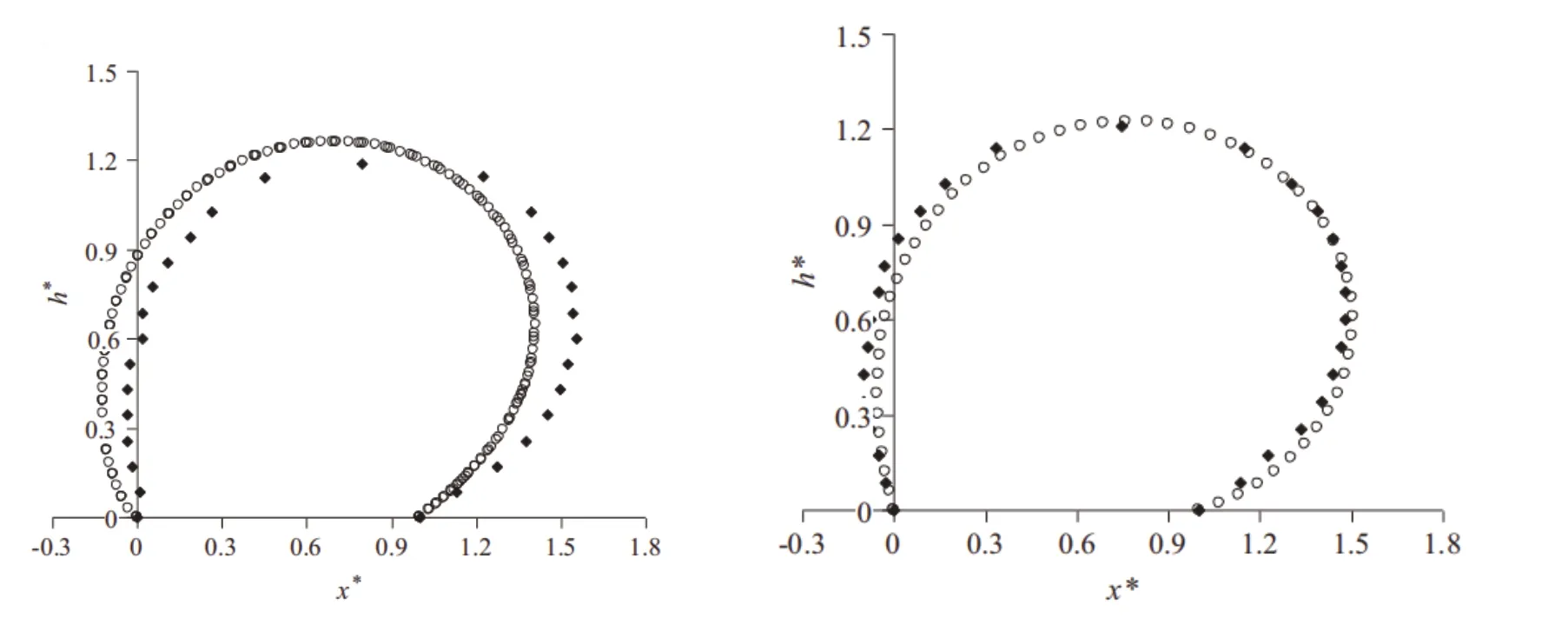
图3 流量为19.9L/s 和9.5L/s 时橡胶坝的平衡状态
进一步分析了内压、上游水头、膜厚度和弹性模量以及自由形状直径和底宽条件下橡胶坝的性能。根据不同的变量,建立了以下五组数值模拟。
橡胶坝的结构性能受到内外压力的影响。在内部压力下,橡胶坝开始逐渐直立,橡胶坝的形状和横截面发生变化。图4 示出了增加内部压力对橡胶坝的横截面形状的影响。内部压力从1.5 kPa 变为5.0 kPa,同时保持上下游水位差不变。在该图中,h*和x*分别为相对水深和纵向位移。如图所示,内部压力较低时发生大变形。随着内压的增加,坝高增加。对于较小的内压值,横截面朝下游偏转,成为泪滴形橡胶坝而不接触大坝底部,而对于较高的内压值,最终形状为椭圆形。有限元模型的输出与图1 基本一致。当内压值增加到一定程度时,结构的高度基本不变,并且上游位移与内压值关联性较大,下游位移基本与内压值无关。
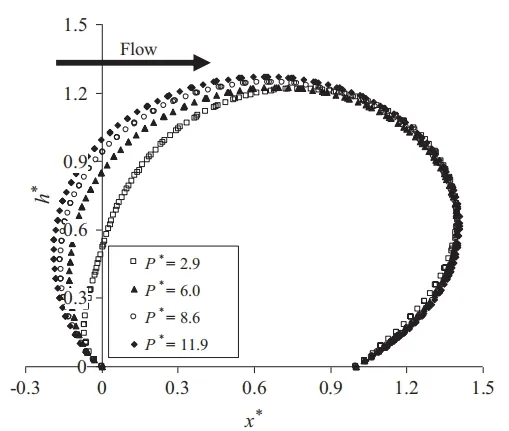
图4 不同内压值下橡胶坝的平衡状态
进一步研究了上游水头对橡胶坝行为的影响,如图5 所示。在内压不变的情况,橡胶坝随着上游水头的增大而较少,坝体的平衡形状向下游倾斜,呈现泪滴状。在实际运行情况中橡胶坝上游坡度随着上游水头的增加而减小,表示其向下游方向变形,与模拟结果相似。

图5 不同水头差下橡胶坝的平衡状态
通过改变橡胶坝底宽B 来研究其对橡胶坝的高度的影响。如图6 所示,底宽的降低导致了橡胶坝平衡高度的增加。随着底宽的降低,橡胶坝逐渐向下游倾斜并最终形成螺旋平衡形状。当底宽较大时,会逐渐形成椭圆形。
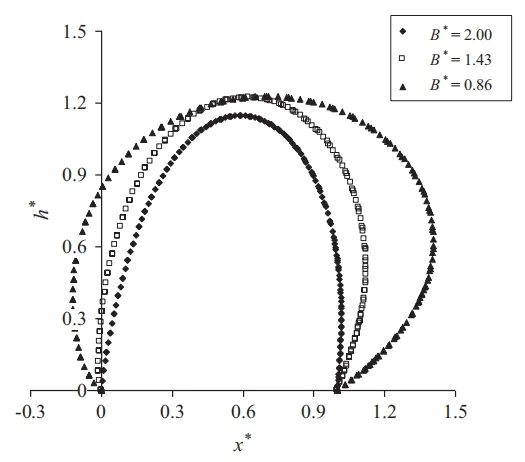
图6 不同坝底宽下橡胶坝的平衡状态
利用无量纲参数E*研究了膜厚度和弹性模量的变化对大坝最终高度和平衡形状的影响如图7 所示。随着E*的增大(增加弹性模量或厚度),橡胶坝高度随之减小,最终呈椭圆形,而E*的减少导致橡胶坝平衡高度增加,橡胶向下游倾斜,形成泪滴形。不同E*下橡胶坝的平衡状态,见图7;三维橡胶坝水平位移,见图8。
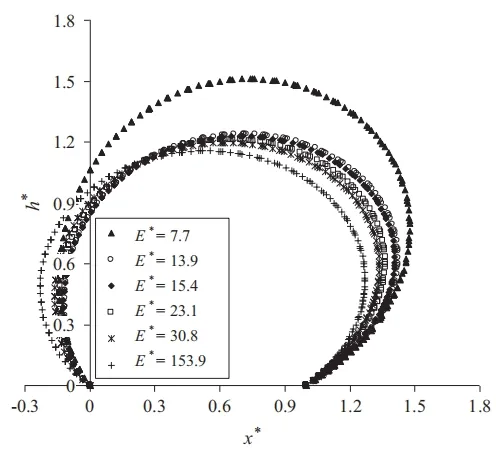
图7 不同E*下橡胶坝的平衡状态

图8 三维橡胶坝水平位移
溢流条件下的橡胶坝样本位移曲线,如图8 所示。
分析表明,初始状态溢流将大坝推向下游,随后大坝来回振荡,振荡的幅度取决于内部压力的大小。随着时间的推移,坝前水高达到稳定值。这个高度取决于溢流的深度和速度。随着流动的稳定,振荡的幅度减小,直至消失。这种振荡对橡胶坝的运行极为不利,会导致溢流只从中间位移较大的部位流出,形成V 型缺口,这可能导致坝体结构振动、流量变化和橡胶坝基础失效。
综上,所有参数对山家林橡胶坝进行了结构优化,满足防洪、蓄水、除涝、灌溉等功能要求,也满足了结构的安全性和稳定性。
4 结 论
利用ANSYS 软件研究橡胶坝在固定静水和溢流条件下行为,对橡胶坝几种结构特性和水力特性进行数值分析,成功地模拟了橡胶坝的平衡形状和高度。实际测量结果与数值模拟结果有很好的一致性。数值结果表明,橡胶坝在高内压条件下的横截面积为半圆型,此时橡胶坝的泄洪系数增大。同时,随着外部压力的增大、橡胶坝底宽的增大、橡胶弹性模量和厚度的增大、上游水头的增大,橡胶坝会逐渐向下游倾斜并最终呈泪滴状,并根据水平位移云图对橡胶坝形状进行优化,保证了其安全运行。
