无人机级联中继广播通信系统航迹优化方法
2023-07-19李冬霞宋思雨刘海涛
李冬霞, 宋思雨, 刘海涛
(中国民航大学 天津市智能信号与图像处理重点实验室, 天津 300300)
无人机(unmanned aerial vehicle,UAV)中继通信可以有效扩大通信覆盖范围,克服信道衰落和路径损耗,保证通信的可靠性[1];且UAV具有组网灵活、部署快速、运行成本低等优点,已成为无线中继通信的重要方式[2]。由多UAV组成的机群协作部署和传输,能够克服单UAV在载荷能力、续航时间、功率等方面的制约,更好保证信息传输的可靠性、高效性和稳定性。多无人机协作传输的无线中继通信系统将会成为未来无线通信的一个重要组成部分。
近年来,围绕UAV动态中继之间的协作问题,已开展航迹优化[3-9]、资源分配[10]和网络优化[11]等多方面的研究。本文将围绕无人机航迹优化方法进行相关研究。针对点对点UAV级联中继通信系统航迹优化问题,文献[3]基于端到端信噪比最大化准则,比较了译码转发(decode-and-forward,DF)和放大转发(amplify-and-forward,AF)2种转发协议下系统的中断概率和误码率。文献[4]对于有缓存和无缓存的多跳中继网络,给出了在传输功率较大区域内的渐近中断概率和误码率,并验证了缓存的使用可以为UAV系统提供可靠和低延迟的通信。文献[5]基于通信链路遍历容量最大化准则提出UAV航迹优化方法。文献[6]提出一种利用人工势场法以系统容量最大化为优化准则的UAV航迹优化方法,但没有研究信道衰落对系统性能的影响。文献[3-6]在系统建模中只考虑了单个用户,没有考虑多UAV在多用户情况下的航迹优化问题。然而,对于UAV中继通信系统的研究,多用户场景的广播通信比单用户场景更具有现实意义。
针对UAV中继广播通信系统航迹优化的研究,目前主要面向单UAV中继广播通信系统。如文献[7]基于公平吞吐量最大化准则,提出了旋翼UAV航迹优化方法,但该系统只分析了UAV和用户之间的链路,没有研究基站到UAV之间的链路对系统的影响。文献[8]基于各链路加权和遍历容量最大化准则提出了UAV航迹优化方法。文献[9]以平均中断概率最小化为准则对UAV进行航迹优化,并定量分析了无人机的系统性能。当前对于多UAV协作传输的广播通信系统的航迹优化方法及其对系统整体性能的研究很少见诸于公开文献资料。
本文研究了UAV级联中继在静态用户广播通信系统中的航迹优化问题,在DF协议下基于最大用户中断概率最小化准则给出了联合优化和分步优化2种UAV航迹优化方法,推导出用户链路中断概率和系统容量表达式,最后通过计算机仿真验证了所提航迹优化方法的正确性。
1 UAV级联中继广播通信系统
1.1 系统模型
图1为无人机级联中继广播通信系统示意图。系统由固定地面基站(base station,BS)、2架固定翼无人机(分别记为UAV1和UAV2)及N个用户Ui(i=1,…,N)节点等四部分组成,其中N个用户节点分布在地面圆形服务区内。假设BS与用户Ui节点之间有较远的通信距离,无法进行直接通信,需要借助2架中继UAV级联实现BS到用户节点的通信。此外,所有通信节点均为单天线,且2架UAV均采用DF协议进行中继通信。

图1 无人机级联中继广播通信系统示意图
1.2 信号模型
BS节点发送的信号通过3个时隙传输到用户节点。在第一个时隙,BS节点发送信号至UAV1,则UAV1接收信号为

(1)

在第二个时隙,UAV1将接收到的信号解码处理,重新编码后发送给UAV2,则UAV2接收信号为
(2)

在第3个时隙,UAV2将接收到的信号通过解码、编码,广播发送至用户节点Ui(i=1,…,N),则用户Ui节点接收信号为
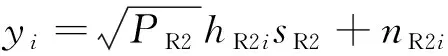
(3)

1.3 UAV1、UAV2与用户节点的输入瞬时信噪比
BS~UAV1、UAV1~UAV2、UAV2~用户Ui节点链路之间为瑞利衰落信道,建模为

(4)
式中:dβ为各节点之间的距离;α为信道的损耗因子;gβ~CN(0,1)为信道小尺度衰落系数。
根据(1)~(4)式,可以得到UAV1、UAV2和用户Ui节点的瞬时信噪比分别为
(5)
(6)
(7)

(5)~(7)式表明:γR1通过距离dBR1和信道的小尺度衰落系数gBR1联合确定;γR2通过距离dR1R2和信道的小尺度衰落系数gR1R2联合确定;γi通过距离dR2i和信道的小尺度衰落系数gR2i联合确定。
2 中继UAV级联航迹优化方法
在UAV级联中继广播通信系统中,实时优化UAV1和UAV2的航迹,以获取最佳的通信性能。本文基于最大用户中断概率最小化准则给出UAV级联中继的联合优化方法和分步优化方法的航迹优化方法。联合优化方法是同时优化UAV1和UAV2的航向角,分步优化方法是先优化UAV1的航向角,然后再优化UAV2的航向角。
2.1 用户中断概率
图1所示级联UAV系统中用户Ui节点的中断概率为
(8)
式中:PBR1,PR1R2与PR2i分别为BS~UAV1、UAV1~UAV2和UAV2~用户Ui节点链路的中断概率。由于PBR1,PR1R2和PR2i取值较低,(8)式近似为[9]
PUi≈PBR1+PR1R2+PR2i
(9)
利用(5)~(7)式,可计算得到用户Ui节点的近似中断概率为
(10)
将(10)式进行泰勒展开,取第一项代入(10)式,则用户节点的中断概率化简为
(11)
(11)式表明:影响用户Ui节点中断概率的主要因素为各节点之间的距离(dBR1,dR1R2,dR2i)。
2.2 联合优化方法
为了定量分析,建立三维直角坐标系如图1所示,计算各节点之间距离,假设t时刻BS、UAV和用户Ui节点的坐标矢量分别为b=[xb,yb,0]T,rRm,t=[xRm,t,xRm,t,hRm,t]T(m=1,2)和ui=[xi,yi,0]T。假设UAV中继在t-Δτ时刻的位置坐标为rRm,t-Δτ=[xRm,t-Δτ,xRm,t-Δτ,hRm,t-Δτ]T(m=1,2),根据固定翼UAV的运动模型,其在t时刻的坐标可表示为[12]
(12)
式中,υRm为UAV的飞行速度;Δτ为中继位置更新的时间间隔;δRm,t为t时刻中继UAV的航向角,且|δRm,t-δRm,t-Δτ|≤δmax,δmax表示最大转弯角,这里假设UAV1和UAV2的最大转弯角相同。结合(12)式,dBR1,dR1R2与dR2i可以分别表示为
(13)
dR1R2,t=

(14)
(15)
(12)~(15)式表明:t时刻用户Ui节点的中断概率只取决于UAV的航向角δRm,t。
为了使t时刻级联UAV中继广播通信系统性能最优,基于最大用户中断概率最小化准则优化UAV的航向角[13],则上述优化问题表示为
(16)
(16)式中的优化问题可以进一步表示为[14]
(17)
其中p大于零,(17)式中的优化问题是含有约束条件的二维非线性优化问题,该问题可以通过二维搜索算法在[δRm,t-Δτ-δmax≤δRm,t≤δRm,t-Δτ+δmax]内找到最佳航向角。
2.3 分步优化方法
2.3.1 UAV1航迹优化问题
在无人机级联中继广播通信系统中,在单个位置更新间隔内,无人机的空间位置改变量较小,因此在优化UAV1的航向角时,可近似认为UAV2空间位置没有产生变化,此时仅需要对BS~UAV1~UAV2链路来优化UAV1的航向角δR1,t;再以优化得到的δR1,t为基础,针对BS~UAV1~UAV2~用户节点Ui链路来优化UAV2的航向角δR2,t。
由(5)~(6)式可以得到t时刻BS~UAV1~UAV2链路的中断概率为
(18)
考虑到在位置更新的时间间隔内,UAV2的移动距离相对较小,因此,dR1R2由t时刻UAV1的位置坐标rR1,t和t-Δτ时刻UAV2的位置坐标rR2,t-Δτ确定,即dR1R2可以表示为

(19)
式中
(13)~(14)和(19)式表明:在t-Δτ时刻UAV1的位置rR1,t-Δτ给定后,t时刻的dBR1,t和dR1R2,t仅由UAV1的航向角δR1,t决定,则t时刻BS~UAV1~UAV2链路的中断概率Pt仅取决δR1,t。因此,为使t时刻该链路的中断概率最小,基于BS~UAV1~UAV2链路中断概率最小化准则优化UAV1的航向角,该优化问题表示为
(20)
(20)式描述的优化问题是含约束条件的一维非线性优化问题,该问题可以通过一维搜索算法在[δR1,t-Δτ-δmax≤δR1,t≤δR1,t-Δτ+δmax]内找到最佳航向角。
2.3.2 UAV2航迹优化问题
当UAV1在t时刻的最佳航向角被确定后,级联UAV系统的中断概率仅由UAV2的航向角决定。为使系统中断概率最低,针对BS~UAV1~UAV2~用户Ui节点链路,以用户最大中断概率最小化为准则优化UAV2的航向角。因此,(17)式的优化问题可以等效为
(21)


(22)
式中
(22)式表明:在t-Δτ时刻UAV2的位置rR2,t-Δτ给定后,dR1R2,t和dR2i,t仅由t时刻UAV2航向角δR2,t决定,因此,(21)式的优化问题进一步等效为
(23)
(23)式的优化问题是一维约束的非线性优化问题,该问题通过一维搜索算法在[δR2,t-Δτ-δmax≤δR2,t≤δR2,t-Δτ+δmax]内找到最佳航向角。
2.4 算法复杂度分析
算法1 联合优化算法
1.输入:b,rRm,t(m=1,2),T=200 s、用户数N等所需参数,初始化BS、UAV1、UAV2的位置。
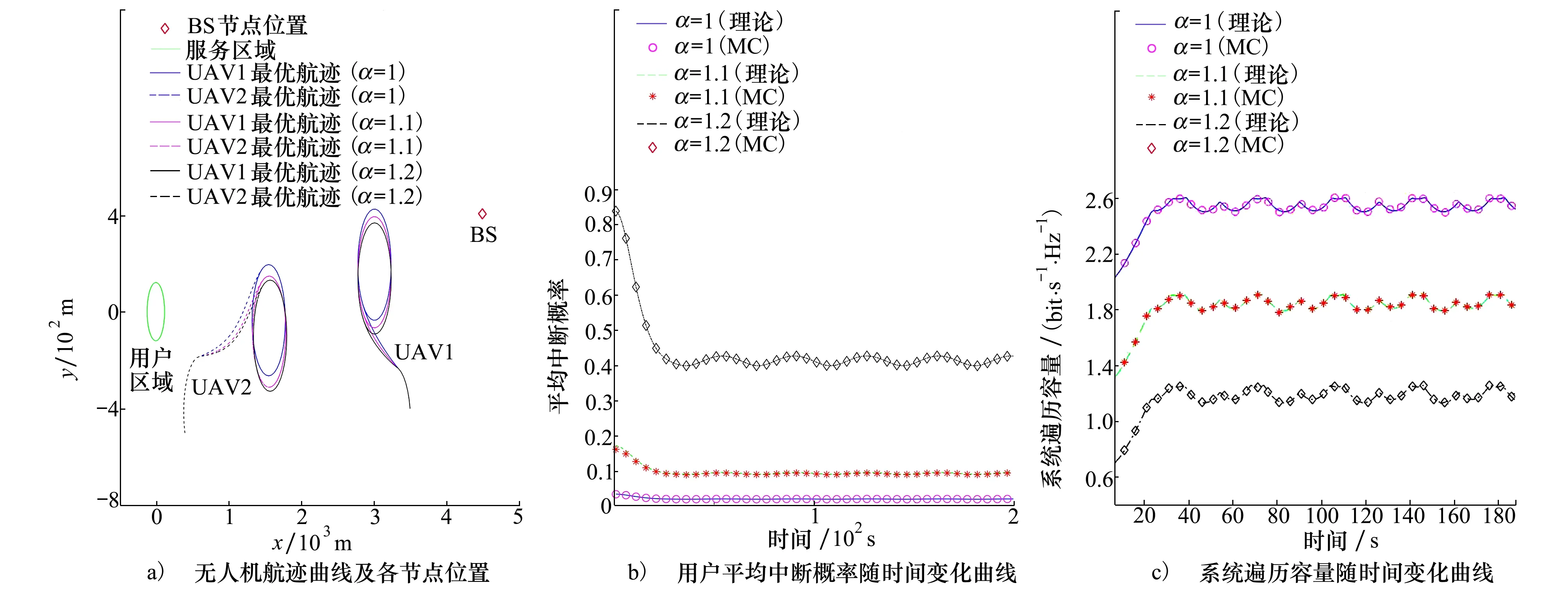
2.whilet 3.fori=1,2,…,Ndo 4.计算dBR1,t,dR1R2,t,dR2i,t,代入(11)式计算中断概率 5.end for 6. 确定UAV1航向角取值范围的长度Lδ1 7.确定UAV2航向角取值范围的长度Lδ2 8.fork=1:Lδ1do 9.fors=1:Lδ2do 10.用(13)~(15)式表示dBR1,t,dR1R2,t,dR2i,t,求解(17)式 11.end for 12.end for 14. 根据无人机运动方程实时优化无人机航迹 15. end while 16.输出:全局极值 根据(5)式,可得到BS~UAV1中继节点链路的瞬时容量为 (24) 根据(6)式, 可得到UAV1~UAV2中继节点链路的瞬时容量为 (25) 根据(7)式, 可得到UAV2~用户Ui节点链路的瞬时容量为 (26) 由(24)~(26)式可以得到,UAV级联中继广播通信系统第i条链路的各态历经性容量可以表示为 Ci=EgBR1,gR1R2,gR1i(min(CR1,CR2,CUi)) (27) 式中,E[·]代表均值。CR1,CR2和CUi分别是关于gBR1,gR1R2和gR2i的独立分布函数。(27)式可以进一步表示为 Ci=min(EgBR1(CR1),EgR1R2(CR2),EgR1i(CUi)) (28) 将(5)~(7)式代入(28)式,得到: (29) (30) 通过上述分析,UAV级联中继广播通信系统所有链路总的遍历容量(简称:系统遍历容量)为 (31) 图2显示UAV采用联合优化方法和分步优化方法分别得到的UAV最优航迹、用户平均中断概率及系统遍历容量。仿真结果说明:采用联合优化方法与分步优化方法所得到的UAV1和UAV2的最优航迹、用户平均中断概率和系统遍历容量曲线几乎重合,表明了所提方法的正确性。2种优化方法都是根据UAV运动模型将中断概率表示成含有航向角的表达式,利用最大用户中断概率最小化准则优化2架UAV的航向角,且仿真参数条件设置相同。所以联合优化与分步优化的性能几乎相同。 图2 联合优化与分步优化对比 图3显示联合优化方法下最大转弯角对UAV最优航迹和系统性能的影响。仿真结果说明:①随着最大转弯角增大,UAV圆形飞行轨迹的半径减小,约为蓝色圆形轨迹半径的1/2;②随最大转弯角的增大,用户平均中断概率减小,系统遍历容量增大,级联UAV系统性能提高,但无明显差别。 图3 最大转弯角对无人机最优航迹及系统性能的影响 图4显示联合优化方法下路径损耗因子对UAV最优航迹、用户平均中断概率和系统遍历容量的影响。仿真结果说明:①随着路径损耗因子增大,UAV飞行轨迹发生变化,但圆形飞行轨迹的半径保持不变;②路径损耗因子从1增大到1.1,用户平均中断概率提高约4.3倍,系统遍历容量减少约为27%,级联UAV系统的性能明显下降。 图4 路径损耗因子对无人机最优航迹及系统性能的影响 图5显示出了各节点发射功率与噪声功率的比值对UAV最优航迹、用户平均中断概率和系统遍历容量的影响。仿真结果表明:①随着发射功率与噪声功率比值的增大,UAV1飞行轨迹不变,UAV2飞行轨迹发生小的变化;②发射功率与噪声功率的比值对中继通信系统性能影响较大,该值从90 dB增加到95 dB时,用户平均中断概率减小约为68%,系统遍历容量提高约为1.2倍,级联UAV系统的性能明显提高。 图3~5所示的Monte-Carlo(MC)仿真曲线与理论仿真曲线变化规律基本一致,验证了本文推导的系统遍历容量和单个用户中断概率数学表达式的正确性。 针对UAV级联中继广播通信系统航迹优化问题,给出了联合优化方法和分步优化方法,并通过计算机仿真验证了所提方法的有效性。主要研究结论如下:①联合优化方法和分步优化方法得到的中断和容量性能无明显差别;②路径损耗因子和各节点发射功率与噪声功率的比值对系统的中断概率和遍历容量影响较大。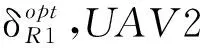

2.5 系统遍历容量



3 数值仿真
3.1 仿真参数
3.2 仿真结果


4 结 论
