多体飞行器展开过程动力学特性研究

王宇, 祝小平, 周洲

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.西北工业大学 航空学院, 陕西 西安 710072)

随着航空工业技术的发展,高空长航时飞行器成为科研工作者的研究焦点。空中发射技术的发展使高空长航时飞行器能够直接在平流层中水平发射起飞,从而使飞行器快速切入巡航状态。这种起飞方式减少了对流层的风场对此类飞行器的影响,同时减少了飞行器滑跑、起飞和爬升耗费的时间和能量。但高空长航时飞行器为了能够提高升阻比,往往采用大展弦比的布局形式,由于大展弦比飞行器的横向尺寸过大,不利于将其带到超高空或是临近空间,也不利于机库的存放,因此需要采用折叠翼技术来解决此类问题。

随着科技的发展,折叠技术越来越多地应用在飞行器上。因其结构简单、占用空间小等,在变体飞行器中得到了广泛的应用,例如美国的F/A-18和F-35C舰载机、俄罗斯的米格-29舰载机都采用了机翼折叠技术,有效缩小了机库存放空间,大大提高了舰上飞机的数量以及战斗能力[1]。在飞行器的储存、运输、空中投放与发射过程中,为了能够减小机体横向尺寸,通常改变机翼的结构设计,使其在展开过程中满足一定的力学性能。机翼的展开运动过程是飞行器飞行控制的关键因素。然而大幅度的变形必然会引起飞行器的转动惯量、重心位置以及焦点位置等一系列机体特性的改变,折叠型多体飞行器的气动力以及动力学特性也会随之变化,因此需要针对折叠型多体飞行器建立合适的动力学模型以及研究折叠型多体飞行器水平展开飞行过程中的动力学特性。

国内外对各种折叠型变体飞行器的动力学建模、仿真以及飞行试验等进行了理论及应用研究。薛臣[2]在折叠翼飞行器变形过程飞行控制研究中参考传统固定翼飞行器动力学模型,引入转动惯量对时间的导数并消除与纵向无关的状态量,建立了表征运动特性随着折叠参量变化的纵向线性变参数模型。在折叠翼飞行器的动力学模型的基础上设计了飞行控制器。乐挺等[3]在Z型翼变体飞机的纵向多体动力学特性中对机翼变形过程中的Z型翼变体飞行器进行了纵向多体动力学建模仿真,推导了变形过程中变体飞行器的六自由度非线性动力学方程,并通过简化得到了解耦后的纵向动力学方程。随着多体系统动力学理论的发展,采用多体系统动力学理论针对折叠型多体飞行器建立多刚体动力学模型的方法逐渐成为主流。Montalvo和Costello在Meta Aircraft Flight Dynamics中采用牛顿-欧拉法针对多体飞行器建立了多刚体动力学模型,对其非线性动力学进行了建模与仿真,研究了多体飞行器的飞行动态运动模式以及灵活运动模式,并得到了飞行器连接特性带来的影响[4-7],但其在建模时没有建立约束模型,而是将约束模型简化成接触力模型。高峰等[8]在仿生变形飞行器多体动力学建模与仿真中将仿生飞行器简化为五刚体模型,采用拟坐标形式的拉格朗日法并结合涡格法准定常气动力模型建立了仿生飞行器的动力学模型,通过数值仿真计算得到了变形运动规律,但该方法微分运算和推导过程繁琐且无法反映约束力。张杰等[9]在一种变体飞行器的动力学建模与动态特性分析中采用凯恩方法对变后掠伸缩折叠翼进行了动力学建模的研究,但该方法采用了惯性力矩和惯性加速度项,增加了方程推导的复杂性。

本文以折叠型多体飞行器为研究对象,该对象的特点在于可以将每个翼段看作是一个独立的飞行单元,飞行单元之间通过铰链进行连接并在铰接处添加卷曲弹簧,折叠型多体飞行器在平稳展开后仍能实现自由变形。该研究对象的特点决定了传统飞行器六自由度模型不再适用,需采用多体系统动力学理论进行建模。因此采用绝对坐标方法和变分方法,建立适用于折叠型多体飞行器的多体动力学模型。在非线性多体动力学模型的基础上,通过数值仿真计算,深入研究折叠型多体飞行器在水平发射后自由展开过程中的动力学特性。并进一步研究飞行单元之间柔性连接的刚度系数对多体飞行器动力学特性的影响以及连接刚度系数与最大初始折叠角之间的相互关系,从而确定连接刚度与最大初始折叠角之间的稳定域包线。

1 多体飞行器多刚体动力学模型

1.1 无约束刚体的动力学方程

以某折叠型三体飞行器为例(如图1所示),将折叠型三体飞行器简化为三刚体模型,该模型由3个翼段铰接而成,形成一个完整的无根树系统。模型建立时,忽略旋转铰的尺寸以及铰链间隙,刚体与刚体之间通过旋转铰约束。三体飞行器的多刚体系统的简化模型如图2所示。

图1 折叠型三体飞行器示意图

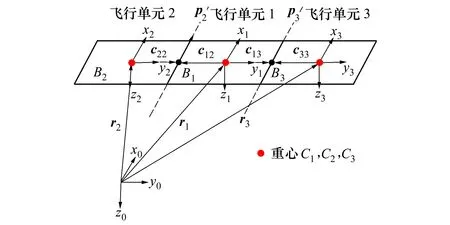
图2 折叠型多体飞行器多刚体系统简化模型

将每个刚体看作一个独立的飞行单元,Ci(i=1,2,3)为各个刚体的重心。解除所有铰对刚体的运动学约束,将铰的主动力视为对刚体施加的外力。利用牛顿-欧拉方程分别对各刚体建立动力学方程,从而导出各自独立的无约束刚体相对惯性坐标系的质心运动方程和绕质心转动的姿态运动方程,综合为

(1)

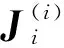
(2)

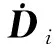
(3)

1.2 旋转铰约束模型

若刚体Bj及其内接刚体Bi(j)的铰为旋转铰,其第一个约束条件为Bj上的铰点与Bi(j)上的铰点重合为同一点Oj。

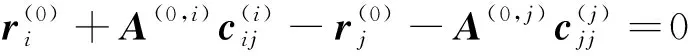
(4)

式中,cij和cjj为自Oci和Ocj出发至铰点Oj的体铰矢量。第二个约束条件单自由度旋转铰Oj约束的刚体进能够绕转轴基矢量pj转动。因此要求Bj与其内接刚体Bi(j)上的转轴基矢量重合为同一矢量pj,表达为

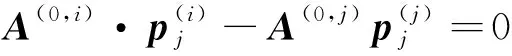
(5)

1.3 柔性连接模型

各飞行单元之间通过线性卷曲弹簧进行柔性连接,卷曲弹簧作用力矩的计算公式

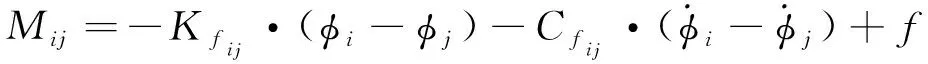
(6)

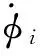
1.4 约束方程的加速度形式

Φk(q1,q2,…,q6n,t)=0(k=1,2,…,s)

(7)

将Φk按次序排列成s阶列阵并对时间t求导,得到

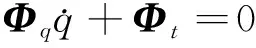
(8)

(8)式中s×6n阶矩阵Φq为Φ(q)的雅可比矩阵,Φt为s阶列阵,定义为

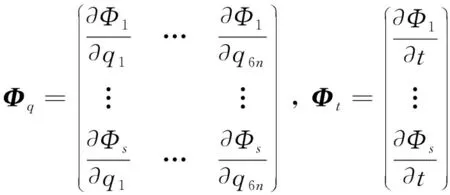
(9)

为了能够与动力学方程组联立求解,需要将(8)式再对时间t求导,得到加速度形式下的约束方程,简写为

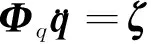
(10)

式中,s阶列阵ζ定义为

(11)

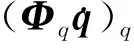
1.5 受约束系统的动力学方程

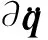
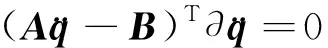
(12)

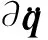
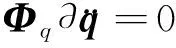
(13)

引入s个拉格朗日乘子λk(k=1,2,…,s),组成列阵λ。将(13)式表示的s个约束方程分别与相同标号的拉格朗日乘子相乘,再与动力学普遍方程(12)相加,得到

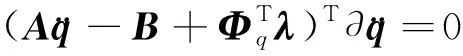
(14)

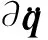
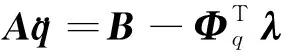
(15)

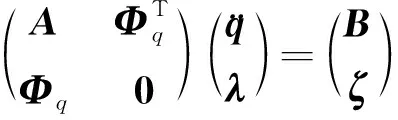
(16)

(16)式即为绝对坐标描述下的多体系统动力学方程组。

2 气动力模型

由于多体飞行器是由多个翼段通过铰链连接而成,各翼段之间会存在气动干扰,相关的文献、CFD数值仿真计算以及风洞模拟仿真试验[11]证明,当翼段与翼段相互接近时,翼尖之间的气动干扰使得各翼段的气动力产生强耦合效应而且连接间隙也会对耦合效应产生影响。因此,在建立折叠型多体飞行器的气动力模型时,主要采用CFD方法和升力线法[12]研究多体飞行器各翼段之间的耦合效应,同时忽略铰链间隙对多体飞行器各翼段气动力的影响,建立考虑气动耦合效应的数据库,再通过数据拟合得到多体飞行器各翼段的气动力模型。

基于定常RANS方法开展不同折叠角下的三翼段耦合气动特性分析。采用结构嵌套网格进行流场网格划分,背景网格远场取50倍机体长度,壁面第一层网格高度y+≈0.6,网格总规模946万。多体飞行器全机结构网格的划分如图3所示。物面和远场分别采用无滑移边界条件和压力远场边界条件。湍流模型应用SST模型,求解采用Roe隐格式,空间离散均为二阶精度。计算状态为高度H=0.5 km,速度V=10 m/s。将每个飞行单元看作一个独立的飞行器,通过CFD计算得到各自的气动力和气动力矩,再将气动力和气动力矩添加到相应的飞行单元重心位置上。

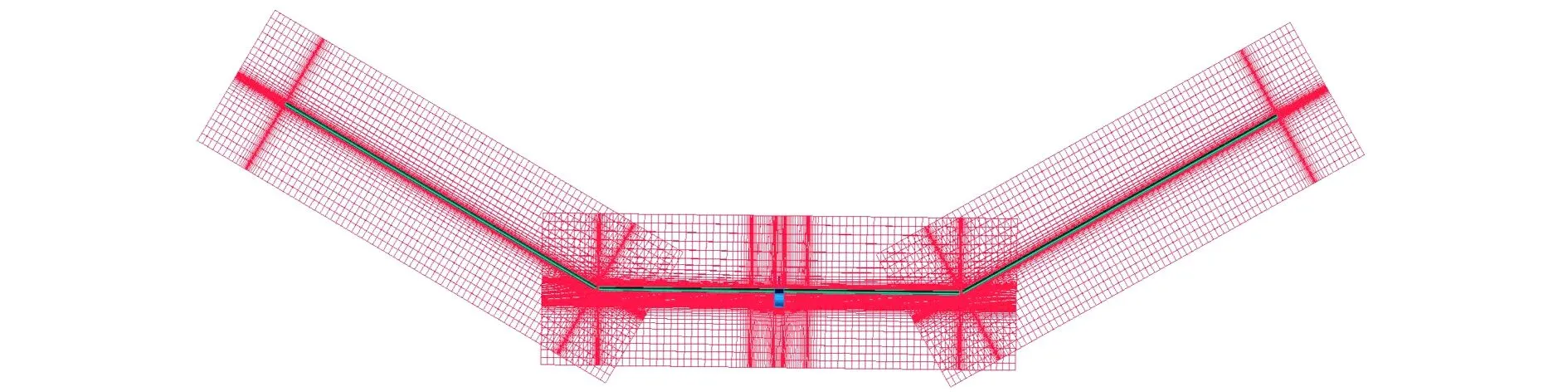
图3 折叠型多体飞行器系统结构网格划分

翼段翼尖与翼尖之间的气动耦合效应使得飞行单元1的气动力是对称分布,但是飞行单元2与飞行单元3的气动力并非对称分布,气动力的分布形式如图4所示。

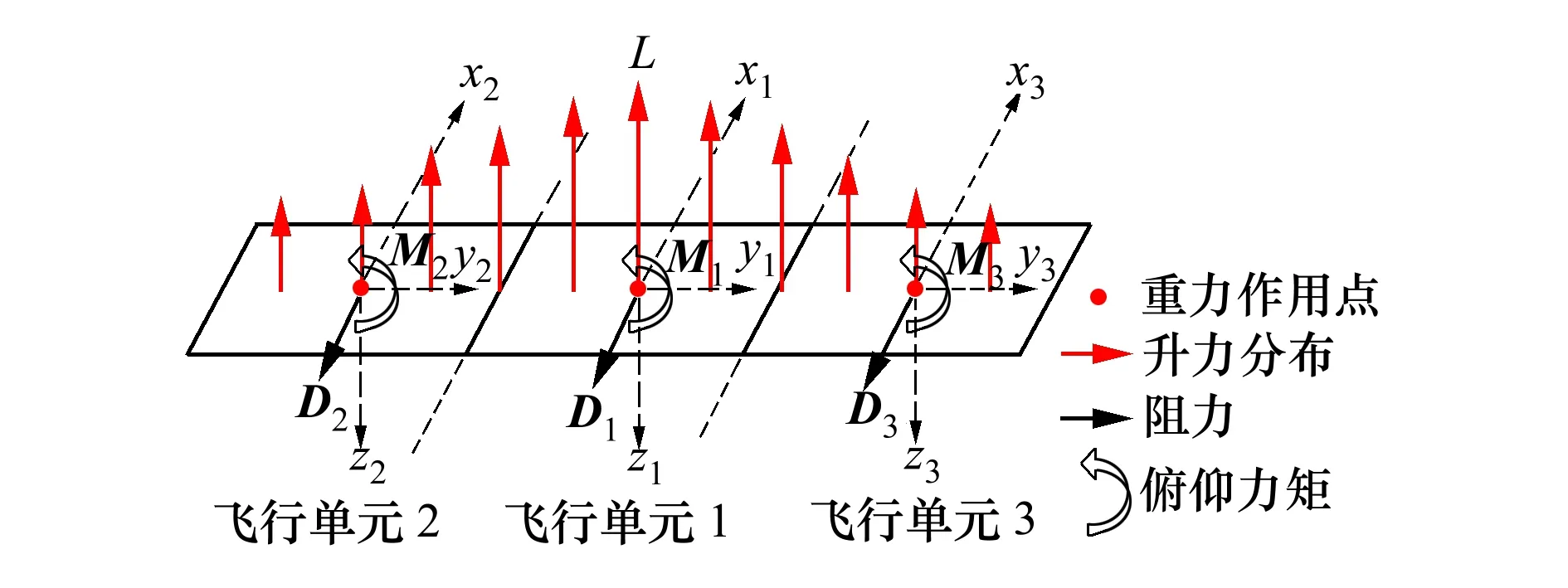
图4 气动力模型示意图

这种气动力分布形式导致飞行单元2与飞行单元3会产生附加的滚转力矩,通过对数据库拟合可以得到飞行单元各自的气动力模型。任意飞行单元所受到的气动力在气流坐标系下的表达式可以统一写成如下形式

(17)

式中,j表示与飞行单元i相邻的飞行单元。φij表示飞行单元i与飞行单元j之间的相对滚转角。CDφij和CLφij为气动力耦合项,在本文中,这些耦合项表达的含义是各翼段相对单体气动力的增量对φij的导数。V是质心相对来流的合速度,S为机翼面积,CCβ、CCp和CCr分别为侧力系数对侧滑角的导数、侧力系数对滚转角速度的导数和侧力系数对偏航角速度的导数,CLq为升力系数对俯仰角速度的导数。

飞行单元所受到的气动力矩的表达式为

(18)

式中,Clφij,Cmφij和Cnφij为气动力耦合项,其含义为各翼段相对单体气动力矩的增量对φij的导数。l为机翼的展长,cA为机翼的平均气动弦长,Clβ为滚转力矩系数对侧滑角的导数,Cnβ为偏航力矩对侧滑角的导数,Clp和Clr分别为滚转力矩系数对滚转角速度的导数和滚转力矩对偏航角速度的导数。Cnp和Cnr分别为偏航力矩系数对滚转角速度的导数和滚转力矩对偏航角速度的导数。

由于多体动力学模型是在惯性坐标系中推导得到的,因此将气动力添加到动力学模型中时,需要先通过坐标系转化矩阵Lba将气流坐标系下的气动力转换到机体坐标系下,再通过转换矩阵A(0,i)将气动力转换到惯性坐标系下

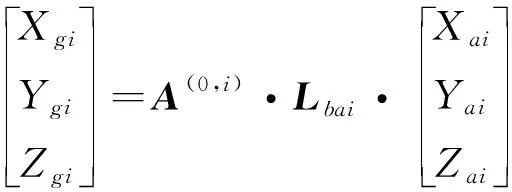
(19)

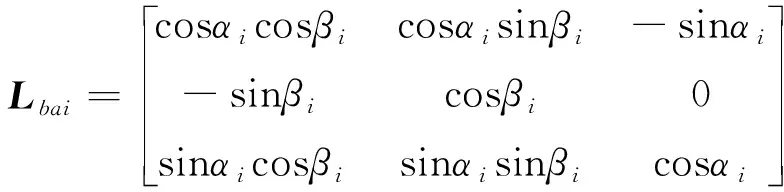
3 折叠型多体飞行器动力学特性研究

3.1 自由铰链连接下三体飞行器的动力学特性

将3个翼段之间通过自由铰链连接组成三体飞行器,飞行器与飞行器之间无卷曲弹簧连接。将每个翼段定义为独立的飞行单元,则三体飞行器各飞行单元模型的主要几何参数如表1中所示。

表1 模型的主要几何参数

设置三体飞行器的初始状态,给定飞行单元2和飞行单元3初始滚转角扰动,其中位置和姿态角的初始条件为

绝对速度和姿态角速度的初始条件为

从图5滚转角的动态响应曲线中可以看出,自由铰链连接的三体飞行器在初始滚转角扰动作用下飞行单元2与飞行单元3的滚转角会单调发散。由此可见,自由铰链连接的三体飞行器具有先天不稳定问题。安朝等在多体组合式无人机飞行力学稳定性分析及增稳控制研究[13-14]中得到了相同的运动特性,不同于传统飞行器,自由铰链连接的多体飞行器系统具有不稳定的复合运动振动飞行模态,该复合模态主要是由于飞行单元之间的相对滚转导致。

图5 滚转角随时间的变化曲线

3.2 柔性连接下三体飞行器的动力学特性

在自由铰链连接的三体飞行器的基础上,将飞行单元之间通过卷曲弹簧进行柔性连接,研究柔性连接对三体飞行器动力学特性的影响。

在多刚体动力学模型的基础上,添加线弹性柔性连接模块。同时设置飞行单元之间的卷曲弹簧刚度系数为5(N·m)/rad,其余初始状态与3.1节中相同,数值仿真的计算结果如图6所示。

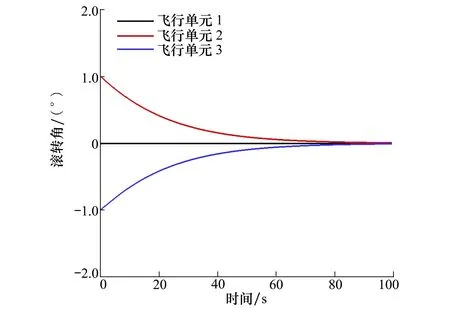
图6 滚转角随时间的变化曲线

对比图5与图6的动态响应曲线,从滚转角的动态响应曲线中可以看出,在相同的初始滚转角扰动情况下,自由铰链连接的三体飞行器滚转角单调发散,而柔性连接下的三体飞行器滚转角收敛,说明卷曲弹簧的恢复力矩对于三体飞行器的复合运动振动飞行模态而言具有一定的增稳作用。

3.3 连接刚度系数对三体飞行器动力学特性的影响

接下来将研究在相同强度的短时突风扰动作用下,柔性连接刚度系数的大小对三体飞行器动力学特性的影响。短时突风扰动的强度为2 m/s。设置三体飞行器的连接刚度系数分别为10,100,1 000,10 000 (N·m)/rad。

从图7中滚转角的动态响应曲线中可以看出,相同强度的短时突风扰动下,连接刚度系数越大,受到相同强度扰动后,飞行单元2与飞行单元3的滚转角变化幅值越小,即左右飞行器的摆动幅度越小。从数值仿真结果中可以看出,当刚度系数增加10%,三体飞行器受扰动后摆动的幅值相应减少15%。说明连接刚度系数越大,对多体飞行器复合运动模态的增稳效果越好。除此之外,随着连接刚度系数增大,飞行单元2与飞行单元3的滚转角变化由单调收敛变为振荡收敛,且连接刚度系数越大,周期振荡的频率越高。

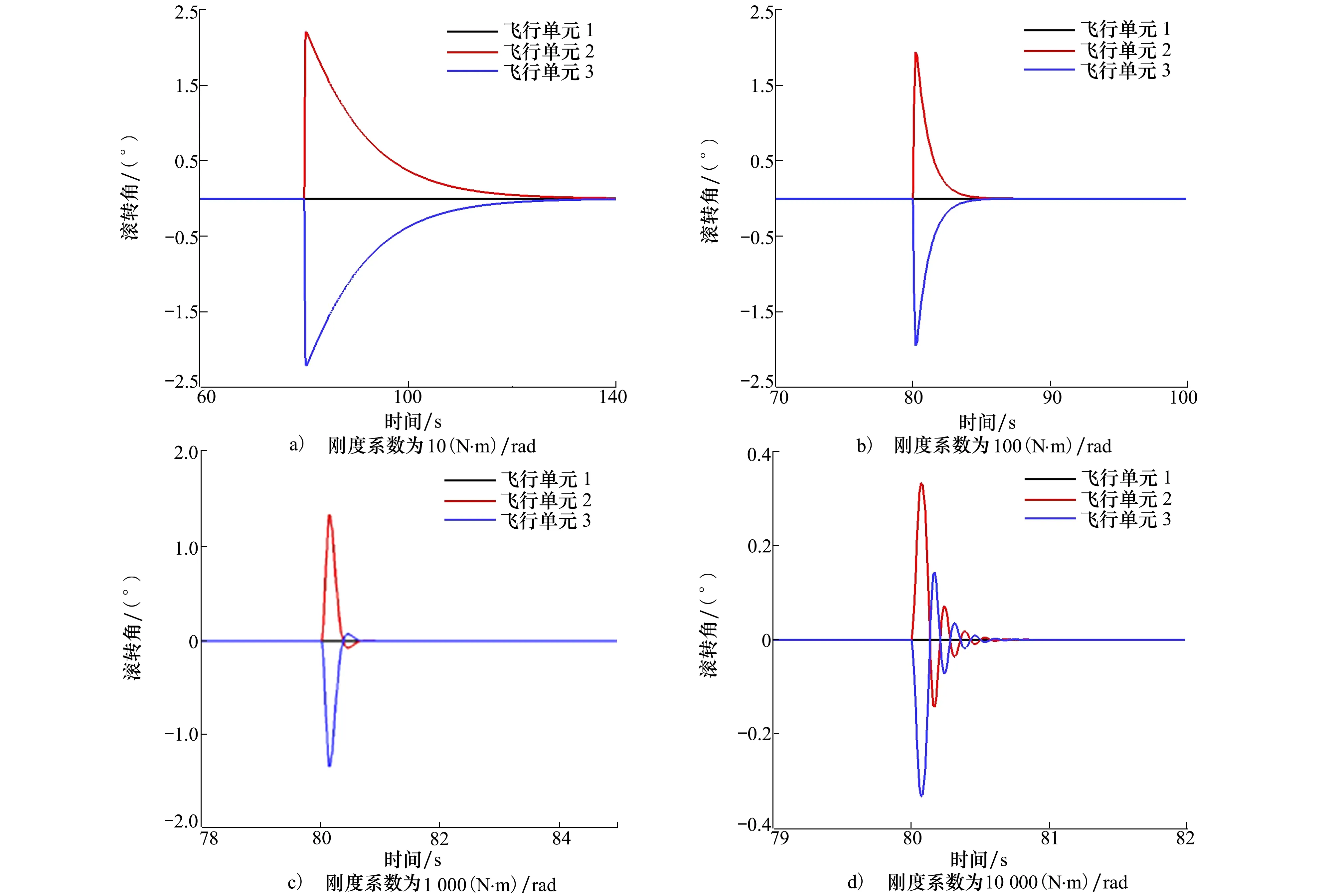
图7 滚转角随时间的变化曲线

3.4 连接刚度系数与最大初始折叠角之间的关系

本节主要研究初始折叠角与连接刚度系数大小之间的关系对折叠型三体飞行器动力学特性的影响。

由于折叠角并未直接出现在动力学方程中,需要先推导出各飞行单元重心的广义坐标与折叠角之间的关系,再将广义坐标作为初始量输入到动力学方程中。折叠型三体飞行器折叠时的三刚体简化示意图如图8所示。

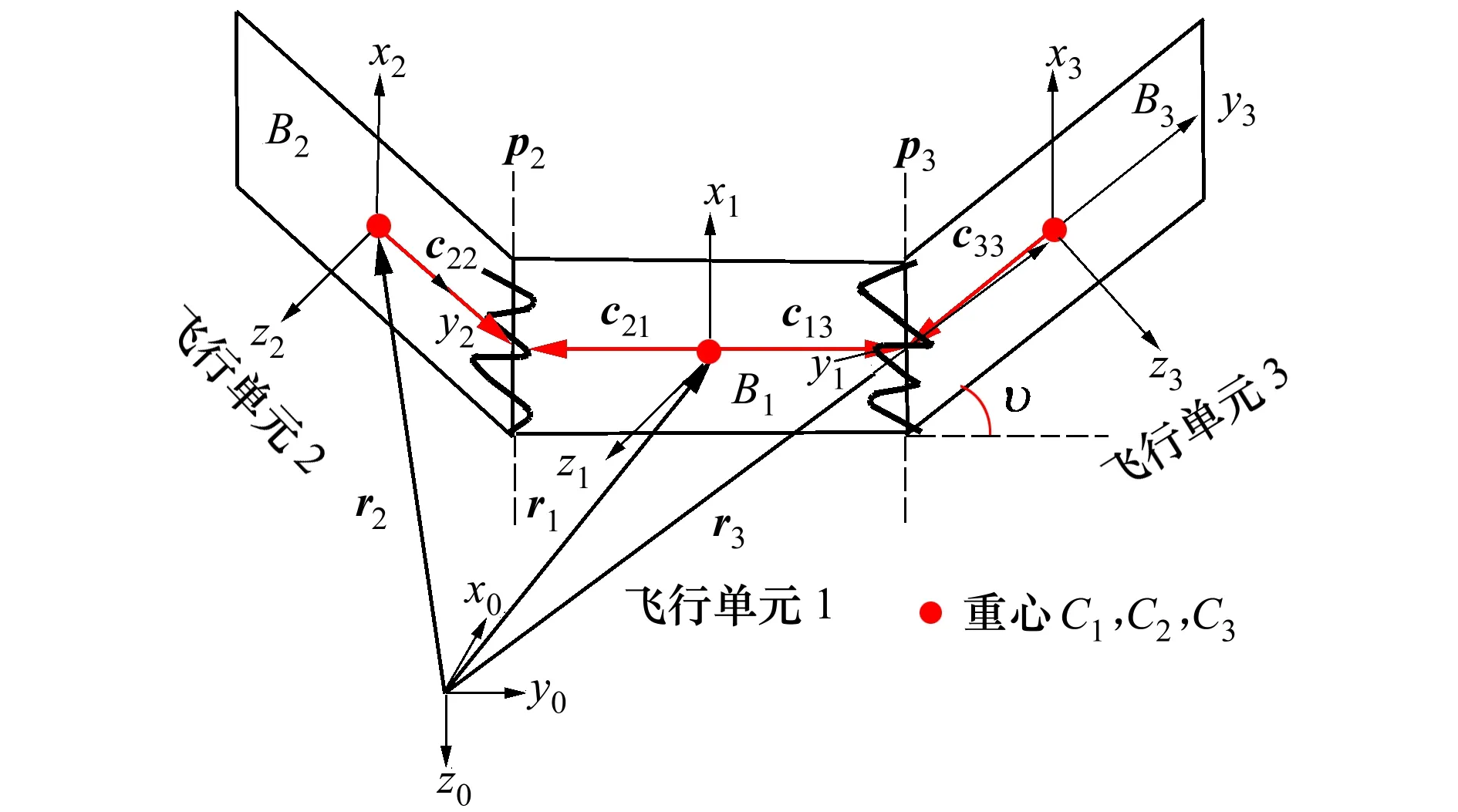
图8 折叠时的三刚体简化示意图

设折叠角为ϑ,规定三体飞行器向上折叠时,折叠角为正,反之为负。假设三体飞行器是对称折叠,则左右两边的折叠角相等。首先推导飞行单元2的绝对坐标与飞行单元1的绝对坐标和折叠角之间的关系。从图8中可得到r1和r2之间的矢量关系式

r2=r1+c21-c22

(20)

将其投影到惯性坐标系下,从而得到如下的表达式

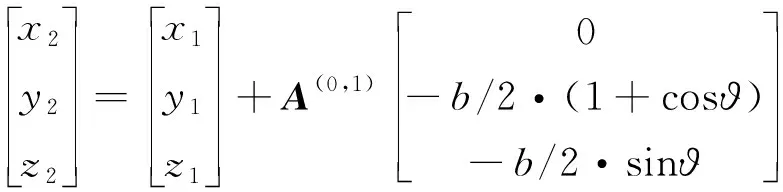
(21)

同理,通过推导能够得到飞行单元3的绝对坐标与飞行单元1的绝对坐标和折叠角之间的关系。

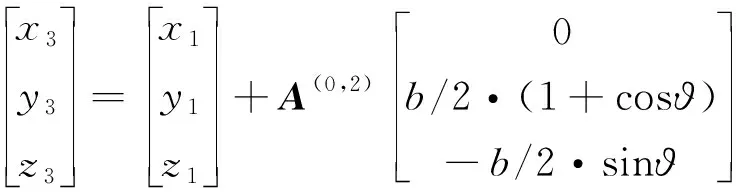
(22)

设置连接刚度系数分别为20和50(N·m)/rad,初始折叠角ϑ分别为10°,20°和-20°。飞行单元1的位置和姿态的初始状态为

飞行单元2和飞行单元3的绝对坐标由(21)式和(22)式来确定,速度与姿态角速度的初始条件与3.1节中相同。对折叠型三体飞行器展开过程进行仿真,得到的动态响应曲线如图9～11所示。

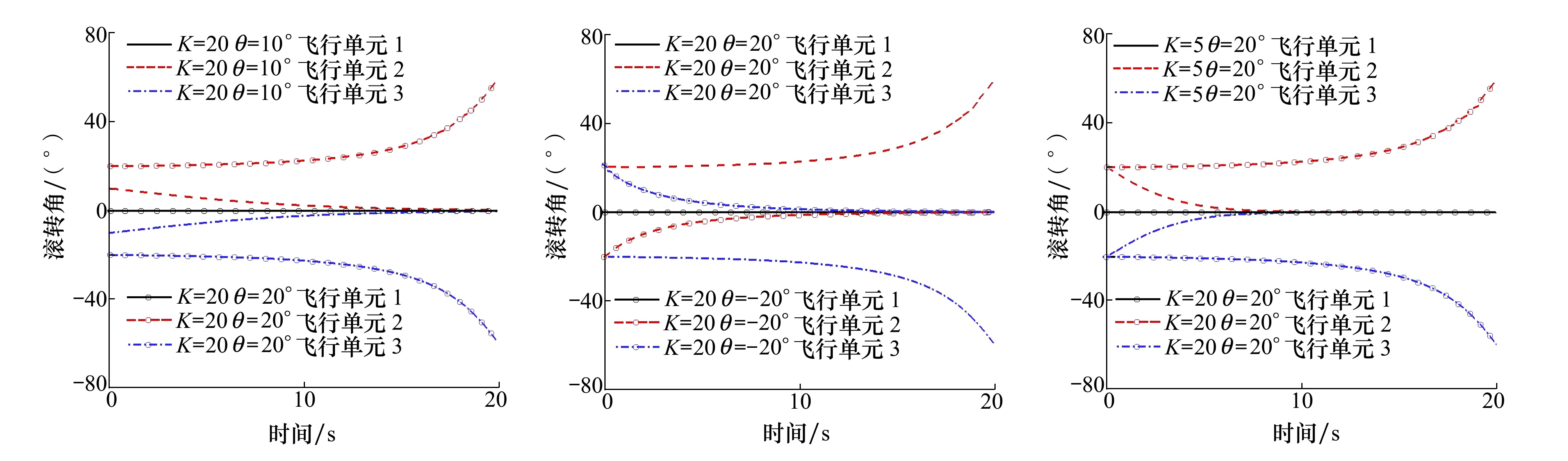
图9 滚转角随时间的变化曲线 图10 滚转角随时间的变化曲线图11 滚转角随时间的变化曲线

从图9～11滚转角的动态响应曲线中可以得到以下结论:①飞行单元之间的连接刚度系数一定情况下,当初始折叠角较小的时候,飞行单元2和飞行单元3通过上下扑动最终整体趋向稳定。当初始折叠角较大时,飞行单元2与飞行单元3则无法恢复到平衡位置。②在连接刚度系数相同的情况下,三体飞行器向上折叠和向下折叠相同的角度,向上折叠的三体飞行器无法正常展开,而向下折叠的三体飞行器能够正常展开并恢复到稳定状态,说明三体飞行器向上折叠和向下折叠对应的最大初始折叠角不同。③三体飞行器之间的连接刚度系数越大,向上折叠的最大初始折叠角越大。

导致这些现象的原因主要在于气动力对铰接点的力矩、重力对铰接点的力矩和连接刚度带来的恢复力矩三者之间的相互影响,如图12所示。

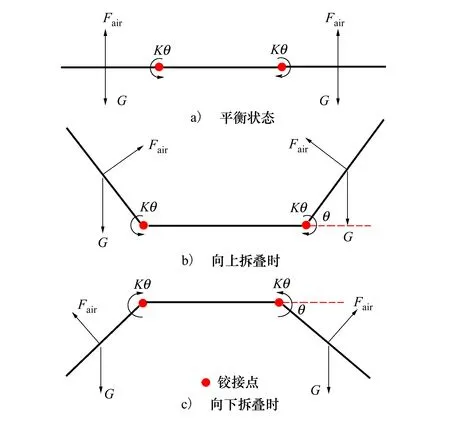
图12 三体飞行器折叠时的受力示意图

从图12c)可以看出,当三体飞行器向下折叠时,气动力产生的附加力矩方向与连接处的恢复力矩方向相同,都能够使左右飞行器恢复到平衡位置,而且这2个力矩之和大于重力对铰接点的力矩,因此向下折叠时,折叠型三体飞行器更容易恢复到平衡状态且稳定性更强。而当三体飞行器向上折叠的时候,如图12b)所示,气动力产生的附加力矩方向与连接处的恢复力矩和重力矩方向相反。气动力Fair对铰接点的力矩会使折叠状态的三体飞行器远离平衡状态,连接处的恢复力矩与重力矩则是让三体飞行器恢复到平衡状态。当气动力起主导作用时,三体飞行器会远离平衡位置而发散,当连接处的恢复力矩和重力矩起主导作用时,三体飞行器会恢复到平衡状态并稳定飞行。由此可见,相同连接刚度系数下,向下折叠的三体飞行器更有利于展开。接下来将推导气动力对铰接点的力矩、重力对铰接点的力矩和连接刚度带来的恢复力矩三者之间的关系。

通过受力分析可以得到平衡状态时气动力、重力与扭簧恢复力之间的关系

Fair·bs=G·bs·cosθ+K·θ

(23)

式中,bs为半展长。当三体飞行器向上折叠时,由于初始速度为10 m/s保持不变且初始迎角为0°保持不变,因此初始气动力基本保持不变,气动力对铰接点的力矩也基本保持不变,即(23)式左边为定值。但是重力G对铰接点的力臂减小,重力对铰接点的力矩减小,扭簧的恢复力矩反而增大。如图13所示,MG为重力矩,Mk为卷曲弹簧的恢复力矩,ΔM为重力矩与恢复力矩整体的增减量。在刚度系数一定的情况下,初始折叠角较小的时候,恢复力矩的增加量大于重力矩的减小量,此时三体飞行器能够恢复到平衡状态,当初始折叠角较大的时候,恢复力矩的增加量小于重力矩的减小量,此时,三体飞行器无法恢复到平衡状态。由此也可以看出,连接刚度系数越大,恢复力矩随折叠角增加的增加量也越大,能够稳定展开的初始折叠角也就越大。

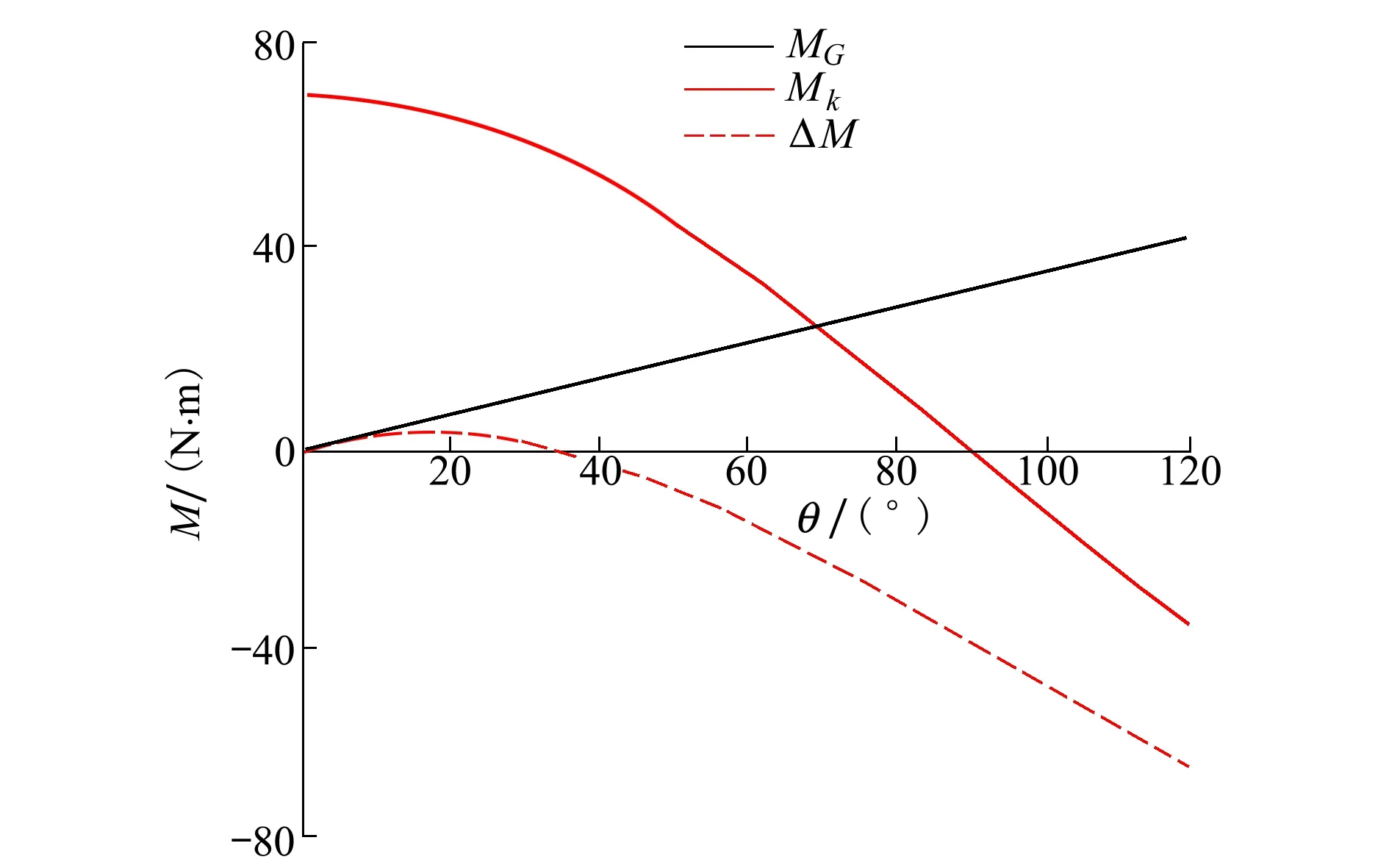
图13 重力矩与恢复力矩随折叠角变化的关系曲线

因此,通过理论推导和数值仿真计算能够得到折叠型三体飞行器在展开过程中关于连接刚度系数与最大初始折叠角的稳定域包线,如图14所示,包线范围内,水平发射的折叠型三体飞行器能够稳定展开并过渡到平稳飞行。而包线范围外,折叠型三体飞行器会失稳。

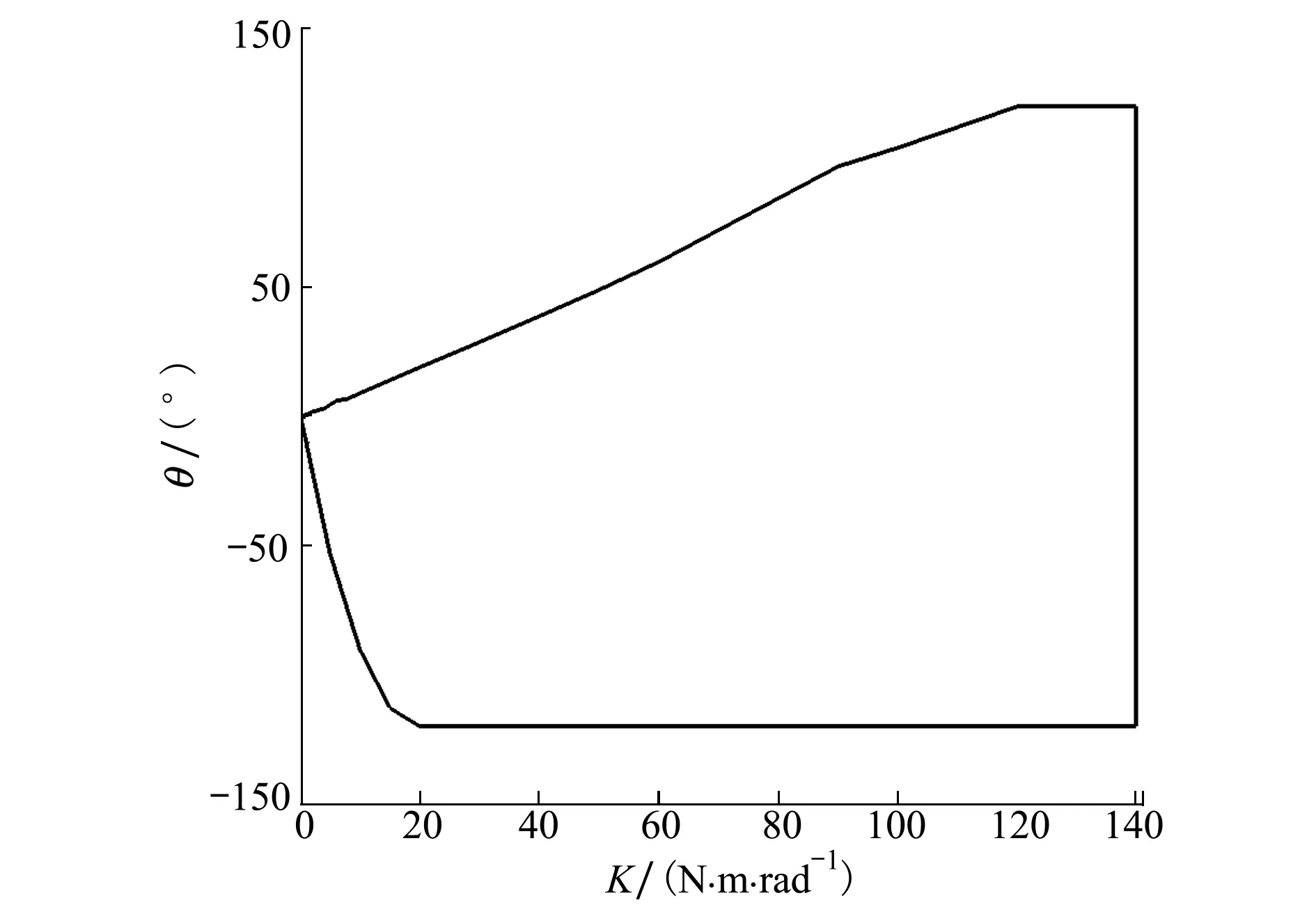
图14 稳定域包线

4 结 论

本文采用绝对坐标方法和拉格朗日乘子法建立了折叠型多体飞行器的多刚体动力学模型,并在多刚体动力学模型的基础上添加了线弹性柔性连接模型。通过对自由展开过程中飞行状态的描述分析了多体飞行器在自由展开过程的动力学特性。该方法建立的非线性动力学模型能够清晰地描述柔性连接下的多体飞行器在自由展开过程中各飞行单元的运动状态。而且此仿真模型基于模块化思想,便于修改参数,可以在多种状态下进行数值仿真计算。

除此之外,通过数值仿真计算,针对折叠型多体飞行器而言,总结得到了以下几点结论:

1) 自由铰链连接的三体飞行器的复合运动具有不稳定的复合运动振动飞行模态,若进行柔性连接,即在铰链处施加卷曲弹簧,对于三体飞行器而言,具有增稳的作用。相同强度的短时突风扰动下,当刚度系数增加10%,三体飞行器受扰动后摆动的幅值相应减少约15%。随着连接刚度系数的增大,飞行单元2与飞行单元3的滚转角变化由单调收敛变为振荡收敛,且连接刚度系数越大,周期振荡的频率越高。

2) 在相同连接刚度系数以及折叠型三体飞行器能够稳定展开条件下,三体飞行器向上折叠和向下折叠对应的最大初始折叠角有所不同,向下折叠所对应的最大初始折叠角更大,说明了向下折叠的三体飞行器的稳定性更强。

3) 通过理论推导和大量的数值仿真计算,能够得到折叠型三体飞行器的连接刚度与最大初始折叠角的稳定域包线,包线范围以内的折叠型三体飞行器能够稳定自由展开,而包线范围以外的折叠型三体飞行器在展开过程中会失稳。