明晰算理 掌握算法*
——从一道模考题谈运算素养的培养
2023-07-19江苏省常州市第二中学213000
江苏省常州市第二中学 (213000) 许 兵
罗增儒教授指出:一个数学问题,只有在得出多个解法之后,才会对问题的实质有真正的了解,才能体会不同的思维所引起的不同运算方式,学生的运算能力会在不同的思维中得以比较和提升.好的问题会蕴含多种审视视角,能帮助学生巩固基础知识,训练基本技能,明了在问题处理过程中会遇到的困惑、障碍及易错处.笔者以江苏省无锡市高三期末解析几何题为例,引导学生从设线和设点两个角度正确理解运算对象,选择合适的运算方法,优化运算程序,提高模型识别能力,提高运算能力,从而提升学生的数学运算素养.
一、试题呈现


图1
本题属于直线与椭圆的综合问题,主要考查椭圆的标准方程、直线的方程、直线与椭圆的位置关系等基础知识,考查学生推理论证能力和运算求解能力,以椭圆的定值问题为载体考查学生分析问题和解决问题的能力.立意深刻,有内涵,是一道很经典的解析几何题.
二、解法探究
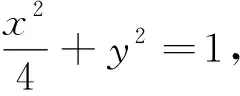
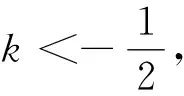
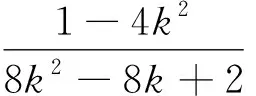
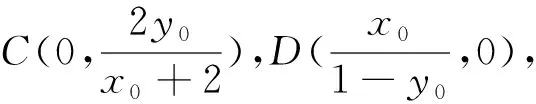

三、性质推广
“好的问题如同某种蘑菇一样,它们都是成堆地生长的,找到一个以后,你应该在周围找一找,很可能附近就有好几个”.波利亚的比喻形象而生动地说明了数学问题之间存在着紧密联系.无锡模考题可谓是2016年北京高考文科卷中解析几何题的变式,根据题干信息可以证得四边形ABDC的面积是定值,因此求ΔPCD面积的最大值即求ΔAPB面积的最大值,由于AB的长度已知,所以求ΔAPB面积的最大值便迎刃而解.笔者经过探究发现,当点P在其他象限时,此类四边形ABDC的面积有如下性质.

(1)当点P在第四象限时,凸四边形ACDB的面积为ab;
(2)当点P在第一、三象限时,凹四边形ACDB的面积为ab;
(3)当点P在第二象限时,A,B,C,D四点与点P构成蝴蝶型,且SΔPCD-SΔPAB=ab.
四、反思感悟
《普通高中数学课程标准(2017年版)》中提出,数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.数学运算主要表现为:理解运算对象,掌握运算法则,探究运算思路,求得运算结果.但在日常的数学解题过程中,学生往往关注的是运算法则、运算结果的正确性,但对运算对象的理解、运算思路的探究、算法的设计与优化往往容易忽视,因此“设线还是设点、变元怎么消、表达式怎么化简”成为解析几何求解的“三重门”.线参法和点参法是解决动直线与圆锥曲线相交问题的基本方法.在解题过程中要有目标意识,将问题中的信息、目标元有机联系起来,确定题设变元、构建变元之间的关系,是设点还是设线的运算核心,也正是学生算法思想的体现.
在用设点法或设线法求解时,若能用某个点的坐标或某直线方程中的某一个或几个变量去表示其余的点的坐标或直线的方程,问题就迎刃而解了.选取什么量将题目中的信息联系起来,如何才能将已知信息转化到所设变量上去.教师要引导学生直面困难,在求解过程中要学会将算理和算法结合起来,逢山开路,遇水搭桥.既要会从代数角度运算,也要学生会观察图形特征;既要能直接“硬算”,也要会选择“方法”简算;既要能选好求解切入点,又要会中途调整方向、追根溯源、优化解法﹑把握本质.解题中因思考而行动,因行动而理解,因理解而优化,促进解析几何中代数与几何的综合能力的升级与发展,从而提升学生的数学运算这一核心素养.
