多层地下深埋车站站台火灾工况下站台门漏风量计算分析

高 伟 王方敏 王圣杰 任治立 肖益民

（1.中国电建集团华东勘测设计研究有限公司 杭州 310014；2.重庆大学土木工程学院 重庆 400045）

0 引言

自21 世纪以来，地铁凭借其运行速度快、运送能力大、环境污染小、综合经济效益高等优势迅速发展起来，并已成功成为国内中大型城市的主要交通工具[1]。然而，地铁快速发展的同时，地铁车辆及车站的火灾安全问题成为备受关注的重点[2]。根据相关的统计结果[3]，大量火灾实例中，有80%以上的人员伤亡都是由于没能及时疏散导致吸入火灾所产生的高温烟气及有毒气体中毒窒息而死，所以楼扶梯等疏散通道的烟气控制具有重要意义。《地铁设计规范》（GB 50157-2013）[4]和《城市轨道交通技术规范》（GB 50490-2009）[5]规定：当车站站台发生火灾时，应保证站厅至站台的楼梯和扶梯口处具有能够有效阻止烟气向上蔓延的气流，且向下气流的速度不应小于1.5m/s。地下多层深埋地铁车站的站台层发生火灾时，由于地铁出入口至站台层补风的阻力较大[6]，通常选择关闭站台门，以防止大量空气由隧道向站台流入而导致楼扶梯口向下的风速降低，对人员疏散安全造成威胁。但地铁站台门处于关闭状态时仍会存在缝隙[7,8]，李俊等人在某地铁车站的测试中发现，列车运行站台门关闭时站台和隧道之间仍有较大风量的变化[9]。

目前国内外对于站台门漏风量的研究主要采取数值模拟、通风网络计算和现场实测等方法。杨巨澜等人[10]采用STAR-CD 对上海某地铁站进行数值模拟，模拟结果显示站台门漏风量随地铁排热风机压头增大而增大。项毅[11]以某典型地铁站台为研究对象，结合CFD 和SES 软件，计算出列车停站时间段内站台门系统的渗透风量。李俊[9]和赵成军[12,13]等人分别通过通风网络计算法对列车停站阶段站台门的漏风量进行了计算。陈玉远等人[14]通过对武汉某地铁车站漏风量的实测，得到了漏风量的变化规律和影响因素。

但上述研究主要针对地铁正常运行工况下通过站台门处的渗漏风量计算，未见在火灾工况下站台门处于关闭状态时的渗漏风量的讨论。本文以成都某地下深埋车站为研究对象，通过通风网络法计算出地铁车站内各通风支路阻抗，将其计算结果与CFD 模拟结果进行比较，验证了计算结果的准确性。在此基础上，本文还建立了漏风量计算的通风网络模型，应用该模型对研究对象在火灾工况下站台门的漏风量进行了计算。

1 工程概况

某地铁车站为地下六层岛式车站，其结构特征是：地下二层为站厅层，地下六层为站台层，站厅层公共区面积为4199m2，层高7.9m，站台层公共区面积为2641m2，有效层高5.65m，车站站台埋深40m，属于深埋型车站。站台两侧为行车区，即车站隧道，通过站台门系统将站台和隧道隔离。站厅层与站台层通过四台自动扶梯、一台步行楼梯相连，布置如图1、图2 所示。

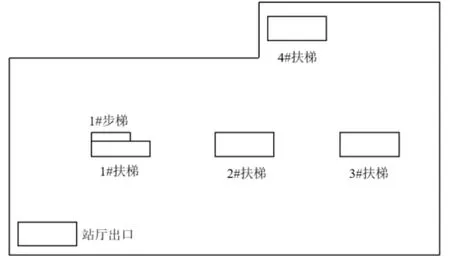
图1 站厅层楼梯扶梯布置示意图Fig.1 Schematic layout of staircase escalator at station hall level

图2 站台层楼梯扶梯布置示意图Fig.2 Schematic layout of staircase escalator at station

根据通风空调系统设计方案，当站台火灾发生时，采用大系统站台层排烟系统结合车站隧道排热风机协同排烟模式。即开启两台站台层空调大系统额定风量为108000m3/h 的排烟风机和两台轨顶排热风道内额定风量为144000m3/h 的辅助排烟风机，同时关闭站台层的空调系统与站台门，通过通道楼梯口自然补风。整体系统图如图3 所示。

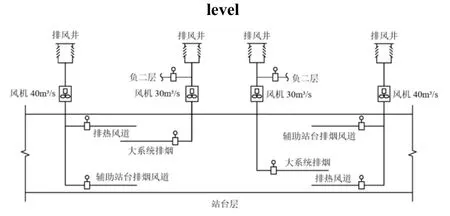
图3 站台层通风排烟系统图Fig.3 Platform level ventilation and smoke exhaust system diagram

2 研究方法

2.1 通风网络模型

2.1.1 地铁车站火灾工况通风网络模型

站台层发生火灾时，站台门关闭的同时排烟风机开启，站台内形成负压，室外空气通过车站出入口和站台门缝隙进入站台。此时出入口通道、楼梯、站台门及活塞风道构成了一个通风网络系统，图4为该车站的通风网络模型。

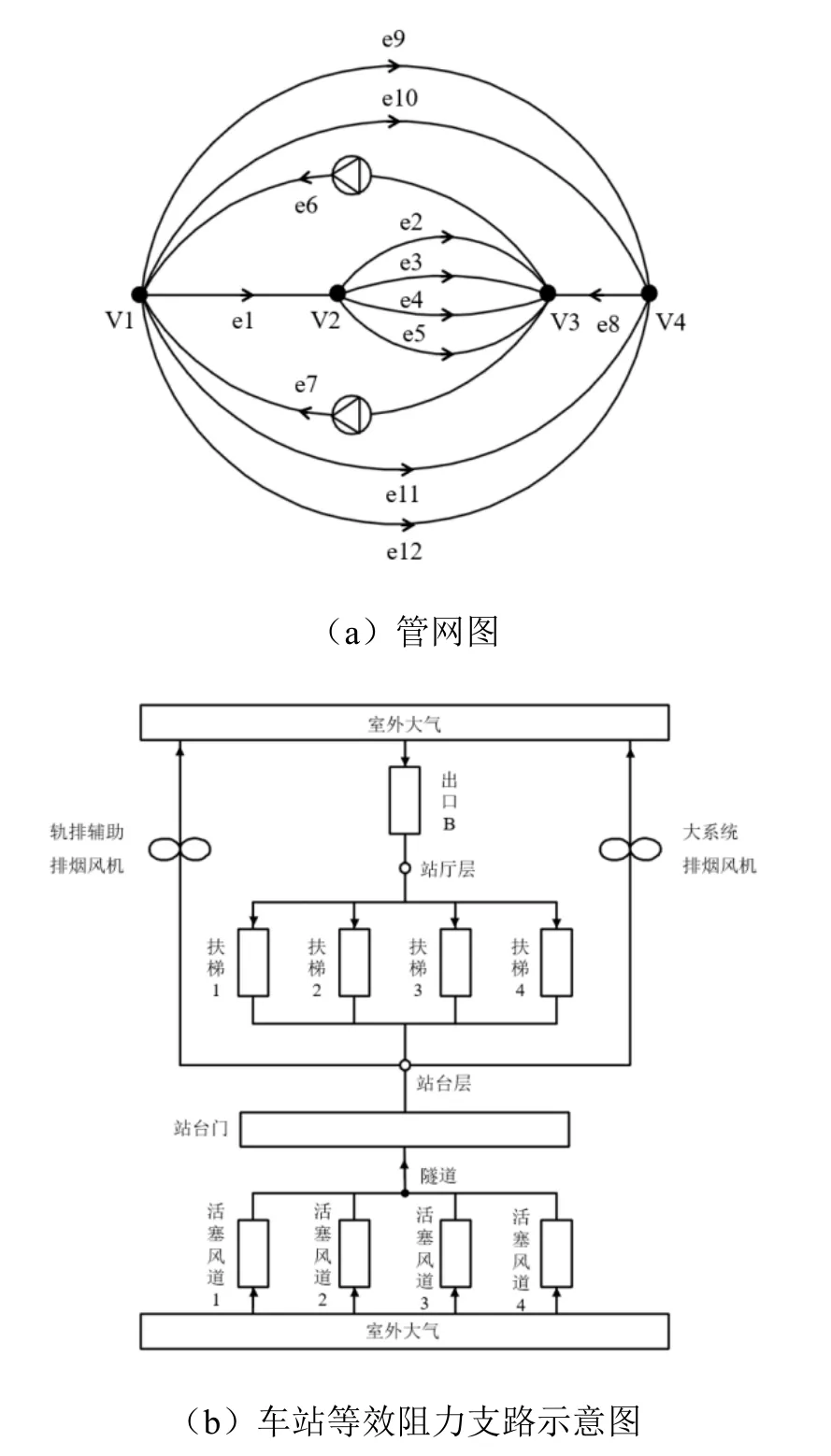
图4 车站通风网络模型Fig.4 Station ventilation network model

2.1.2 通风网络理论

（1）通风网络即用图论的方法对复杂的通风系统进行简化，将通风系统变成一个由线、点及其属性组成的系统。通风网络理论遵守风量平衡定律和风压平衡定律[15]：

式中：Qi为流入与流出某节点或回路各分支的风量，m3/s；hi为任一回路中各分支的风压，Pa。

（2）串联管路中各支路流量相等，阻力损失等于各支路阻力损失之和；并联管路各支路阻力损失相等，总流量为各支路流量之和[16]。

2.1.3 通风支路的阻抗

当空气密度为常数时，管路的阻力损失h与体积流量Q的平方成正比，即：

式中：S为管路中沿程阻力和局部阻力的总阻抗，kg/m7；Q为流量，m³/s；d为管径，m；ξ为局部阻力系数；λ为沿程阻力系数；ρ为空气密度，kg/m³；l为管路长度，m；A为面积，m2。

一般而言，地铁通道中的局部阻力要远远大于沿程阻力[13]，因此在估算支路的阻抗时，可以将沿程阻力忽略，阻抗S仅与局部阻力系数ξ有关。则式（4）改为：

串联管路总阻抗等于各分支管路阻抗之和：

并联管路总阻抗的平方根倒数等于各分支管路阻抗平方根倒数之和：

由于地铁通道内局部损失计算较为复杂，将各支路内的出入口、楼梯等阻力部件简化为由门洞、弯头等基本部件的组合，然后应用式（5）、（6）、（7）计算得到支路阻抗值。基本部件的局部阻力系数根据相关文献[12]查得。

2.2 通风支路阻抗的数值模拟

因2.1.3 中通风支路的阻抗计算方法较为粗略，可采用流体力学数值模拟的方法对其计算结果的准确性进行对比验证。对排烟工况下经出入口通道、站内空间和楼扶梯的补风支路建立数值模型，根据CFD 模拟结果，可得支路进口和出口之间的压差，应用式（3）可计算出支路的阻抗值。

2.2.1 几何模型与网格划分

由于地铁车站内空间尺寸较大，内部设施较小，在建模时可以进行适当的简化，忽略车站内的小尺寸结构，比如闸机、指示牌等设施，以降低模型的复杂性同时提高计算域的网格质量。所建物理模型如图5 所示。其中站台与站厅中间立柱截面尺寸为0.9m×1.2m；站台两侧有18 个尺寸为0.5m×1.2m、1 个尺寸为0.8m×1m 的主排烟口；14个辅助排烟风口设在土建风道内侧，尺寸为0.7m×1.7m；站台层扶梯开口四周设置距离吊顶0.5m 高度的挡烟垂壁。结果的准确性，分别选取488 万、593 万、728 万、914 万及1123 万的体网格数量进行计算，站厅出入口至站台层的压力损失计算结果如图6 所示。由图可知，当网格数量由488 万增加到1123 万时，压力损失变化逐渐趋于平缓，考虑到计算时长和计算精度，本文选择网格数量为728 万的计算模型进行模拟。

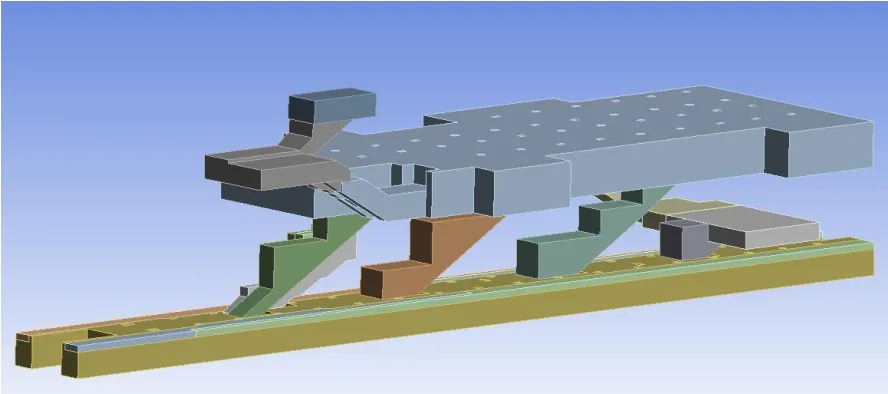
图5 地铁车站三维模型图Fig.5 Subway station 3D model

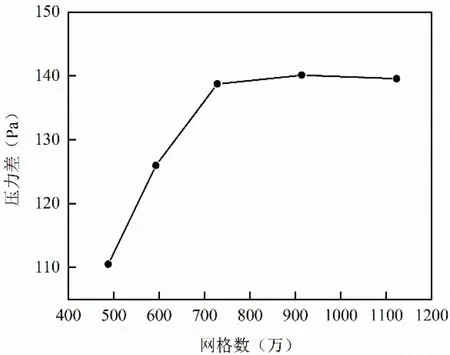
图6 出入口至站台层压力损失随网格数量变化Fig.6 Pressure loss at the entrance/exit to platform level varies with the number of grids

2.2.2 湍流模型和边界条件的确定

本研究进行CFD 模拟的目的在于计算排烟工况下地铁车站内各通道的阻抗值，采用Fluent 软件进行数值模拟，湍流模型选用Standardk-ε模型；站厅层出入口设为压力出口边界条件，开口处压力为大气压力；排烟口设为速度入口边界条件，风速根据设计排烟量计算确定；壁面设为wall 边界，不考虑车站内的热交换过程。

将车站计算域拆分成13 个子域单独划分网格，在网格划分时尽量保证截面上网格节点分布和网格密度相同，以保证交界面上的计算精度。在计算域内生成四面体网格，对楼梯口、站厅出口等流场变化剧烈的地方进行局部加密。为保证数值模拟

3 结果与分析

3.1 通风支路阻抗

3.1.1 传统方法的计算结果

由2.1.3 中的方法，用基本部件局部阻力系数得到的各支路阻抗值如表1 所示。其中站台门因性能和安装质量的差异会导致其气密性有所不同，即站台门缝隙的面积不同。本文参考李晓锋等人[17]对多个地铁车站站台门气密性的测试结果，取缝隙总面积为1.4～3.3m2进行计算。当空气流经站台门缝隙时，相当于先从一个无限大空间流入断面很小的缝隙中，再由缝隙流入一个断面很大的空间中，因此站台门缝隙处的局部阻力系数可以等效为突缩和突扩的阻力系数之和[18]。

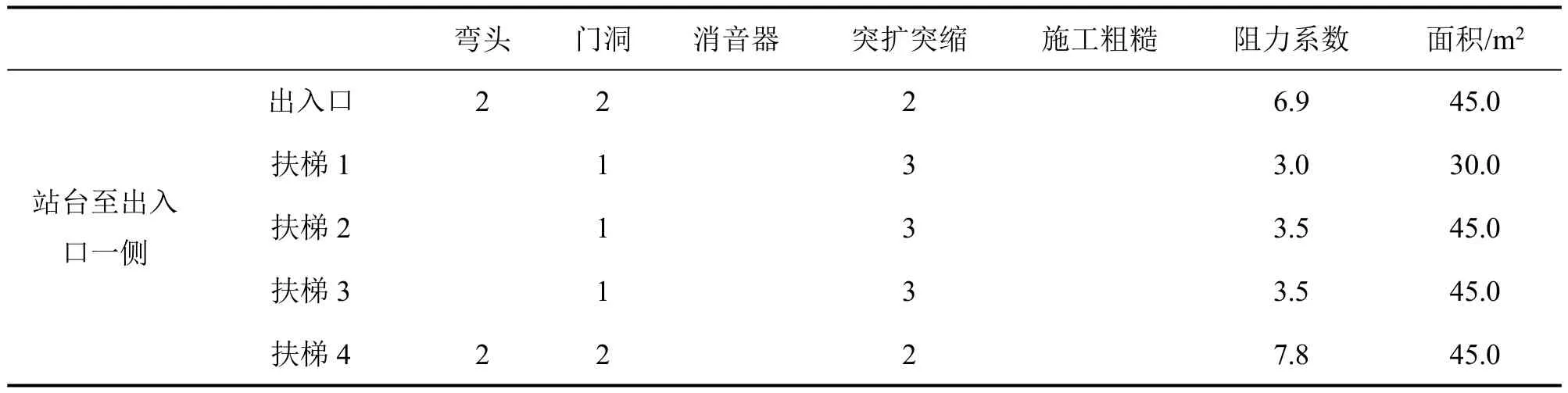
表1 站台-出口通道各支路阻抗Table 1 Impedance of each branch of platform-exit channel

根据图4 所示的各支路之间串并联关系，结合式（5）-式（7）分别计算出站台-出入口一侧的总阻抗值为4.58×10-3kg/m7，站台门-活塞风道一侧的总阻抗值范围为0.09～0.50kg/m7。

3.1.2 CFD 模拟结果与传统计算法的对比

CFD 数值模拟结果如图7-图9 所示。根据模拟结果可知站台-出入口通道的压力损失为98.15Pa，风量为140m3/s，由（3）计算可得站台-出入口通道的总阻抗为5.01×10-3kg/m7。

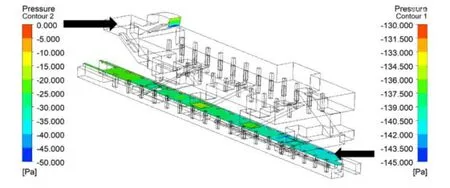
图7 站台扶梯开口高度和车站出入口全压分布图Fig.7 Platform escalator opening height and station entrance/exit full pressure distribution

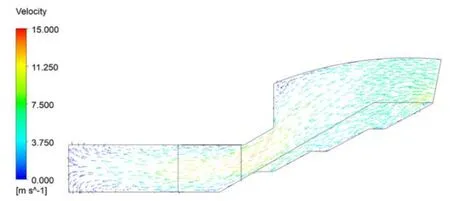
图8 地铁出入口处速度矢量分布图Fig.8 Speed vector distribution at subway entrances and exits

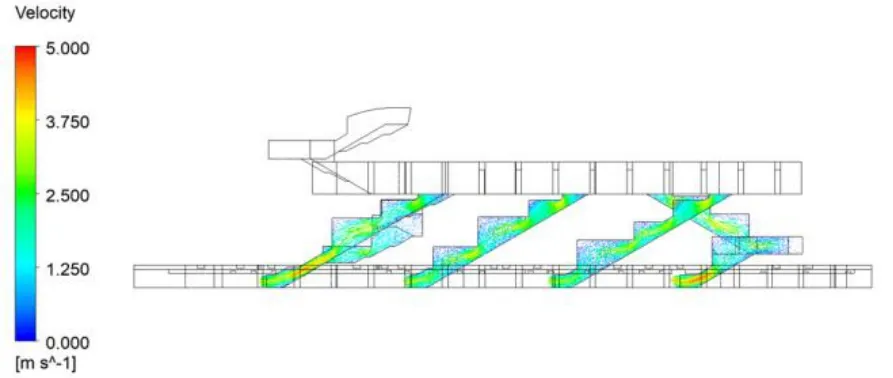
图9 四部楼扶梯截面速度分布矢量图Fig.9 Cross-sectional velocity distribution vector of four escalators

将站台-出入口一侧CFD 数值模拟的阻抗计算结果与传统计算法的阻抗计算结果进行对比，两者相差不超过10%，说明传统计算法亦能够获得较准确的地铁车站通风支路的阻抗值，同时也验证了CFD 模拟结果的可靠性。

3.2 站台门漏风量估算

由图4 可以写出站台层内气流平衡公式：

由通风网络的回路压力平衡方程，可得：

根据式（3）、（8）和（9），可得：

式中：Qexit为通过车站出入口进入站台内的风量，m3/s；QPSD为通过站台门缝隙进入站台内的风量，m3/s；Qp1为通过大系统排烟风机排出的风量，m3/s；Qp2为通过轨排辅助排烟风机排出的风量，m3/s；hexit为站台-出入口支路的总阻力损失，Pa；hPSD为站台门-活塞风道支路的总阻力损失，Pa；Sexit为站台-出入口支路的总阻抗值，kg/m7；SPSD为站台门-活塞风道支路的总阻抗值，kg/m7。

结合公式（8）、（9）、（10）可计算得到站台门的漏风量，如图10 所示。可以看出，站台门漏风量随着站台门缝隙面积的增大而增大，当缝隙面积由1.4m2增加到3.3m2时，站台门漏风量由12.2m3/s增加到25.7m3/s，占设计排烟量的比值由8.77%上升到18.34%。由公式（10）可知，站台门漏风量取决于站台-出入口支路阻抗平方根与站台门-活塞风道支路阻抗平方根的比值，当车站内部各通风支路阻抗确定时，减小漏风量的关键为减小站台门缝隙面积，即提高站台门的密闭性。

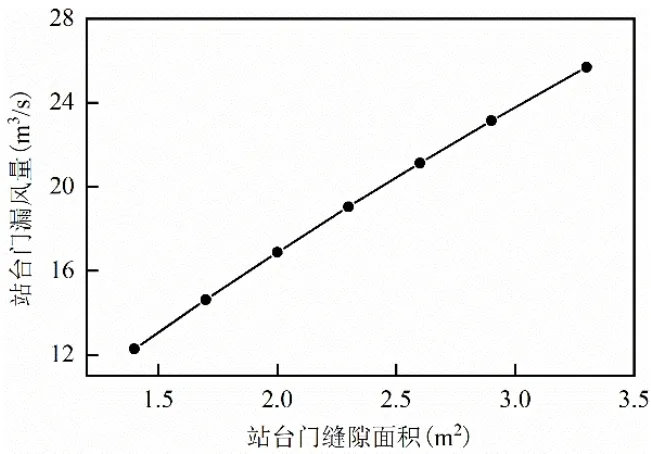
图10 站台门漏风量随缝隙面积变化Fig.10 Variation of air leakage from station doors with gap area

4 结论

关闭站台门系统是解决深埋地铁车站排烟系统在站台火灾工况下楼梯口下行风速不满足规范要求问题的一种方式，但站台门处于关闭状态时仍会有部分空气由缝隙进入站台。为计算这部分漏风量，本文基于通风网络理论，计算了车站内各通风支路的阻抗值，并与CFD 数值模拟结果进行比较，两种计算方法的结果接近，验证了阻抗计算值可用于通风网络计算。

在此基础上，通过建立的通风网络模型，计算了站台门缝隙处的渗漏风量，结果表明，随着站台门的安装密闭性降低，漏风量由12.27m3/s 增加到25.67m3/s，占设计排烟量的比值为8.77～18.34%。

CFD 模拟虽然能够详细模拟出车站内气流组织和压力分布情况，但对于实际工程而言，数值模拟耗时较长，工作量大。本文研究表明，采用流体力学传统计算法的计算结果同样能够满足工程精度要求，并且更简单方便，能够节省大量计算时间。