基于曲面共形方式的干涉仪测向技术研究
2023-07-17石林艳何洋炎
李 明,石林艳,王 斌,何洋炎
(中国电子科技集团公司第五十一研究所,上海 201802)
0 引 言
共形天线是有别于平面天线的一种天线形式,其附着的载体主要包含飞机、卫星、舰船及导弹,使其能够贴合于载体表面,减弱了天线对载体动力学的影响。IEEE关于共形天线及其阵列的定义:一种共形于载体表面的,对于形状要求大于其电磁特性的一类天线,其形状主要是由空气动力或水力等因素决定的。目前研究的相控阵主要分为直线阵和平面阵2类,尽管其技术已经相当成熟,应用也极其广泛,但是仍然存在一些缺点,比如平面阵天线的波束扫面范围窄,无法实现全方位的覆盖;在一些特殊要求(空气动力学要求苛刻或隐身方面需要天线阵与非平面载体共形)条件下无法满足指标要求。相较于平面阵而言,共形阵(即曲面阵)有以下特点:提高了载体空间的利用率;减小了体积与质量,增强了设备的结构强度;扫描范围可以达到半球以上覆盖;保持了载体平台的空气动力学性能,同时又可以达到隐蔽伪装的功能[1-4]。
为实现工程应用,需进一步开展研究。国内应用于军事电子对抗领域的共形天线设备较少,这是由于共形天线辐射特性分析复杂、建模困难所致;所以现阶段更多的是进行技术攻关、理论完善。基于干涉仪体制的共形天线测向技术的国内外研究成果相对于平面阵列而言都较少,可以结合平面阵成熟的研究基础与工程经验对其进行研究分析。
依据实际的背景需求及拟采用的测向体制,为了满足基于共形天线阵列的设计要求,本文主要通过布阵构型、曲面解模糊算法及相位补偿3个方面对其展开具体研究。
1 布阵构型及其约束
当需要覆盖一个广角区域时,若利用平面阵列,则需要几个指向不同的平面阵列的组合。典型理想共形阵列的辐射单元均匀分布在光滑曲面,其辐射器的外形都与曲面曲率相匹配。
在确定具体布阵构型时需要考虑遮挡效应,由于自身形状及其局部外形以及周边物体的遮挡作用,导致电磁波无法直接照射到物体表面,通过绕射、反射到达物体表面亦或无法抵达的现象称之为遮挡效应。对于载机平台而言,无论接收天线如何布局于其表面,一定程度上都会因为载机不规则的外形导致遮挡效应的存在。在讨论共形天线布局问题时,这样的效应将会更加明显。因为其有别于平面阵相对简单的一维布局形式,考虑到基线长度问题,需要利用降维的思想,使其转化为双一维形式,从而采取一维平面更加成熟的处理技术达到精确测向的目的。同时由于遮挡作用,同一时刻某一角度并非所有阵元都参与工作,即有些阵元对于某些入射角而言是冗余的,但处于其他角度时又是正常参与测向的;所以需考虑到天线复用的问题,提高资源利用率。
主要考虑机首与机翼两处共形天线阵的布局形式。机首表面是一类圆锥曲面,机翼、机尾表面属于抛物面。首先建立机首、机尾处大阵元间距布局示意图,如图1所示。
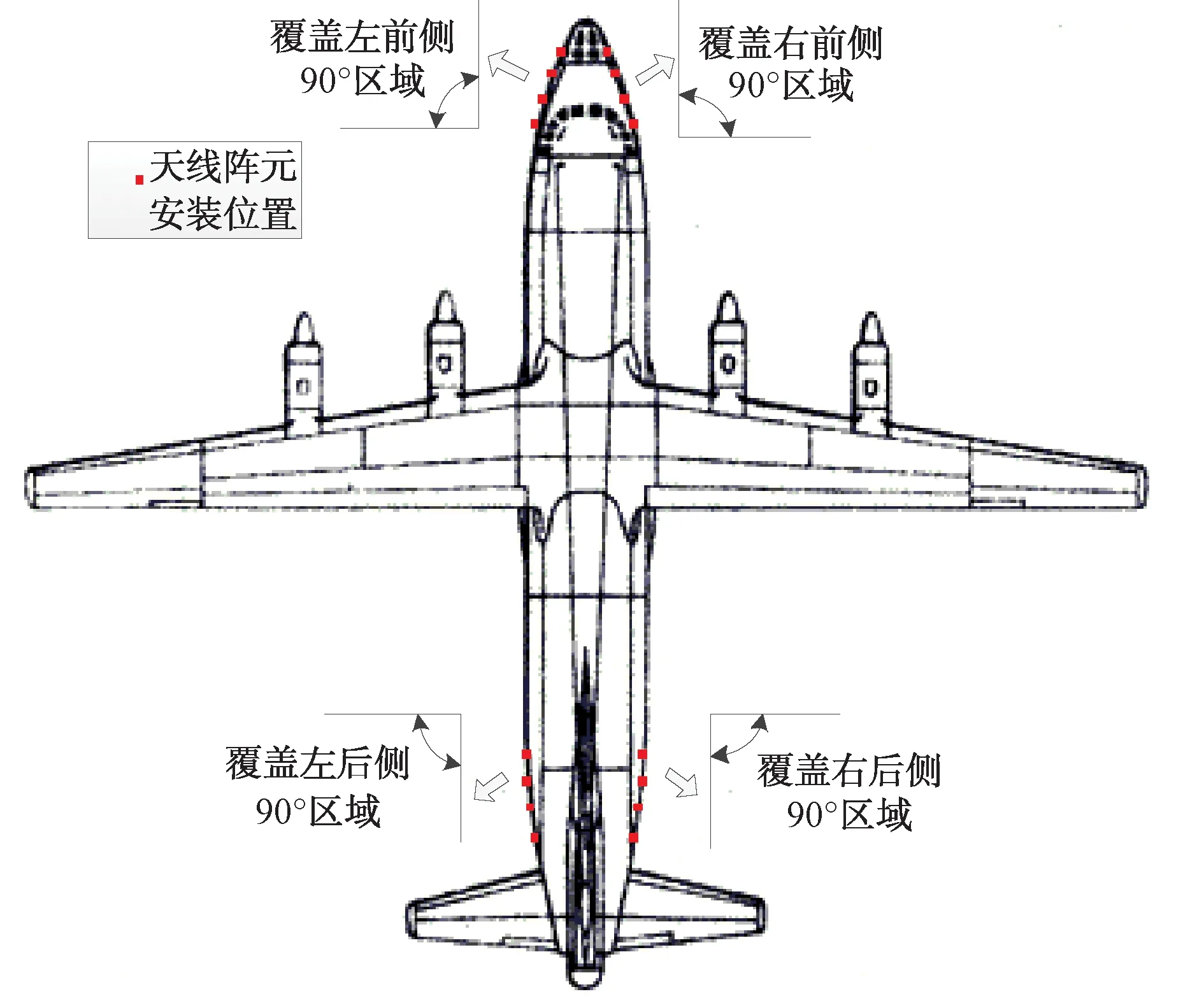
图1 机翼天线分布简化示意图(非等间距非共平面)
为了满足单阵面方位面90°覆盖的要求,现提取飞机左前侧天线阵面进行约束条件的分析。其简化示意图如图2所示。
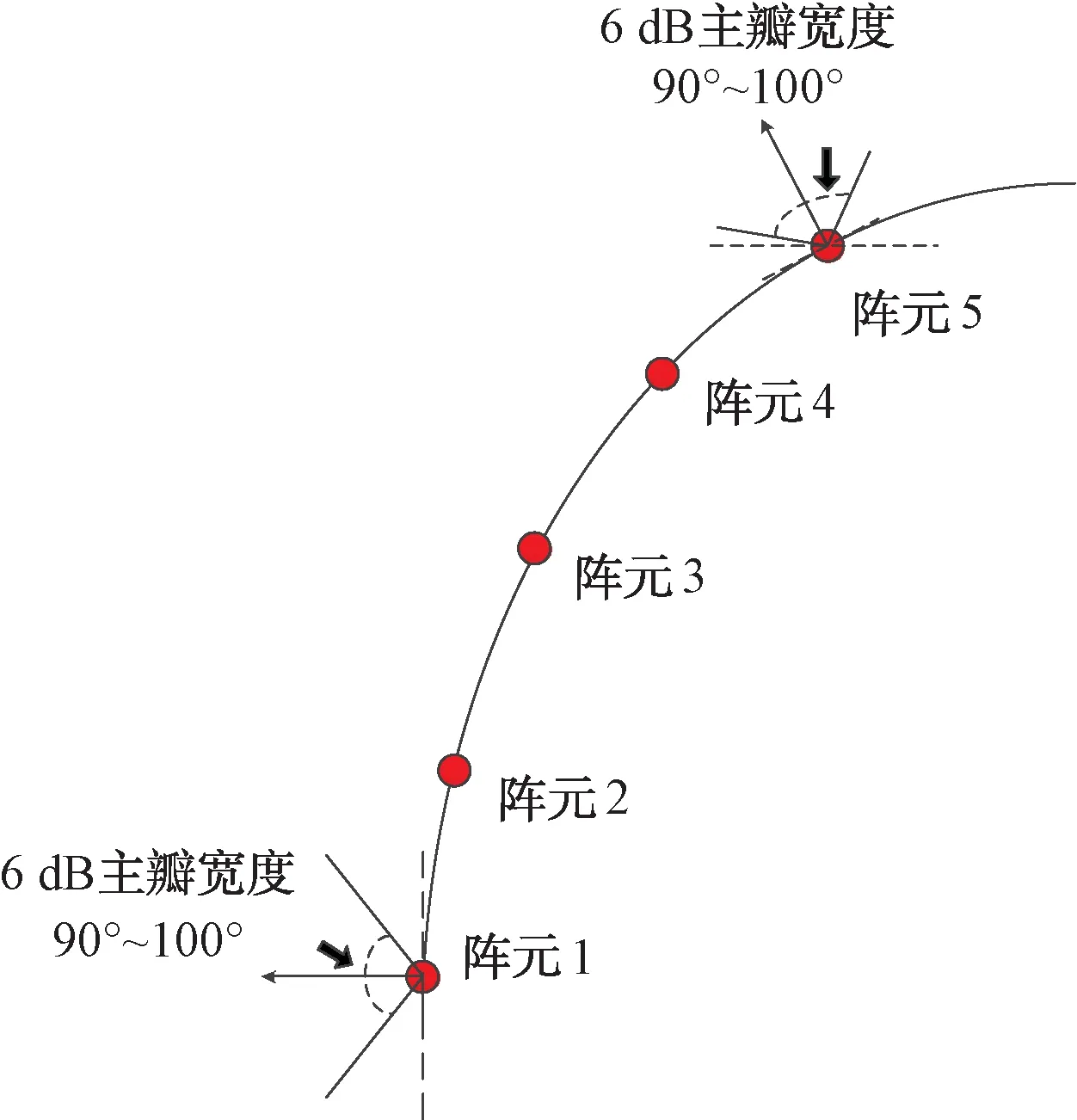
图2 单面天线单元分布示意图
为了防止副瓣接收,拟将每个90°区域覆盖范围再细分为几个小区域,每个子区域分别由对应的一组阵元完成比相法测向,从而完成相应90°区域测向,其他3个阵面测向方式类似,进而达到360°全方位的覆盖。
上述测量主要针对一维方位面的测量,拟将阵元布于机头两侧及机身后方两侧,由于与机体表面共形,各组阵元呈抛物面排布,可将其实际位置投影至一平面,可投影的依据为:对于每面入射的信号,接收端设备的高度不会对信号的波程差及遮挡效果产生影响。该思想为后续信号处理提供了便捷,且关于平面阵的处理技术是成熟可靠的。
某一阵面只负责单一方位的测向时,共形曲面在该维度水平面的投影所得到的映射点与原始位置处于同一法线方向,即该2点在来波方向上接收到的信号等路径长,如图3所示。
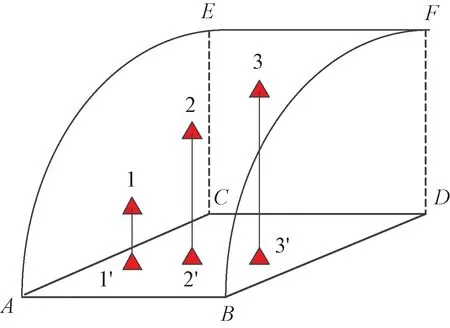
图3 投影圆面角度覆盖示意图
曲面ABFE为原始曲面,曲面ABCD为投影面,1,2,3为初始阵元位置,相对应的1′,2′,3′为在投影面上的投影点。从图3中可以看出,入射信号到达1与1′,2与2′,3与3′的路径长度一致,对于干涉仪测向而言,产生的相位差值主要是由路径差引起的。当路径差不变时,所产生的相位差值是不变的。换而言之,可以将曲面阵元位置投影至平面上,简化计算流程,利用成熟的平面干涉仪处理方式对来波信号进行数据处理,快速测得精度较高的入射角方向。
若存在遮挡效应时,因为任意时刻并非所有阵元都需要参与测向,通过信号检测,确定需要参与该区域测向的部分阵元即可。这不仅可以减少资源的开支,而且降低了计算的复杂度,进一步提升了测向的实时性。
2 曲面阵解模糊
图4给出了载体平台为曲面情形下,天线单元的安装情况示意图。h与h1分别为阵元1,2和1,3之间的高度差,d与d1分别为阵元1,2和1,3之间的水平距离。入射角度由于共形要求,天线单元会产生纵向距离,定义的入射角度与基线和入射方向之间的夹角会存在一差值,从而产生入射方向的倾角。但该角度与实际阵元的安装位置有关,所以为固定值,可以在数据处理过程中直接代入计算。
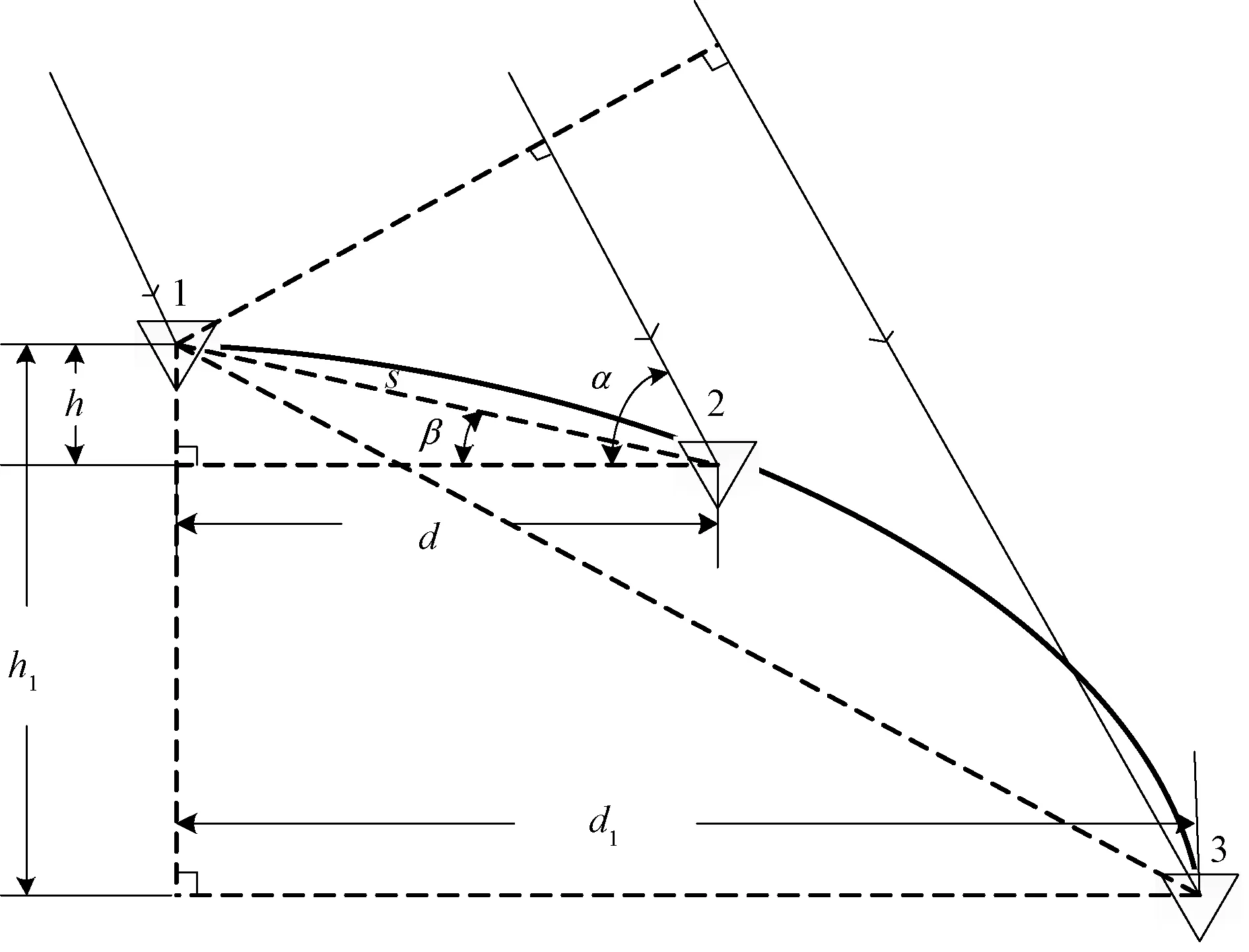
图4 天线安装示意图
依据上述定义,可以得到共形阵干涉仪各阵元与参考阵元之间的相位差公式:
(1)
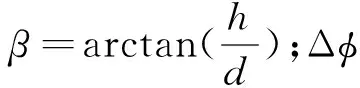
考虑到h为实际的高度差,当h与d相比很小时,对应的β值趋于0。于是上式与常见的干涉仪测向基本公式一致,可以采用常见的解模糊算法对此进行模糊数的确定,进而得到高精度的测向结果。然而若h与d可以比拟的时候,即β值不趋于0时,整个相差方程组不存在相同的正弦公因式;因而需要采用合适的解模糊算法,计算得到满足条件的模糊数,才能确定最终的测向结果。
先分析β值不趋于0时双基线的情况,且均为主瓣接收时(δ≈0),设2组基线长度分别为s1,s2,于是理论相位差如下式所示:
(2)
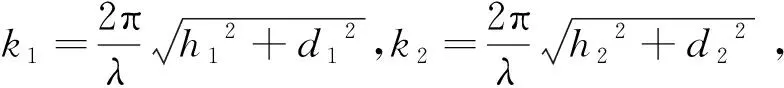
(3)
令m1=k1cosβ1,m2=k1sinβ1,n1=k2cosβ2,n2=k2sinβ2,前述变量均为已知量,可以通过测量计算直接获得,于是上式化简为:
(4)
依据cos2α+sin2α=1,可以得到k1,k2的关系:
(5)
依据基线长与模糊数之间的关系,针对双基线的情况,采取了二维搜索的方式,寻找最佳模糊数,标准为当某组模糊数(k1,k2)代入上述等式左侧得到的数值与1最接近,即判定该组模糊数即为所求,图5为遍历所有模糊数组合,得到的相关度与模糊数组的三维曲线图。

图5 二维搜索相关度曲线
从图5可以看出,在信噪比较高的情形下,相关系数呈单调变化,不存在多个峰值的情况,单一峰值点明显且对应的角度精度较高。但是由于基线长、波长及最大模糊数三者之间的关系,当入射波频率较大时,最大模糊数呈正比例增加,搜索范围则呈二次方增长,即当入射波频率增加1倍,搜索范围变为4倍,搜索效率下降明显;所以根据相关度曲线的变化趋势,考虑摈弃逐点搜索的方式,而采取更为高效的变步长搜索方式,以满足测向实时性的要求。
测向结果表明存在明显的峰值点,即模糊数结果明确,测向精度较高,需进一步依据相关度曲线优化搜索区域,提高搜索效率。
3 初相位补偿
为了达到有效接收信号的目的,针对共形阵列各阵元的方向图指向不一致,考虑方向图校正的方法提高信号接收检测效果,进而更加高效地提取相位信息。关于上述校正主要包含幅度校正与极化校正,是指按规定的方向图要求用一种或几种方法优化影响天线辐射特性的因素,使该天线系统产生的方向图满足指标要求[5-6]。
共形天线的形状要求大于其对于电磁特性的要求,所以其重构不仅仅局限于频率重构、方向图重构及极化重构等方面,还需重点讨论天线位置的重构问题。其中不免涉及到天线安装所带来的偏心偏轴影响,无论是偏心还是偏轴,对于侦察测向都会造成影响,会在一定程度上影响最后的测向结果。在“失之毫厘,谬以千里”的远程信息战时代,高精度测向是重要的前提条件之一。
位置校正一般是指天线阵列中的各个阵元位于同一平面,与载体平面表面的形状没有太大的关系。然而对于曲面阵列而言,天线单元需要与载体平台共面,即这个阵列是非平面形式,这势必增加了利用整体信号分析目标源的难度。其中一种重要的思想就是降维,需要将二维平面的天线阵元等效为一维阵列(即平面阵),从而可以利用平面阵列成熟的分析工具与方法对来波信号进行分析测向,提高分析结果的精度与可靠性。
根据天线的形式,大致可以分为2种情况对初始相位误差进行考虑。其一,全向天线,若不存在偏心误差时,天线相位方向图等相位(即从任意角度进入天线波瓣的信号附加的初始相位一致),当采用比相法测向时无需进行初始相位补偿;若存在偏心误差时,需要依据测得的角度与偏心误差之间的关系,对测向结果进行修正。其二,定向天线,同样若不存在偏心误差,位于天线幅度方向图主瓣以内的入射信号,引起的初始相位差几乎一致,只是在边界点处略有降低,一致性较强,如图6所示。然而当有信号从主瓣外区域进入天线时,所引起的相位变化与主瓣内的情况大不相同,后期进行补偿时较为困难;同全向天线一样若存在偏心误差时,需要依据测得的角度与偏心误差之间的关系,对测向结果进行修正。
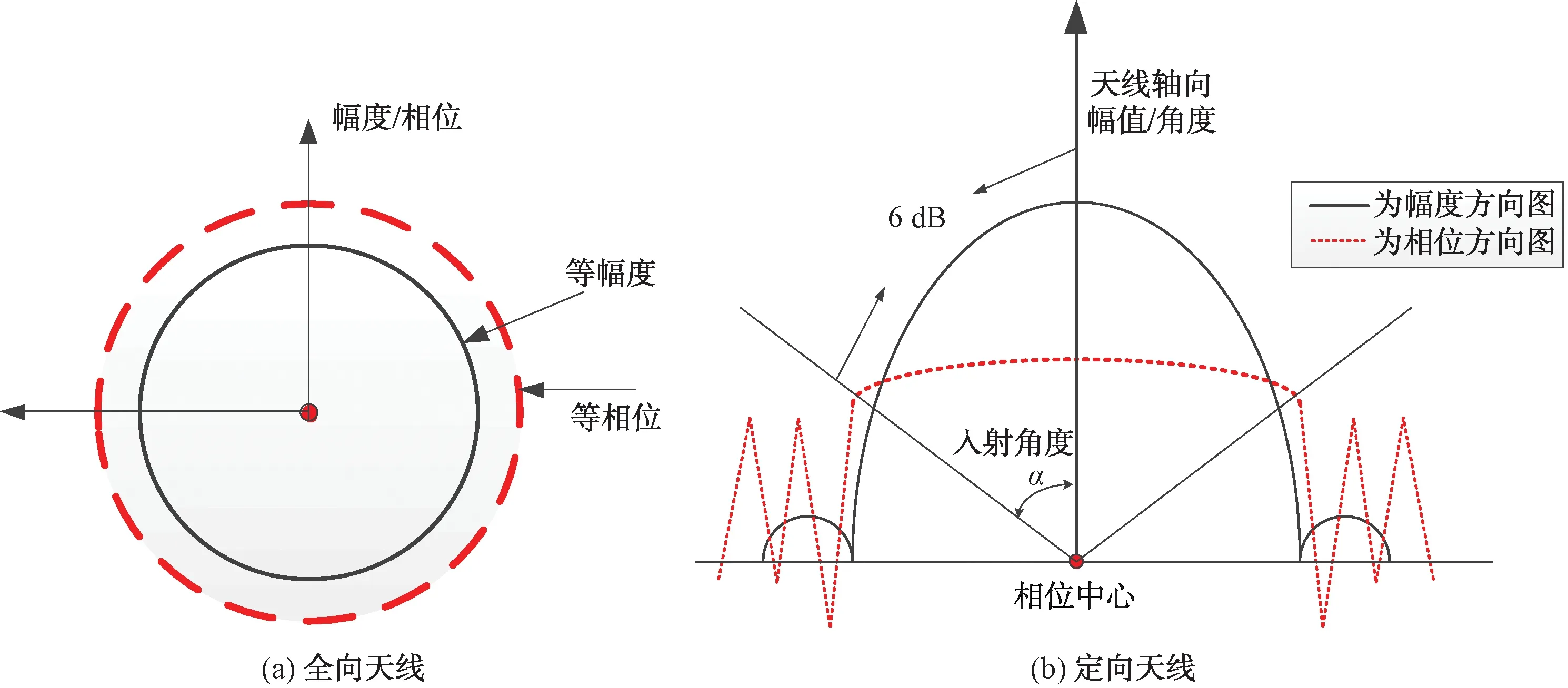
图6 全向天线和定向天线方向图示意图
由上面的讨论可知,虽然全向天线360°等相位面,当无偏心误差时,从任意方向入射无需进行初始相位补偿,数据处理方便但是增益较低无法实现远距离侦察。
然而对于定向天线而言,性能指标若能达到宽开大角度覆盖,根据共形平面调整天线主瓣覆盖范围,使得入射信号都能从主瓣区域接收,同样无需初相位补偿,而且其高增益能实现远距离侦收。全向天线和定向天线方向图如图6所示。
除了天线方向图会对接收信号的相位造成影响,天线位置是否安装准确也会对测向精度造成影响。其中主要涉及到2点,分别是偏心(安装位置偏离设定位置)和偏轴(天线安装偏离载机轴向),消除偏心偏轴所带来的影响能够进一步提高测向精度,达到测向指标要求。
图7给出了存在偏心偏轴天线安装的示意图。其中T为待测目标,O为载机位置,C为偏心点,由于天线安装偏离载机中心所致,偏心距离为OC(图中用d表示)。目标与载机的距离为OT(图中用S表示)。
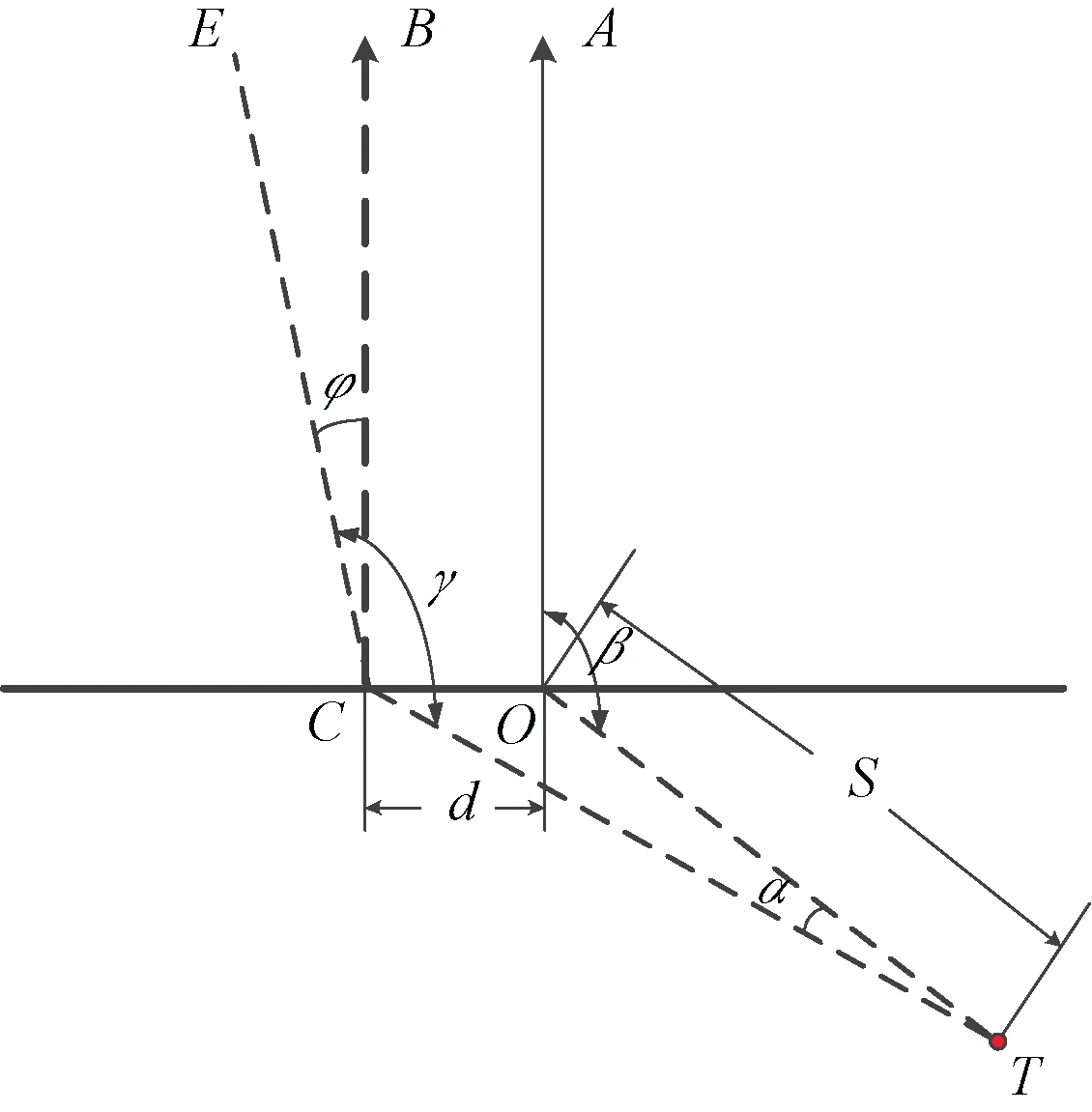
图7 偏心偏轴天线安装示意图
在图7坐标系中,目标相对于载机的初始角度为β,存在偏心偏轴误差后的角度变为γ,偏心角度为α,偏轴角度即天线安装偏离载机轴向的固定误差为φ。通过图中的几何关系可以得到上述4个角度的关系式:
(6)
可以分下述几种情况进行讨论:
(1) 当同时不存在偏心偏轴现象时,即α=φ=0°时,存在的测向误差主要是由于通道间的不平衡所引起的,同属于固有误差,应尽量消除该误差,进而提高测向的准确度。
(2) 当偏轴误差为0,仅存在偏心误差时,偏心误差的变化规律可以由下式给出:
α=arcsin(d/s·cosγ)
(7)
偏心误差曲线为反正弦函数,其数值主要取决于天线的偏心距离。
计算误差绝对值在1°左右,对于高要求、高精度测向而言误差较大,所以必须提高安装精度,修正测向结果,以保证测向结果的有效性及测向的高精度性。
同时依据测角精度分析误差公式:
(8)
通常在测向期间,往往会忽视阵元间距所带来的瞬变因素,但是通过上述分析可以得到在某些情形下带来的测向影响是不容忽视的,特别是在共形阵测向时,天线阵元都是安装在载体的曲面之上,更加容易引入孔径误差,所以需考虑间距误差造成的影响。先将上式变形可以得到:
(9)
式中:Δφ为干涉仪相位测量误差,主要包含信道相位失衡误差、接收机内部噪声引起的相位测量偏差(即相位噪声)、数字量化误差及同时到达干扰信号引起的相位偏差等共同表征,由于彼此间的独立性,可以线性叠加确定相位测量误差。
现主要考虑由于偏心造成的测向误差(即上式等号右侧第3项),它不仅与基线长度(阵元间距)有关,也同入射角度有关,于是将式(7)修正为:
(10)
将式(6)代入上式可以得到:
(11)
上式为关于变量α的隐函数,现定量分析偏心误差α随实测角度的变化规律。仿真了距离为10 m,偏心距离分别为0.1 m、0.2 m、0.3 m时的变化曲线,如图8所示。
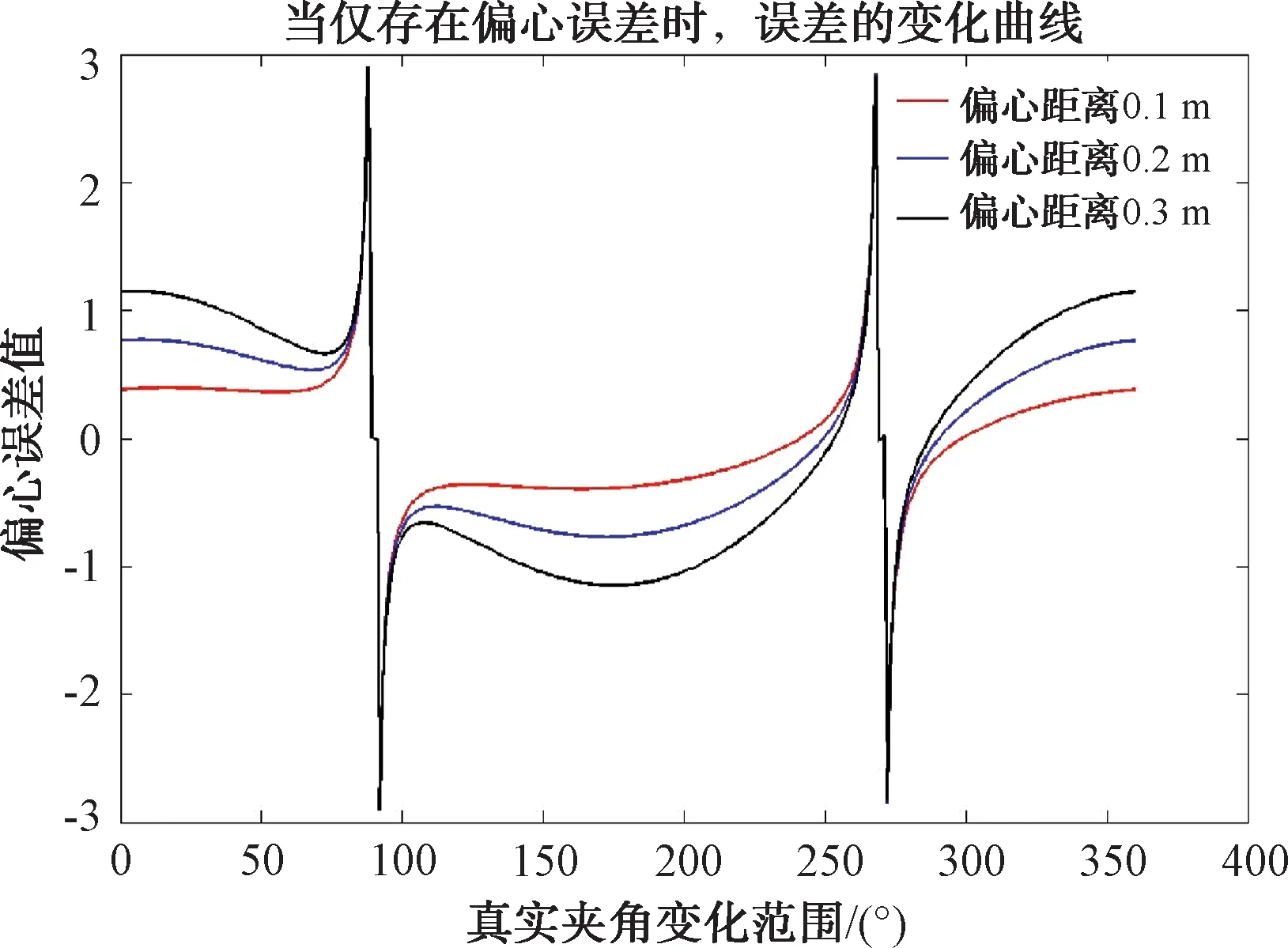
图8 偏心误差随入射角度变化修正曲线
从图8中可以看出,当辐射源到达角接近天线基线时,测角误差很大,这是由于路径差接近或达到峰值时,模糊数增加,导致测向结果变差。
(3) 当不存在偏心误差,仅存在偏轴误差时,该角度为固定值,不会随入射角度值发生变化,在实际测向时可以通过多次测试进行消除,以提高测向精度。
4 结束语
本文考虑了天线单元安装时的遮挡效应,采用降维的思想提高测向精度,通过对天线朝向的合理分配达到天线复用的效果,提高资源利用率;提出了二维复合搜索的方式,获取最佳模糊数进而解长基线模糊;同时考虑了阵元孔径误差的影响,修正了偏心误差的表达式。在减小目标RCS、提升载体气动性能的同时,为实现天线曲面共型方式的有效测向提供了方法。
