基于WOA–BP神经网络的液滴铺展预测

伍星，陈小勇，伍鹏飞，徐泽华，谢艳艳

基于WOA–BP神经网络的液滴铺展预测

伍星1a，陈小勇1,2，伍鹏飞1a，徐泽华1a，谢艳艳1a

（1.桂林电子科技大学 a.机电工程学院 b.电子信息材料与器件教育部工程研究中心，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004）

提高BP神经网络对电喷印过程中液滴铺展行为的预测能力。提出一种鲸鱼优化算法（WOA）优化BP神经网络的液滴铺展预测模型。首先，采用相场方法建立电场作用下液滴铺展的数值模型，并通过实验验证仿真结果的准确性。然后，选取初始直径、撞击速度、接触角和电场强度作为神经网络的输入参数，将最大铺展直径作为神经网络的输出参数，利用鲸鱼优化算法优化神经网络中的初始权值和阈值，构建液滴铺展预测模型。最后，基于仿真结果对预测模型进行训练与测试，并将其与传统的BP神经网络模型进行对比分析。相较于传统BP神经网络预测模型，WOA–BP神经网络预测模型的平均绝对误差、均方根误差分别降低了72.60%、77.60%，而平均绝对百分比误差则从15.029 3%减小为4.585 3%。WOA–BP神经网络预测模型可以更好地预测液滴铺展，可为液滴铺展的预测提供新的方法。

液滴；铺展；鲸鱼优化算法；BP神经网络；预测

电喷印技术是一种基于电流体动力学原理的新兴打印技术，其不仅能克服传统喷墨打印过程中容易出现喷嘴堵塞的缺点，还具有成型精度高、选材广泛[1]等优点，因而被广泛应用于光学器件、柔性电子等领域[2-3]。电喷印的打印效果除了会受锥射流形态[4]和喷嘴结构[5]影响外，还与液滴在基板上的铺展行为密切相关。因此，为了提高打印精度，对液滴铺展行为进行预测就显得尤为重要。由于实验条件的限制，现阶段学者们主要通过理论分析、经验公式以及数值模拟等方法对液滴铺展行为进行预测。

在理论分析方面，Lee等[6]改进了黏性耗散表达式，并推导出了最大铺展因子的预测公式。春江等[7]考虑到辅助耗散和重力势能的影响，修正了最大铺展直径的预测公式。在经验公式方面，李大树等[8]基于实验数据拟合得到了最大铺展系数与雷诺数之间的表达式。郝晓莹[9]运用最小二乘法得到了液滴撞击微柱表面时最大铺展直径与韦伯数、粒径、接触角和微结构高度之间的函数关系。在数值模拟方面，闫哲等[10]通过建立不同微结构下液滴铺展预测模型，发现液滴在三角沟槽表面的最大铺展因子最小。梁超等[11]基于VOF方法研究发现最大铺展系数与壁面的接触角有关。李培生等[12]基于LBM方法模拟了液滴铺展行为，研究发现高雷诺数下液滴更容易铺展。虽然上述方法都取得了一定的成果，但也存在着各自的不足。其中理论分析方法推导出的预测公式存在特定的适用范围，经验公式计算的结果往往与实验结果之间存在较大误差，而数值模拟方法虽然能得到较为精准的结果，但计算复杂且容易出现重复性建模的情况，需要耗费大量时间。

随着机器学习技术的发展，为解决液滴铺展这类受众多因素影响且内在关系复杂的非线性预测问题提供了一种新的思路。李光远[13]将BP神经网络用于预测液滴铺展过程中的能量变化。针对传统BP神经网络预测精度不高且收敛速度慢的问题，学者们采用了智能优化算法优化BP神经网络中的初始权值和阈值[14-16]。虽然改进后的BP神经网络在部分领域得到了应用，但将其用于电场作用下液滴铺展行为的预测研究还未见报道。

综上所述，本文采用鲸鱼优化算法优化BP神经网络，建立电场作用下液滴铺展预测模型，并通过实例验证了模型的预测性能。

1 数值模型与模型验证

1.1 控制方程

本文基于COMSOL Multiphysics软件，采用相场方法建立对应的数值模型。由于电场作用下液滴在铺展过程中主要受到重力、电场力、黏性力和表面张力的影响。因此，对应的Navier–Stokes方程和连续性方程[17]分别为：

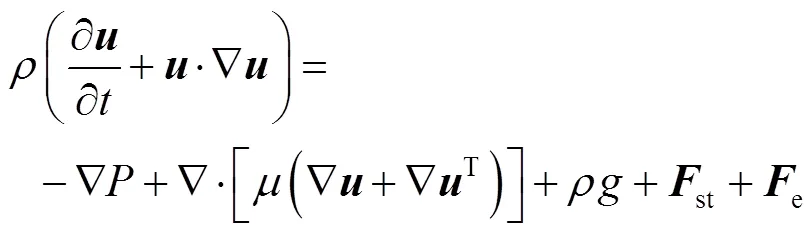
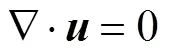
式中：为液滴密度；为液滴速度矢量；为液滴黏度；st为单位体积界面张力矢量；e为电场力矢量。

在相场中，Cahn-Hilliard方程可以表示为：

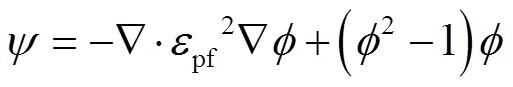
液滴受到电场力可由麦克斯韦应力张量表示为：

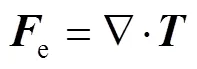
由于流体不可压缩，故麦克斯韦应力张量为：

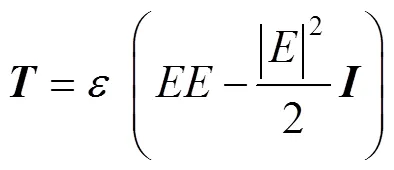
式中：为外加电场；为介电常数；为单位矩阵。

1.2 动态接触角模型

接触角作为表征基板润湿性的重要参数，对其设置不当将直接影响仿真结果的准确性。目前，接触角的设置方式主要分为静态接触角模型和动态接触角模型。其中静态接触角模型认为液滴运动过程中接触角始终是一个定值，该模型虽然设置简单，但模拟结果并不理想。动态接触角模型由于考虑了毛细数对接触角的影响，能更真实地模拟出液滴撞击基板的过程[18-20]。本文选用Kistler动态接触角模型，对应的动态接触角d可表示为：

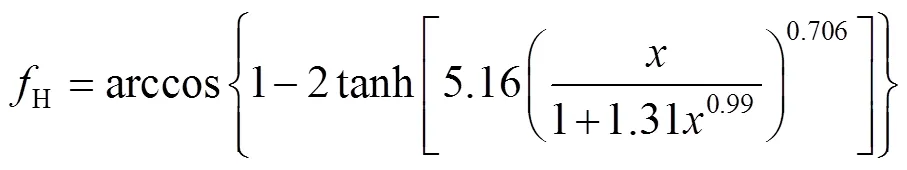
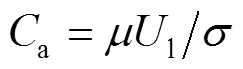
式中：a为毛细数；l为接触线速度；为界面张力系数。

1.3 模型验证

为了验证数值模型的可行性，在相同工况下：液滴初始直径为3 mm、电场强度为6.5 kV/cm、撞击速度为0.766 m/s，与文献[21]的实验结果进行对比。由图1可知，该模型能较好地模拟不同时刻液滴铺展的形态演化过程且仿真得到的铺展因子与实验值之间误差较小。说明该模型用于研究电场作用下液滴铺展行为是可行的，可以为后续WOA–BP神经网络模型的训练与效果验证提供样本数据。

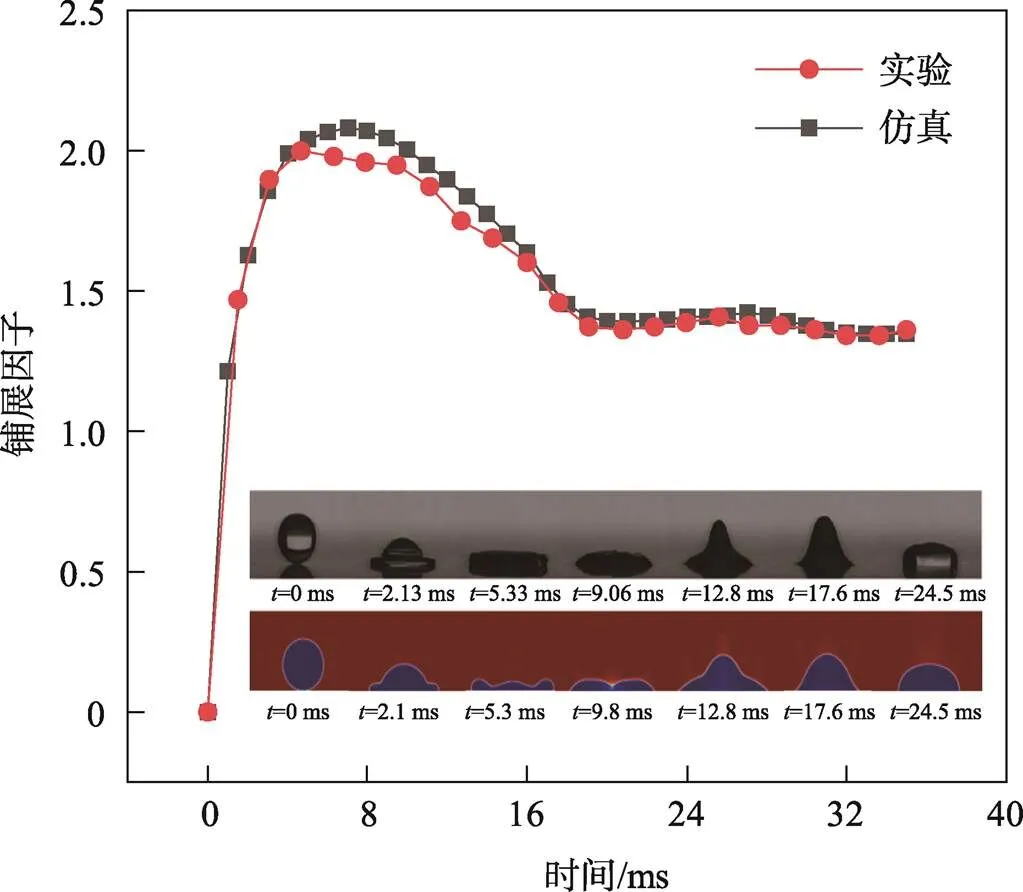
图1 电场作用下液滴铺展行为实验与仿真对比

2 构建WOA–BP神经网络预测模型

2.1 BP神经网络

BP神经网络是一种以信息前向传递，误差反向传播为主要特点的多层前馈神经网络。其网络结构包括输入层、隐含层和输出层[22]。在信息前向传递过程中，输入信号依次通过输入层、隐含层，最终到达输出层。当输出结果与期望结果之间的误差不满足预设的学习精度时，不断更新网络中不同层与层之间的连接权值以及隐含层、输出层的阈值的过程，称为误差的反向传播。

BP神经网络模型的预测精度除了受权值和阈值的影响外，还受到网络中隐含层节点数的制约[23]。如果隐含层节点数过少，会造成BP神经网络的预测精度偏低，但是隐含层节点数过多，又容易出现过拟合现象。通常隐含层节点数的确定方法如下：先根据经验公式[24]得到隐含层节点数的取值范围，再分别计算不同隐含层节点数下的训练集均方误差，将训练集均方误差最小时所对应的隐含层节点数确定为最佳隐含层节点数。具体公式见式（10）。

式中：为输入层节点数；为输出层节点数；为[1,10]之间的任意整数；为隐含层节点数。

2.2 鲸鱼优化算法

鲸鱼优化算法（Whale Optimization Algorithm，WOA）是一种通过模拟座头鲸的狩猎行为而衍生出的智能优化算法[25]。在狩猎过程中，座头鲸会成群包围猎物，随后在螺旋向上运动的同时，吐出大量气泡形成气泡网将猎物包围并驱赶至气泡网中心，最后吞食猎物。座头鲸狩猎行为如图2所示。

图2 座头鲸的狩猎行为[25]

WOA算法的核心就是用数学模型描述座头鲸包围猎物、气泡网攻击和搜索猎物这3种行为。

1）包围猎物。在包围猎物阶段，先将最靠近猎物的鲸鱼定义为最佳鲸鱼，然后其他鲸鱼根据最佳鲸鱼的位置更新自身的位置，从而实现对猎物的包围。此过程对应的数学公式见式（11）。

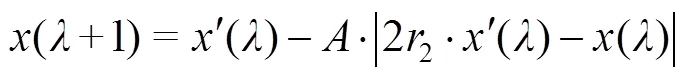
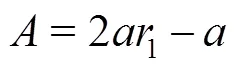
2）气泡网攻击。进入气泡网攻击阶段后，座头鲸不仅会进一步收缩包围圈，还会螺旋上升游向猎物。假设选择这2种行为的概率是相同的，根据式（13）计算出更新后鲸鱼的位置。

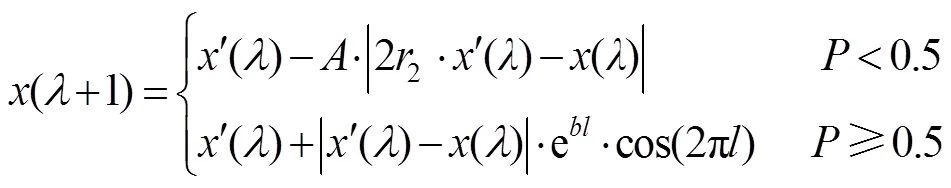
式中：为对数螺旋形状常量；为[−1,1]之间的随机数。

3）搜索猎物。在搜索猎物阶段，鲸鱼会随机从种群中选择一条鲸鱼靠近，以此提高鲸鱼群体的全局搜索能力。此过程对应的数学公式见式（14）。

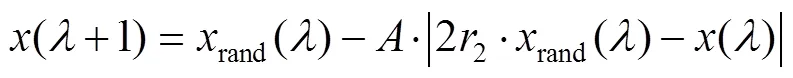
2.3 WOA–BP神经网络模型

由于传统BP神经网络中的初始权值和阈值具有随机性，使得算法容易收敛于局部最优点，从而影响最终的预测效果[26]。为解决上述问题，本文利用WOA算法对BP神经网络进行改进。具体流程如下。

1）采集数值模型得到的数据，划分数据集，并进行归一化处理。

2）BP神经网络初始化，设置训练次数、学习速率和学习精度，并确定神经网络结构。

3）初始化WOA参数，将训练样本与测试样本的均方误差作为适应度函数。

4）计算鲸鱼的适应度值，记录最佳个体位置。

5）更新参数、、、。

7）判断是否满足终止条件。若达到最大迭代次数，则输出最优的初始权值和阈值。否则重复执行步骤（4）—（7）。

8）将最优的初始权值和阈值带回神经网络。

9）计算BP神经网络的输出误差。

10）判断是否满足终止条件。若输出误差达到预设的学习精度或最大训练次数，经反归一化处理后，即可输出预测结果。否则先更新权值和阈值，然后重复执行步骤（9）—（10）。

WOA算法改进BP神经网络的流程如图3所示。

3 实例分析

3.1 数据获取与归一化处理

采用上文所建立的数值模型获取初始直径（2、2.5、3 mm）、撞击速度（0.5、0.6、0.7 m/s）、接触角e（67°、155°）和电场强度（4.5、5.5、6.5 kV/cm）不同组合条件下的最大铺展直径，共计30组样本数据。从中随机选择21组数据作为训练样本，剩余9组数据作为测试样本。

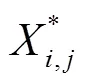
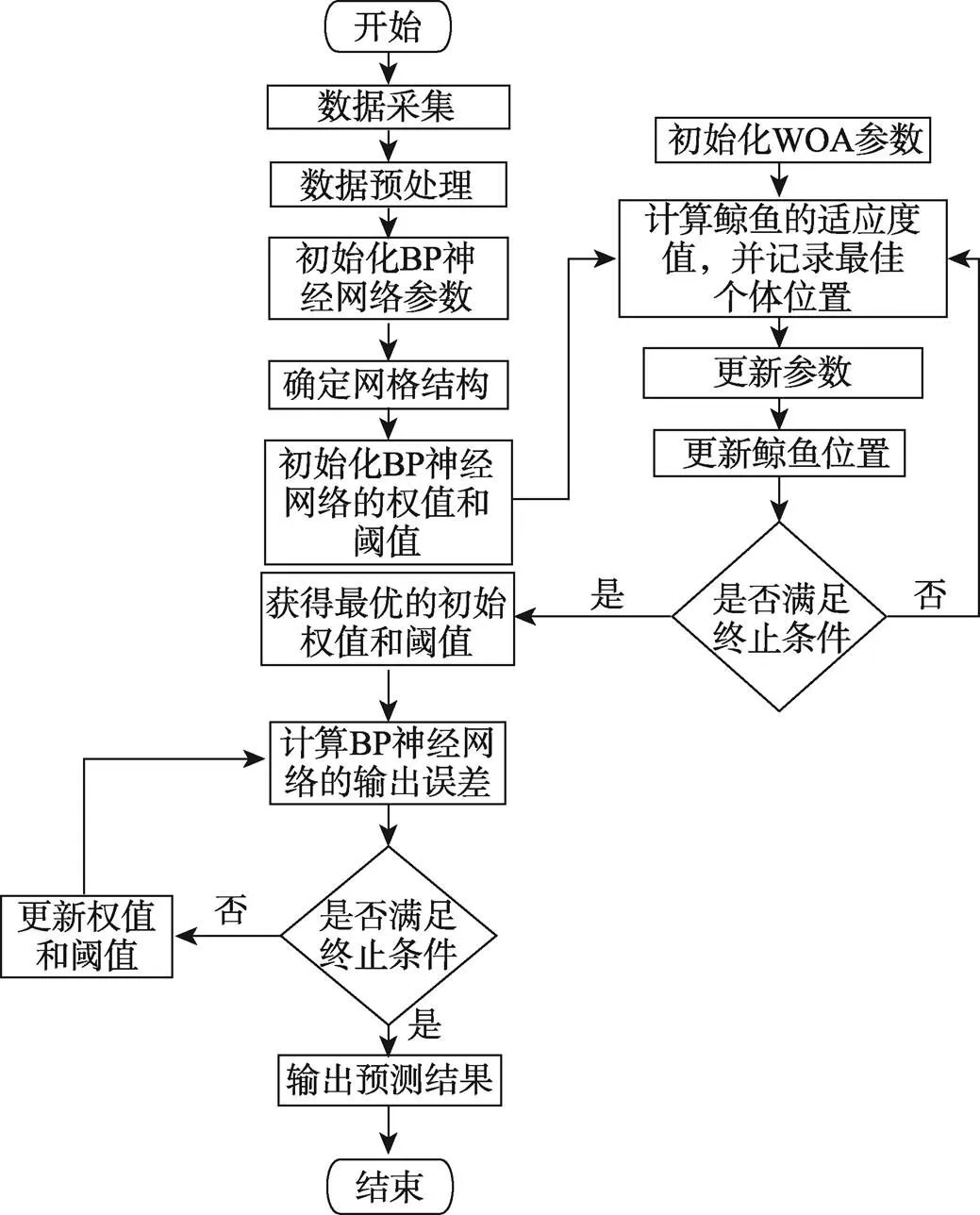
图3 WOA算法改进BP神经网络的流程

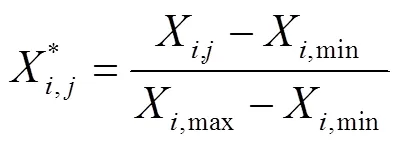
式中：X为第个因素中第组的输入值；Xmin为第个因素所对应的输入序列中的最小值；Xmax为第个因素所对应的输入序列中的最大值。

对原始输出数据也进行类似处理：

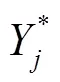
3.2 神经网络结构的确定

由前文可知，BP神经网络的输入层参数为4，BP神经网络的输出层参数为1。综合考虑训练时间和网络精度后，选择单隐含层结构。由式（10）计算得到隐含层节点数的取值范围为[3,12]。在BP神经网络中设置训练次数为1 000，学习速率为0.01，学习精度为0.000 001，使用Matlab软件进行仿真，得到不同隐含层节点数对应的训练集均方误差如图4所示。从图4中可以看出，当隐含层节点数为8时，对应的训练集均方误差最小。故最佳隐含层节点数为8。

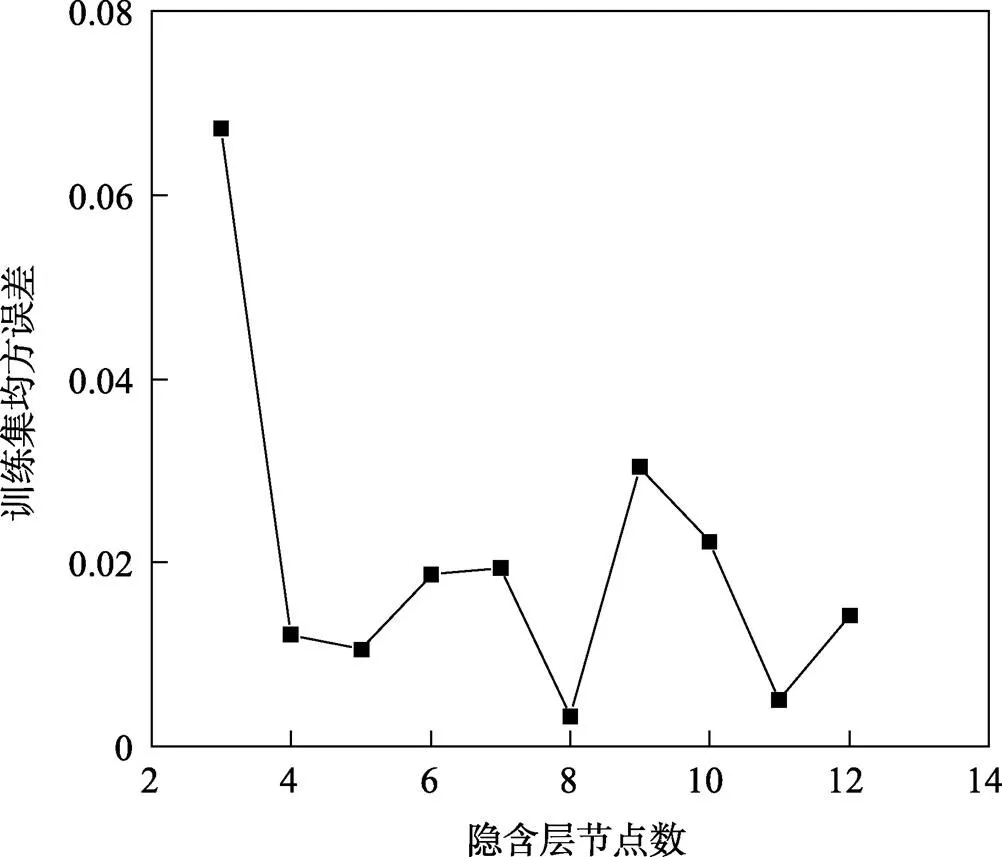
图4 不同隐含层节点数对应的训练集均方误差

对应的BP神经网络结构如图5所示。

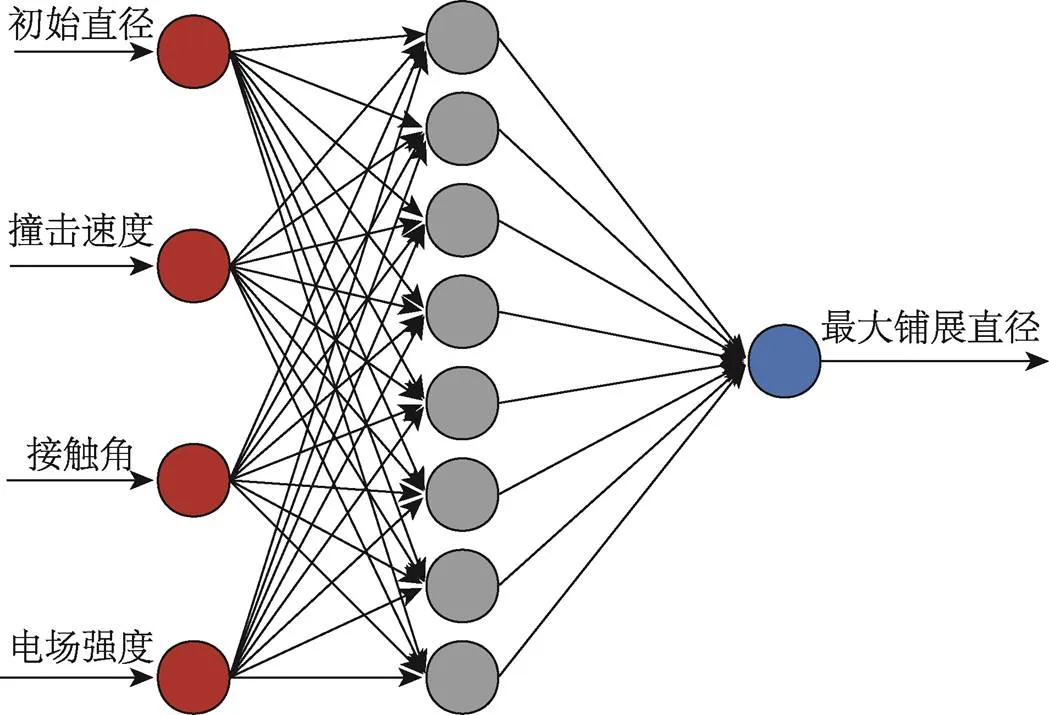
图5 BP神经网络结构

3.3 预测结果与评价

在WOA算法中，将种群规模设置为30，迭代次数设置为50，建立液滴铺展预测模型。将样本数据导入模型，得到的适应度值变化曲线如图6所示。由图6可知，在迭代次数增大初期，适应度值逐渐减小。经过大约14次迭代后，适应度值不再变化。

真实值与不同模型得到的预测值对比如图7所示。从图7可以看出，在绝大多数测试样本中，使用WOA–BP模型得到的预测结果更接近真实值。

为了能更客观地比较BP神经网络预测模型和WOA–BP预测模型对液滴铺展的预测效果，选取平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）等指标对模型的预测性能进行评价，各评指标的计算式见式（17）‒（19）。各评价指标的计算结果如表1所示。

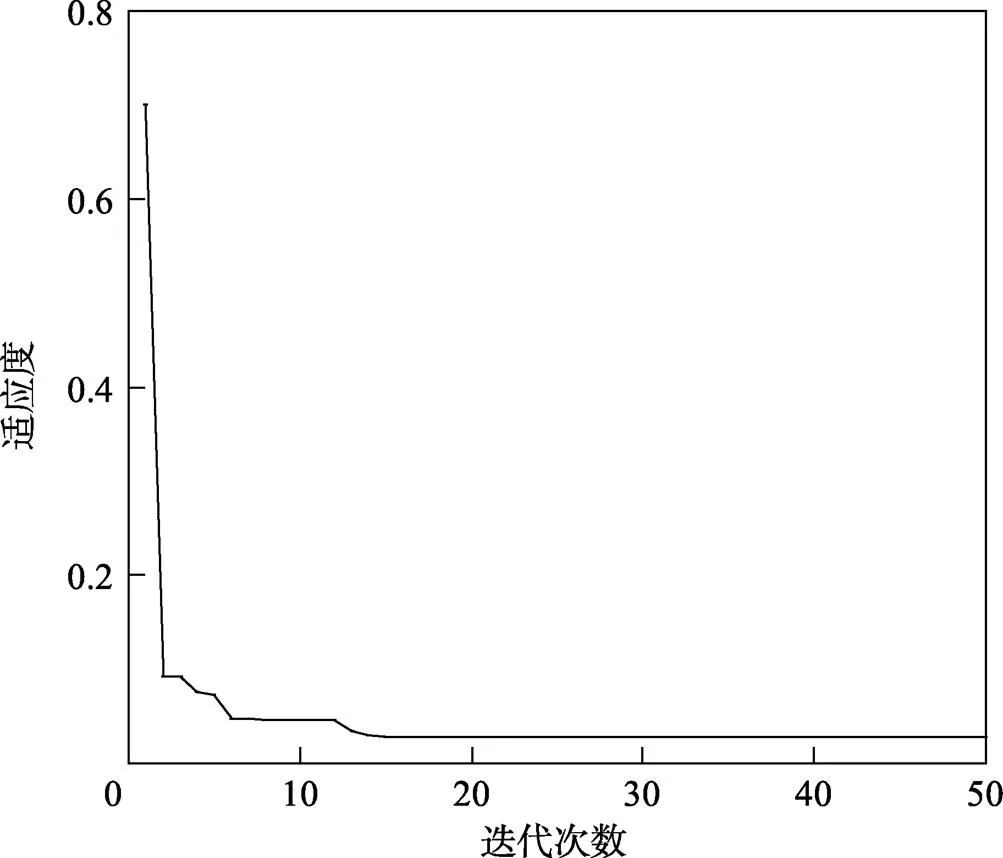
图6 适应度值变化曲线

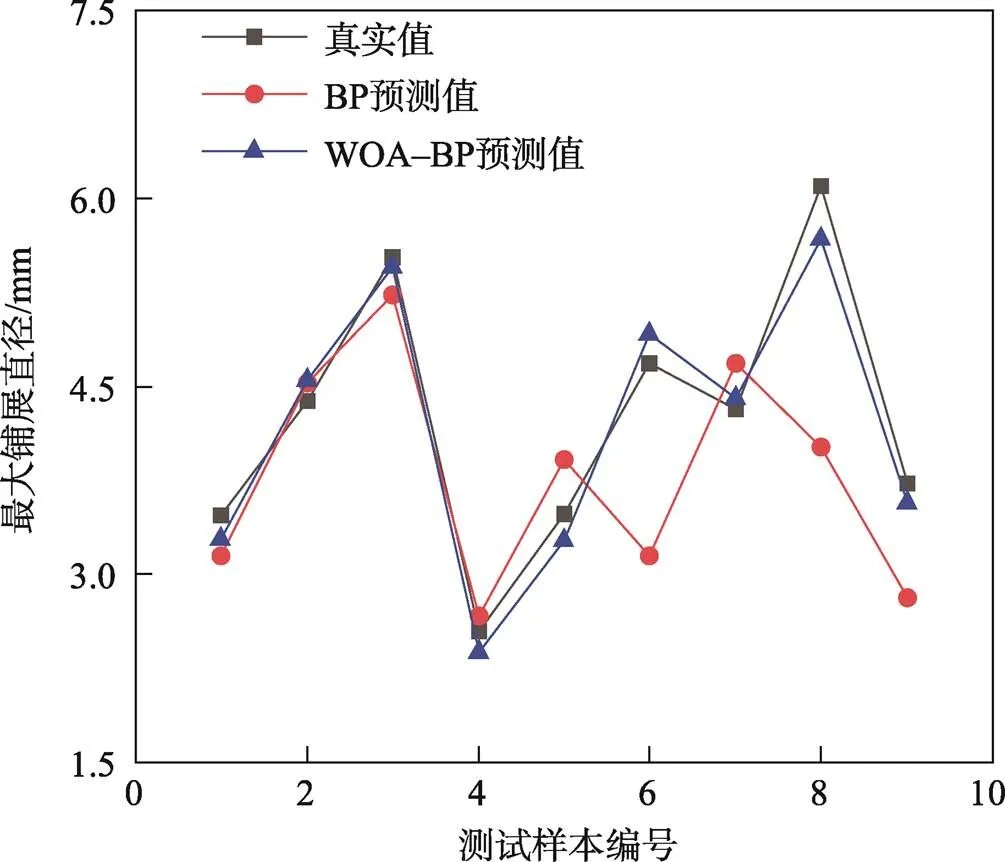
图7 真实值与不同模型得到的预测值对比

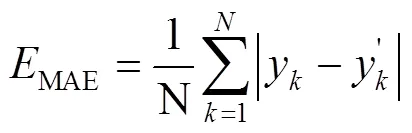
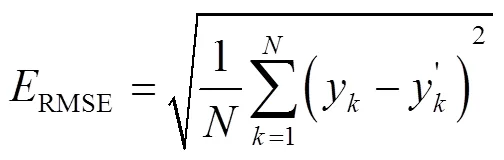
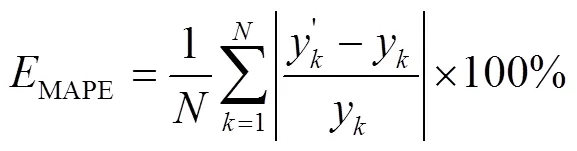
表1 优化前后模型的预测效果评价

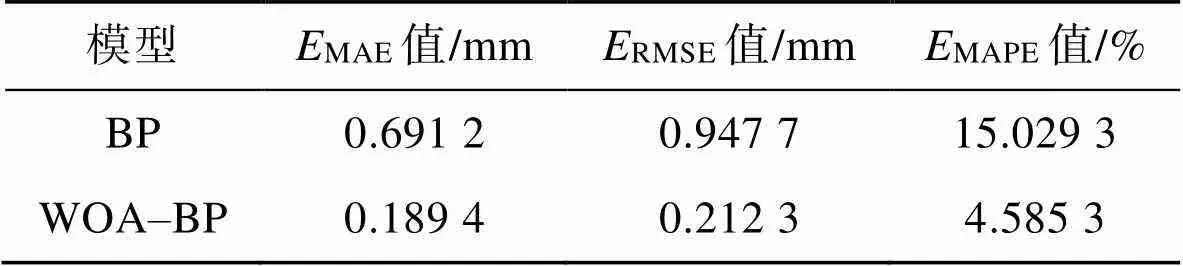
Tab.1 Evaluation of the prediction effect of the model before and after optimization

由表1可知，与传统BP神经网络预测模型相比，WOA–BP预测模型的平均绝对误差减小了72.60%，均方根误差减小了77.60%，平均绝对百分比误差也从15.029 3%减小为了4.585 3%。由此可见，将鲸鱼优化算法与BP神经网络相结合后，能显著提高模型对液滴铺展的预测能力，有助于研究液滴铺展的内在机理。通过控制液滴在基板上的铺展行为，可以对打印图案的几何形貌和位置精度进行调控，从而实现柔性电子、光学器件的高精度打印。

4 结语

本文将鲸鱼优化算法与BP神经网络相结合，建立了电场作用下液滴铺展预测模型。相较于传统BP神经网络预测模型，WOA–BP神经网络预测模型的平均绝对误差、均方根误差以及平均绝对百分比误差都大幅减小。证明了引入鲸鱼优化算法可以避免BP神经网络算法因陷入局部最优点而出现预测精度偏低的情况。运用该模型可以对液滴铺展行为进行快速精准地预测，有助于研究液滴铺展的内在机理，可为提高电喷印的打印效果提供理论基础。

[1] QU Xiao-li, XIA Peng, HE Jian-kang, et al. Microscale Electrohydrodynamic Printing of Biomimetic PCL/nHA Composite Scaffolds for Bone Tissue Engineering[J]. Materials Letters, 2016(185): 554-557.

[2] AN H S, PARK Y G, KIM K, et al. High-Resolution 3D Printing of Freeform, Transparent Displays in Ambient Air[J]. Advanced Science, 2019, 6(23): 1901603.

[3] IM H G, AN B W, JIN J, et al. A High-Performance, Flexible and Robust Metal Nanotrough-Embedded Transparent Conducting Film for Wearable Touch Screen Panels[J]. Nanoscale, 2016, 8(7): 3916-3922.

[4] 王莎莎, 唐正宁, 缪斌鹰, 等. EHD喷印技术相关参数数值分析[J]. 包装工程, 2015, 36(7): 145-148.

WANG Sha-sha, TANG Zheng-ning, MIAO Bin-ying, et al. Numerical Analysis of the Relevant Parameters in EHD Micro-Jet Printing[J]. Packaging Engineering, 2015, 36(7): 145-148.

[5] ZHANG Lei. Characteristics of Drop-on-Demand Droplet Jetting with Effect of Altered Geometry of Printhead Nozzle[J]. Sensors and Actuators A: Physical, 2019, 298: 111591.

[6] LEE J B, DEROME D, GUYER R, et al. Modeling the Maximum Spreading of Liquid Droplets Impacting Wetting and Nonwetting Surfaces[J]. Langmuir: the ACS Journal of Surfaces and Colloids, 2016, 32(5): 1299-1308.

[7] 春江, 王瑾萱, 徐晨, 等. 液滴撞击超亲水表面的最大铺展直径预测模型[J]. 物理学报, 2021, 70(10):248-258.

CHUN Jiang, WANG Jin-xuan, XU Chen, et al. Theoretical Model of Maximum Spreading Diameter on Superhydrophilic Surfaces[J]. Acta Physica Sinica, 2021, 70(10): 248-258.

[8] 李大树, 仇性启, 于磊, 等. 液滴碰撞水平壁面实验研究[J]. 实验技术与管理, 2015, 32(4): 66-71.

LI Da-shu, QIU Xing-qi, YU Lei, et al. Research on Experiments of Droplet Impacting on a Flat Surface[J]. Experimental Technology and Management, 2015, 32(4): 66-71.

[9] 郝晓莹. 液滴撞击微结构表面的数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.

HAO Xiao-ying. Numerical Study of Droplet Impact on Microstructured Surfaces[D]. Harbin: Harbin Engineering University, 2021.

[10] 闫哲, 李艳, 李川, 等. 液滴撞击不同固体表面的数值模拟研究[J]. 热科学与技术, 2018, 17(1): 8-14.

YAN Zhe, LI Yan, LI Chuan, et al. Numerical Simulation Study of Droplet Impact on Various Solid Surface[J]. Journal of Thermal Science and Technology, 2018, 17(1): 8-14.

[11] 梁超, 王宏, 朱恂, 等. 液滴撞击不同浸润性壁面动态过程的数值模拟[J]. 化工学报, 2013, 64(8): 2745-2751.

LIANG Chao, WANG Hong, ZHU Xun, et al. Numerical Simulation of Droplet Impact on Surfaces with Different Wettability[J]. CIESC Journal, 2013, 64(8): 2745-2751.

[12] 李培生, 李志豪, 黄逸宸, 等. 基于LBM伪势模型下的三维大密度液滴撞击壁面数值研究[J]. 水动力学研究与进展(A辑), 2020, 35(4): 532-540.

LI Pei-sheng, LI Zhi-hao, HUANG Yi-chen, et al. Numerical Study of Three-Dimensional Large Density Ratio Droplet Impact Wall Surface Based on LBM Pseudopotential Model[J]. Chinese Journal of Hydrodynamics, 2020, 35(4): 532-540.

[13] 李光远. 液滴撞击壁面铺展流动特性的数值模拟及预测研究[D]. 乌鲁木齐: 新疆大学, 2021.

LI Guang-yuan. Numerical Simulation and Prediction of Flow Characteristics of Droplet Impacting on the Wall[D]. Urumqi: Xinjiang University, 2021.

[14] CHENG Peng-peng, CHEN Dao-ling, WANG Jian-ping. Clustering of the Body Shape of the Adult Male by Using Principal Component Analysis and Genetic Algorithm–BP Neural Network[J]. Soft Computing, 2020, 24(17): 13219-13237.

[15] HUANG Li-bin, JIANG Lin, ZHAO Li-ye, et al. Temperature Compensation Method Based on an Improved Firefly Algorithm Optimized Backpropagation Neural Network for Micromachined Silicon Resonant Accelerometers[J]. Micromachines, 2022, 13(7): 1054.

[16] HUANG Yu-an, XIANG Yu-xing, ZHAO Rui-xiao, et al. Air Quality Prediction Using Improved PSO-BP Neural Network[J]. Ieee Access, 2020, 8: 99346-99353.

[17] TIAN Ye, WANG Hong, ZHOU Xin, et al. A Combined Experimental and Numerical Study on Droplet-Impact Induced Breakup and Ejection Behaviors in Vertical Electric Field[J]. Chemical Engineering Science, 2021, 239: 116636.

[18] BRACKE M, VOEGHT F D, JOOS P. The Kinetics of Wetting: the Dynamic Contact Angle[J]. Trends in Colloid and Interface Science Ⅲ, 1989: 142-149.

[19] KISTLER S F. Hydrodynamics of Wetting[J]. Wettability, 1993, 6: 311-430.

[20] 周鑫, 马小晶, 胡丽娜, 等. 不同壁面条件下液滴撞击铺展特性的模拟研究[J]. 计算力学学报, 2022, 39(6): 761-767.

ZHOU Xin, MA Xiao-jing, HU Li-na, et al. Simulation Study of Droplet Impact Spreading Characteristics under Different Wall Conditions[J]. Journal of Computational Mechanics, 2022, 39(6): 761-767.

[21] 李英杰. 电场下液滴撞击过冷壁面的数值模拟研究[D]. 重庆: 重庆大学, 2021.

LI Ying-jie. Numerical Simulation Study on Droplet Impacting Supercooled Wall under Electric Field[D]. Chongqing: Chongqing University, 2021.

[22] DING Shi-fei, SU Chun-yang, YU Jun-zhao. An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm[J]. Artificial intelligence review, 2011, 36(2): 153-162.

[23] 王毅红, 张建雄, 兰官奇, 等. 压制生土砖强度的人工神经网络预测模型[J]. 华南理工大学学报(自然科学版), 2020, 48(7): 115-121.

WANG Yi-hong, ZHANG Jian-xiong, LAN Guan-qi, et al. Artificial Neural Network Prediction Model for Compressive Strength of Compacted Earth Blocks[J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(7): 115-121.

[24] 曹杨, 王红红, 林超, 等. 海底管道清管器运行时间预测[J]. 油气储运, 2022, 41(4): 451-457.

CAO Yang, WANG Hong-hong, LIN Chao, et al. Prediction on Running Time of Pigs in Submarine Pipelines[J]. Oil & Gas Storage and Transportation, 2022, 41(4): 451-457.

[25] MIRJALILI S, LEWIS A, et al. The Whale Optimization Algorithm[J]. Advances in engineering software, 2016, 95: 51-67.

[26] 董江涛, 杜震宇. 基于GA‒BP神经网络的土壤‒空气换热器换热量预测分析[J]. 可再生能源, 2021, 39(3): 307-314.

DONG Jiang-tao, DU Zhen-yu. Heat Exchange Quantity Prediction of Earth-Air Heat Exchanger Based on GA-BP Neural Network[J]. Renewable Energy Resources, 2021, 39(3): 307-314.

Droplet Spreading Prediction Based on WOA-BP Neural Network

WU Xing1a, CHEN Xiao-yong1,2, WU Peng-fei1a, XU Ze-hua1a, XIE Yan-yan1a

(1. a. School of Mechatronics Engineering b. Engineering Research Center of Electronic Information Materials and Devices, Ministry of Education, Guilin University of Electronic Technology, Guangxi Guilin 541004, China; 2. Guangxi Key Laboratory of Manufacturing System and Advanced Manufacturing Technology, Guangxi Guilin 541004, China)

The work aims to improve the prediction ability of BP neural network for droplet spreading behavior during electrojet printing. A whale optimization algorithm (WOA) was proposed to optimize the droplet spreading prediction model based on BP neural network. Firstly, the numerical model of droplet spreading under the action of electric field was established by the phase field method, and the accuracy of the simulation results was verified by experiments. Then, the initial diameter, impact velocity, contact angle and electric field strength were selected as input parameters for the neural network, the maximum spreading diameter was taken as the output parameter of the neural network, and the initial weights and thresholds in the neural network were optimized by the whale optimization algorithm to construct the droplet spreading prediction model. Finally, the prediction model was trained and tested based on the simulation results, and was compared and analyzed with the traditional BP neural network model. Compared with the traditional BP neural network prediction model, the mean absolute error and root mean square error of the WOA-BP neural network prediction model were reduced by 72.60% and 77.60% respectively, while the mean absolute percentage error was reduced from 15.029 3% to 4.585 3%. It is demonstrated that the WOA-BP neural network prediction model can better predict the droplet spreading and can provide a new method for the prediction of droplet spreading.

droplet; spreading; whale optimization algorithm; BP neural network; prediction

TP183；O35

A

1001-3563(2023)13-0181-07

10.19554/j.cnki.1001-3563.2023.13.022

2022−11−02

广西自然科学基金（2022GXNSFAA035616）；广西制造系统与先进制造技术重点实验室基金（2006540007Z）；电子信息材料与器件教育部工程研究中心（EIMD–AB202008）

伍星（1994—），男，硕士生，主攻微纳电子制造工艺。

陈小勇（1984—），男，博士，高级实验师，主要研究方向为微纳电子制造工艺及流动控制技术。

责任编辑：曾钰婵