基于量子增强的光学测量技术综述

王 曼,王惠林,李 皓,孟合民,马昀楷,高泽东,王 律,王希骋,程洪亮

(1.西安应用光学研究所,西安 710065;2.中检西部检测有限公司,西安 710032;3.西安现代控制技术研究所,西安 710065)

1 引言

量子光学是研究光的量子特性和现象及其与物质相互作用的物理学领域[1]。计量学是测量及其应用的科学[2]。在电磁场绘景下,光场由于良好的可操作性,与外场的频率、相位等信息表现出较强的耦合特性[3]。因此,计量学领域常引入光子探针,用于间接的表征功率、极化率、磁场强度、时间等各类物理信息[4-7],并引发了非线性光学、量子标准、量子计算、量子通信等领域的爆发性拓展。

当采用经典光场进行探测,其精度受到不确定性原理(Uncertainty Principle,测量导致被测系统产生扰动)和散射噪声(Shot Noise)的基本限制,随着测量次数N的增加,测量不确定度的极限正比于减少,称之为标准量子极限(Standard Quantum Limit,SQL)。通过引入压缩态(Squeezed state)、相干态(Coherent state)等技术,可以将测量极限进一步压缩,得到正比于1/N的海森堡极限(Heisenberg Limit,HL)。当前的实验指出了量子增强的光学计量技术的出发点:利用光的量子效应来提高测量精度,超越SQL。

量子光学增强的计量技术已经在引力探测、量子计算、频率基准、微弱电磁场测量等多个领域表现出应用潜力。但是这些实验性工作的研究脉络是什么? 下一步如何进一步提升测量精度? 仪器科学领域应进行哪些预先研究工作以适应量子光学的未来?

为回答上述问题,通过介绍该领域的基础概念、实验过程和实验结果,回顾与计量学相关的量子光学基本工具和技术,描述实现量子增强光学测量的主要协议和策略,并总结该领域的主要实验成果和突破。对当前的研究现状进行展望,提出为推动量子光学计量技术,未来仪器领域应重点发展的重点方向。

2 测量精度的下界-克拉美罗界

具体而言,量子增强光学计量技术的指利用非经典光源进行测量的技术。量子计量领域的早期综述性工作可参见赵克功[8-10]、陈竹年[11]等人的综述,在此主要介绍量子增强对光学计量技术的突破,也就是对SQL 的突破。简单来讲,首先可以确定这样的一副物理绘景:由于海森堡不确定性原理,在对一对相关的物理量进行测试时,总是不能同时的缩小他们的不确定度。由此,科学家们引入了另外两种思路[12]:一种称为量子非破坏性测量(quantum non demolition measurement,QND),引入与待测系统对易的耦合算子(辅助的耦合系统),此时对耦合系统进行测量不会导致测量过程对待测系统的破坏。另一种技术为量子增强的测量技术,通过牺牲互补分量的不确定度,实现对待测系统不确定度的压缩。

为了定量的描述测量值与真值的偏差,需要引入费雪信息(Fisher Information)的概念[13]。通过对感兴趣的物理量φ进行一系列测量,得到一系列的测量值Xi与初始的分布函数f(X;φ)。在此基础上,希望得到系统的最大似然函数(Maximum Likelihood Estimate,MLE),描述被测量的真值。为了量化与f(X;φ)的接近特性,需要引入期望和方差,即与,通常在零差估计情况下为:

通过计算对数似然函数的导数,即似然函数对数的曲率,可以定量的表述其尖锐特性为:

对其求期望得到费雪信息为:

引入柯西-施瓦茨不等式,可得:

不等号右边第一个括号中的因子给出待测参数φ的方差,第二个括号中的因子给出费雪信息。从式(4)可以得到:

式(5)约束了测量方差的下边界,被称为克拉美罗界(Cramér-Rao bound,CRB)。测量方差直接取决于系统费雪信息的大小,当F(φ)与测量次数N无关,就可得到即SQL。需要注意的是,上述分析建立在N次测量中没有相互作用的基础上,通过制备纠缠、压缩态等手段,在每次测量之间增加耦合,可增加系统中的费雪信息,实现对测量不确定度σ的优化。

3 量子增强光学计量技术拓展的克拉美罗界

3.1 压缩态增强的干涉测量技术

利用干涉仪的相位测量是最常见的量子估计研究之一,其典型应用场景即长臂干涉仪对引力波的测量[14]。1981 年,Caves 提出了使用压缩状态减弱真空涨落噪声的方法[15]。

对经典的马赫-曾德干涉仪(Mach-Zehnder Interferometer,MZI)进行分析有助于量化量子涨落的影响。在分束器输入模态i0和i1的作用下,输出操作符b0和b1可表述为:

干涉臂b0上的强度为:

在经典环境下,在i0端口注入振幅为α光源,在i1端口注入真空模态,因此,可以用相应的经典数字替换操作符强度算符演化为:

此时,相位测量不确定度有[14-16]:

Canvas 的研究表明制约测量不确定度的散粒噪声源于真空涨落进入干涉仪导致的探测器波动,可以引入压缩态对这类波动进行抑制[12]。在传统的相干光中,正交振幅和正交位相的方差应该满足海森堡不确定性:Δ2xΔ2p≥1/4,但两者都不存在针对个体的测量下确界。因此,若想抑制振幅分量的方差(例如Δ2x=e-2s/2),就要方法位相分量的波动(例如Δ2p=e2s/2),进而引入压缩态。尤其需要注意的是,当振幅位相空间的方差分布以原点为中心时,该状态被称为压缩真空态(尽管压缩真空中的平均光子数不是零,而是ñ=sinh2(s))。当ñ≪|α|2时,在压缩场的作用下,相位测量的不确定度可以提高到σ2=e-2s/α2。费雪信息计算表明不确定度甚至可以进一步优化[17],得到:

如果此时能量在相干态和压缩态之间平均分配,即|α|2=ñ,测量不确定度逼近HL。实际压缩态在Fock 态中的表达如公式(11)所示,其的泵浦涉及到成对光子的产生:

式(11)中,ϑ与压缩正交相关联。

通过参量下转换或四波混频技术,可实现在实验中引入压缩态以达到四波混频产生的压缩光将噪声压制到真空噪声以下的目的[18],具体实验过程试验系统设计如图1 所示,实验结果如图2 所示。

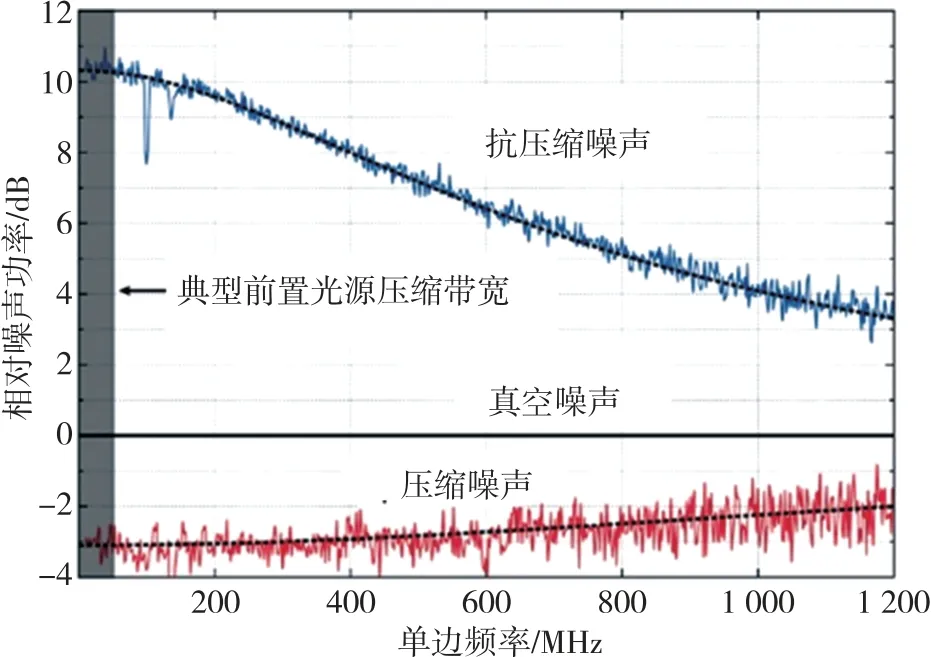
图2 光源宽带压缩特性测量结果图Fig.2 Measurement results of broadband compression characteristics of light sources

图1 中,系统设计的核心在于基于双凸周期性极化磷酸钛钾(PPKTP)晶体所产生的压缩真空态,尤其是端面采用反射镀膜,线宽2.26 GHz,并通过光学参数放大产生压缩。由图2 所示测量结果中压缩噪声曲线与抗压缩噪声曲线关系可得出结论如下:本技术极大延拓了压缩极限带宽。

压缩光磁场探测示意图及其对应的理论计算结果如图3 所示。耦合到微环面之前的压缩态及3种机械共振模式下的器件特性如图4 和图5 所示。

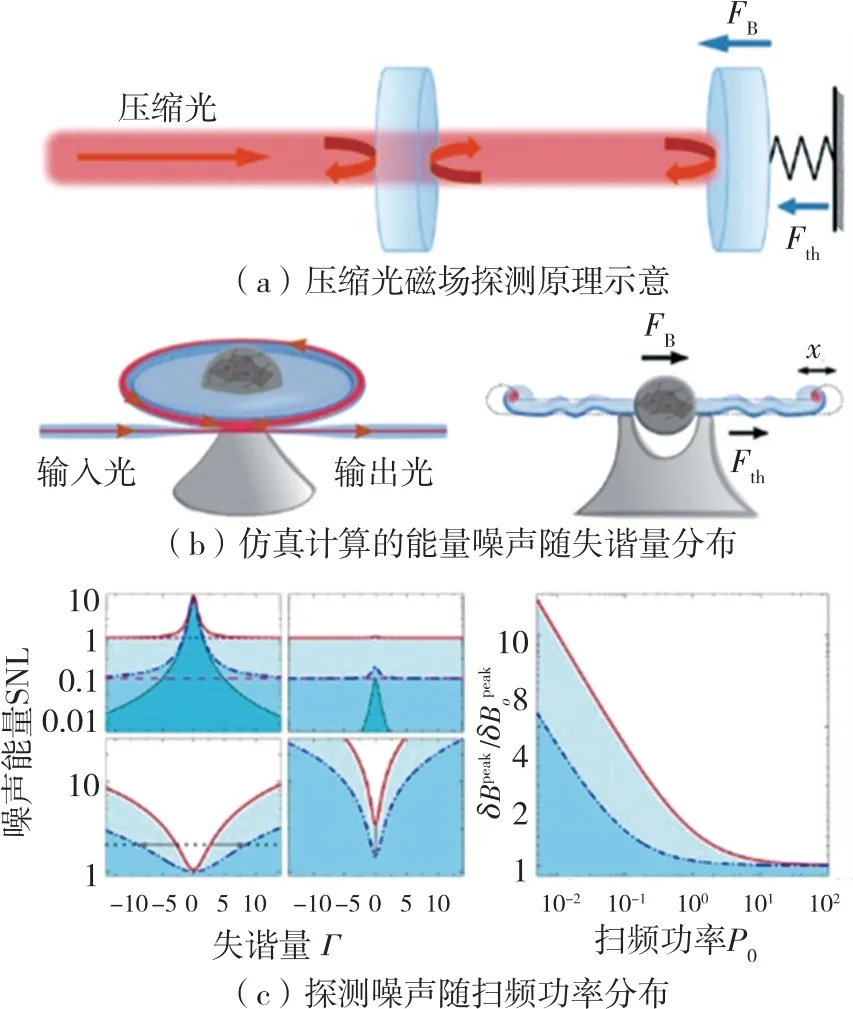
图3 压缩光磁场探测示意图及理论计算结果图Fig.3 Schematic diagram and theoretical calculation results of compressed optical magnetic field detection

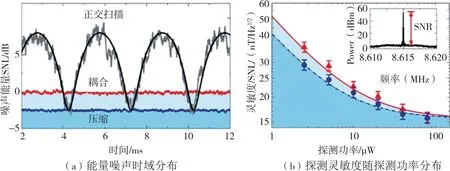
图4 耦合到微环面之前的压缩态扫描结果图Fig.4 Scanning results of scompressed state before coupling to the microtorus

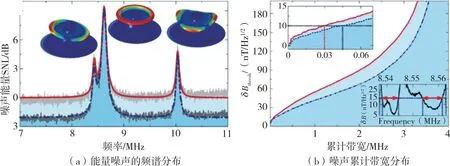
图5 3 种机械共振模式下的器件特性扫描结果图Fig.5 Scanning results of device characteristics under three mechanical resonance modes

图4(a)中,深灰色曲线表示本振连续扫描时的噪声功率;图4(b)中,红色和蓝色实心曲线为本振相位锁定在相位正交时相干和压缩探测器的噪声功率;图5(a)中的3 种机械共振模式下能量噪声与频率之间的关系分析如图5(b)所示,分析红蓝实线关系易得出压缩态探测相较于相干探测,无论是在灵敏度还是带宽上,都有着显著的提升。结合上述分析,可得结论如下:压缩光探测可极大提升弱磁场探测的灵敏度及带宽[19]。

在压缩态测量技术中,还需要考虑传输过程中光子的损耗η:如果传输中存在损耗,压缩正交态方差将是初始方差和真空方差的加权和:

方差的增加表明噪声抑制效果的减弱:真空态重新在测量结果中引入了散粒噪声。因此,引力波测试中多引入真空管道,降低传输过程中的光子损耗。

最近发展的量子精密测量技术还可能引入多个模式的耦合,以纠缠双模压缩真空态为例,两个压缩真空模式在对称分束器上的干涉纠缠,沿相空间的正交方向有相同的压缩水平。以位相p1和p2为例,它们在两种模态的正交值中显示相关性,由于差值的方差仍然低于真空噪声水平[20]。这意味着其共轭积分必须表现出增加的抖动。双模压缩真空态在量子密码学、量子通信等领域有重要应用[21-23],这些状态也可以通过非线性光学相互作用产生,在参数下转换或四波混频技术中,通过将泵浦模式耦合到较低频率的两个模式即可实现纠缠压缩,使其在笛卡尔坐标方向或平均波长上可区分。例如,将方差抑制一个因子e-2s就对应于状态为

与式(11)类似,ϑ表示一对压缩正交态。

由于这2 种模式的光子数完全相关,该技术可应用于量子成像和量子等离子体传感等领域。以如图6 所示的量子等离子体传感器为例,详细介绍了基于纠缠双模压缩真空态增强的等离子体传感及干涉技术。

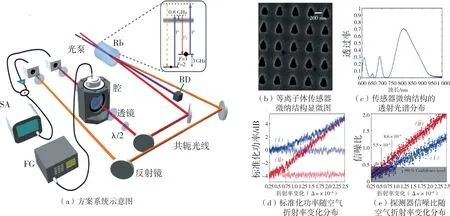
图6 双-Λ 能级四波混频方案图Fig.6 The scheme diagram of double Λ -level four-wave mixing

图6(a)中,基于四波混频过程产生的双光束中,探测光路FG 通过腔内的等离子体传感器,共轭光路SA 作为强度差噪声测量的参考[23]。图6(b)和6(c)分别为等离子体传感器的微纳结构及其透射光谱。观察图6(c)中曲线发现在795 nm 处,传感器的透射率约66 %。分析图6(d)和图6(e)所示曲线可知,当增加空气折射率的变化(Δn)时系统测量得到的信号,相较于相干光探测,双光束系统探测灵敏度最优可达4 dB 的优化。因此,该双Λ 装置四波混频方案可适用于检测空气折射率的微小变化,并且其灵敏度较之镜头噪声极限会更低[24,25]。

如图7 所示的双MZI 系统光路在每个输出端口中都有光隔离器,可以在测量读出信号的同时将独立压缩态(ISS)或孪生光束态(TWB)注入到反对称端口中。对于ISS 情况,计算输出的互相关,而对于TWB 情况,计算输出的差值。量子增强的测量信噪比曲线如图8 所示,以及为ISS 注入散粒噪声后的偏移量曲线间的超越特征。与单模MZI 测试类似,通过上述实验系统设计及结果分析,在证明了纠缠的有效性的同时也证明了式(13)中的理想双模压缩态是由损耗和寄生过程降级的实验情况的理想化,并进一步说明了公式对为后期实验设计的指导意义。

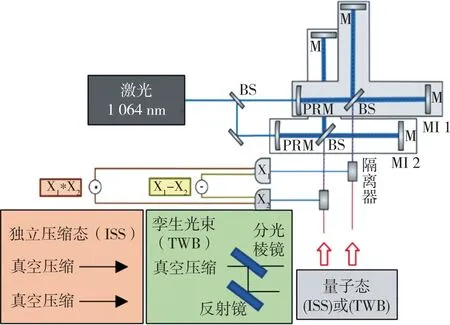
图7 双MZI 干涉测量光路示意图Fig.7 The schematic diagram of Double MZI interferometry measurement

3.2 固定的光子数态

量子光学相干衍射中的固定的光子数态是指具有固定光子数的量子态[26-30]。在这种态中,光子的数量是确定的,且光子的能量也是确定的[31,32]。该状态可以用Fock 态来描述,Fock 态是一种离散态,即在某个确定的时刻,态中只有某个确定的光子数。在Fock 态中,光子的位置、速度和相位都是不确定的,只有关于光子数的期望值是确定的。Fock 态在量子信息科学、量子计算和量子通信等领域有重要应用[33-35]。

在使用电磁场时,可指定固定运行中的可使用光子数量N的状态。对于相位估计,需要在传感臂和参考臂之间细分,当目标物体位于探测臂时,状态可表示如下:

图9 展示了在最佳测量方案中,解析两个输出光子数之前,将2 种模式叠加在分束器上即可根据不同占用数的观测频率重建相位

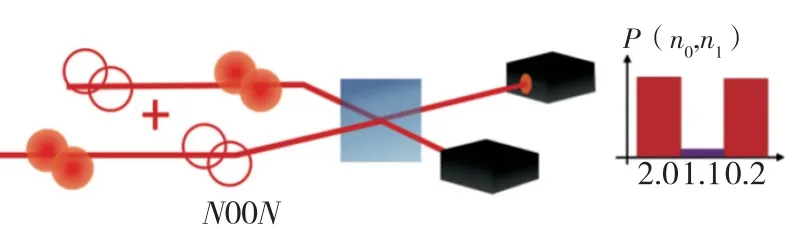
图9 当N=2 时的N00N 状态图Fig.9 N00N state diagram when N=2

双模纠缠N00N态是一种在量子光学中被广泛研究的态,它具备纠缠特性,可以用于量子干涉实验。具体地说,双模纠缠N00N态是由2 个光模所组成的纠缠态,其中每个模中都有N个光子。

式中:“|N,0〉”——模1 中有N个光子,模2 中没有光子;“|0,N〉”——模2 中有N个光子,模1 中没有光子。

如果将这个态输入到量子干涉仪中,就可以用来观察干涉效应。在干涉仪中,这个态会被分成两个部分,分别进入两个干涉臂。然后,这两个部分会发生相位差,并在干涉仪中形成干涉条纹。当这个态的光子数N很大时,干涉条纹的分辨率非常高,这是因为光子的波长很短。这使得双模纠缠N00N态在量子光学测量和计算中具有重要应用。例如,它可以用于高精度相位测量、光学量子计算、以及光学量子加密通信等领域。

4 结束语

量子光学增强计量是一个很有前途的领域,它可以利用光的量子特性来实现比经典方法更高的精度和灵敏度。然而,下一代仪器科学仍有许多挑战和开放性问题需要解决,例如如何生成、操作、检测、表征、控制、减缓和应用多模量子光源用于各种计量任务。通过这些领域的研究,可以期待在不久的将来,量子光学增强计量学将有更多的突破和应用。为推动量子光学计量技术,仪器领域应重点发展以下方向

1)生成和操作多模量子光源,例如光频率梳[26],可以在宽频谱上提供高维纠缠和压缩态。多模量子光源可以实现并行和多路复用量子计量协议,从而克服带宽限制,提高测量速度和分辨率;

2)多模量子光态的检测和表征可以提供不同模式和参数下QFI 和QCRB 的信息,也可以验证量子计量协议的性能。因此需要发展多模量子光态的检测和表征技术,如零差探测技术[26],光子数分辨探测技术[27],或量子态层析技术等[27];

3)控制和减轻多模量子光态的噪声和退相干效应,如使用反馈环[23]、纠错码[24]或自适应测量[27]。噪声和退相干效应会降低多模量子光态的量子相关性和相干性,从而降低其计量优势。控制和减缓噪声和退相干效应可以保持或恢复多模量子光态的量子特性。

此外,需开发多模量子光源与原子、分子、纳米光子器件等物理系统的应用与集成技术,进一步为传感、成像、光谱学、通信、计算等应用领域的开发和应用提供必要的支持和保障。