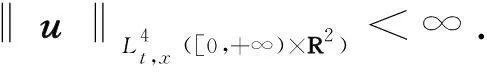二维三次非线性薛定谔方程组的极小质量爆破解
2023-07-13吴清迪
吴清迪
(河海大学 理学院,江苏 南京 210098)
0 引 言

考虑如下的二维三次非线性薛定谔方程组:
(1)
等价地,可以将(1)写为向量形式
i∂tu+Δu=F(u),
(2)

相比于薛定谔方程,方程组中2个分量的相互作用和影响使得方程组的求解和证明更加困难,因此在证明过程中考虑分量的估计和带来的不同结果显得至关重要.为解决该问题,笔者利用向量表示方法简便解的表达.因此,在下文中将会根据叙述过程中的不同情况分别使用方程组形式或向量形式来表示.
定理1当临界质量m0有限时,存在一组质量为m0的极大存在时间解u=(u1,u2),并且解u向前和向后都爆破.同样地,质量为m0的向前和向后都爆破的极大存在时间解,在模去变换群G后是几乎周期的.
1 预备知识
为了得到本文的主要结果,给出如下定义和定理.
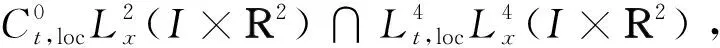



此外:



(3)
根据定理2之ii)可得,对于m≤C-1有
A(m)≤Cm2.
(4)
另一方面,根据方程组的解关于初值的连续依赖性,得到A是左连续的.所以,一定存在唯一的临界质量0

将定理1归结为研究一类特解,即这些解是相位旋转、调制、空间平移和伸缩等对称性的几乎周期解,所以接下来介绍对称性的相关性质.
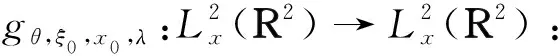
令G为满足上式变换的集合,则G是由相位旋转、频率调制、平移和伸缩产生的群.




(5)
2 主要结论的证明
在证明定理1之前,首先给出命题1及其证明,然后利用命题1证明本文的主要结论.

(6)

为证明命题1,在接下来的2小节中分别回顾稳定性引理和线性轮廓分解.
2.1 稳定性引理

(7)
其中,常数0 引理1[6]对每个A>0和ε>0,存在δ>0满足以下性质: (8) (9) (10) 此外,对任意的l≥1,有质量分离: (11) 根据un的时间平移不变性,可以选取tn=0,从而有 (12) (13) (14) 假设存在ε>0满足 (15) 下面将证明(15)与(12)矛盾. 因为A是单调递增,并且在区间[0,m0-ε]上是有限的,所以结合上述性质,可以得到边界条件:对所有的0≤m≤m0-ε以及常数0 A(m)≤Bm. (16) 因为A(m-ε)是有限的,所以由(15),(16)和定理2得 M(v(j))=M(φ(j))≤m0-ε, 和 (17) 根据(5),(12)和三角不等式,以及(14)和(17)有 (18) 然后,通过公式 (19) 对上式进行化简得 根据(13)和(19)即证 (20) 令 (21) 令δ>0并且其取值和Bm0有关,当l和n充分大时,由(18)可以得到 由(20)和(21)可得 将上式与(13)比较,可知至多有一个φ(j)非0,所以轮廓分解简化为 un(0)=hneitnΔφ+wn. (22) 但这与(12)矛盾.同样地,tn趋于-∞时情况类似. 综上所述,当tn收敛到0时命题1成立.

2.2 线性轮廓分解
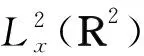

2.3 命题1的证明



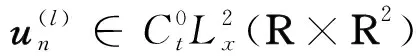
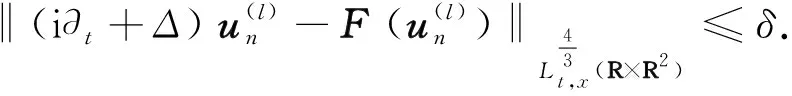
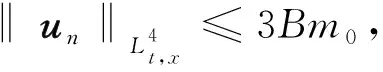





2.4 定理1的证明