基于模糊滑模直接横摆力矩的车辆横摆稳定性控制

胡建军，肖 凤，林志强，黄 健，邓承浩，3

（1.重庆大学 机械与运载工程学院，重庆 400044；2.重庆大学 机械传动国家重点实验室，重庆 400044；3.长安新能源汽车科技有限公司 重庆 400023）

车辆主动安全系统提高了车辆对各种行驶状态和道路环境的适应性，为了满足车辆在转弯等一些复杂工况下的主动安全性能，汽车电子稳定性系统（electronic stability program，ESP）得到普及［1］。在ESP 控制方面，四轮独立驱动电动汽车凭借其四轮力矩独立可控、电机响应速度块、控制精度高等巨大优势［2-3］而被广泛应用于ESP研究。

目前ESP 大致可分为两种，一种是直接横摆力矩控制（direct yaw-moment control，DYC），另一种是主动前/后轮转向系统（AFS/ARS）。DYC 是基于差动制动/驱动的思想，利用两侧车轮不同的制动/驱动力形成的横摆力矩补偿车辆需求横摆力矩，使车辆的行驶轨迹跟随驾驶员意图；AFS/ARS 能够给前/后轮一个附加转角，从而在不改变车轮纵向力的条件下实现对横摆力矩的控制。Wang 等［4］设计了差动驱动辅助转向（DDAS）和直接横摆稳定性协同控制策略，在多种典型工况下都能提高车辆的操纵稳定性。文献［5］采用前轮差动制动和后轮主动转矩矢量集成控制对装备了主动差速器的后驱车辆进行横摆稳定性控制。文献［6］基于耗散性理论对DYC和AFS集成控制来提高车辆操纵稳定性。

分层结构的横摆稳定性控制策略是当前的一种主流控制结构，并得到了广泛的应用［7］。在上层结构的需求横摆力矩计算中，比例‒积分‒微分控制（PID）、线 性 二 次 型 调 节 器 （linear quadratic regulator，LQR）、滑模控制 （sliding mode control，SMC）以及模型预测控制（model predictive control，MPC）的使用较为普遍，PID 控制过于依赖经验，LQR 和MPC 对车辆状态模型的精度要求较高，且MPC计算量大，难以在实车上使用，SMC 因其变结构的特性，对外界干扰的强鲁棒性等优势［8］在车辆横摆稳定性控制中得到了最广泛的使用。文献［9］利用 SMC 以横摆角速度和质心侧偏角为控制变量构建滑模面，并利用控制律得到需求横摆力矩，从而实现车辆稳定性控制。文献［10］提出的自适应滑模DYC 控制方法利用不同的控制增益来适应前后轮胎侧偏角的变化，增强了车辆对参数变化和不确定性的鲁棒性。在文献［11］中比例积分 SMC 被提出，旨在借助积分项减少误差。然而，在传统SMC中存在非常关键的一个问题，SMC会造成控制系统的抖振，它可能导致机械部件疲劳，并在短时间内摧毁系统［12］。

在下层结构的车轮力矩分配中，文献［13］以最小化轮胎滑动能量损失为目标进行转矩分配，并与轮胎附着利用率最小的分配策略进行对比，验证了前者在效率方面的提高。文献［14］以轮胎利用附着利用率最小的方法对车轮转矩进行分配，使其稳定裕度最大从而提高车辆应对危险工况的稳定性。文献［15］建立了分段线性轮胎侧偏力的混合逻辑动态（MLD）模型，并将其应用于控制器中求解额外的直接横摆力矩，根据拟合的轮毂电机效率曲线，分配4个轮毂电机力矩，同时实现电机效率最优和目标横摆力矩的跟随。然而上述方法大多都是直接对车轮力矩进行控制，很少考虑轮胎滑动率对车辆横摆稳定性的影响。这将会使车轮容易出现过度滑转或抱死的危险情况，从而造成车辆稳定性急剧降低。

为了解决在车辆横摆稳定性控制中出现的系统抖振现象以及轮胎滑动率超出合理范围的问题，本文以四轮独立驱动电动汽车为研究对象，提出了一种具有上层控制器和下层控制器两层结构的模糊滑模直接横摆力矩控制策略，提高了车辆的横向稳定性，并能抑制传统滑模控制器造成的系统抖振。

1 系统建模

本文建立了包含车身的横向、纵向、横摆、侧倾4个自由度以及4 个车轮旋转的8 自由度车身动力学模型（图1），其主要参数如表1所示。

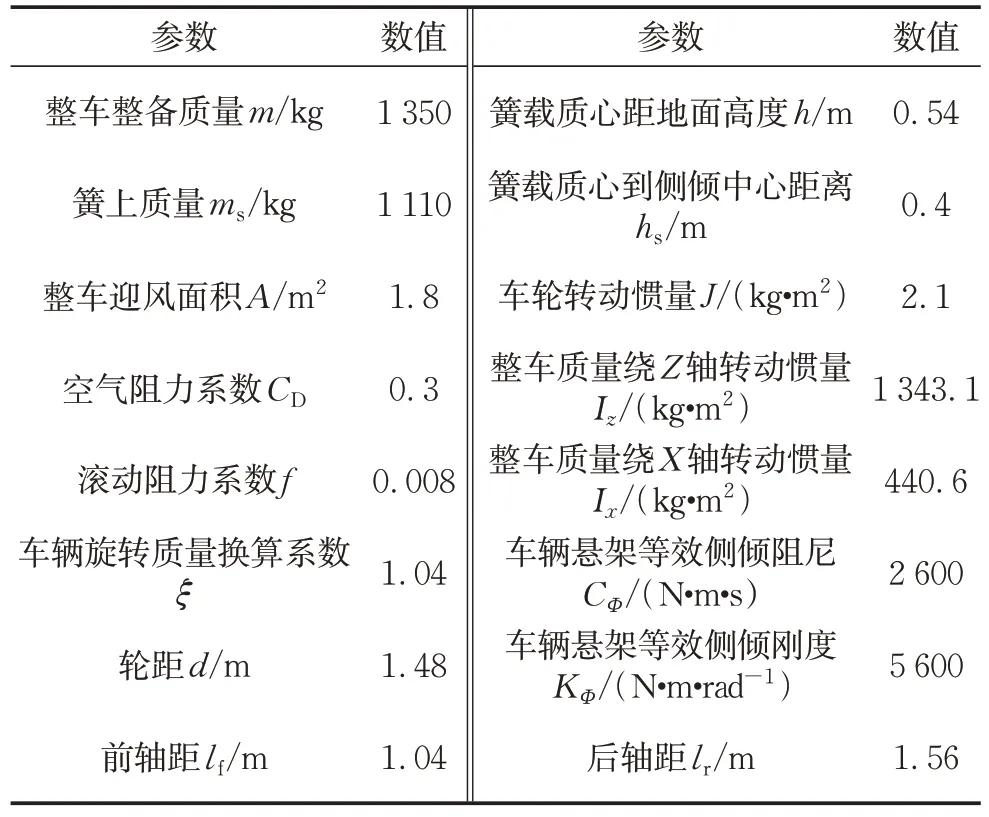
表1 车辆结构参数Tab.1 Vehicle structure parameters

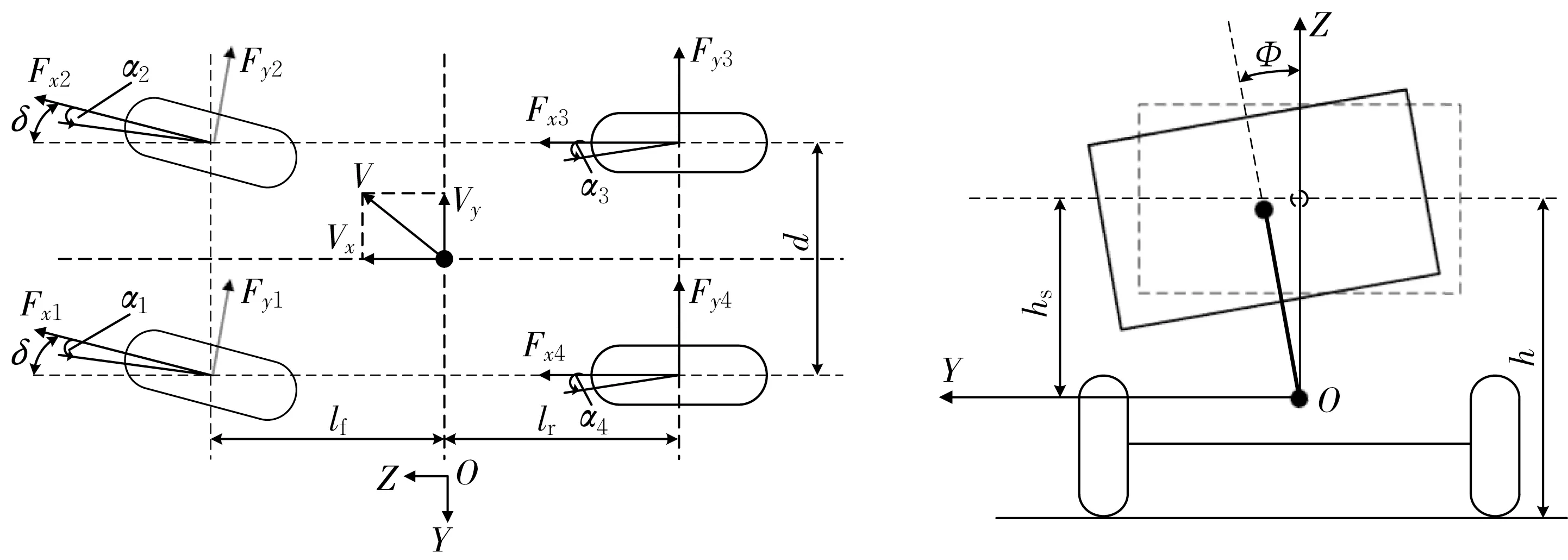
图1 车身动力学模型Fig.1 Body dynamics model

车身动力学模型4个自由度的动力学表达式分别为

式中：Vx和Vy分别为汽车质心处的纵向和横向车速；r为横摆角速度；Fxi、Fyi分别为地面对车轮作用的纵向力和侧向力，其中i=1，2，3，4分别表示左前，右前，右后，左后车轮；δ为前轮转角；Φ为车身侧倾角；g为重力加速度；式中其余变量含义如表1 中所示。

采用魔术公式对轮胎进行建模，其表达式为

式中：Y(X)为轮胎所受的纵向力、侧向力或回正力矩；X为轮胎滑动率或侧偏角；SH和SV分别为轮胎曲线水平偏移量和垂直偏移量，主要表征车轮外倾角和轮胎制造误差对轮胎力学特性的影响；B、C、D、E分别为刚度因子、形状因子、峰值因子和曲率因子。

在车辆的行驶过程中，车轮的旋转运动和滑动率可分别由式（8）和（9）表示。

式中：Iw为车轮的转动惯量；Rw为车轮转动半径；ωi、λi、Tdi、Tbi、Vwxi分别为第i个车轮对应的转速、滑动率、驱动力矩、制动力矩和车轮中心速度，由于本文只对车辆的制动工况进行研究，故Tdi=0。其中车轮中心速度Vwxi可由式（10）计算得到。

轮胎侧偏角可由式（11）、（12）计算得到。

式中：αf和αr分别为前轮和后轮的侧偏角；β为车辆质心侧偏角。

地面对每个轮胎的垂向载荷计算方法由式（13）给出。

式中：Fzi为地面对第i个车轮的垂向载荷；h为簧载质量中心到地面的高度；KΦf和KΦr分别为前后侧倾刚度；CΦf和CΦr分别为前后阻尼；hf和hr分别为前后轴侧倾中心高度。

式中：Tm为电机实际输出力矩；T*m为电机期望输出力矩；τm为时间常数；km为系统延迟。

采用一阶惯性延迟系统代表机械制动系统响应过程进行建模，即

式中：Tf为实际机械制动力矩；T*f为期望机械制动力矩；τf为机械制动系统时间常数；kf为机械制动系统延迟。

2 模糊滑模DYC控制器设计

为使车辆在不同附着路面下都能保证车辆稳定控制，并有效抑制采用滑模控制引起的抖振以及解决轮胎滑动率超出合理范围的问题，本文提出了一种分层结构的模糊滑模直接横摆力矩控制框架，如图2 所示。根据驾驶员输出的前轮转角δ和期望的纵向车速Vxd，基于二自由度车辆动力学模型，得到理想横摆角速度rd和质心侧偏角βd。在上层控制器中，将方向盘转角的绝对值和路面附着系数作为模糊控制器的输入量，动态调节滑模控制器的趋近率参数kd和ε，使滑模DYC 控制器能实时适应车辆行驶工况，对4 个车轮纵向力Fxi_tar进行分配。下层控制器通过对车轮力矩Ti_tar进行控制，从而将上层控制器计算得到的车轮纵向力得以实现。

图2 模糊滑模DYC控制框架Fig.2 Framework of fuzzy sliding mode DYC controller

从车辆动力学角度看，横摆角速度和质心侧偏角与车辆的操纵稳定性密切相关。以二自由度模型为参考模型（图3），基于本文所提控制框架，使得车辆状态可以跟随理想的横摆角速度和质心侧偏角。

图3 二自由度车辆模型Fig.3 Vehicle model of two-degree-of-freedom

动力学方程可以表示为

式中：Kf和Kr分别为前后轴轮胎等效侧偏刚度；β为车辆质心侧偏角。在本文中，车辆横摆角速度和质心侧偏角理想值如下［16-17］：

近日，2018年第二批广西创新小镇培育名单公布。据了解，创新小镇是指相对独立于城市中心区，具有明确产业定位、科技创新、文化内涵、生态特色、旅游特征和一定社区功能的创新发展空间平台。

2.1 上层控制器

滑模控制切换函数的选择对控制效果的影响至关重要，为了同时对车辆横摆角速度和质心侧偏角进行控制，本文采用如下切换函数：

式中：s为切换函数；w为权重系数。

对式（19）求导，得

车辆总横摆力矩为

采用指数趋近率，有

式中：ε和kd为趋近率参数，ε>0，kd>0。

将式（20）、（22）代入式（21），得到总需求横摆力矩为

为了削弱滑模控制器的抖振，将饱和函数sat(s)代替符号函数sgn(s)，饱和函数sat(s)表达式由式（24）给出，其中Δ为边界层厚度。

根据式（23）可以看出，车辆总的需求横摆力矩直接受到滑模控制器趋近率参数的影响，本文基于模糊控制对滑模控制器的趋近率参数ε和kd进行优化，以削弱控制系统的抖振。本文所提模糊控制器中输入输出的论域都分为5个模糊语言变量：SS、S、M、B、BB，分别表示很小、小、中、大、很大。趋近率参数kd和ε的模糊规则如表2所示，并得到模糊控制输入输出隶属度曲面如图4所示。

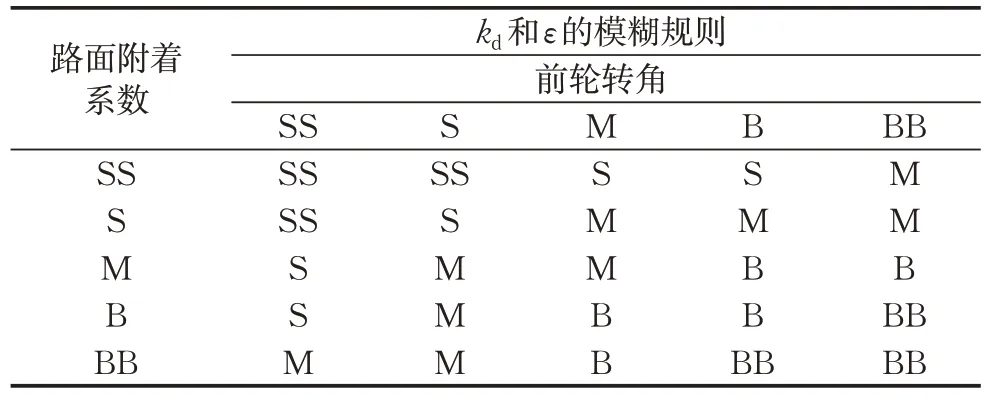
表2 趋近率参数kd和ε的模糊规则Tab.2 Fuzzy rules for approaching rate parameters kd and ε

图4 输入输出隶属度曲面Fig.4 Membership surfaces of input and output variables

假设转向轮转角很小，忽略转向轮纵向力在车辆Y方向的分量，通过改变前后轮纵向力比例来研究不同车轮纵向力分配对车辆横摆稳定性的影响。令

式中：Fxl为左侧前后车轮纵向力总和；Fxr为右侧前后车轮纵向力总和；a为前车轮纵向力在左侧车轮总纵向力中的占比，a=0，0.25，0.50，0.75，1.00；b为右前车轮纵向力在右侧车轮总纵向力中的占比，b=0，0.25，0.50，0.75，1.00。这样就得到了25 种轮胎纵向力分配方法。另外，为了充分利用轮胎与路面的附着条件，得到式（29）所示按地面对轮胎的垂向载荷比例对前后轴轮胎的纵向力分配的方法。

为了研究不同车轮纵向力分配对车辆横摆稳定性的影响，对以上26种分配方法分别进行仿真。车辆初始车速设置为80 km∙h-1，路面附着系数为1，前轮转角幅值为0.09 rad，周期为2.5 s（图5）。仿真结果如图6、图7所示，并得到载荷分配系数为0.006 4时的横摆角速度跟随误差绝对值均值，如表3所示。

表3 载荷分配系数为0.006 4时的横摆角速度跟随误差绝对值均值Tab.3 Mean absolute value of yaw rate following error at load distribution coefficient of 0.006 4

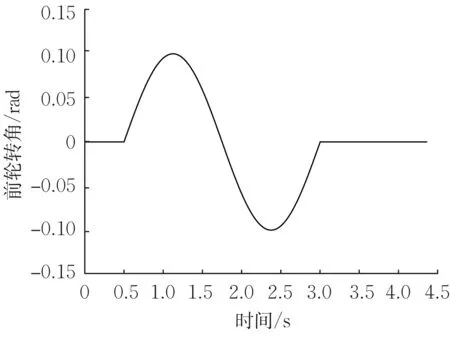
图5 前轮转角Fig.5 Steering wheel angle

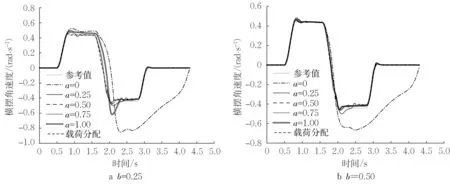
图6 横摆角速度Fig.6 Yaw rate

图7 行驶轨迹Fig.7 Driving trajectory

从表3 可以看出，当a=0 或b=0 时，代表一侧车轮中的一个未施加控制，处于滑行状态，此时车辆发生失稳，横摆角速度和行驶轨迹严重偏离期望值，这是因为未施加控制的车轮与地面间的附着力没有得到利用，其它3 个车轮提供的纵向力和侧向力不足导致了车辆的横向失稳。由图6和图7可以看出，前后车轮纵向力分配越均匀，车辆横摆角速度和行驶轨迹呈现越接近期望值的趋势。表3为车辆横摆角速度跟随误差绝对值均值，它代表对期望横摆角速度的跟随效果。从表3中可以发现，当a和b越接近载荷分配系数时，横摆角速度跟随误差绝对值均值越小，即横摆角速度的跟随效果越好。由于充分利用了轮胎与路面的附着条件，按轮胎垂向载荷分配的横摆角速度跟随误差绝对值均值为0.006 4，小于均匀载荷分配的误差绝对值均值0.006 9，具有更好的控制效果。因此在DYC控制器的设计中，为了充分利用轮胎与路面间的附着力，取得更好的控制效果，应尽量将轮胎力按照地面对不同轮胎垂向载荷的大小进行分配。

2.2 下层控制器

下层控制器主要通过控制每个车轮的驱动/制动力矩来实现上层控制器获得的车轮目标纵向力。现有的研究大多都采用如式（30）所示的简化算法对车轮力矩进行直接控制。

式中：Ti_tar为第i个车轮的目标控制转矩，当Ti_tar>0，车轮处于驱动状态，当Ti_tar<0，车轮处于制动状态。本文引入轮胎滑动率作为中间控制变量，通过控制车轮转矩来控制目标滑动率的跟随，最终实现车轮目标纵向力。

由魔术轮胎公式可知，轮胎的纵向力Fxi是关于垂向载荷Fzi、轮胎侧偏角αi、滑动率λi和路面附着系数μ的四元函数，记为

当滑动率超过A点时，轮胎纵向力开始下降，同时侧向力系数也急剧下降，为了保证轮胎有足够的侧向力余量，取B点作为滑动率的上限，λB=0.95λopt，并得到轮胎纵向力的约束条件为

如图8 所示，每个车轮目标纵向力Fxi_tar对应着两个滑动率λL和λH。H点处轮胎力处于非线性区，侧向力性能要远低于L点，因此采用滑动率较低的L点λi_tar作为目标纵向力Fxi_tar对应的目标滑动率。

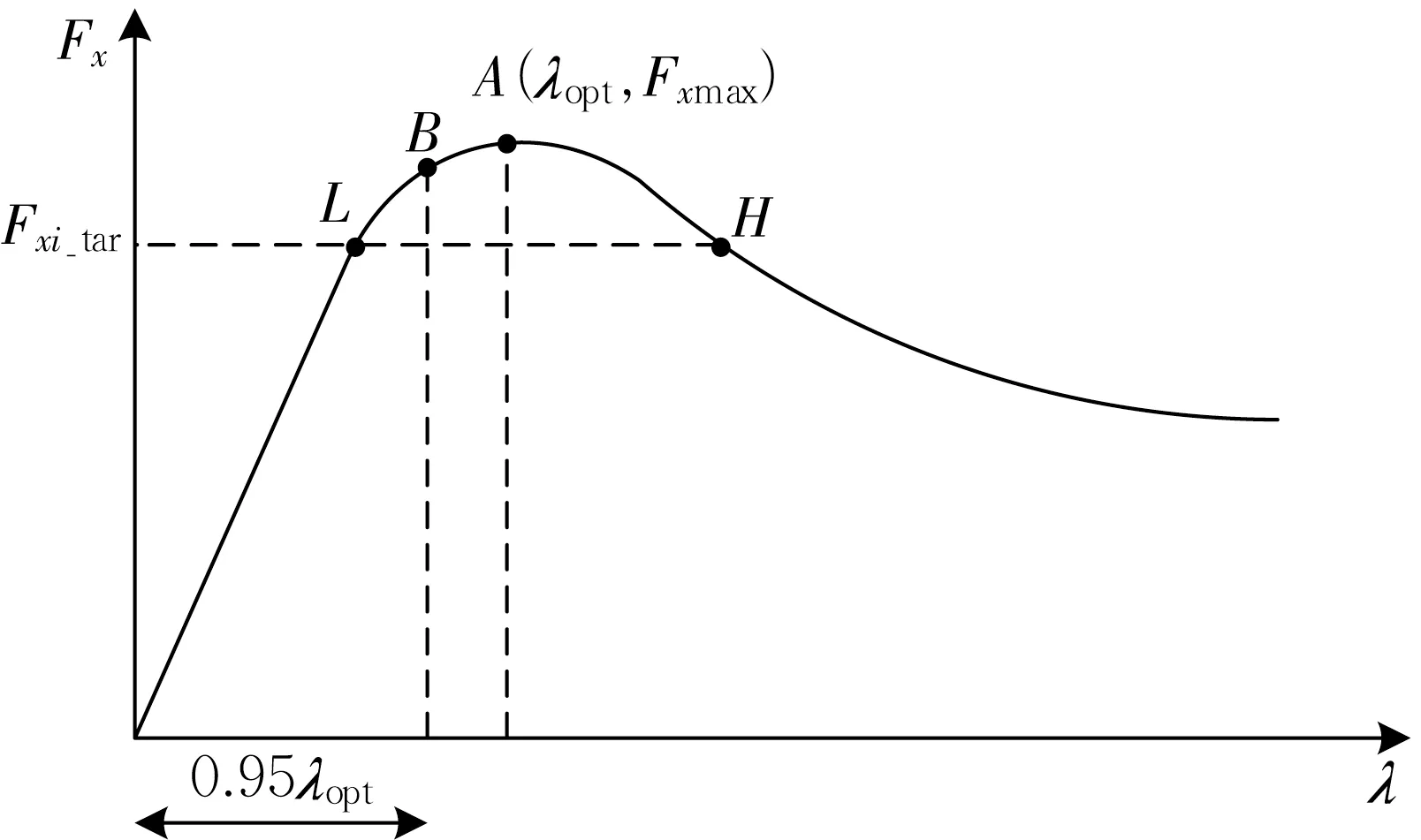
图8 轮胎纵向力和滑动率关系曲线Fig.8 Tire longitudinal force versus slip rate

本文使用滑模控制来实现目标滑动率的跟随，滑模面定义为

采用指数趋近律，有

式中：ε和kd为趋近率参数，ε>0，kd>0。

结合式（8）、（9）、（35）、（36），得到车轮力矩的控制律为

考虑车轮最大制动力矩和电机最大输出转矩的限制，车轮目标控制力矩还需满足以下约束：

式中：Tm_max为电机最大输出转矩；Tb_max为制动系统可提供的最大制动力矩。

3 仿真实验及结果分析

为了验证本文设计的模糊滑模DYC 控制器的控制效果，本文分别在高附着和低附着路面下对其进行单移线工况仿真试验（图5）。

3.1 高附着系数路面

本文采用单移线工况来验证车辆在高附着系数路面模糊滑模DYC 控制器的性能。初始车速和路面附着系数分别设定为100 km∙h-1和1，模糊滑模DYC、滑模DYC、无控制仿真结果如图9所示。

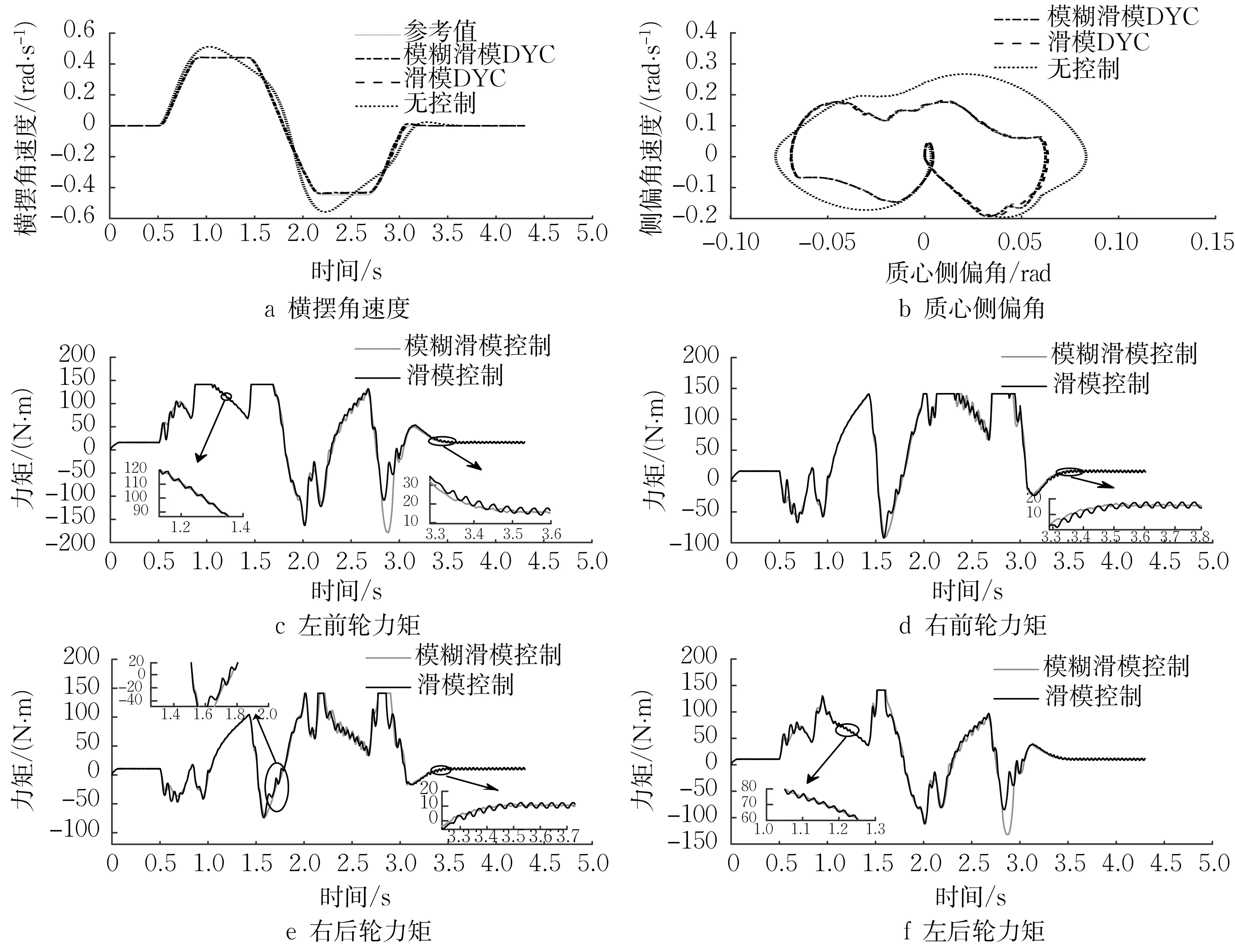
图9 高附着系数路面仿真结果Fig.9 Simulation results of high adhesion coefficient pavement

从图9a 可以看出，未施加控制车辆的横摆角速度与参考值存在着较大的偏差，而在模糊滑模DYC和滑模DYC的控制下，车辆的横摆角速度基本与参考值重合，说明车辆能跟随驾驶员的行驶意图。由图9b 可以看出，相比于无控制车辆，模糊滑模DYC和滑模DYC控制下的车辆质心侧偏角更向0 收敛，这说明车辆的横摆稳定性得到了提高。此外，由图9c～9f 的车轮力矩仿真结果可以发现，在模糊滑模DYC控制器的作用下，车轮力矩的抖振得到比较明显的削弱。

3.2 低附着系数路面

为了进一步验证车辆在低附着系数路面模糊滑模DYC控制器的性能，初始车速和路面附着系数分别设定为50 km∙h-1和0.3，仿真结果如图10所示。

图10a中，无控制车辆的横摆角速度已经完全偏离了期望值，车辆发生了严重的横向失稳，而模糊滑模DYC和滑模DYC控制使车辆的横摆角速度依旧跟随参考值，车辆的横向稳定性得到了保证。另外，从图10a 中还可看出，滑模DYC 作用下的车辆横摆角速度发生明显的抖振，极大地降低了乘员的乘坐舒适性，而在模糊滑模DYC控制器作用下的车辆横摆角速度基本趋于平稳。图10c～10f的车轮力矩仿真结果显示，滑模DYC作用下的车轮力矩发生了剧烈的振荡，而模糊滑模DYC有效的抑制了系统的抖振，控制车轮输出平稳的力矩。综上所述，本文提出的模糊滑模DYC 控制策略能有效地满足车辆的横向稳定性并使传统滑模控制器的抖振现象得到削弱。

4 结论

为了避免车辆发生横向失稳的风险，本文根据四轮独立驱动电动汽车四轮力矩独立可控的特点，引入轮胎滑动率作为中间变量对车轮力矩进行控制，并将控制系统抖振的问题考虑在内，提出了一种具有上层控制器和下层控制器两层结构的模糊滑模直接横摆力矩控制策略。仿真结果表明，该模糊滑模直接横摆力矩控制策略在不同的附着路面条件下都能保证车辆的横向稳定性，并能削弱传统滑模控制器带来的系统抖振现象。

作者贡献声明：

胡建军：提出研究思路，设计研究方案，对论文提出修改意见，为论文研究工作提供项目支撑。

肖 凤：修改完善论文，分析模型车实验数据，给出初步结论，回复审稿意见，负责最终版本修订。

林志强：参与研究，分析数据，对论文提出修改意见。

黄 健：撰写论文初稿。

邓承浩：技术支持，整理文献。