钻地爆炸耦合地冲击等效计算理论与方法

徐天涵，邱艳宇，谢 方，王明洋，3

（1.陆军工程大学 爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007；2.武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070；3.南京理工大学 机械工程学院，江苏 南京 210094）

目前，军事强国已投入实战的制导钻地炸弹侵彻更深，破坏作用更大，对浅层防护工程构成现实威胁；已列装的钻地核弹爆炸产生的耦合地冲击作用对深层防护工程威胁巨大。钻地爆炸对地下工程产生的破坏效应与其地冲击特征密切相关。因此，准确评估地冲击是地下防护工程设计计算的基础。

与空爆和触地爆相比，地下爆炸的耦合地冲击强度大大增强，且随着埋深增大，地冲击强度增大。达到封闭爆埋深时，地冲击强度达到最大值，不再随埋深增大而增大。由于封闭爆可简化为无限介质中的球对称爆炸，因此可方便地利用爆炸力学理论进行计算［1-2］。对于触地爆和非封闭的地下爆炸，由于地表自由面的影响，理论求解较为困难，一般利用试验手段测量地冲击大小，或进行数值模拟计算。为表征地冲击的耦合程度，引入耦合系数，其定义为地下爆炸地冲击与封闭爆或触地爆地冲击的比值。若以封闭爆为基准，则耦合系数小于1，仅当封闭爆时耦合系数等于1，表征了地表自由面对地冲击的削减作用；若以触地爆为基准，则在地表时耦合系数等于1，随埋深增大耦合系数增大，表征了埋深增大对地冲击的放大作用。

以不同的地冲击参数为研究对象，可得到不同的耦合系数。目前较为常用的为美国学者根据数值模拟给出的和俄罗斯学者根据试验给出的地冲击能量耦合系数曲线［3-4］。地冲击能量指介质运动的机械能。此外，国内外研究人员利用不同埋深的化爆试验给出了不同介质中地冲击应力、等效当量等参数的耦合系数变化曲线［5-14］。利用耦合系数可以直观表征地下爆炸的耦合效率，同时也可方便计算任意深度的地冲击大小。

相关研究已取得了较为丰富的成果，但对于耦合系数的计算仍主要依靠试验和数值模拟，对于地冲击的耦合机理和理论表征仍需进一步研究。不同耦合系数之间的转换关系尚未给出，导致不同的研究成果之间难以形成统一、普适的结果。本文在现有研究基础上，针对上述问题，分析地冲击与爆炸破坏区尺寸的关系，据此建立不同耦合系数之间的转换关系，给出耦合系数计算方法。

1 地下爆炸破坏区特征与常用耦合系数

钻地爆炸瞬间，与装药直接接触的介质受到强烈压缩，介质结构完全破坏，在挤压作用下形成一个空腔，该范围称为压缩范围，对应半径为压缩半径ra。介质中爆炸压力随爆心距增加迅速减小，当压力小于岩体介质的压缩强度时，介质不会压坏。但介质仍在进行径向运动，因此在环向会受到拉应力作用，若拉应力大于岩体抗拉强度，则会产生径向裂缝，由于岩体、混凝土等介质的抗拉强度比抗压强度小得多，因此压缩范围外就出现了比压缩范围大得多，以产生裂缝为主的破坏区，其半径为破坏半径rp。破坏范围外只产生很小的弹性变形，称为弹性区。当空腔内爆炸产物卸荷后，受压缩的空腔会向爆心方向发生部分回弹，从而在介质中产生环形裂缝。

对于接触爆炸，如图1a所示，其装药中心位于地表，压缩范围与破坏范围的截面形状近似抛物线型［15］，此时爆心下方的压缩半径与破坏半径分别为ra0与rp0，地表水平面的压缩（成坑）半径与破坏半径分别为ra*与rp*。接触爆炸的压缩半径与破坏半径比封闭爆炸的要小，这是由于部分能量泄入空气中，减小了装药对介质的破坏作用。

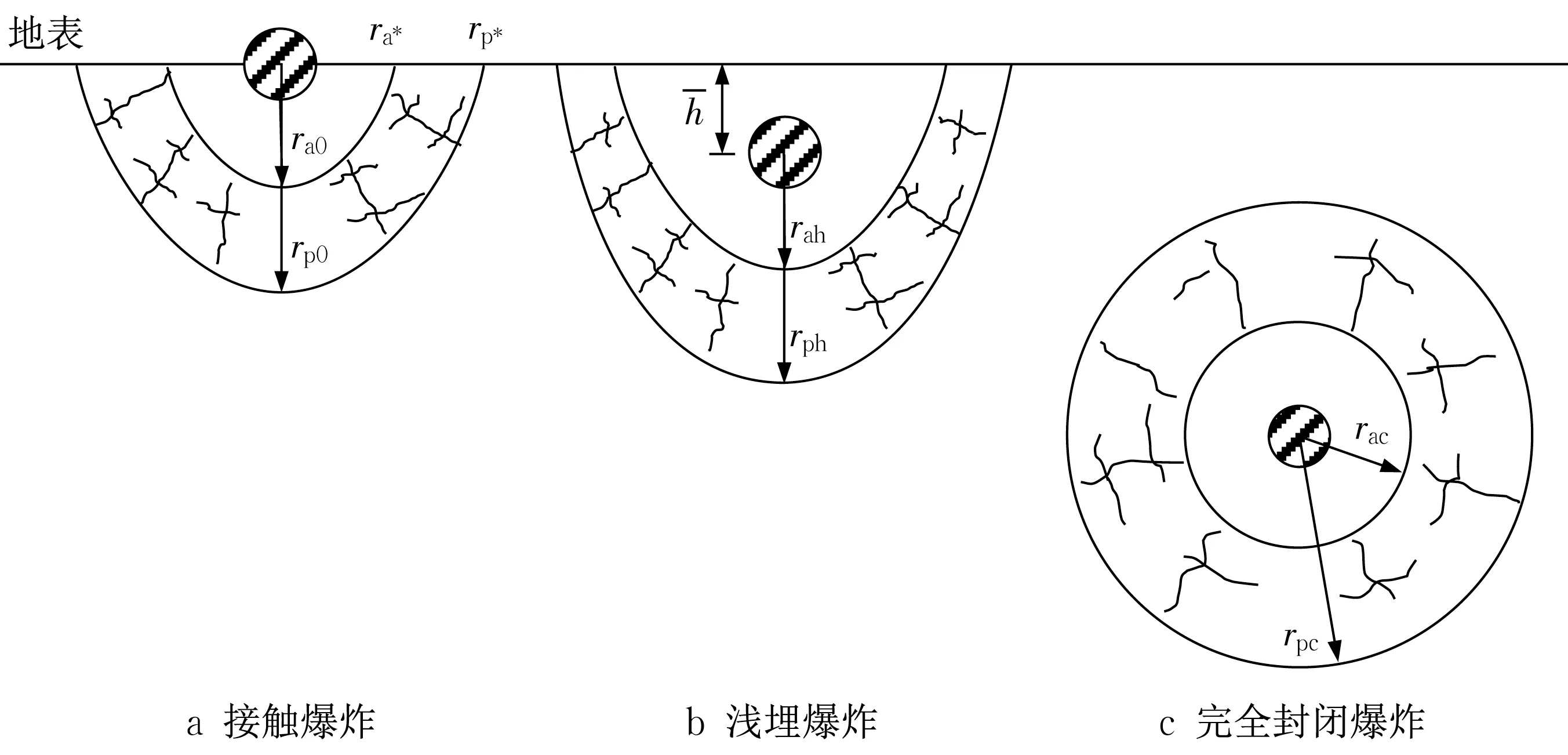
图1 地下爆炸示意图Fig.1 Diagram of underground explosions

对于地下爆炸，如图1b所示，比例埋深（爆深与当量的立方根之比）为hˉ时爆心下方压缩半径与破坏半径分别为rah与rph。随着埋深增加，压缩半径与破坏半径逐渐增加，直至某一深度后与封闭爆炸的值相等，继续增加埋深也不再变化。

对于完全封闭爆炸，如图1c所示，地表自由面的影响可忽略，爆炸后周围介质同时受到爆炸产物的作用，爆炸产生的压缩区与破坏区均近似为球形，半径分别为rac与rpc。相关研究［1，2，16］已形成了较为准确的计算公式。

浅埋爆炸地冲击是十分复杂的耦合作用问题，理论研究和试验均存在困难。通常是通过耦合系数将其转化为等效的封闭爆炸或接触爆炸进行计算。国内外常用的地冲击耦合系数有如下几种：

（1）地冲击能量耦合系数ηe，定义为相同介质、相同爆炸当量情况下，地下爆炸地冲击能量与封闭爆炸地冲击能量之比［3］，即

式中：Wsc为封闭爆炸地冲击能量；Wsh为比例埋深hˉ处的爆炸地冲击能量。

地下爆炸地冲击能量向四周传递，但对地下防护工程安全设计而言，有效的地冲击能量通常是位于爆心下方半空间的部分。因此，对应的耦合系数即可分为全部能量耦合系数ηet和有效能量耦合系数ηef。通过数值模拟和现场试验，美国学者与俄罗斯学者分别给出了地下核爆的有效能量耦合系数曲线［3-4］，如图2所示。

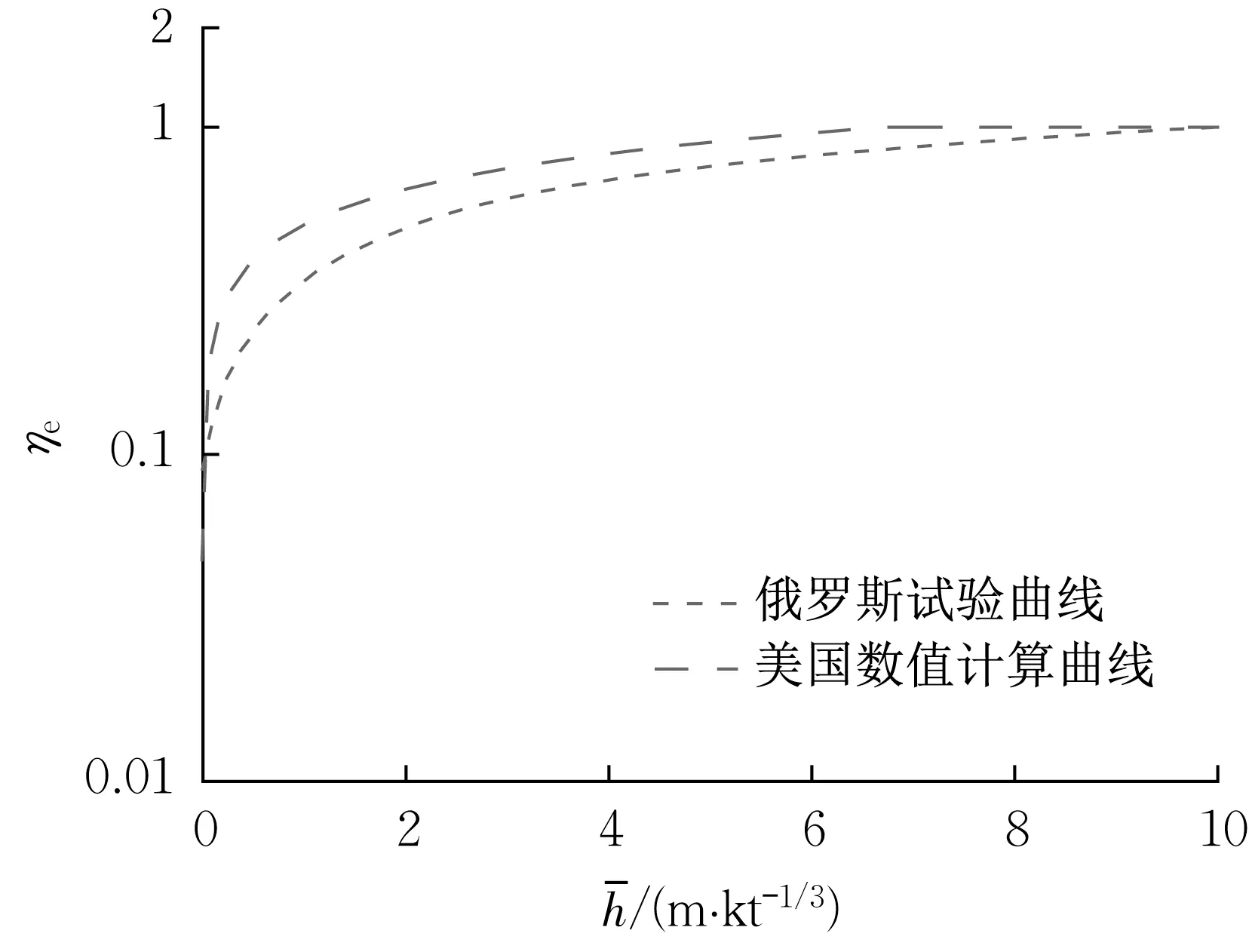
图2 美国与俄罗斯有效能量耦合系数曲线Fig.2 Curves of effective energy coupling factor of the United States and Russia

（2）当量耦合系数ηQ，定义为相同介质、相同爆距处，产生相同地冲击参数大小的封闭爆炸与地下爆炸的当量之比［12］，即

式中：Q为比例埋深为hˉ的爆炸当量；Qeff为等效的封闭爆炸当量。

利用当量耦合系数可以方便地换算地下爆炸对应的封闭爆当量，文献［10-12，14］通过不同埋深处的爆炸试验，给出了不同介质中的当量耦合系数随比例埋深的变化曲线。

（3）地冲击参数耦合系数ησ，定义为相同介质、相同当量、相同爆心距情况下地下爆炸地冲击参数与封闭爆炸地冲击参数之比［5］，即

式中：σ、v、a、u分别为地冲击应力、粒子速度、粒子加速度以及介质位移；下标h与c分别代表比例埋深为hˉ以及封闭爆炸的情况。

美国工程兵水道试验站给出了混凝土和土中化爆的地冲击参数耦合系数曲线［5］，文献［10-12，14］通过试验得到了不同介质中的应力、加速度耦合系数曲线。

（4）填塞系数m，定义为相同介质，相同爆炸当量条件下，地下爆炸压缩半径与接触爆炸压缩半径之比，即

根据定义，上述前3 种耦合系数在封闭爆炸时等于1，非封闭时小于1；填塞系数m在接触爆炸时等于1，在封闭爆炸时为大于1的常数。

国内外上述几种表述的耦合系数曲线主要由试验得到，系数之间关系不清，适用范围受介质所限。为此，本文通过理论揭示耦合地冲击机理，阐明上述耦合系数之间的关联性，并提出便于防护工程应用的当量耦合系数和填塞系数计算方法。

2 地下爆炸地冲击耦合系数计算理论

2.1 地冲击能量计算

首先研究封闭爆炸与接触爆炸的地冲击能量与破坏区体积的关系。对于封闭爆炸，计算简图如图1c所示，可视为处于无限均匀介质中。在弹性区内，爆炸引起的介质运动可以看作是半径为r的球面扩张问题。在r处介质径向应力为σr，半径为r的球面相当于一个能量“源”，从球面辐射出的能量完全等于球面上介质应力所做功。由此可得辐射能量为

式中：Sr= 4πr2为半径为r的球面表面积；ur为r处介质的径向位移；ur(∞)为时间趋于无穷时的最终位移。

积分式（5）后可得到两项，分别代表介质的静态弹性势能与向远处传播的动能。地冲击能量指的就是介质运动动能，可写为［17］

式中：B*=[5+3(1+24ν)2]/64，ν为介质泊松比；τs为介质剪切强度；G为介质剪切模量；cp与cs分别为介质的纵波波速与剪切波速；Vpc=4πr3pc/3 为破坏范围边界所包围介质体积。

对于接触爆炸，计算简图如图1a所示，爆心上方的能量耗散至空气中，地冲击能量仅存在于爆心下方的半空间范围，因此有效能量与全部能量相等。

爆心下方破坏区范围为rp0，地表水平面上破坏区半径为rp*，假设破坏区边界截面为抛物线［15］，则可得爆心下方破坏区边界面积为

耦合能量计算式（5）的本质是将单位面积能量流对破坏区边界面积进行积分。对于任意形状的破坏区表面，可将其按面积等效为半球面［18］，因此对于式（7），有Sp0=4πrp0rp*/3=2πrˉp02，rˉp0为等效半球半径，可得接触爆炸向下传播的地冲击能量为

式中：Vp0=2πrˉ3p0/3。

由式（6）和式（8）可知，封闭爆炸和接触爆炸的地冲击能量与破坏体积成线性关系，单位破坏体积的能量相等，且为仅与介质性质有关的常数。

综上可知，对于比例埋深为hˉ的地下爆炸，破坏半径rph介于rpc和rp0之间，破坏体积Vph介于Vpc和Vp0之间，因此地冲击能量Wsh介于Wsc与Ws0之间。

封闭爆炸的压缩半径与破坏半径一般呈线性关系。但对非封闭爆炸而言，自由面的影响加大了破坏范围，根据文献［19］的研究，压缩半径ra与破坏半径rp的关系为

式中：θ为介质参数。

从式（9）可以看出，rp与ra的比值存在尺度放大效应。

2.2 地下爆炸耦合系数的理论表征

2.2.1 全部能量耦合系数与有效能量耦合系数

根据公式（1），结合公式（6）和（8），全部地冲击能量耦合系数ηet表述为

式中：0.5 ≤ξ≤1.0，为随埋深变化的系数，表征地下爆炸破坏区封闭度。

接触爆炸时破坏区可等效为半球，ξ=0.5；封闭爆炸时为完整球形，ξ=1.0。

有效地冲击能量耦合系数ηef表述为

式中：WshL与VphL分别为比例埋深hˉ处地下爆炸爆心下方半空间的地冲击能量和破坏区等效半球体积。需要注意的是，非封闭爆炸的有效地冲击能量WshL不等于全部地冲击能量Wsh的一半，因为地冲击在爆心上下半空间内不是均匀分布的。

由公式（10）、（11）可知，对于接触爆炸，有效地冲击能量耦合系数为全部地冲击能量耦合系数的两倍。

若将破坏半径换算成压缩半径，由公式（9）可将公式（10）和（11）分别改写为

2.2.2 当量耦合系数与能量耦合系数的关系表征

量纲分析与试验均表明［20-22］，爆炸成坑体积V与 爆 炸 当 量Q为 指 数 关 系，V=kQα，α=0.75～1.00，k为比例系数，由此推得压缩半径与爆炸当量的关系为ra∝Qα/3，从安全的角度，可取α=1.00。结合式（2），可将式（12）、（13）分别转化为以下当量耦合系数的形式：

由公式（14）、（15）可知，若不考虑公式（9）地下爆炸破坏区的尺度效应，则有效地冲击能量耦合系数ηef与当量耦合系数ηQ是一致的，即ηef=ηQ。

2.2.3 地冲击参数耦合系数与当量耦合系数的关系

对于封闭爆炸，地冲击可按下式计算［4］：

式中：vpk为粒子速度峰值；A与n为参数，可由试验确定。

地冲击应力可写为

式中：ρ0为靶体初始密度。

对于浅埋爆炸，根据式（2）的定义，地冲击可写为

或者根据式（3）的定义可写为

联立式（18）、（19），结合式（2）可得

2.2.4 填塞系数与当量耦合系数的关系

填塞系数是压缩半径之比，由式（4）与式（15）可得，填塞系数m与有效能量耦合系数ηef，以及与当量耦合系数ηQ的关系为

式中：ηef(0)、ηQ(0)分别为埋深为0时的有效能量耦合系数和当量耦合系数

综上可知，几种耦合系数之间均存在转换关系，且均与破坏体积密切相关。当量耦合系数、地冲击参数耦合系数以及填塞系数均是按有效地冲击能量计算。

3 耦合系数计算方法

针对接触爆炸和封闭爆炸破坏范围的研究已取得较为丰硕的成果，尽管目前在理论上尚难得到耦合系数随比例埋深的解析规律，但试验和数值模拟表明，能量耦合系数的演化轨迹类似Boltzmann函数的形式。图3 给出了一条完整的Boltzmann 函数曲线，对比图2 可以看出，耦合系数曲线与Boltzmann函数曲线的右半部分变化规律一致，通过调整具体系数大小可以改变曲线的初始值和增长速率。

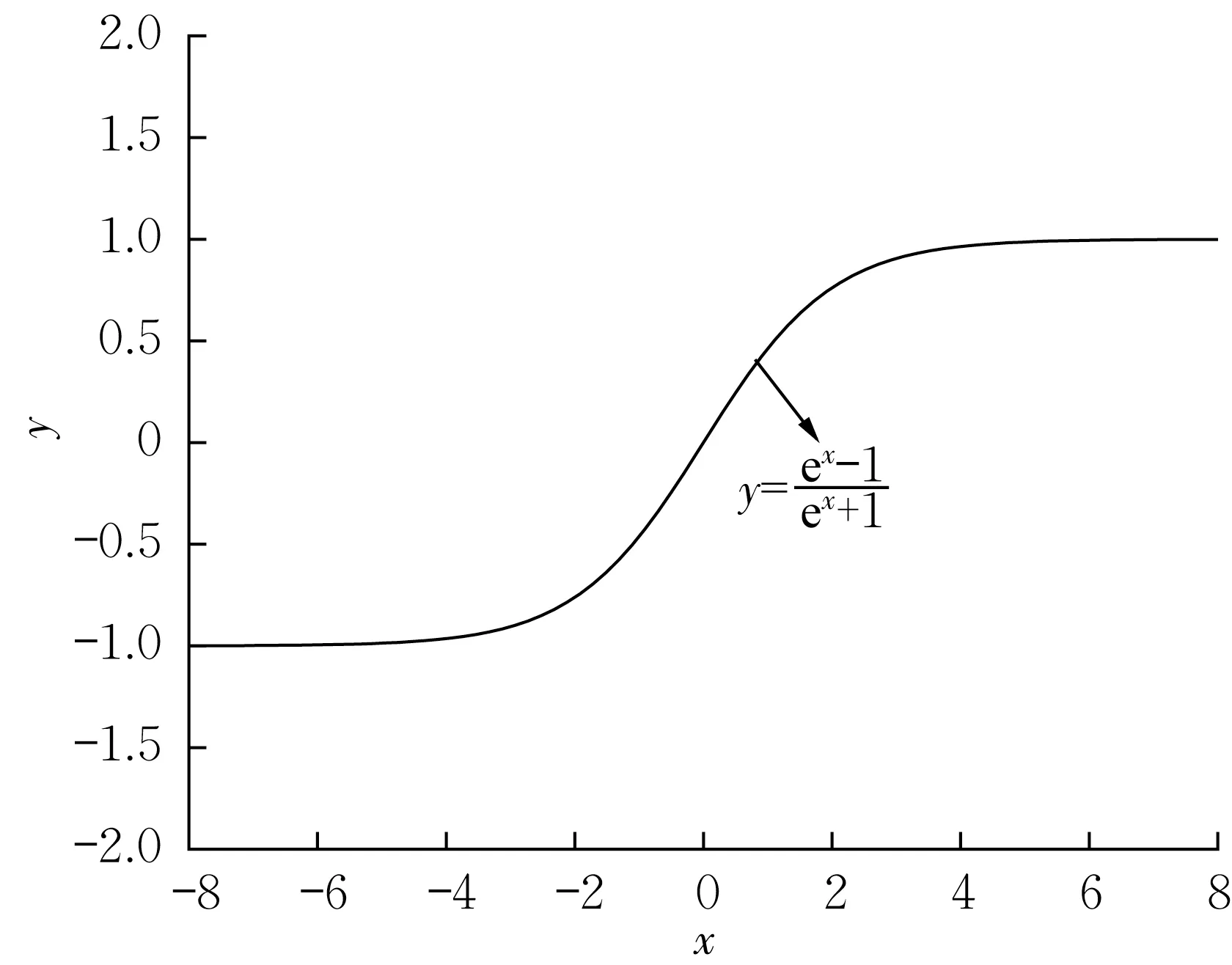
图3 Boltzmann函数曲线Fig.3 Curve of the Boltamann function

因此，可以将能量耦合系数ηe（实际计算中，ηe可取全部能量ηet或有效能量ηef）表达为

可以将ηe=0.99时看作达到完全耦合，将其代入式（22）可得

地冲击源自于爆炸空腔的扩张，当空腔扩张停止后，爆炸能量基本完成了耦合入介质的过程。当爆炸成腔在抛掷成坑之前完成时，可忽略自由面对地冲击耦合的影响，满足该条件的最小比例埋深约等于封闭爆炸压缩半径，即≈rac。大量抛掷爆炸试验充分证实了该结论［4］。因此，式（23）可写为

综上，确定式（22）仅需接触爆压缩半径和封闭爆压缩半径这两个参数。

根据美、俄数值模拟数据和试验数据，封闭爆的有效地冲击能量大约是接触爆的16 倍，则D1= 1/16 = 0.062 5，即ηef(0)=0.062 5，由公式（15）可得，封闭爆压缩半径是接触爆的2 倍。根据室外现场试验数据［4］，硬岩中封闭爆炸压缩半径为8～12 m·kt−1/3，可取10 m·kt−1/3，代入式（24），可得D2=1.9，由此可得有效能量耦合系数随深度变化的曲线。同理，根据式（15）换算可得有效能量耦合系数曲线，与美国根据数值模拟得到的曲线［3］和俄罗斯根据试验得到的曲线［4］进行比较，结果见图4。由图4可以看出，理论计算曲线总体介于试验和模拟曲线之间。比例埋深小于2.0 m·kt−1/3时，理论结果与俄罗斯试验数据吻合度更好；比例埋深大于2.0 m·kt−1/3时，理论结果更接近美国数值模拟数据。同时可以看到，全部能量耦合系数与有效能量耦合系数差距最大时是在埋深为0处，随埋深增加差距减小，最终均趋近于1。

图4 能量耦合系数理论计算结果与试验、模拟结果对比Fig.4 Comparison of theoretical energy coupling factor with experimental and simulation re⁃sults

利用式（15）将图4中的有效能量耦合系数曲线以及美国和俄罗斯的耦合系数曲线换算为当量耦合系数曲线，结果如图5 所示。由图5 可以看出，当量耦合系数计算曲线介于美、俄曲线之间，三者之间相互关系与能量耦合系数（图4）一致。

图5 当量耦合系数ηQ与美、俄曲线比较Fig.5 Theoretical ηQ versus curves of the United State and Russia

由式（21）将有效能量耦合系数曲线换算为填塞系数曲线（图6），当比例埋深为6.7 m·kt−1/3时，填塞系数为1.97，当比例埋深为10.0 m·kt−1/3时，填塞系数为2.00，表明比例埋深到6.7 m·kt−1/3时已可认为地冲击接近完全耦合，与美国结论一致。

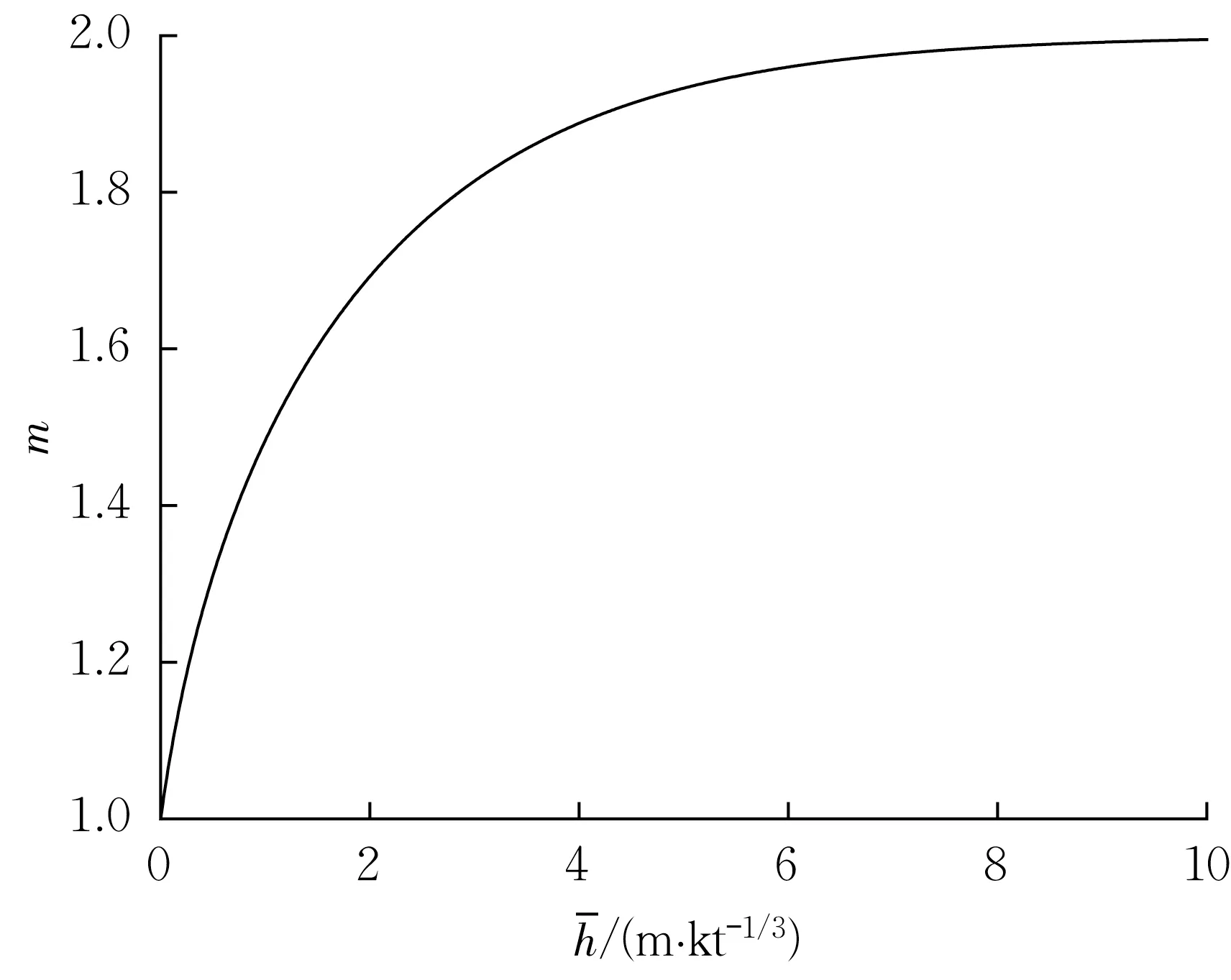
图6 填塞系数m计算曲线Fig.6 Calculated curve of packing factor m

为便于工程应用，可将图5当量耦合系数与图6填塞系数分别表达成如下关系：

4 结论

本文探讨了地下爆炸耦合地冲击等效计算理论和方法，得到如下结论：

（1）根据地冲击能量与爆炸破坏区的关系，得到了能量耦合系数（全部能量耦合系数和有效能量耦合系数）、当量耦合系数、地冲击参数耦合系数及我国规范使用的填塞系数之间的相互转换关系，若不考虑地下爆炸破坏区的尺度放大效应，有效能量耦合系数与当量耦合系数相等。

（2）通过Boltzmann 函数，利用接触爆和封闭爆压缩半径两个初始参数，可以得到耦合系数曲线计算公式。对于不同介质，封闭爆压缩半径已有大量理论和试验结论，而接触爆压缩半径仍需进一步理论分析和试验补充。

（3）通过与美、俄地下核爆耦合系数曲线对比分析，可以看出当埋深较小时耦合系数理论值与俄罗斯曲线较接近，埋深较大时与美国曲线较接近。结合填塞系数计算，美国给出的耦合系数曲线具有较好的可靠性，且偏安全。

作者贡献声明：

徐天涵：初稿撰写，理论推导，稿件修改。

邱艳宇：文献查找，理论推导。

谢 方：文献查找，理论推导，初稿校对。

王明洋：提出选题，写作指导，内容把关。