基于改进灰狼优化算法的含分布式电源配电网无功优化

海涛，杜松霖，葛思扬

（1.广西大学 电气工程学院，广西南宁，530000；2.南方电网电力科技股份有限公司，广东广州，510080）

0 引言

为改善化石能源对自然环境的污染，同时响应国家“双碳”和“十四五”能源规划，需大力发展以新能源为主体的新型电力系统。从而推动分布式电源(Distribute Generator, DG)快速化、规模化发展[1]。随着DG 大规模、高密度地接入，配电网的原有结构、潮流和电压分布发生改变，会增大网络损耗和降低电压质量，从而影响配电网运行的安全性和稳定性[2～3]。在含DG 的交流配电系统的网络损耗和电压优化问题方面已有一定研究基础[4]，无功优化则是其中一大热点。

无功优化的常见手段是控制静态无功补偿装置(Static Var Generator, SVG)的切入容量，这是一个多目标、多约束的非线性规划问题。传统数学优化法存在算法复杂度高、收敛性不足等缺点[5～6]。因此，研究人员引入智能优化算法来解决。文献[7]针对配电网无功优化的特点,提出一种基于局部电压稳定指标分区与改进粒子群算法相结合的配电网无功优化方法。文献[8]提出一种引入冯诺依曼拓扑结构的改进鲸鱼优化算法求解无功优化问题。文献[9]采用最优场景法模拟DG 和负荷的随机性进行无功优化问题建模，并提出一种改进人工蜂群算法求解。文献[10]建立了考虑风电、光伏的随机概率出力的无功优化模型，出一种基于改进元胞差分算法的配电网无功优化方法。

灰狼优化算法 (Gray Wolf optimization, GWO)是一种模拟灰狼群体捕食行为的智能优化算法，其结构简单、调节参数少，有着较好的求解精度和收敛速度，已应用于故障诊断、功率预测等诸多领域。与其他智能优化算法类似，GWO 算法仍存在种群多样性低、易陷入局部最优等缺点。

鉴于上述问题，本文首先分析含分布式电源的配电网系统，建立以有功网损和电压越限偏差最小为目标的无功优化模型；然后融合Sobol 序列、非线性收敛因子、黄金正弦优化算法和贪婪策略，提出一种改进GWO 算法；最后以增强式IEEE 33 节点配电网系统作为算例，对所建立无功优化模型和所提改进算法进行仿真分析，验证其可行性和优越性。

1 配网无功优化模型

■1.1 设备并网模型

本文设配电网系统中并入分布式光伏电源、分布式风能电源，通过控制SVG 补偿无功出力实现无功优化。以上三种设备在潮流计算中均可视为负输出的负载。参考并网等效计算方法，其并网模型可分为两类：

(1)PQ 节点

分布式风能电源和SVG 在运行过程中功率因数恒定，在潮流计算中可等效为PQ 节点，其计算模型可表示为：

式中：Pflow、Qflow分别表示潮流计算时的等效有功出力和无功出力，inP表示分布式电源注入有功，Qin表示分布式电源或SVG 的注入无功。

(2)PI 节点

分布式光伏通过直流逆变器并入配电网，其有功出力和注入电流恒定，在潮流计算中视为PI 节点，其计算模型可表示为：

■1.2 目标函数

(1)有功网损

有功网损指电能输送过程中以热能形式散发的有功功率损失，减小有功网损可以有效提升配电网运行的经济性，其数学模型可表示为：

式中：Ploss表示有功网损，n表示配电网系统节点数，Γ 表示能与节点i连成支路的节点j的集合，Gij表示节点i、j之间支路的电导，Ui、Uj分别表示节点i、j的电压幅值，ijθ表示节点i、j之间支路的相位差。

(2)电压越限偏差

节点电压越限可能导致设备无法正常运行甚至局部故障，带来安全隐患。减小电压越限偏差量能提高配电网系统运行的稳定性和安全性，其数学模型可表示为：

式中：1λ、2λ表示权值，本文取λ1=0.3，λ2=0.7。

■1.3 约束条件

(1)等式约束

潮流计算时，系统各节点的有功功率和无功功率相等，表示为：

式中：Pi、Qi分别表示节点i处有功负荷和无功负荷，Bij表示节点i、j之间支路的电纳。

(2)不等式约束

本文选择SVG 的出力作为控制变量，需考虑其出力阈值，表示为：

2 GWO 算法及其改进

■2.1 GWO 算法简介

GWO 算法模拟构建了灰狼群体的社会等级分层。把每一个灰狼个体看作一个问题的解，并将种群中求解适应度最好的三个灰狼个体依次标记为α、β、δ，其余标记为ω。灰狼群体狩猎过程如下：

(1)包围猎物

灰狼群体发现猎物后，会逐步包围猎物，其数学模型表示为：

式中，tmax表示最大迭代次数。

(2)捕食猎物

在实现包围后，ω狼在α、β、δ狼的带领下捕食猎物，其数学模型表示为：

■2.2 对GWO 算法的改进

GWO 算法存在后期全局搜索能力差、易陷入局部最优以及收敛速度较慢等问题，本文采取多种策略改进原算法，提出一种改进GWO 算法(IGWO)。

2.2.1 改进种群初始化

对于解分布未知的优化问题，若采用随机序列产生初始，可能使最优解附近个体分布稀疏，劣等解附近个体分布集聚，影响求解效率。

Sobol 序列是一种低差异序列，能通过合理的采样方向将样本尽可能均匀地填充在样本空间内，在处理概率问题时具有更高的优越性。

为对比随机序列和Sobol 序列产生的初始种群，分别用两种序列在取值范围为，维度为2 的样本空间中产生100 个样本，结果如图1 所示。

图1 使用不同序列产生样本

由图1 可得，相较于随机数序列，通过Sobol 序列产生的初始种群分布更均匀，遍历性更高，有利于提升算法求解效率。

2.2.2 改进收敛因子

在GWO 算法中，A用于指示算法进行全局搜索或局部搜索。由式(11)可知，A随着收敛因子a变化而变化。由式(13)可知，a随着迭代次数线性减小，但算法的迭代搜索过程是非线性的，a线性递减会导致算法后期的全局搜索能力较差，易陷入局部最优。因此，本文引入余弦函数构造非线性收敛因子，表示为：

式中：aini、afin分别表示a的初始值和终止值，在本文中，aini=2 ，afin=0 。

非线性收敛因子随迭代次数的变化情况如图2 所示。

图2 不同收敛因子迭代变化曲线

由图2 可得，非线性收敛因子在算法前期变化速率慢，能更好地适应算法的全局搜索，在算法后期变化速率快，能提高算法局部搜索的效率。因此，非线性收敛因子可以有效平衡算法的全局搜索和局部搜索能力。

2.2.3 改进位置更新策略

黄金正弦优化算法(Golden sine algorithm, Gold-SA)根据正弦函数与单位圆的关系，可以遍历正弦函数上的所有值，即寻遍单位圆上所有的点，同时在其位置更新过程中引入黄金分割数缩小解决方案的空间，以便扫描产生优质解概率大的区域，很大程度上提高了搜索速度，且使搜索和开发达到良好的平衡。其数学表达式如下：

将Gold-SA 算法的位置更新策略融合进GWO 算法中，通过比较个体适应度选择位置更新策略；同时采用贪婪策略判断是否更新当前个体，当新个体适应度优于当前个体时更新，否则就保留当前个体，以增强算法的求解效率。其改进的位置更新策略表示如下：

3 无功优化算例分析

■3.1 含DG 配电网无功优化流程

综上所述，本文所提及基于改进GWO 算法的含DG 配电网无功优化流程如图3 所示。

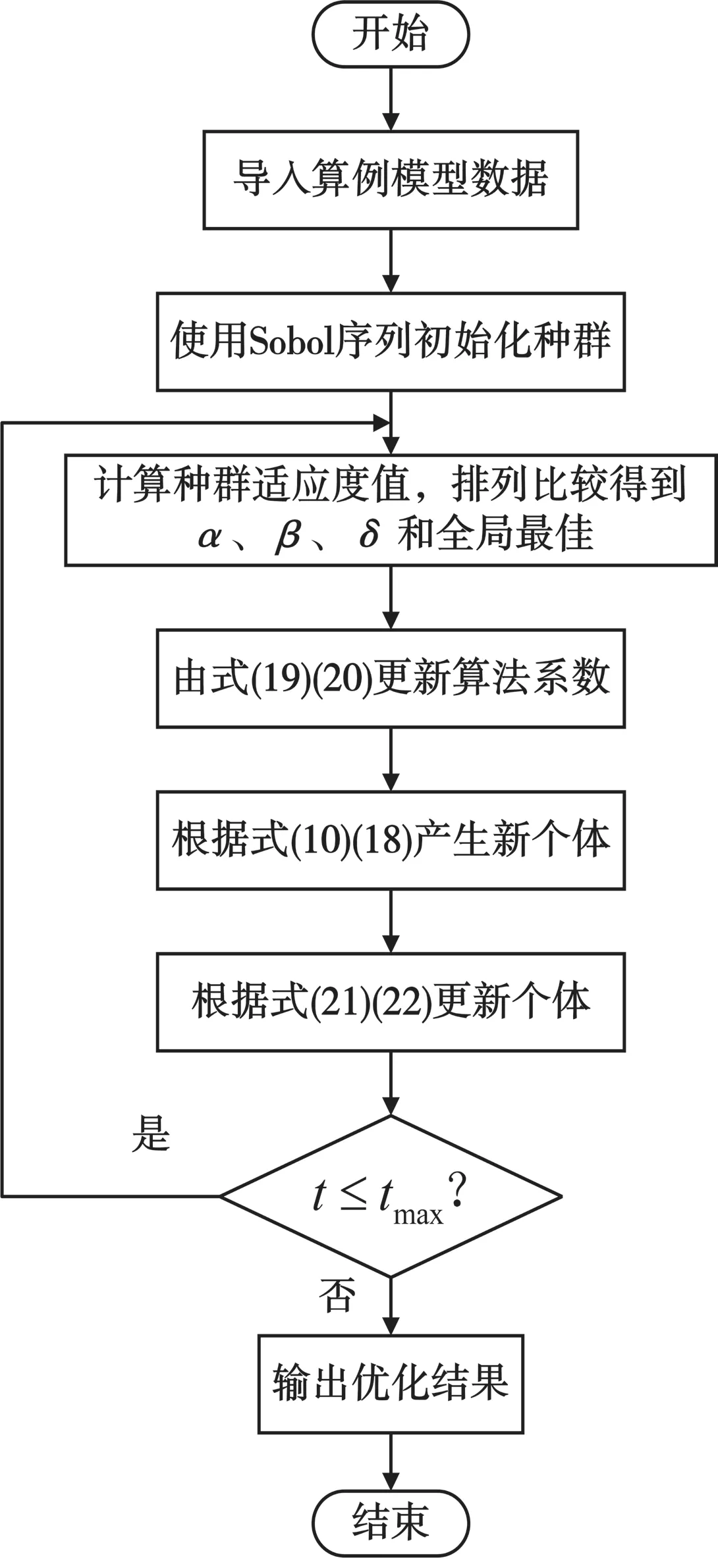
图3 含DG 配电网无功优化流程框图

■3.2 测试系统参数

本文选取增强式IEEE 33 节点系统作为算例，基准电压为12.66kV，其结构如图4 所示。光伏电源接入节点18、33，其最大有功出力为0.4MW，注入电流为50A；风能电源接入节点22、25，其最大有功出力为0.3MW，功率因数为0.88；SVG 接入节点18、22、25、33，其最大无功出力为1.5Mvar。

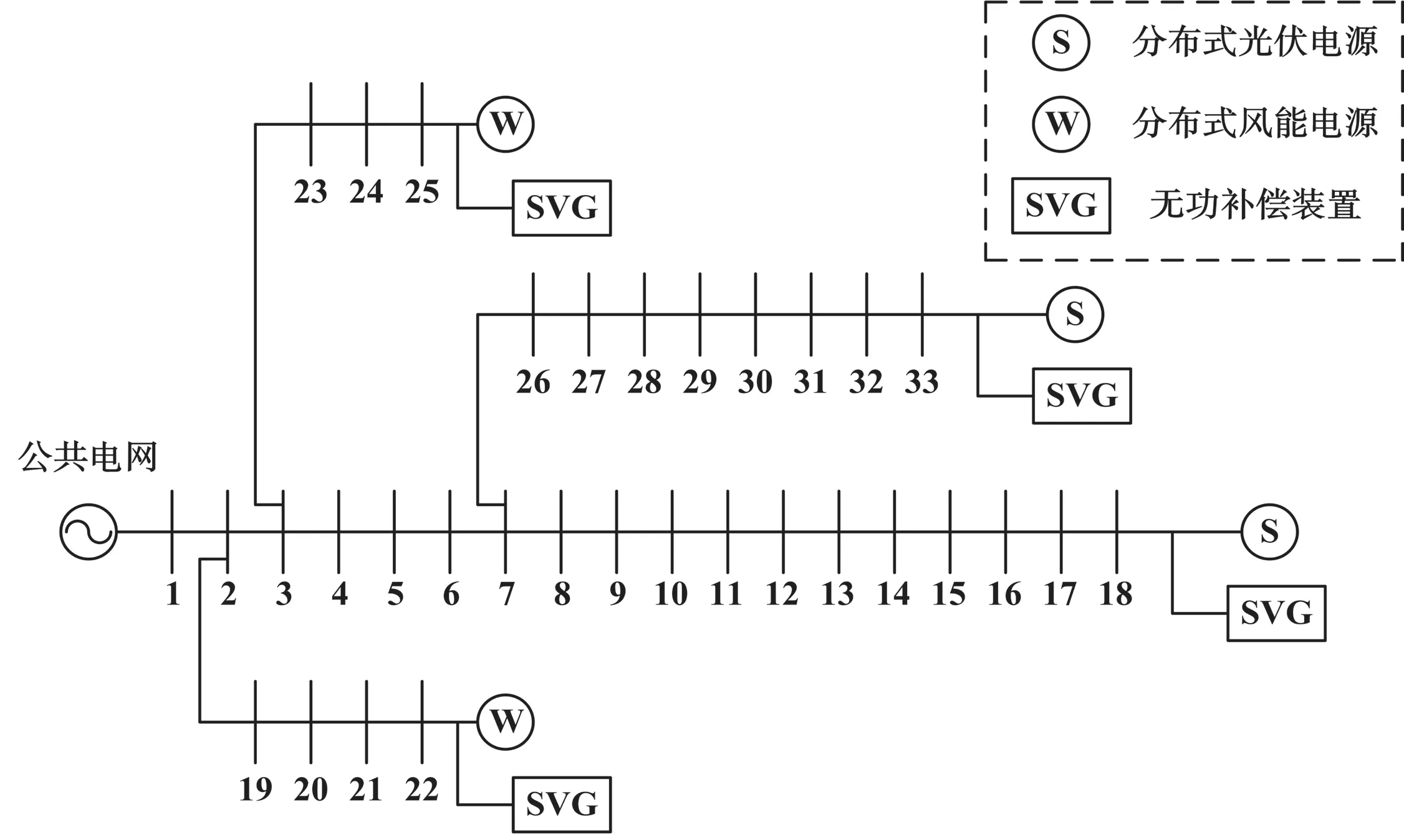
图4 增强式IEEE 33 节点系统

以1h 为采样步长，系统的日有功负荷和DG 日有功出力情况分别如图5 和图6 所示。

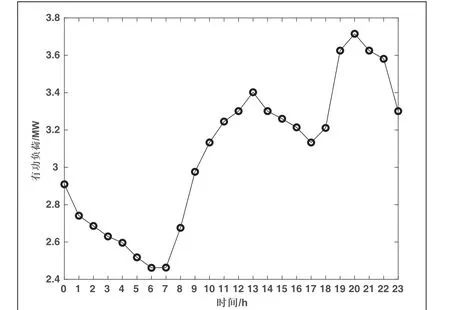
图5 增强式IEEE 33 节点系统日有功负荷曲线

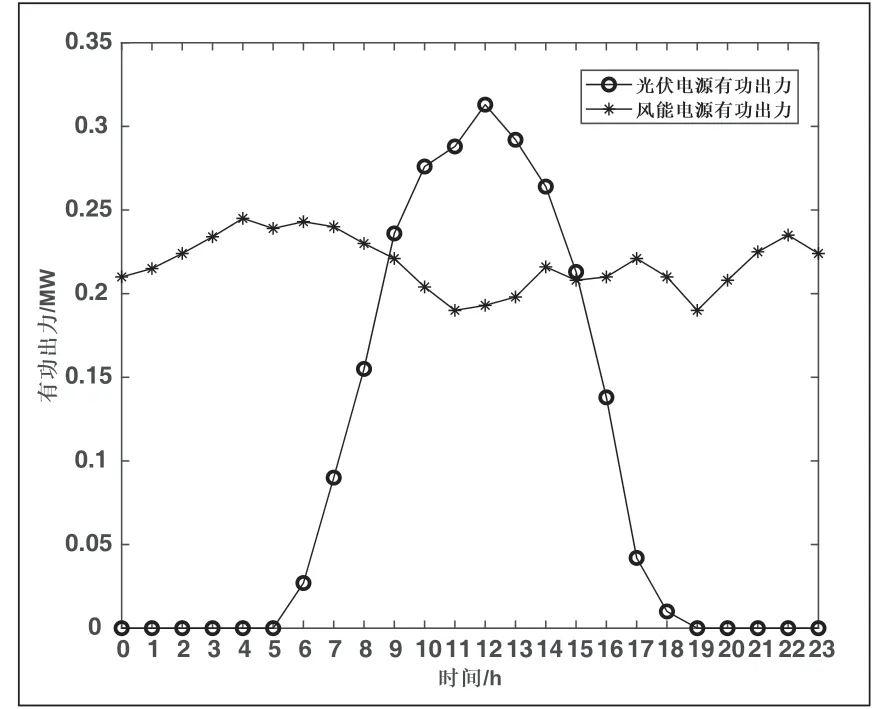
图6 增强式IEEE 33 节点系统电源日有功出力曲线

■3.3 仿真结果与分析

3.3.1 算法性能测试

为验证IGWO 算法优化性能的优越性，在算例中分别独立应用GWO 无功优化策略（以下简称“GWO 策略”）和IGWO 无功优化策略（以下简称“IGWO 策略”）。设最大迭代次数均为80 次，其仿真结果如图7 所示。

图7 有功网损迭代曲线

在求解精度方面，系统未引入无功优化策略时的总体有功网损为2426.01kW，分别引入GWO 策略和IGWO策略，系统稳定后的总体有功网损分别为806.93kW 和795.97kW。IGWO 算法的求解精度相较于GWO 算法更高。

在迭代速度方面，IGWO 策略能在24 次完成迭代，而GWO 策略需要在63 次完成迭代。IGWO 策略的迭代速率明显高于GWO 策略，且迭代曲线平稳。

因此，在求解无功优化问题方面，IGWO 策略比GWO策略更具有优越性。

3.3.2 有功网损优化结果分析

将两种无功优化策略后的有功网损分别与未引入无功优化策略有功网损相比较，求得各时刻有功网损优化率如图8 所示。

图8 各时刻有功网损优化比

式中：R表示有功网损优化率，Pini表示未引入无功优化策略时的有功网损，Pop表示引入无功优化策略后系统稳定时的有功网损。

由图8 总体上看，IGWO 策略在各时刻的有功网损优化水平略优于GWO 策略。IGWO 策略最大有功网损优化率为70.11%，最小为59.44%；GWO 策略最大有功网损优化率为70%，最小为59.22%。当配电网系统容量增大时，IGWO 策略优化有功网损的量相较于GWO 策略将获得可观的提升。

由图5 可得，系统用户侧用电有两个高峰时段，为7～13 点和17～21 点，结合图8 可得，IGWO 策略在两个用户侧用电高峰时刻的有功网损优化情况优于GWO 策略，说明IGWO 策略处理高峰时段的能力优于GWO 策略，有利于支撑配电网在高峰时期的运行能力。

3.3.3 电压偏差优化结果分析

有图5 可得，21 点是一天中系统最大负荷时点，其未引入无功优化策略和分别引入两种无功优化策略后的节点电压的变化情况对比结果如图9 所示。

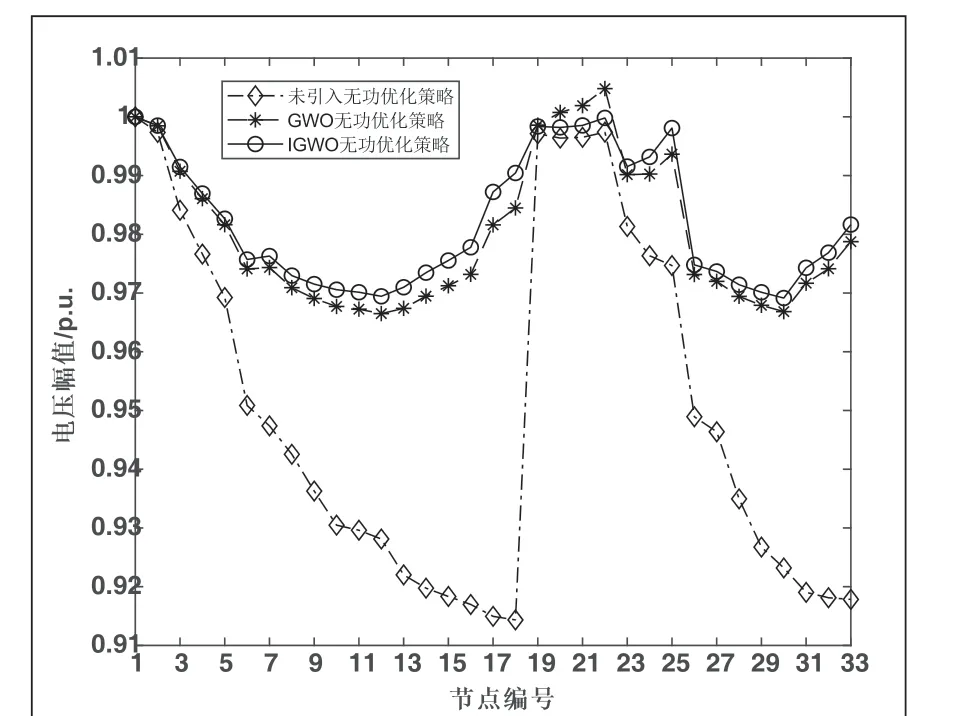
图9 21 点各节点电压变化情况

由图9 可得，未引入无功优化策略时，配电网系统的电压在节点18 达到最低值0.914p.u；引入GWO 策略后，系统电压在节点12 取得最低值0.967p.u.，在节点18 抬升至0.985p.u.；引入IGWO 策略后，系统电压在节点30 取得最低值0.969p.u.，在节点18 抬升至0.990p.u.。IGWO策略相较于GWO 策略对节点电压最低值的抬升效果更好，能更好解决电压跌落情况。

为验证节点电压优化的普适性，本文选取节点16 作为研究对象，其在未引入无功优化策略和分别引入两种无功优化策略的各时刻节点电压变化情况如图10 所示。

图10 节点16 各时刻电压变化情况

由图10 可得，IGWO 策略和GWO 策略在各时刻对节点电压均有抬升作用。未引入无功优化策略时，节点16在20 时取最低电压0.919p.u.；引入GWO 策略后，节点16 在20 时取最低电压0.972p.u.；引入IGWO 策略后，节点16 在21 时取最低电压0.978p.u.，在20 时抬升电压至0.979p.u.。因此，IGWO 策略相较于GWO 策略对最低电压抬升效果更明显。对整体而言，IGWO 策略对节点电压的优化效果更加平稳，更能有效减少电压情况，确保配电网系统稳定安全运行。

4 结论

本文以有功网损和电压越限偏差最小为目标，融合Sobol 序列、非线性收敛因子、黄金正弦优化算法和贪婪策略，提出一种IGWO 算法应用于解决DG 并网无功优化问题。通过分析算例仿真结果可得，所提IGWO 算法组成的无功优化策略，能降低配电网的总体有功网损和电压越限偏差，提高系统电能质量。相较于传统GWO 算法，IGWO 算法拥有更好的优化效率。

同时，本文所提改进算法有利于制定更优质的无功优化策略，减小DG 并入配电网后的不利影响，提高系统运行的稳定性、安全性和经济性，为后续解决含DG 的配电网系统的优化问题提供了进一步的借鉴和参考。