基于FPGA 的模拟欠光环境下图像边缘检测系统的设计与实现

王相超，陈龙，颜斌

（杭州电子科技大学 电子信息学院，浙江杭州，310018）

0 引言

图像的边缘，也称图像轮廓，是一种重要的视觉信息。作为图像分析处理、计算机视觉的基本步骤，图像边缘检测结果的准确性将直接影响到机器视觉系统对客观世界的理解[1]。在机器视觉领域，图像边缘检测常用的算子包括Sobel 算子，Canny 算子，Prewitt 算子和Robert 算子[2]，各类算子针对不同情景，其使用各具优势。其中，Sobel 算子较其他算子有更高的边缘检测精度和抗躁能力，对于各类图片边缘检测有较强的泛化能力和鲁棒性而被广泛应用[3]，但传统的X，Y 两方向的Sobel 算子对图像边缘信息的提取能力仍然有限，在检测水平、竖直以外方向的边缘信息时，容易引入噪声或检测失败[4-5]而降低识别准确率。同时，无论边缘检测算法使用哪种算子，其先决条件都是图像本身要清晰可辨，算法对待处理图像的光照条件，明亮程度有一定要求。当待处理图像总体色度偏低，光照条件不足或者光照分布极其不均匀，应用边缘检测算法得到的识别准确率将大大降低[6]。由此，本文提出了一种在FPGA 平台搭建的，基于直方图增强与8 方向Sobel 算子的图像边缘检测系统，能够快速，准确地提取缺乏光照条件下所拍摄图片的边缘信息。

1 算法原理分析

■1.1 直方图均衡化

直方图均衡化则是一种用于增强动态范围偏小图像的对比度的算法。图片拍摄时光照过强过弱在其灰度统计直方图上的反映：灰度集中于高亮部分和低亮部分，如图1 所示，图片整体色度偏暗，统计直方图所含灰度值频次集中于低灰度部分，图片中诸如人脸轮廓，前景与背景差等细节部分难以突出。对于此类图片使用直方图均衡化算法，可以将灰度图像的直方图分布重新映射为均匀分布，增强图像对比度从而使图像细节信息更为突出[7]，如图2 所示。

图1 低色度图片与直方图

图2 直方图均衡化结果

直方图均衡化基于对灰度图像的统计直方图，以256灰度级图像为例，所谓统计直方图，就是遍历灰度图每个像素，统计每个像素灰度级的出现频次，数学表达如式1，ni为灰度值i 对应的出现频次，N 为图像总像素数。

而直方图均衡化本质是改变灰度值的概率分布使其成为均匀分布，需要借助变换函数对原分布进行操作。由概率论理论推导可知，以函数P 的累积分布概率函数作为变换函数Sk，其分布满足均匀分布，数学表达如公式2。

因此，在原统计直方图的基础上，对频次进行累加，得到图片累计直方图，该分布即为直方图均衡化的目标函数，而累计直方图得到的结果是灰度级累计概率，因此需要将结果乘总灰度级个数完成映射。

■1.2 8 方向sobel 边缘检测算法

图像的边缘是指其图像灰度值或纹理结构等信息的突变位置，而Sobel 算子在设计原理上为一阶离散差分算子，为大小固定的方阵。算子通过与图像子模板的卷积运算[8]（式3）可以计算灰度图像的近似梯度值。

经典的Sobel 边缘检测算法包括水平X 方向与竖直Y方向两个算子，算子常选用的模板尺寸为3×3，如图3 所示。X 方向算子以中间列作为基准，计算左右两列卷积的差值，在计算机中，差分运算等价于微分运算，即可求出图片X 方向梯度值。Y 方向运算同理。最终将X，Y 方向得到的梯度信息进行求和，与设定的阈值相比得到边缘信息。

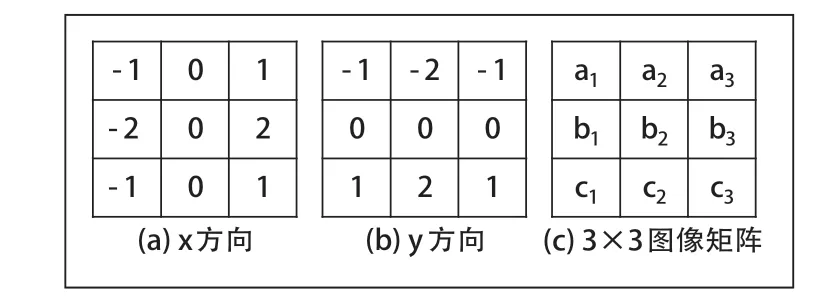
图3 传统Sobel 算子

经过图像灰度化与模板获取后，将每次计算得到的8 个方向的梯度值求平方和再开根号（式4），每个结果Out 与算法设定的阈值threshold 相比较进行二值化，获得图像边缘信息Edge（式5）。

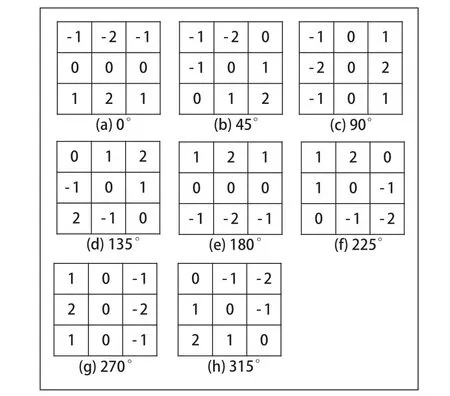
图4 8 方向Sobel 算子

3.3.1 图像3×3 模板获取

能源消费结构不断优化，与2015年相比，2030年煤、油比重分别下降15.2%和5.6%，天然气和非化石能源比重分别上升8.0%和12.8%[4-5]。

图5 算法流程图

由于传统的Sobel 算子仅计算水平与垂直两个方向的图像灰度梯度，会导致边缘检测不连续或不够准确。改进型的8 方向Sobel 算子较之传统算法，共使用到8 个方向Sobel 算子。一一对应于图像3×3 模板360°范围内的均匀划分空间。使算法能够充分地提取图像边缘信息[9]。算子模板如图4 所示。

The sun sets earlier in May and July, summer-rain is so much that people get sad.

2 系统总体结构设计与工作原理

系统使用Inter 公司旗下Cyclone 4 系列芯片—EP4CE10F17C8N 作为主控，普通逻辑资源丰富，拥有约10k 的逻辑单元。通过晶振电路可产生50MHz 方波，经过锁相环PLL 分频产生33.3MHz 时钟用于驱动VGA 显示屏。使用ROM 模块用于存储原始的BMP 图片，使用两个RAM用于进行灰度直方图统计与均衡化，使用若干按键用于显示系统各环节图像处理的结果。VGA 分辨率使用800×480。总体结构如图6 所示。系统仿真电路设计图如图7 所示。

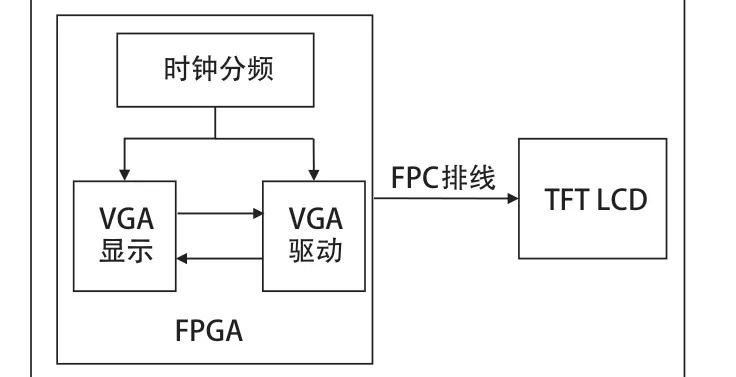
图6 系统总体结构图

图7 系统电路图

式中ram_data_sum 为累计直方图中灰度的累计频次，10000 为原图总像素数，255 为总灰度级。gray_s 为均衡化后的灰度值。

3 FPGA 模块化设计与仿真

■3.1 ROM 图像读取与放大

本系统使用FPGA 内置的ROM 模块对原始图片进行储存与读取，其集成电路如图8 所示。ROM 存储图片的mif 文件信息，模块包括两个输入端口，时钟输入与地址端输入，输出为对应地址的图片数据。

仿真波形如图10 所示。第一行为RAM 输入时钟，第二三行分别为原图灰度值与直方图均衡化后的灰度值。

图8 ROM 模块

图片mif 文件使用BMP2Mif 转换软件生成，原图为RGB888 格式的BMP 图片，生成mif 文件对应的输出数据大小为24bit。

由于系统自带ROM 模块进行数据存储的容量有限，最多可以保存200×200 大小的图片，影响结果观感。因此，设计了图片放大算法，输入图片为100×100，在显示时扩大至800×480。

第一行为原图像素灰度值，第二行为滤波后像素灰度值。

图片放大算法利用其显示原理，VGA 屏幕横坐标位置每8 个坐标单位显示实际图片的同一坐标信息，纵坐标位置每4.8个坐标单位显示实际图片同一信息，算法公式如公式6。

2.2 两组新生儿指标比较 观察组新生儿出生体质量、巨大儿4例(5.00%)，对照组分别为(3.81±0.73)kg和15例(18.75%)，差异有统计学意义(t=-8.33，P=0.02；χ2=21.60，P=0.00)；两组新生儿窒息率均为2.50%(2/80)，差异无统计学意义(χ2=1.31，P=1.24)。

式中rom_addr 为ROM 的输入地址，每个地址保存图片一个像素信息，pixel_xpos 为VGA 屏扫描的横坐标，pixel_ypos 为对应纵坐标。100 为输入图片的宽度。

■3.2 图像灰度化与直方图均衡化

3.2.1 图像灰度化设计

由于从ROM 中读取的为BMP 图片，如果直接进行边缘检测 则是对RGB 三通道色彩进行单独检测，但是各原色在同一像素位置的梯度大小方向可能各不相同，得到的边缘信息也不同从而发生检测错误。因此需要将图片转换为单通道，即灰度化。

RGB 灰度化公式如下：

而FPGA 进行浮点运算较为复杂，因此这里采取乘加与移位的近似计算。

rom_data 共24bit，每8bit 对应原图一个通道。完成了对原图的灰度化。

3.2.2 直方图均衡化设计

在设计上，系统使用两个单端口RAM 模块对数据进行存储来完成直方图与累计直方图的统计。RAM 模块集成电路如图9所示。

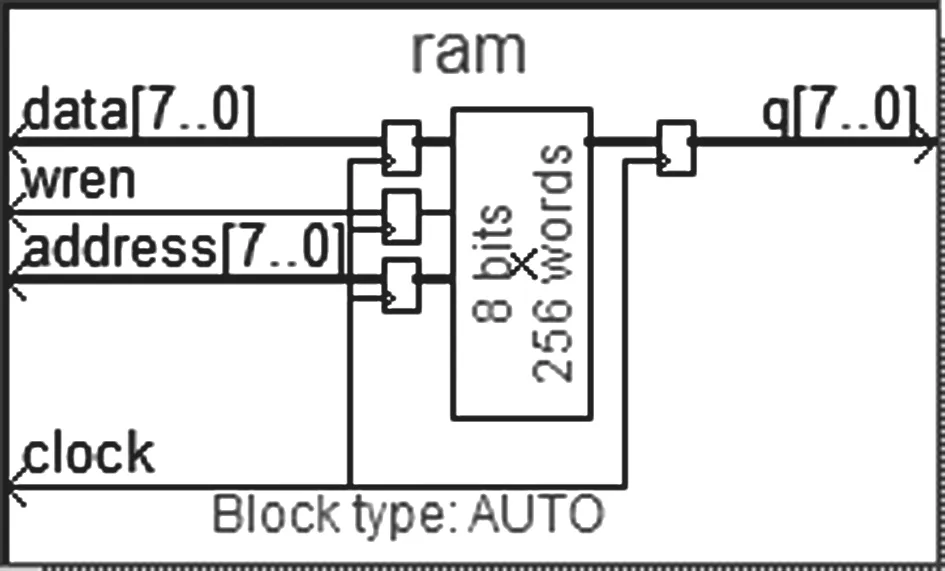
图9 RAM 模块

第一个RAM 用于对原始直方图进行统计，地址端从0～255依次遍历，当对应位置图像像素灰度值与地址匹配时，写入的data 数据自增1，当遍历完整幅图像也就完成了对原始灰度图的直方图统计。第二个RAM 用于计算累计直方图，当从RAM1 中读取的data 数据不为0 时，对写入数据进行累加，再通过归一化完成直方图均衡化（式9）。

系统经过初始化，首先从ROM 模块中读取存储的BMP图片，经过图像放大后进行灰度化处理，使用两个RAM 模块分别用于直方图统计与累计直方图计算，经过归一化处理后得到图像增强的结果，使用按键1 显示于显示屏上。使用高斯卷积核对增强图片进行滤波，结果使用按键2 显示。取滤波后的图像3×3 模板分别与8 方向Sobel 算子进行卷积，求出梯度和与阈值比较，得到边缘检测结果，使用按键3 显示。

但是，商业银行金融产品单一，而且创新效果并不理想，产品同质化比较严重，这些都是商业银行需要进行金融产品创新的重要原因。

图10 直方图均衡化仿真结果

图11 移位寄存器生成图像模板

■3.3 图像高斯滤波与Sobel 边缘检测

在确定所使用的算子后，边缘检测算法流程如图5 所示。

FPGA 中图像数据的保存形式是串行数据流，通过使用带taps 的移位寄存器模块，将串行数据转化为3×3 的模板数据。每次取图片3 个像素点信息于寄存器中，在第二个时钟到来时，间隔一行像素进行存储，重复三次即获得了图像3×3 模板数据。

移位寄存器模块仿真结果如图12 所示。

图12 图像模板仿真结果

3.3.2 图像高斯滤波实现与仿真

从图2可以看出，创作谢里丹风格唐草纹样，确定好主花位置，画出半径为3cm的圆，然后围绕主花利用sin曲线为基线绘制叶子，使叶子形成圆形的涡卷。以波状线与切圆线相组合，并向两个相反方向波卷，组成“S”形枝蔓连绵的纹样。圆圈是参考线，叶的线条尾端要自然地接近圆圈但不能相交。一直保持线的末端离圆圈1～2mm。叶片数量一般在8～10片。

与Sobel 原理类似，在获取图像3×3 模板后，在FPGA 上设计高斯卷积核，与模板进行卷积运算得到结果。系统设计时，卷积操作通过乘加器完成。经过高斯滤波，消除直方图均衡化对灰度图像带来的锐化噪声，提高边缘检测的准确率。

全面优化基于B/S架构的高校人力资源管理系统设计与实现方案，提升高校人力资源管理质量，首先要着重设计基于B/S架构的人力资源管理平台，充分发挥人力资源管理职能，从而有效提升本校的人力资源管理质量。目前，人力资源管理具备人力资源规划、招募与甄选职能，人力资源开发，薪酬福利管理，职业生涯规划，劳资关系管理和人力资源研究等六种职能，在构建人力资源管理平台的过程中，要紧密融合这六项职能，促进人力资源管理体系的良好发展。

高斯卷积核如图13 所示。

图13 高斯卷积核示意图

可以看出高斯滤波是对原图像模板各位置加权求平均值得到滤波结果。模板窗口滑动遍历整幅图片，得到高斯滤波结果。仿真结果如图14 所示。

图14 高斯滤波仿真结果

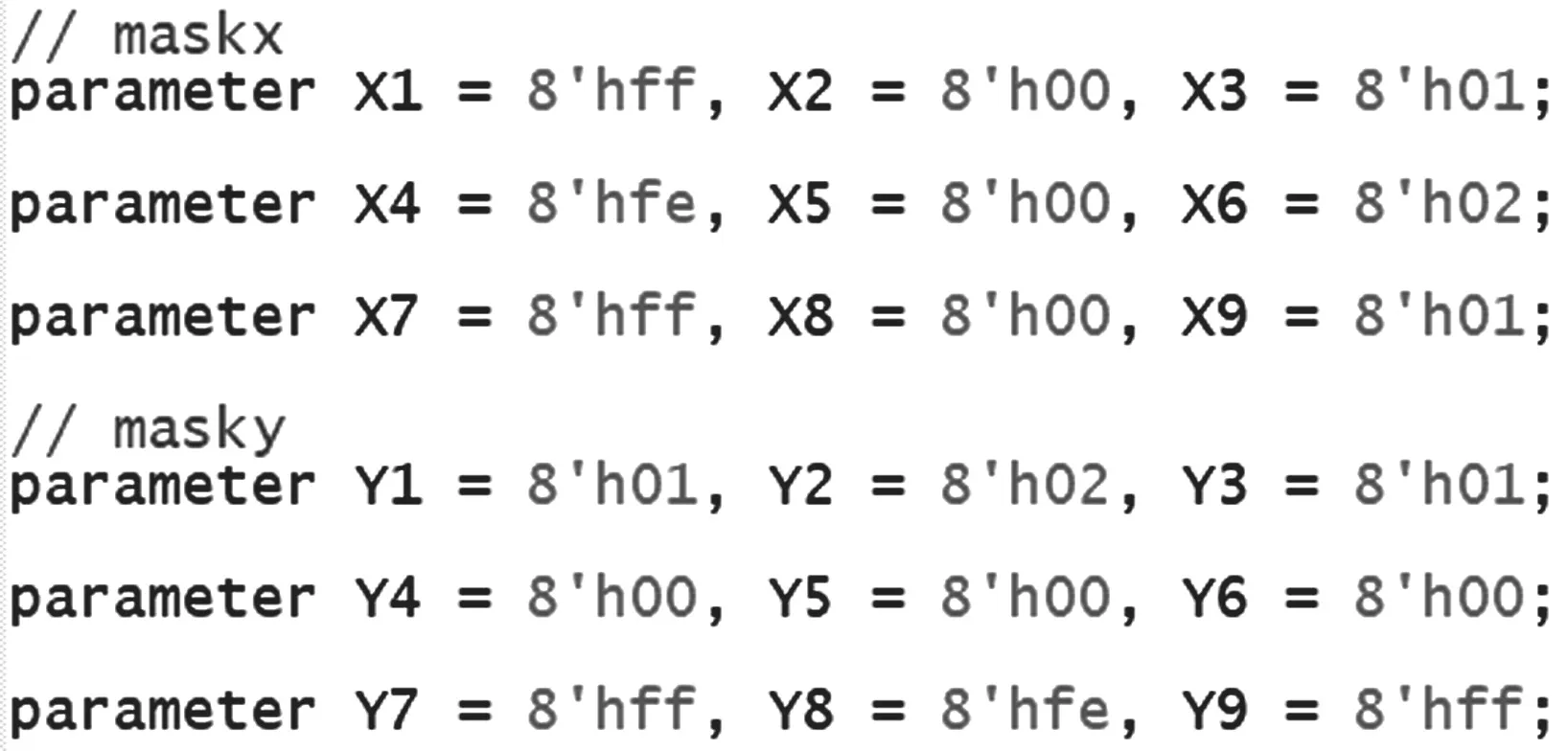
图15 Sobel 算子参数定义

从诺利地图到瓦齐城绘：18 世纪罗马微观城市空间的创新研究引介 黄健文 张伟国 徐 莹2018/04 57

3.3.3 Sobel 边缘检测与仿真

左小龙把摩托车停在一间酒店门口，琢磨着看大局这里超不过一百元一晚上。虽然所剩下的钱不多，但好歹比搞一个小姐便宜。到了前台，左小龙问：“多少钱？单人间。”

我站在这里觉得很尴尬，相比那些城里人，我总觉自己是个冒牌货。看打球的除了我，还有个坐轮椅的老头，他眼神怪怪地瞅着我，让我感到浑身不自在。

在获得滤波图像数据之后，同样使用移位寄存器，将滤波数据串行输入转换为3×3 的模板数据，再依次与8 个Sobel 算子进行乘加器卷积运算。需要注意的是，在8 个Sobel 算子设计时，其中的负数需要以补码形式定义。以90 度方向算子和180 度方向算子定义为例。

参数定义中的ff与fe 分别对应十进制的-1 与-2。

教工党支部的建设是一项系统化工程，发展历史较短的民办高校的党建工作，需要进一步解放思想，深入研究，研究建设民办高校教工党支部建设的新思路和新方法，不断提高民办高校教工党支部工作的针对性和实效性，充分发挥教工党支部的主体作用，为高等学校基层党组织的建设注入新的活力，开创新的局面。

与高斯滤波计算过程有差别的是。边缘检测算法还需进行梯度合成与阈值判断。梯度合成使用浮点运算单元中的开方运算器实现。最后，边缘检测仿真结果如图16 所示，1表示边缘信息，0 表示非边缘信息。第一行为系统时钟，每个时钟周期对应一个像素信息，从图片左上角至右下角，自左向右，自上向下遍历，第二行表示每个像素点是否为边缘信息。

图16 边缘检测结果仿真

4 系统实验结果分析

通过对系统整体结构的分析，设计了实验平台，编写verilog HDL 程序完成了ROM、RAM 存储读取，图像放大，图像灰度化，直方图均衡化，Sobel 边缘检测模块的实现。最后驱动VGA 显示屏显示结果。图17 为未经直方图均衡化的边缘检测结果。图18(a)为输入的原始低亮度图片，图18(b)为直方图均衡化后的灰度图，图18(c)为经过直方图均衡化与高斯滤波的图片，图18(d)为最终的边缘检测结果。

荸荠：购置于湖北省武汉市洪山区南湖大道菜市场。挑选大小均匀、无明显机械伤、无病虫害、成熟度一致的荸荠作为试验材料。

图17 直接边缘检测结果

图18 系统图像处理结果

可以从图17 与图18 的对比结果中可以看出，未经直方图均衡化增强而直接进行边缘检测，由于图片整体灰度值普遍低于阈值并且对比度低，细节信息非常少，难以识别出图片边缘。而经过直方图均衡化，图片对比度提升，图片可辨识度大大提高，系统可以较为准确地识别出边缘信息。

5 结语

本文针对图像边缘检测算法，关注于外界光线条件不足对算法结果的影响，设计了一款综合直方图均衡化图像增强，图像高斯滤波，8 方向Sobel 边缘检测的FPGA 图像处理系统。该系统相较于传统算法，能有效解决欠光环境下边缘检测可行性低的问题，大幅提升了算法对光照条件的鲁棒性，同时以FPGA 作为系统主控，提升了算法效率。结合了图片全局灰度均值作为阈值初值的方法，大大减少了在FPGA 平台搭建边缘检测算法的参数调整时间。后续可结合SDRAM 外设进行原始图片的存储读取以解决ROM 存储空间有限的问题，使原始图片具备更高的分辨率。