模型平均辅助抽样估计方法研究
2023-07-13陈茜儒贺建风
陈茜儒,贺建风
(1.广东金融学院 金融数学与统计学院,广州 510630;2.华南理工大学 经济与金融学院,广州 510006)
0 引言
随着现代信息技术的飞速发展,各行各业的平台系统规模迅速扩大,所产生的数据量呈现指数级增长,大数据已经成为经济社会的资源宝库。与此同时,大数据时代的到来也为抽样调查提供了更多可利用的辅助信息,这有助于提高估计精度。为了在抽样估计环节中利用辅助信息,传统的做法是建立研究变量和辅助变量之间的超总体回归模型,以此来调整和改进基于设计的随机化估计结果,这种方法被称为模型辅助抽样估计方法。其中,模型的构建及模型的拟合效果是决定这种方法能否改进随机化估计的关键之所在。因此,为推动大数据与抽样估计方法的融合发展,必须要考虑如何根据大数据下的辅助信息特征来构建合适的模型以进行辅助估计。
大数据背景下,辅助变量的一个重要特征就是数据维度过高,这导致在超总体建模过程中通常存在变量选择或模型选择的不确定性问题,进而影响模型辅助抽样的估计效果。在此特征下,如何利用多维甚至高维辅助变量进行抽样估计,是推动模型辅助抽样估计方法进一步发展亟须解决的技术难题。因此,需要综合考察模型拟合效果和模型简洁性以得到最优估计结果,同时应尽可能利用更多辅助信息提高模型辅助抽样估计效率。对于这类问题,一般有模型选择和模型平均两种方法,前者通常依赖数据驱动或者人为经验选择单一模型,后者则通过组合多个模型并对模型估计结果进行加权平均。模型平均方法一般不会把某个选定的模型当作真实的数据产生过程,而是通过合理的权重将所有模型考虑在内,这为模型估计提供了一种保障机制,有效规避了模型选择偏误[1]。因此,在面临多个辅助变量时,采用模型平均方法对超总体模型进行估计通常能够得到更贴近真实值的结果,这有助于综合多个模型的辅助效果,稳健且有效地提升抽样估计精度。
由于模型辅助估计方法结合了样本概率特征和模型信息,计算简单,且性质良好,长期以来受到学者们的广泛关注,并取得较为丰富的研究成果。就现有研究而言,主要可分为基于模型设置的研究[2—8]和结合具体问题的拓展研究[9—11]两个方面。虽然现有研究已关注了模型辅助抽样估计中模型形式的设置问题,并根据辅助变量类型及其与研究变量之间的关系特征,设定了不同的超总体模型用于辅助估计。但已有研究主要聚焦于如何构建合适的模型,而对于应该如何选择辅助变量的问题则关注较少。对这类问题的解决,最具代表性的就是模型平均方法。该方法主要通过设置合理的模型权重对多个可能的模型进行加权平均,能有效避免单一模型的选择偏差,最大限度地利用多个模型信息。
鉴于模型平均方法的估计优势及其理论日趋成熟,本文将在模型辅助抽样估计的框架下,引入模型平均方法,采用该方法对线性超总体模型进行估计,并以此修正基于设计的估计,试图提升模型辅助抽样估计的推断效率。同时,也将采用仿真模拟分析方法考察本文所提出的估计量的表现,并通过实际数据验证模型平均辅助抽样估计方法的估计效果。
1 模型辅助抽样估计及模型平均方法介绍
1.1 模型辅助抽样估计方法
模型辅助估计是指借助研究变量与辅助信息之间的相关关系构建相应的超总体模型,并以此作为辅助工具改进基于设计的估计方法。本文以模型辅助抽样估计方法中较为经典的GREG估计量为例进行介绍。

可以证明β̂是总体参数β的渐近设计无偏估计量,从而得到拟合值m̂(xi)=x'i β̂。那么可根据广义差分估计方法建立起HT估计量与辅助信息之间的联系,得到广义回归估计量:
1.2 模型平均方法
模型平均方法的思想是通过对多个模型的估计结果进行加权平均,进而得到平均估计或平均预测结果,其中模型权重的选择是决定模型平均估计或预测结果效果的重要因素。本文将介绍基于Mallows准则和信息准则两种权重选择方法的模型平均方法。


从以上过程可以看出,权重wr的选择是采用模型平均方法进行估计的核心问题。为此,Hansen(2007)[12]将Mallows 准则引入模型平均方法的研究中,提出用于模型平均的Mallows准则:

此外,基于AIC和BIC信息准则,Buckland等(1997)[13]提出了光滑AIC模型平均方法(S-AIC)和光滑BIC模型平均方法(S-BIC),具体的模型权重为:
其中,xICr=-2 log(Lr)+qr,Lr表示模型的似然函数,qr表示关于模型变量维度的惩罚项。当qr=2k时,该公式为AIC 表达式;当qr=klog(n)时,该公式为BIC 表达式。其中,k表示变量维度,n为样本个数。通过式(8)计算模型权重的模型平均方法称为S-AIC 和S-BIC 模型平均方法。
2 模型平均辅助抽样估计量构建及其统计性质
2.1 模型平均辅助抽样估计量构建
考虑多维辅助变量xi=(1 ,xi1,…,xiK)',i∈U,这里可以沿用式(1)建立研究变量和全部辅助变量之间的线性超总体模型,并运用模型平均法对式(1)进行估计。类似地,从K个潜在变量中任选k个辅助变量构成若干子模型,同样设置单一超总体模型为正态线性模型:

在运用模型平均辅助抽样估计时,需要事先确定式(10)中的模型权重wr的选择方法,这里主要采用基于Mallows 准则和基于信息准则的模型权重选择方法。其中,基于信息准则的权重计算方法与前文介绍较为一致,这里不再赘述。但基于Mallows准则的权重计算方法涉及基于总体数据的最小二乘估计,这里可以采用与式(2)类似的做法,根据HT估计进行加权最小二乘估计,进而得到基于样本数据的Mallows准则。
2.2 模型平均辅助抽样估计量的统计性质
考虑规模为N的有限总体递增序列UN,其中,U1⊂U2⊂…⊂UN⊂…。对于每个有限总体UN,可以按照抽样设计PN(sN)抽取一个大小为nN的样本sN,该样本的一阶包含概率和二阶包含概率分别为πi和πij。本文渐近性质的框架假定N是趋于无穷的,在此框架下,样本规模nN也是趋于无穷的。为了得到具备渐近设计无偏性和设计一致性的MA辅助估计量①在不同的模型权重计算方法下,MA辅助估计量可分为由Mallows准则计算权重的MMA估计量,以及由信息准则计算权重的S-AIC和S-BIC估计量,不失一般性,本文以MMA估计量为代表给出MA辅助估计量的渐近性质及相关证明。,这里给出如下假设:

其 中,假 设1 至 假 设5 是 借 鉴Robinson 和Särndal(1983)[5]关于GREG估计量性质研究的相关假定,类似假定也被用于非参数回归估计量的设定;假设6和假设7则是满足Mallows准则下的MA辅助估计渐近最优性的基本条件。
定理1:在假设1 至假设7 下,MA 辅助估计量满足渐近设计无偏性和设计一致性②由于篇幅限制,定理1及定理2的相关证明未在文中展示。。
性质1:渐近设计无偏性。
性质2:设计一致性。
定理2:给定假设1至假设7,有:
定理2说明MA辅助估计量的渐近均方误差和其方差具有渐近等价性,这表明MA辅助估计量的估计误差主要受抽样机制影响,而非模型拟合。
定理3:在假设1至假设7下,有:

3 数值模拟
3.1 模拟设计
本文的研究是建立在模型辅助抽样估计方法的基础上的,目的是解决在面临辅助变量选择时,怎样充分有效地利用辅助信息改进传统的GREG估计量。因此,接下来的模拟过程将以GREG估计量为基准估计量,对MA辅助抽样估计量展开对比分析。具体考察的估计量如表1所示。
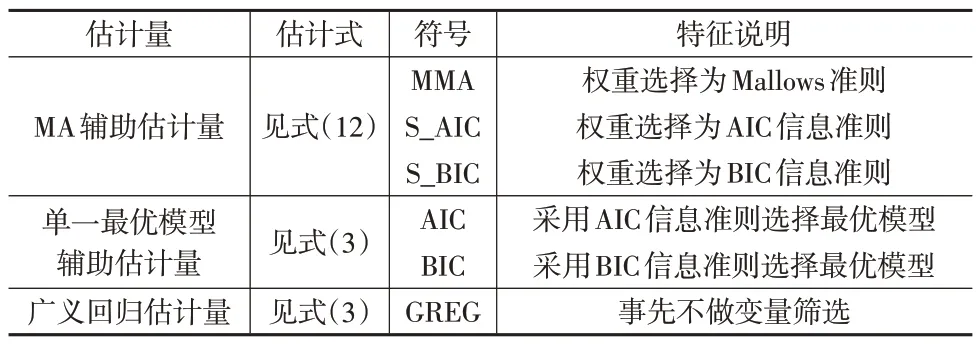
表1 所考察的抽样估计量
由于本文主要考察存在多个待选辅助变量时,如何进行辅助抽样估计的问题,这里构造一组包含多个辅助变量信息的总体,具体而言,将生成一组包含10个辅助变量和7个目标变量的研究总体[14],其中辅助变量服从以下分布:X1~U[0,1],X2~N(0,1),X3~Beta(3,1),X4~2×Gamma(3,2),X5~Bernoulli(0.7),其余5个辅助变量V1,V2,…,V5都服从均匀分布U[-1,1]。为了反映辅助变量对研究变量影响的差异,不妨设定G(X)=2X1+1.5X2+X3+0.5X4+0.005X5,表明X1至X5对研究变量的影响是依次递减的,且其他辅助变量与研究变量无关。进一步根据以下超总体回归模型生成模拟中用到的总体目标函数:

本文关于模型平均辅助估计量的研究是在超总体模型为线性模型的假定下展开的,因此在具有不同线性程度的总体下比较各估计量的估计效果很有必要。以上设置的7个回归函数分别反映了不同的线性程度,总体上可以认为从Y1至Y7回归函数具有的线性程度越来越低。
另外,以上7个总体目标函数的生成均基于G(X),表明所生成的研究变量仅和辅助变量X1,X2,…,X5存在相关关系,且这5 个变量的系数值依次递减,即和研究变量的相关性依次减弱。为分析模型平均辅助抽样估计方法在给定不同辅助变量时的估计效果,以下数值模拟过程将分别引入表2中的四组辅助变量进行分析。由表2可知,所引入的四组辅助变量分别表示变量选择完全正确、变量选择正确但不完全、变量包含全部正确信息及一些无效信息、变量选择均为无效信息。

表2 辅助变量选择

①设置不同样本数仅用于验证估计量的渐近性质,样本数本身不具有参考价值,实际抽样环节可根据具体情形而定。以下的各项模拟和实际数据验证环节亦是如此。
其中,ty为模拟中研究变量的总体总值,sb是指第b次抽样的样本,MSE(t̂y,greg)是GREG 估计量的均方误差,MSE(t̂y,*)是所要研究对比的估计量的均方误差。因此相对偏差和相对效率越小表示估计量的估计效果越优,一般而言,相对效率值小于1则表明该估计量的估计误差低于GREG估计量。
3.2 模拟结果分析
3.2.1 相对偏差分析
在给定不同样本容量、不同辅助变量及不同抽样方式下,本文对各个估计量的相对偏差值进行了模拟分析①由于篇幅有限,这里并未展示RB值的具体估计结果。。为了直观展示各个估计量的相对偏差表现,表3给出了不同样本量下RB 值的相关统计量。由表3 的结果可知,给定样本量n=50,MMA估计量RB值的均值为3.7523,在所有估计量中最小,然后为S_AIC 和S_BIC 估计量;MMA 估计量RB 值的标准差为5.8077,在所有估计量中最小;MMA 估计量RB 值的最大值和最小值也在所有估计量中最小。在样本量为100和300时,以上结论仍然成立,并且随着样本量的增加,多数估计量RB值的相关统计量均有所减小,这表明当样本量增加时,各估计量的估计偏差将会降低,这与预期一致。以上结果说明本文提出的模型平均辅助抽样估计量整体偏差最低,其中,MMA 估计量最优,且相较于选择单一最优模型进行辅助估计的方法而言,模型平均方法的稳定性更高。
3.2.2 相对效率分析
本文进一步在不同情形下对比分析了各估计量的RE值。由简单随机抽样下的估计结果②由于篇幅有限,这里并未展示RE值的具体估计结果。可知:(1)与GREG估计量相比,引进模型平均方法的MA辅助估计量优势明显且稳健,其中,以MMA估计量的优势最为突出。由模拟结果可知,各类情形下的估计结果均表明MA辅助抽样估计量在多数情形下优于传统的GREG估计量,少数情形下也至少和GREG估计量一样好(0.95 ≤RE ≤1.05)。(2)即使事前通过信息准则选择最优模型进行辅助估计(AIC 和BIC 估计),其估计误差也大于基于模型平均的估计量。(3)对比不同辅助变量选择下的抽样估计结果,当选择全部辅助变量(all)和无效辅助变量(uncorr)两种情形时,MA辅助估计方法的估计效率明显优于选择部分相关变量(part)和全部相关变量(corr),其中,MMA辅助估计量的估计效率最高。这说明在辅助信息选择有误时,模型平均辅助抽样估计方法相较于传统的广义回归估计量具有明显优势。(4)在目标函数为线性函数的情形下,MA辅助估计量相对GREG估计量的优势不明显;在目标函数为非线性时,MA辅助估计量的估计优势略有提高,尤其是在选择全部辅助变量(all)和无效辅助变量(uncorr)时,RE 值更低。此外,通过对比不同样本量下的估计结果可知,随着样本量的增大(固定抽样方式、辅助变量选择和目标变量等不变),模型平均辅助抽样估计量相对于广义回归估计量的优势有所降低,这一结果与渐近理论吻合。
为了更加直观地比较与分析,本文对各个估计量的RE 值进行整合,给出了各个估计量RE 值的相关统计量,具体结果见表4。
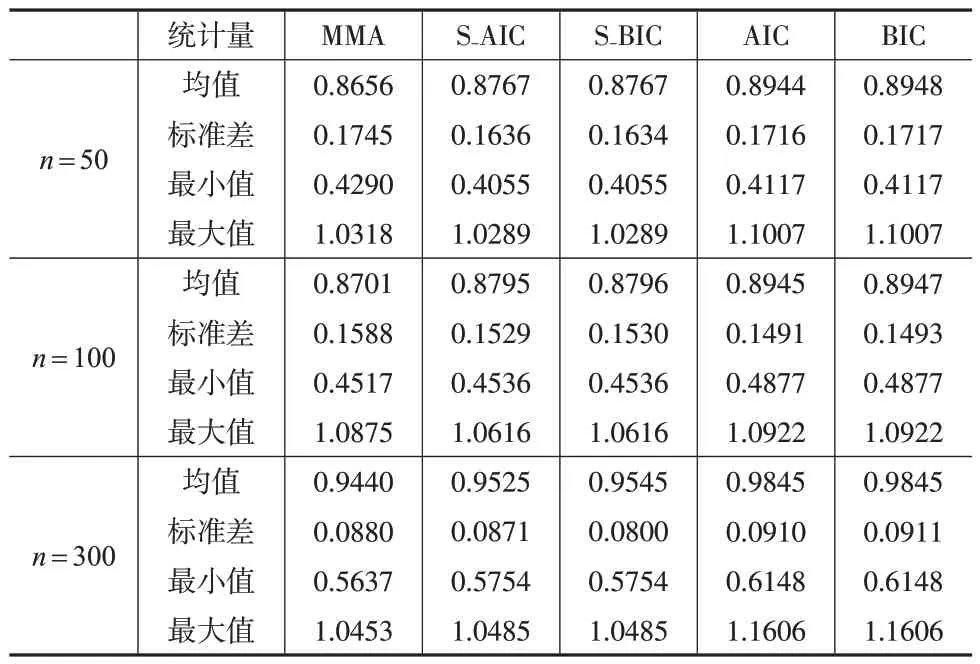
表4 RE值的相关统计量
由表4中的结果可知:(1)三个MA辅助抽样估计量的RE 值均值均小于1,表明在平均水平下MMA、S_AIC 和S_BIC三个估计量的估计误差小于GREG估计量。(2)三个MA 辅助估计量中,MMA 估计量的RE 均值低于其他两个估计量,表明其估计效果更优。(3)对比AIC估计量和BIC估计量可以发现,MMA 估计量的RE 均值更低,且标准差更小,说明MMA 估计量整体估计效率高于单一模型辅助估计量,且在抽样估计中表现得更加稳定。(4)随着样本量增加,各类估计量RE值的均值都有所增加,但RE值的标准差却有所下降,表明随着样本量增加,各类估计量的估计优势逐渐趋同且估计效果也更加稳定。这一结论说明在利用小样本对总体进行估计时,模型平均辅助估计量具有较大优势。
4 实际数据验证
4.1 数据来源及预处理
为进一步验证估计量t̂y,fma在实际应用中的效果,本文采用2018年中国家庭追踪调查(CFPS)家庭库中的部分数据,对模型平均辅助抽样估计量和广义回归估计量的估计效果进行对比分析。选取CFPS家庭库中的城镇调查对象作为研究总体,研究变量为调查对象的家庭总收入,并选择了食品支出、家庭藏书量等10 个变量作为辅助变量①所选辅助变量仅用于验证各估计量的估计效果差异,本文并不讨论其理论意义,在实际抽样估计中可根据具体问题和数据可得性来获取系列辅助变量。。在剔除缺失值和无效回答后得到5237个观测对象,将其作为实证分析的研究总体,通过不放回简单随机抽样(SI)和不放回分层随机抽样(STSI)两种方式来抽取样本,进行1000次重复抽样,每个样本的数量为500。为了更好地体现总体单位之间的差异性,分层抽样使用10个分层,其中,层与层之间的边界值由总体单元的辅助变量界定,本文采用辅助变量转移性支出的等间距十分位数确定。与前文的数值模型类似,下文的实证分析也将根据相关系数和相关性检验结果设置四组辅助变量选择情形。
4.2 结果分析
表5给出了各类估计量在实际应用中的效果对比。
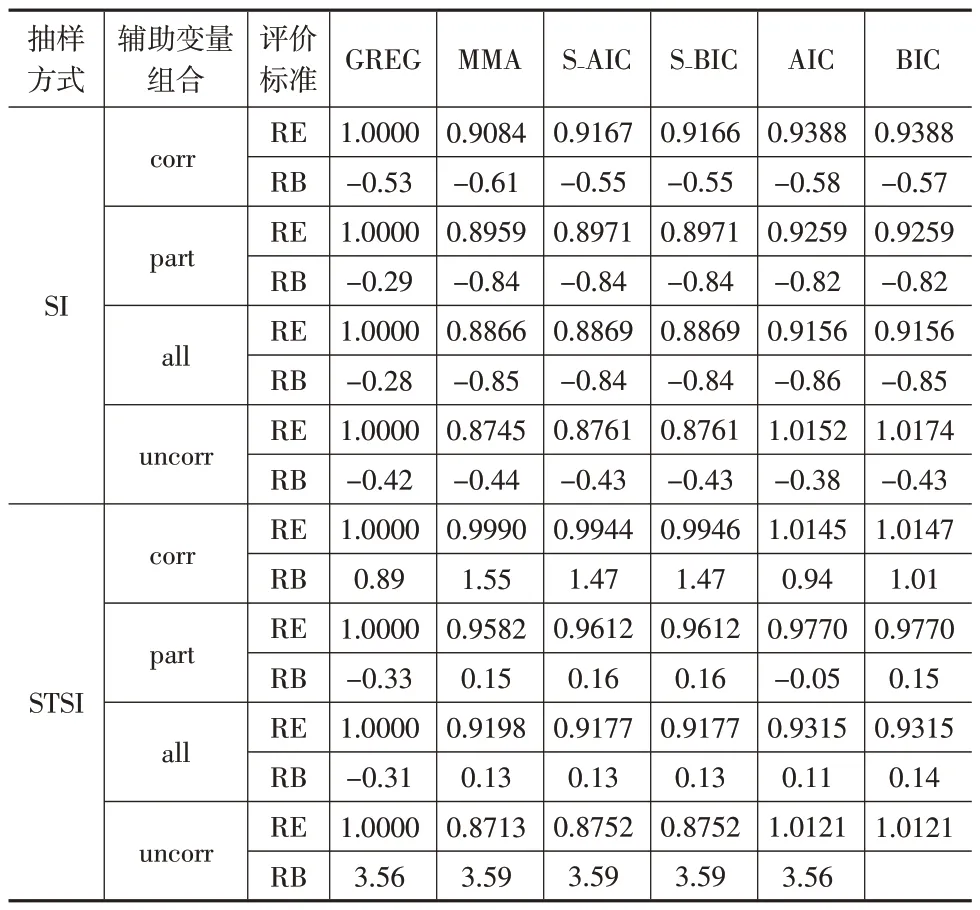
表5 基于CFPS城镇数据的估计结果
由表5 可知:(1)采用模型平均辅助抽样估计方法的估计结果明显优于广义回归估计方法,其中,MMA辅助估计量的估计结果最优。在各种情形下,MMA 辅助估计量以及S-AIC、S-BIC辅助估计量的相对效率值都明显小于1,这说明模型平均辅助抽样估计方法在实际应用中也优于广义回归估计量。(2)AIC、BIC 估计量表示采用AIC、BIC等信息准则对辅助变量进行筛选后再利用广义回归估计量进行估计的估计结果。表5结果显示,AIC、BIC 估计量明显不如模型平均辅助抽样估计量的估计效果,这说明即使事先对模型进行选择,仅采用最优模型辅助估计也不如模型平均辅助估计的效果,因为选择单一模型可能会导致模型选择偏差或有用辅助信息遗失,最终致使估计精度提高有限。(3)在不同变量组合下,当所选变量中包含无效信息时,模型平均方法下的抽样估计量对于广义回归估计量的相对优势更加明显,这证实了在模型不确定情形下采用模型平均辅助抽样估计量的必要性。
5 结束语
本文在传统模型辅助估计方法框架下,针对模型选择的不确定性问题,将模型平均思想引入广义回归估计的框架中,构造了一类模型平均辅助抽样估计量,并进一步通过数值模拟和实证分析验证了所提出的估计量的估计效果。结果表明,采用MA辅助估计量进行估计的结果明显优于传统的模型辅助估计方法,能够避免模型选择偏差,充分利用获得的辅助信息,显著且稳健地提高抽样估计效率。模型平均辅助估计突破了传统单一模型辅助估计的限制,可以在一项抽样估计中引入多样化的辅助信息和模型结构,未来仍具有较为广阔的研究空间。
