基于GA-BP的古代玻璃类别预测与风化程度测定模型研究

曹宇轩,隋国荣

(上海理工大学光电信息与计算机工程学院,上海 200093)

0 引言(Introduction)

研究并确定文物成分一直是考古和文化遗产领域的难题,在文物的挖掘过程,由于缺乏相关的信息,以及受环境和人为操作等多方面因素的影响,不可避免地出现了文物损坏现象,导致古代文物携带的历史信息缺失。因此,通过现有文物,快速、准确地识别文物的某些特定参数,对考古和文物保护工作具有重要的价值。

玻璃的生产历史悠久,最早可追溯至公元前2600年左右的美索不达米亚文明,是人类历史中重要的历史文物。玻璃最常见的风化机理是周围环境的水分子与玻璃网结构键之间的反应。这一现象使暴露在自然环境中的古代玻璃的光学、化学性质产生不可逆的变化[1]。宋代酱釉器及登封南洼遗址出土的白色项链等玻璃质的文化财产都受到严重的风化影响[2-3]。因此,古代玻璃的风化,不仅影响人类对古代文明的研究,还侵害了人类的文明财产。现阶段,保护古代玻璃方法亟待创新,目前尚未提出一种能对古代玻璃风化水平进行定量分析的模型。为此,本文根据古代玻璃的特点,建立一种全新的模型,首先使用GA-BP神经网络对玻璃样品的类别实现较高准确率的分类,其次利用主成分分析降维法对高维数据进行降维,最后结合熵权法实现对不同玻璃样本风化指数的数值评价。

1 原理与方法(Principles and methods)

1.1 遗传算法结合BP神经网络(GA-BP)预测玻璃类型

由于玻璃类型与其成分间存在的关系不是简单的线性关系,因此考虑使用BP神经网络处理该非线性问题。BP神经网络的每一层都由许多的神经细胞组成。每层神经元接收来自前一层的输入,并通过传递函数将计算结果输出到下一层[4]。

假设输入层的节点数为m,输入层的输入为,隐藏层的节点数为n,输出层的节点数为q,输入层到隐藏层的权重为ωij,隐藏层到输出层的权重为ωj k,输入层到隐藏层的偏移量为a j,隐藏层到输出层的偏移量为b k,学习速率为η,激励函数为g(x)。那么,隐藏层H j的输出如下:

计算误差如下:

其中,i=1,2,…,m,j=1,2,…,n,k=1,2,…,q;i为输入层编号,m为输入层节点数,j为隐藏层编号,n为隐藏层节点数,k为输出层编号,q为输出层节点数,Y k为期望输出。神经网络示意结构如图1所示。

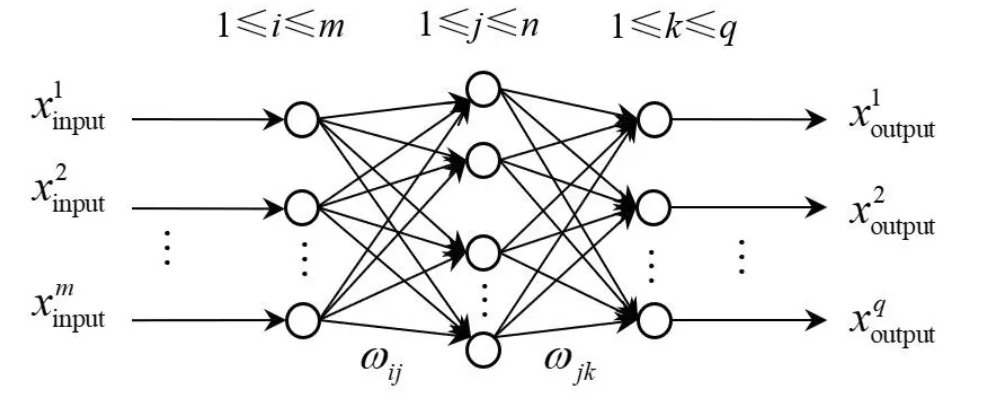
图1 神经网络示意结构Fig.1 Structure schematic diagram of neural net work

如果输出层的期望输出值与实际输出值的误差大于预定值,则误差将反向传播。通过调整各层的连接权重和阈值,逐渐减小计算值与实际值之间的误差,直到误差达到预定要求[5]。但是,BP神经网络在训练过程容易陷入局部最小值,为克服这一缺陷,本文使用遗传算法优化BP神经网络[6]。

遗传算法是通过模仿遗传进化和生物的自然选择而发展起来的一种优化算法,其主要特征是基于种群的进化,适者生存,具有定向性和随机性,并且不依赖梯度信息,它包括编码、选择、交叉、突变和解码操作5个过程。

本模型利用遗传算法的全局寻优搜索功能获得每一次的最优种群,接着利用BP神经网络的局部寻优特征,反向寻得最优值[7]。

本文选取三层结构的神经网络,包括输入层、隐藏层和输出层,每层包含一定数量的神经元。对于基于GA-BP神经网络的玻璃类别预测模型,影响因素包含14种化学成分的含量。因此,设置输入层节点数为14,即m=14,样本数量为69。因为仅研究玻璃的类型,所以输出层节点数为1,即q=1。本模型将预测输出与期望输出的平均误差值Error作为个体的适应度函数,其定义如公式(4)所示:

其中,xtrain为样本的实际玻璃类别,t为样本编号。Error越大,该个体的适应度值越大,则该个体越容易在种群迭代的过程中被淘汰。通过遗传算法不断迭代,最终找到最优的隐藏层数量。

从图2可以看到,在种群迭代次数为41时,网络迎来最优适应度,其隐藏层的数量为8,即j=8。

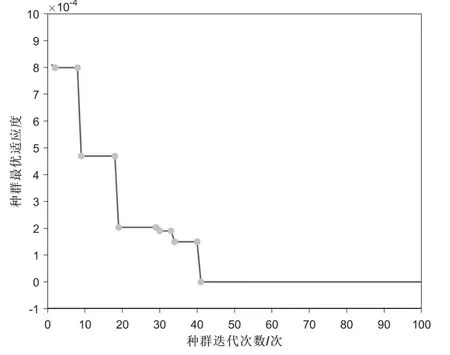
图2 种群迭代次数与最优适应度关系Fig.2 The relationship bet ween the population generation number and optimal fitness

本文所提分类模型首先将样本数据随机分散,然后选择50个样本作为训练样本,10个样本作为测试样本训练神经网络,9个样本作为验证集,其中69个样本分为高钾玻璃和铅钡玻璃。在实验过程中通过调整特征向量、激活函数、训练算法、学习速度等,获得最佳的实验结果,达到最高的准确率。本文使用8个隐藏层构建神经网络模型。隐藏神经元传输函数选择logsig函数,输出层传输函数选择tansig函数。训练神经网络的算法使用trainlm算法。学习速度设置为0.1。训练目标误差设置为0.000 1。最终通过Matlab R2020a软件搭建GA-BP神经网络仿真平台,并得到以下实验结果。

从图3可以看出,网络训练迭代至第7代时,训练集误差满足目标误差条件,此时验证集均方误差最小,仅为0.000 521 22,同时该网络收敛速度快,不存在锯齿现象。

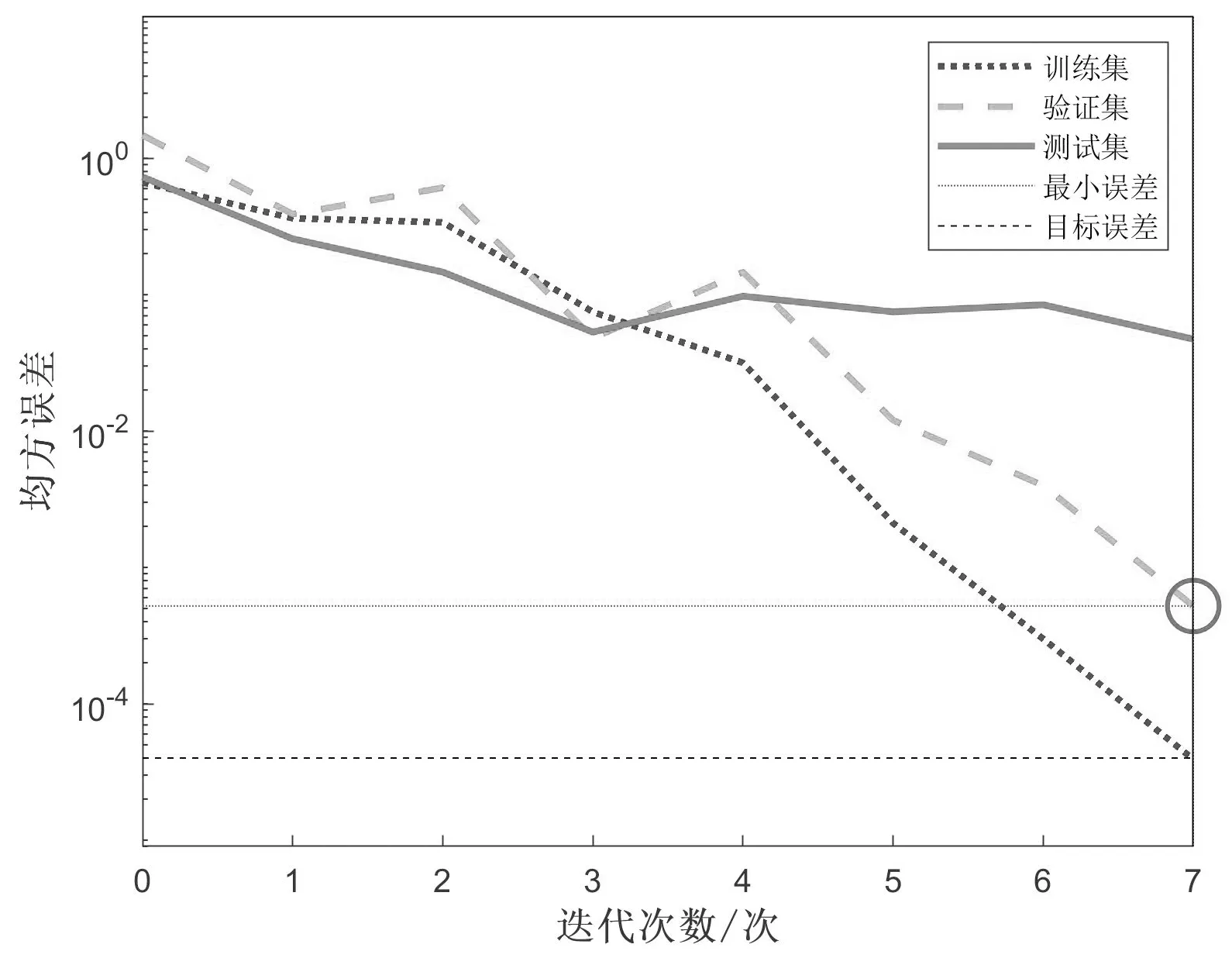
图3 网络训练次数与均方误差Fig.3 Net work training times and mean square error

为衡量GA-BP神经网络在各个数据集中期望输出与实际输出的偏差,本文引入拟合优度R的概念,其定义如公式(5)所示。拟合优度R是指回归直线对期望输出的拟合程度,其最大值为1且其值越接近1,说明回归直线对期望输出的拟合程度越好;反之,说明回归直线对期望输出的拟合程度越差,即训练的GA-BP神经网络质量越差。

通过图4可以看出,网络训练集、测试集、验证集以及总数据集拟合优度均高于97.8%,证明该神经网络的优越性。

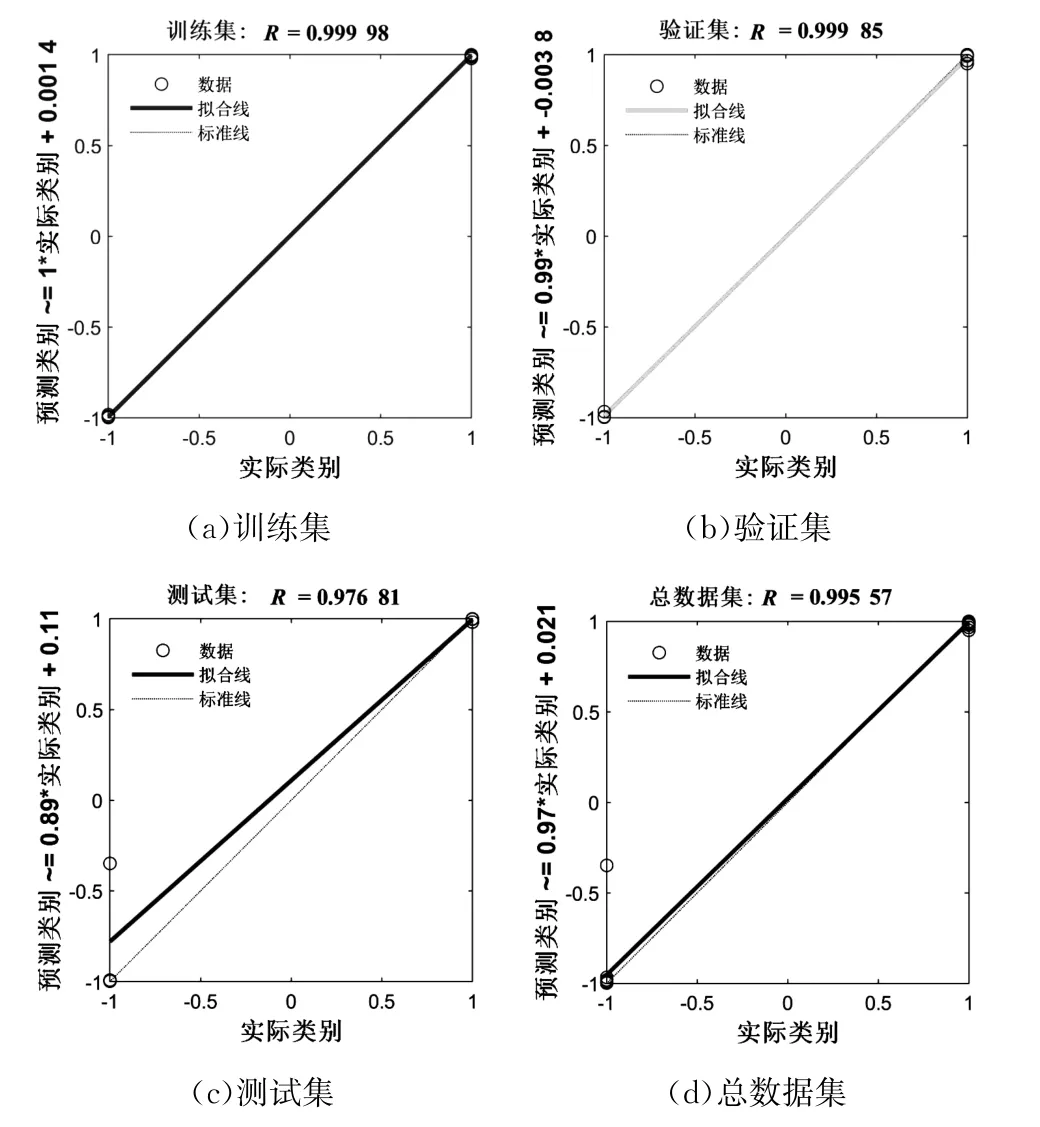
图4 各数据集拟合优度Fig.4 Goodness fit of every data set

图3和图4证明该网络能够成功区分训练集玻璃的类别,并具有较高的准确率。

1.2 主成分分析降维

主成分分析(PCA),被视为经典数据降维方法,在模式识别和计算机视觉领域得到广泛的应用。PCA是一种多变量统

计技术,根据捕获的所有信息,可将数据量减少至较小的数量,并提取特征信息[8];其基本思想是重新组合原始相关索引X1,X2,…,X k(该矩阵已进行数据中心化处理),形成少量不相关的综合指标。综合指标应最大限度地反映原有变量所代表的信息,并能保证新指标相互独立,从而尽可能多地保留原始变量中所包含的信息,以达到数据降维和稀释数据信息的目的[9]。如果F1,F2,…,F n用于表示原始变量的n个主成分,即可得到:

随后,本文将分别计算铅钡玻璃和高钾玻璃中各种化学成分的贡献率,并进行降序排序,同时依次算出每种化学成分对主成分的累计贡献率。为尽可能对数据进行降维以及保存数据的信息量,本文将累计贡献率的最低标准划分为90%。

由图5可知,对于铅钡玻璃而言,其14种化学成分降维至9个主成分即满足累计贡献率达到90%的条件。对于高钾玻璃而言,仅需要6个主成分即可满足条件。

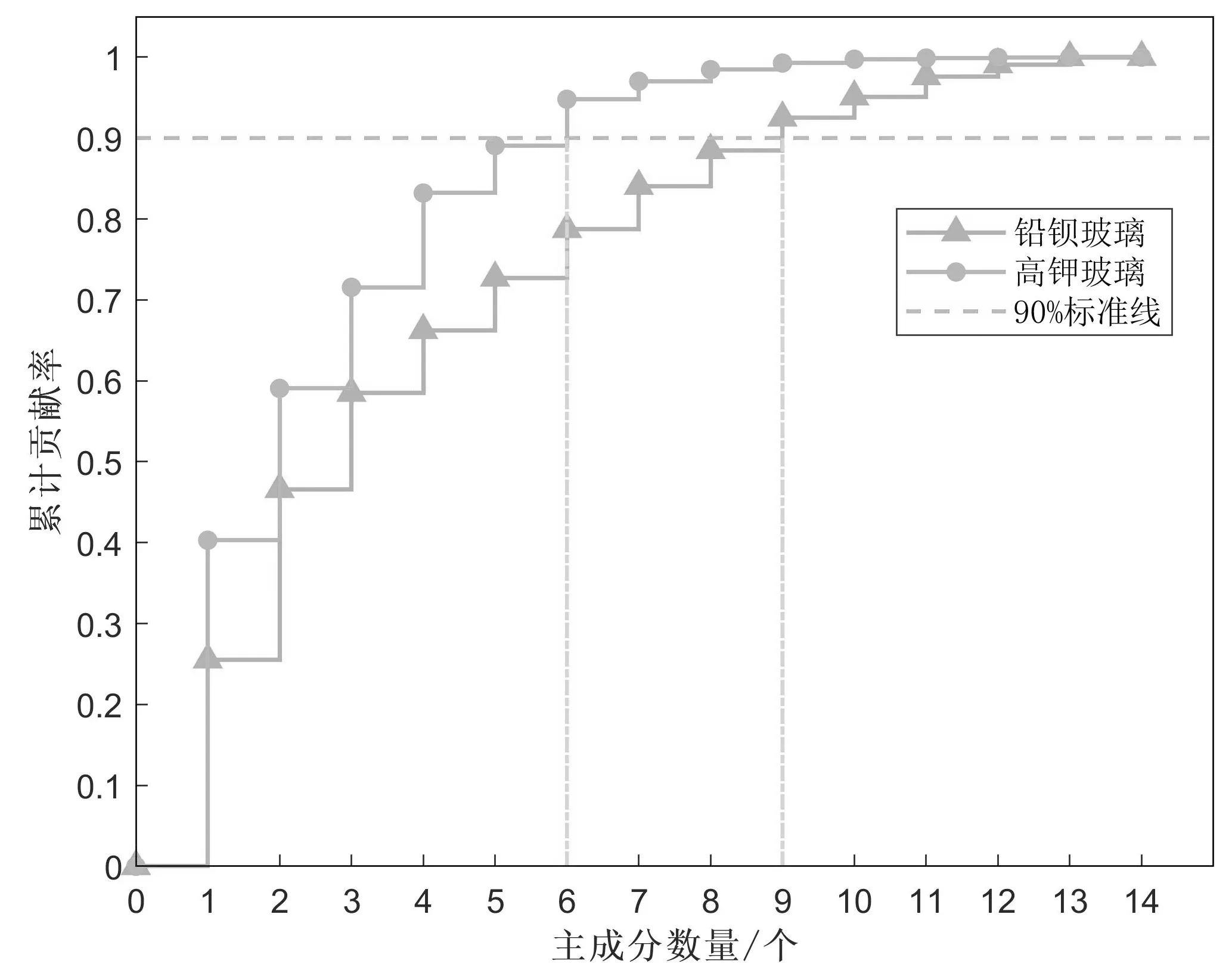
图5 累计贡献率阶梯图Fig.5 Ladder diagram of cumulative contribution rate

1.3 熵权法确定风化程度

决策者的主观考虑会造成指数权重的偏差,为避免这类干扰,产生符合事实的结果,使用基于指标固有信息的客观权重法确定权重[10],因此选择熵权法(EWM)模型,其模型实现过程如下。

步骤1:将经过PCA降维后的主成分F1,F2,…,F n正向化为,对于正向指标:

对于负向指标:

假设各指标数据标准化后为Y1,Y2,…,Y n。

步骤2:将Y ij进行数据归一化处理,处理过程如公式(9)所示:

其中,m为样本数量。

步骤3:计算所有样本指标的熵值E,范围在0～1,其计算公式如下:

步骤4:具有较小熵值的指标表示大量信息,即指标具有更高的重要性且应当具有更高的权重。因此,使用公式(11)计算熵权重ωe:

步骤5:利用熵权重ωe计算得分,将其转化为百分制,并定义其为未风化程度指数Score。Score计算公式如下:

其中,n为主成分数量。

2 模型实验(Model experiments)

根据模型计算,分别得到不同材质玻璃的不同样本的未风化程度指数。

对高钾玻璃而言,在现有的玻璃样品库中,试验发现风化玻璃与未风化玻璃的未风化程度指数分界点,所有风化玻璃的未风化程度指数均小于20,并且15号样本的风化最严重,仅为9.709,其结果如图6所示。

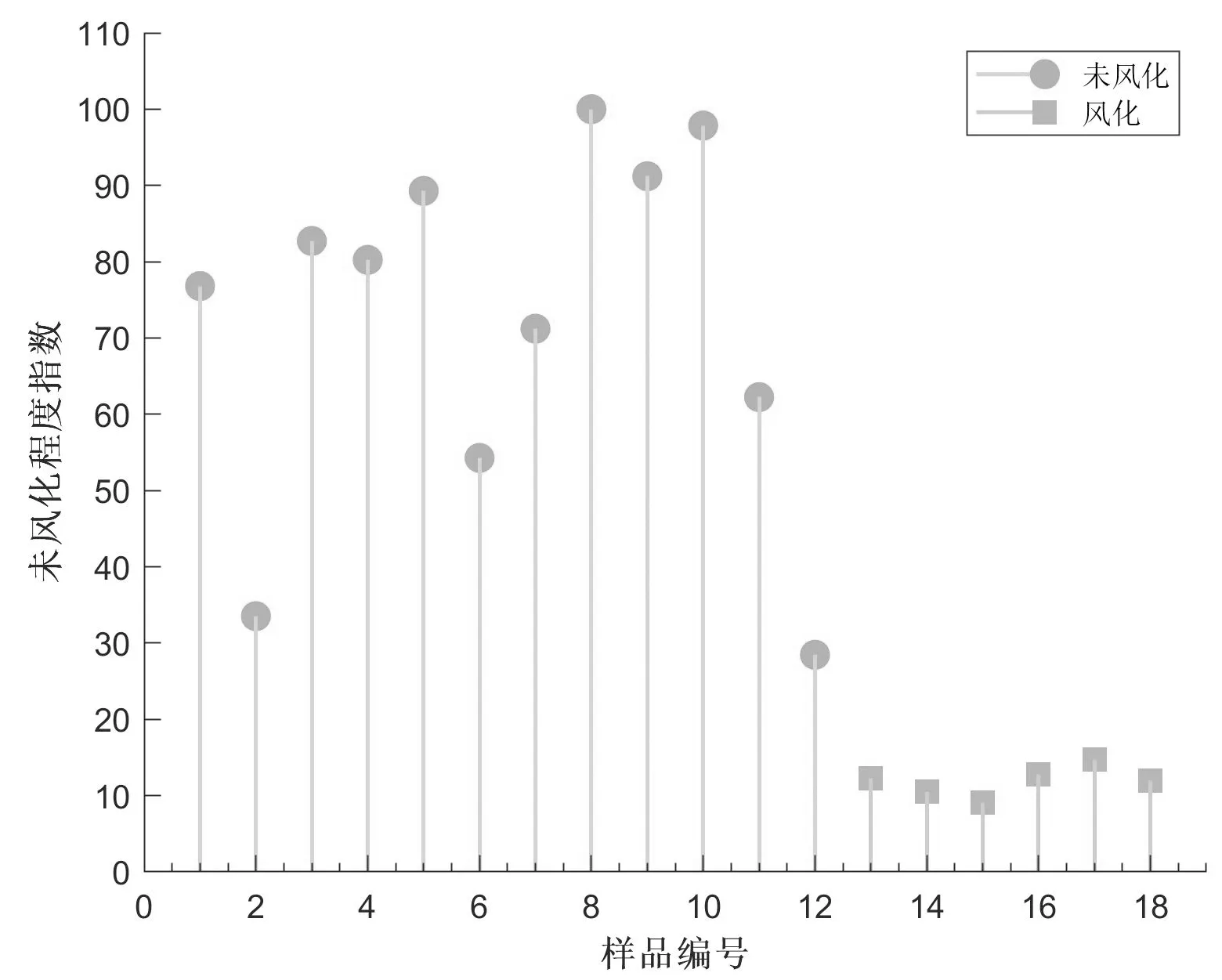
图6 高钾玻璃未风化程度Fig.6 Unweathering degree of high potassium glass

对于铅钡玻璃而言,试验也能观察得到风化玻璃与未风化玻璃的未风化程度指数分界点在53,并且第37号样本的风化程度最严重,未风化程度指数仅为21.404,其结果如图7所示。

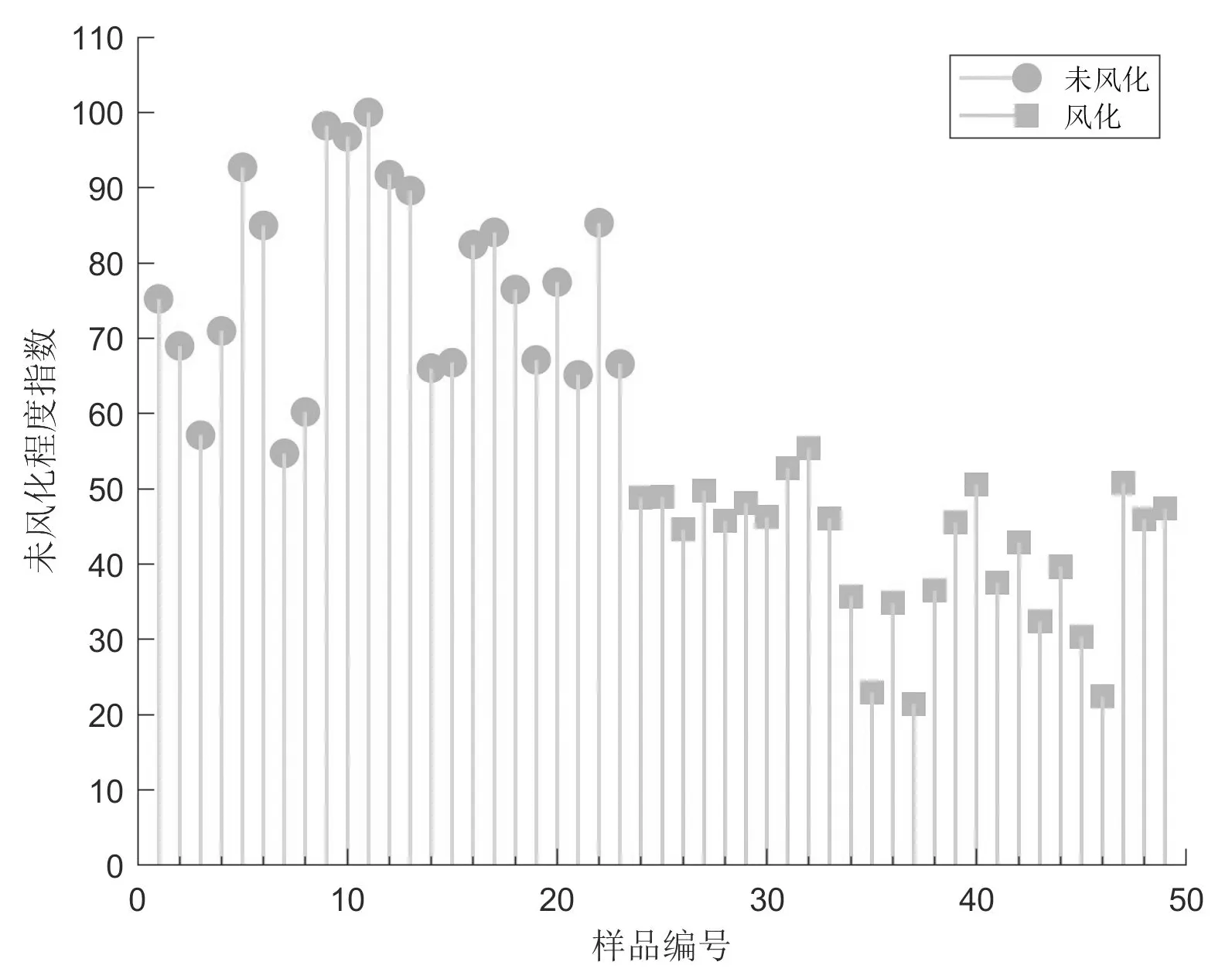
图7 铅钡玻璃未风化程度Fig.7 Unweathering degree of lead barium glass

由图7中的结果可知,随着玻璃测量样本数量的不断增加,模型越精确。

3 结论(Conclusion)

本文建立GA-BP优化模型,通过选择合适的隐藏层,极大程度地降低神经网络的预测误差,从而可以根据14种化学物质的含量精确预测样本的玻璃类型。同时,利用PCA降维,配合熵权法,对每个样本的风化程度进行评分,并进一步划分高风化程度分数线。因此,对于挖掘出土的古代文物,可利用无损检测手段在第一时间分析其化学成分,并针对风化严重的区域做出针对性的保护措施。

本模型在大样本数量的环境下,不仅可以评估当前环境是否会进一步加剧文物的风化程度,也能通过未风化程度指数,帮助考古学家在挖掘文物的过程中提前制定技术路线和设置技术参数。此外,本模型应用于在建筑行业时,配合强化风化条件,可以得到一个警戒风化分数并定期对玻璃的风化程度进行量化比较,确保建造结构的安全性。