联合神经与遗传算法的发动机进气管参数优化
2023-07-12张袁元韦思航
张袁元,陈 丹,韦思航
(南京工程学院 汽车与轨道交通学院,南京 211167)
0 引言
发动机进气系统用来控制和调整进气流量和速度,使气缸中充入新鲜工质并具有一定气流运动,从而促进燃烧。影响进气质量流量的重要参数除了进气管几何形状外,也受到活塞下行和进排气门运动中产生的压力波动干扰。因此,合理的进气管和气体动态效应的有效结合,可以有效提高发动机充气效率,改善发动机的性能[1]。
Hadjkacem等[2]基于进气系统的波动动力学,研究了进气室长度对发动机性能的影响,结合实验数据确定了转速对应的最佳进气长度。李玉龙等[3]给出了气动发动机进排气管路系统设计的一般要求,从而确保了对进气量的精准控制,降低了气体损耗,使两级式气动发动机能够稳定运转。杨帅等[4]通过提高进气增压压力、合理优化进气管几何结构,减少柴油机在进气过程中出现的进气分配不均匀现象。文献表明,进气管结构参数改变对充气效率的改善带来有益效果,从而提升发动机性能。
程雪利等[5]以增程式发动机为研究对象,利用实验设计技术对气门升程曲线、进气歧管及进气道结构进行优化研究,提高了低速段扭矩和平均滚流。Bhatt等[6]和Herawan等[7]利用神经网络和遗传算法,确定配气相位对发动机性能和燃油经济性的影响并进行优化;Ahmed等[8]提出了一种结合人工神经网络的发动机排气能量回收方法;Syed等[9]研究了建立高效人工神经网络(ANN)模型的可行性,将其作为进一步研究双燃料柴油机的工具;Lu等[10]提出了基于最优算法对发动机电磁阀控制参数进行优化。张鹏等[11]研究了实验设计(design of experiment,DOE)和人工神经网络构建排气温度预测模型。DOE技术、神经网络算法、遗传算法、响应面等智能优化算法在发动机领域的运用,为发动机系统参数优化提供了新的途径。但采用多种方法集成对进气管结构进行参数优化鲜有研究。
本文搭建发动机一维系统仿真模型,通过外特性实验曲线修正,分析进气管结构参数对发动机的性能影响,集成神经网络和遗传算法,对进气管参数进行设计,以获得最优发动机性能,为可变进气管的结构优化设计提供理论依据和方向。
1 一维系统仿真模型的建立
1.1 发动机技术参数
高速汽油机为单缸四冲程,具体参数如表1所示,适用于摩托车、发电机、ATV等。

表1 发动机技术参数
1.2 发动机系统仿真模型构建
发动机工作过程复杂,涉及多学科耦合,工作时需要考虑管道壁面以及壁面与外界环境之间的热传导、热辐射、燃烧放热过程、放热速率、管道内摩擦、气缸内摩擦、爆震、熵变等一系列因素。
发动机系统仿真模型包括进气、排气、气缸、曲轴箱、空气滤清器、喷油器等模块。进排气管道气流简化为一维非定常流动模型;管道摩擦损失、压力损失采用Chen-Flynn的关系式,即摩擦损失压力为活塞速度和峰值压力的函数[3-4];燃烧模型为点燃式湍流火焰燃烧模型,以准三维可预测模型SI-Turb为基础建立,满足在优化模拟过程中对进气管多参数调控要求;发动机摩擦损失采用Chen-Flynn总结出的经验公式进行计算,即EngFrictionCF模型;壁面热传导数学模型依据Colburn的相似理论;缸内热传导模型采用Woschni于1987年提出的半经验模型;喷油器使用InjAFSeqConn模型,其燃油喷射率(喷油脉宽)和空燃比通过实验获取。单缸发动机一维仿真模型基于GT-POWER搭建,如图1所示。
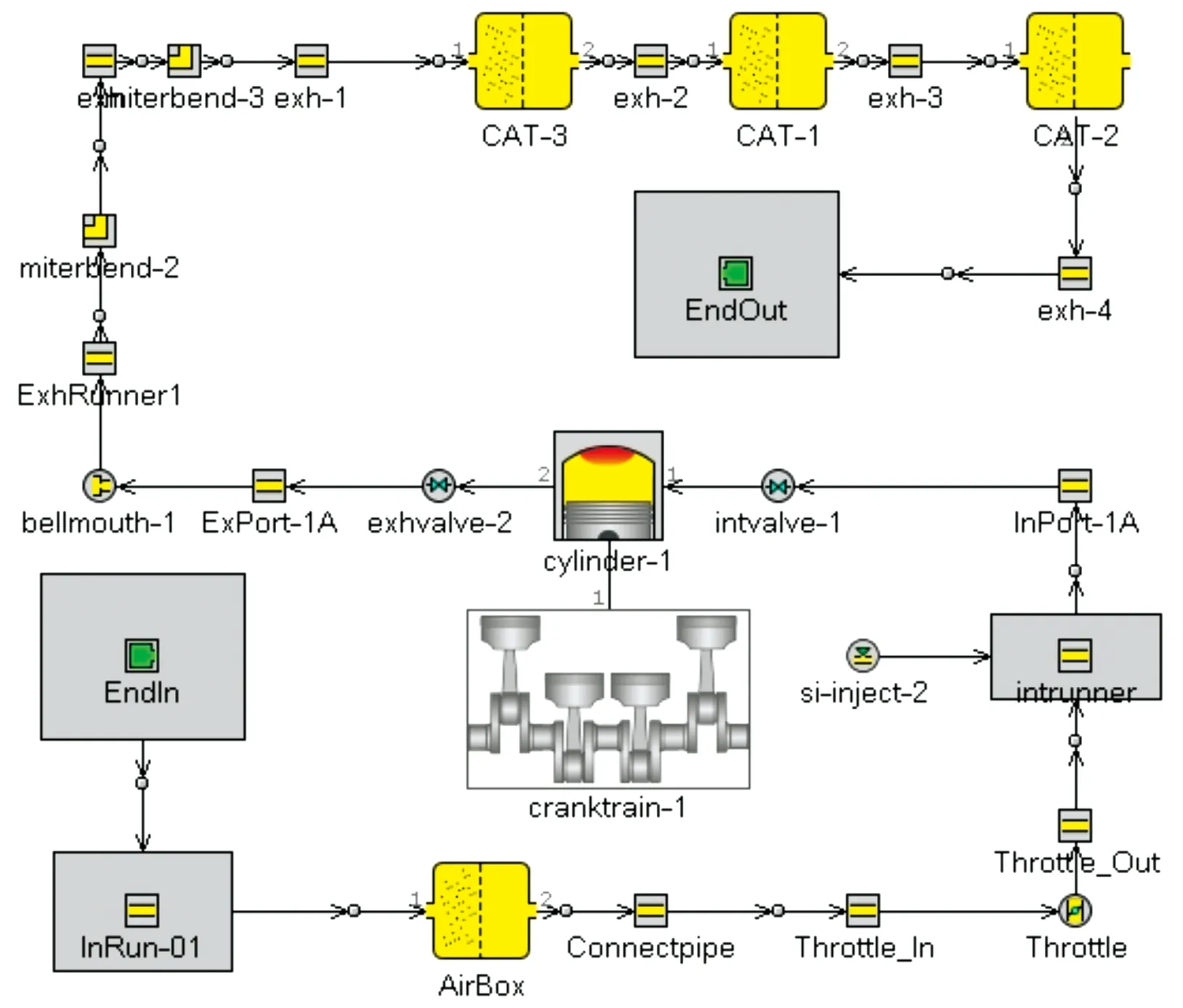
图1 发动机系统GT-Power仿真模型
1.3 系统仿真模型验证
选取发动机全负荷工况下,转速4 000~9 000 r/min的11个工况点(均匀间隔500 r/min),根据实验中进气温度、平均有效压力、点火提前角等数据校正模型后,通过仿真计算出发动机的外特性数据,并与台架实验外特性实验数据进行比较,如图2、图3所示。结果表明,功率和扭矩的性能特征最高误差不超过3%,燃油消耗率误差小于2%,证明系统模型可靠,能够表征和模拟发动机的工作过程,可将该模型作为发动机动力性能优化的基础。
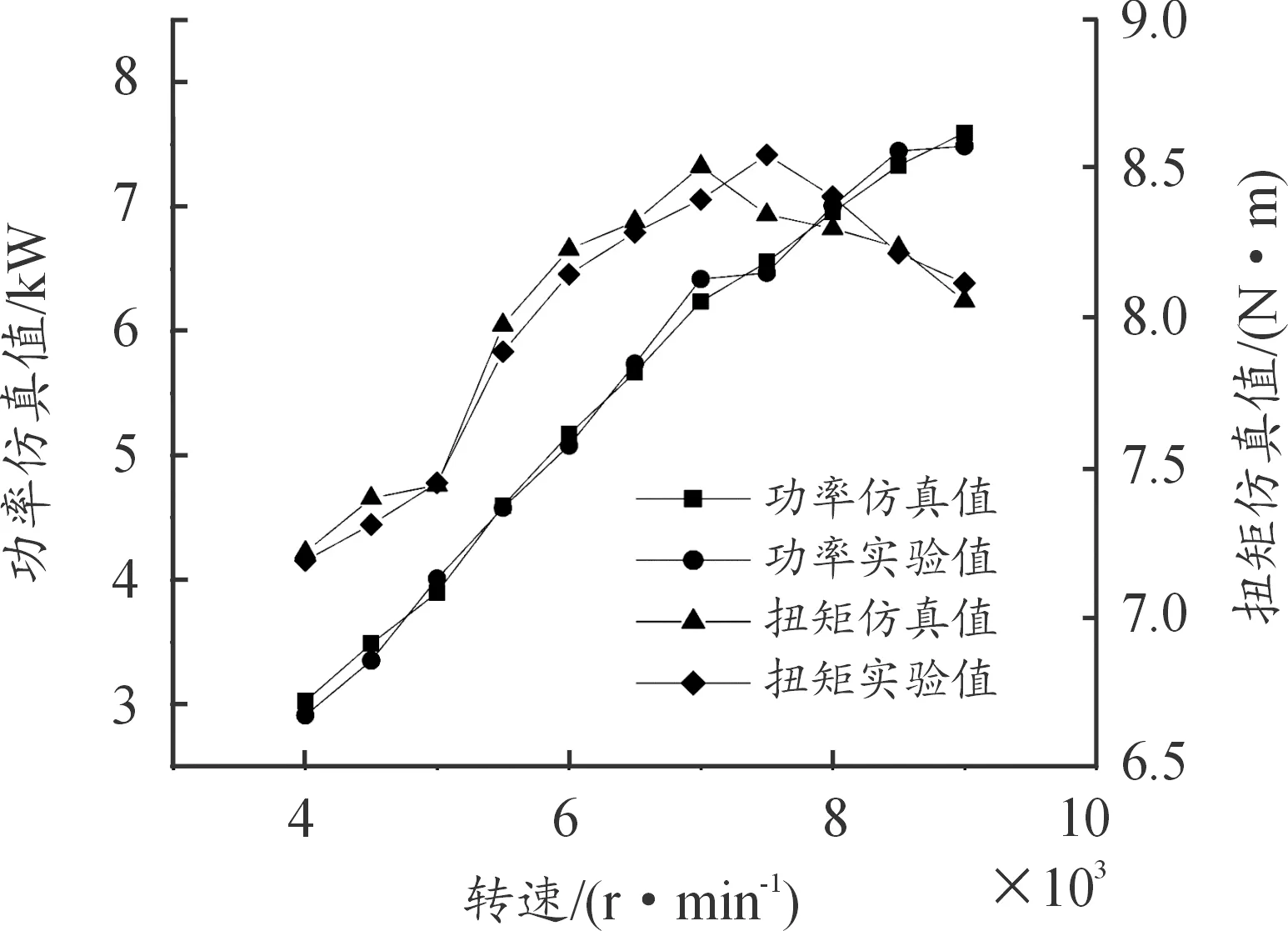
图2 发动机外特性功率扭矩对比
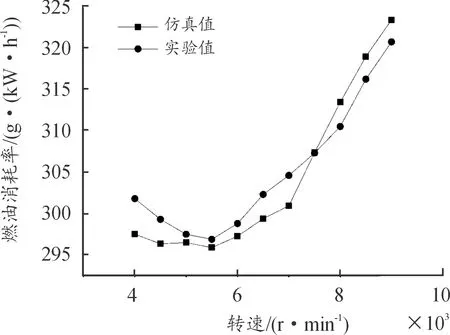
图3 发动机外特性油耗对比
2 进气管结构参数对发动机性能的影响分析
进气管结构参数包括长度、直径,在不同工况下,对发动机性能影响效果不同。
2.1 进气管长度对发动机性能的影响
进气系统长度包括进气管、空气滤清器以及其他进气附设结构,其长度引起的气流动态效应,会带来充气效率变化,主要包括惯性和波动效应。
q=0.5,1.5,2.5,…
(1)
式中:φse为进气行程曲轴转角,°;a为发动机进气管气流音速,m/s;n为发动机转速,r/min;Lgx为满足惯性效应建议进气系统长度;Lbd为满足波动效应建议进气系统长度。
根据惯性效应和动态效应公式(1),考虑进气管适用于发动机转速1 000~9 000 r/min,推荐最长和最短进气长度相差8倍,综合考虑空滤、气缸行程等尺寸,参考原进气管长度40 mm,结合进气管空间尺寸约束,系统模型中将进气管长度变化范围设置为40、80、150、320 mm,其他结构参数和配气相位不变。图4—7为不同长度的进气管对发动机性能影响。

图4 进气管长度变化对充气效率的影响
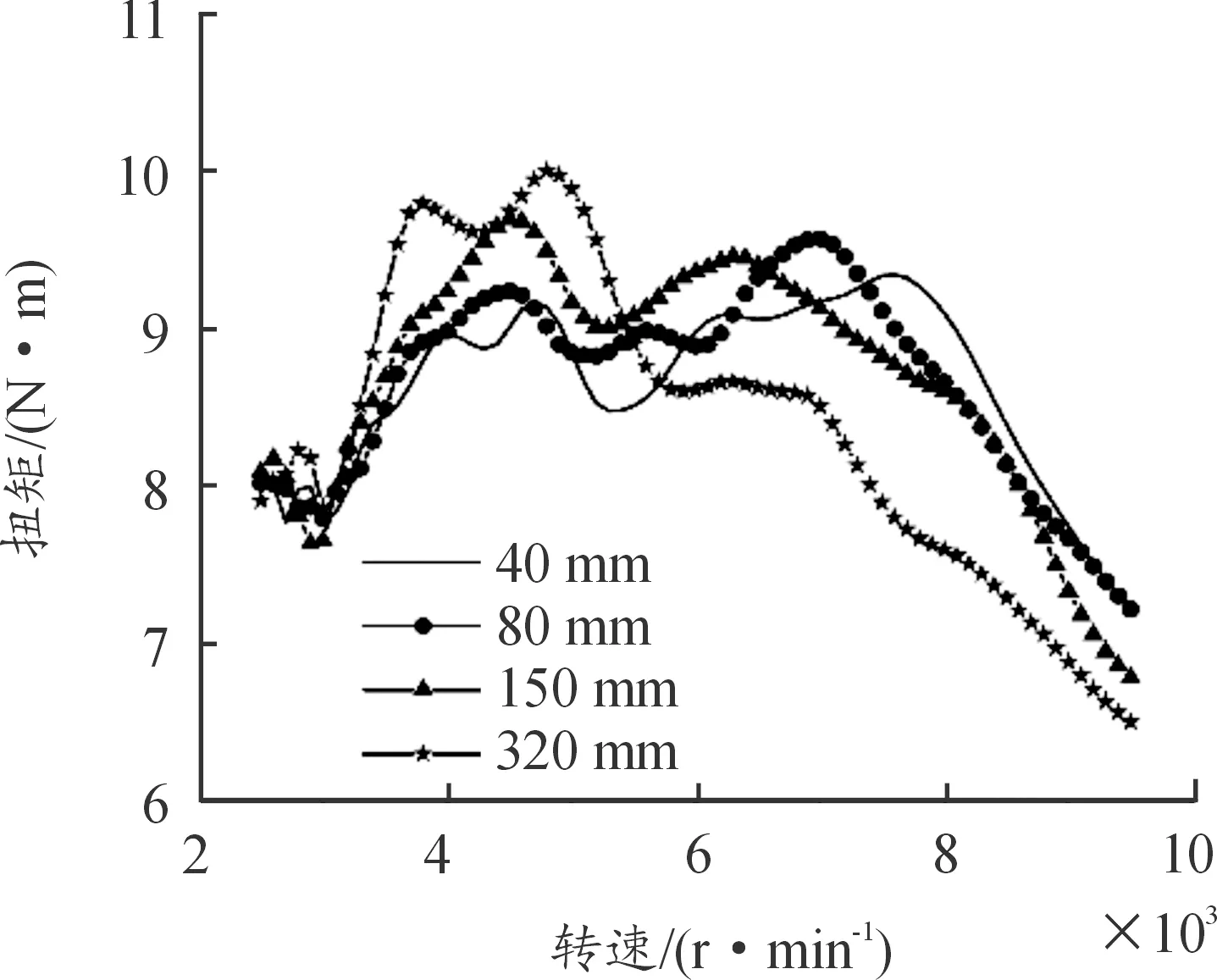
图5 进气管长度变化对扭矩的影响

图6 进气管长度变化对功率的影响
随进气管长度的增加,发动机充气效率峰值向低速区移动,整体呈现向左平移,发动机中速区充气效率改善作用明显;反观高速区域,进气管长度增加,进气摩擦损失增加,充气效率急剧下降(图4)。扭矩随着进气管长度的变化情况与充气效率趋势一致,即扭矩峰值随长度增加向低速移动(图5)。结合充气效率和扭矩影响,发动机功率呈现高速峰值下降,中低速增加,整体曲线随进气管长度增加其陡峭特征减小(图6)。比油耗随进气管长度增加在中低转速小幅下降、高速小幅增加,其长度变化对比油耗整体影响较小。总的来说,150 mm长度进气管兼顾的转速范围更大一些。
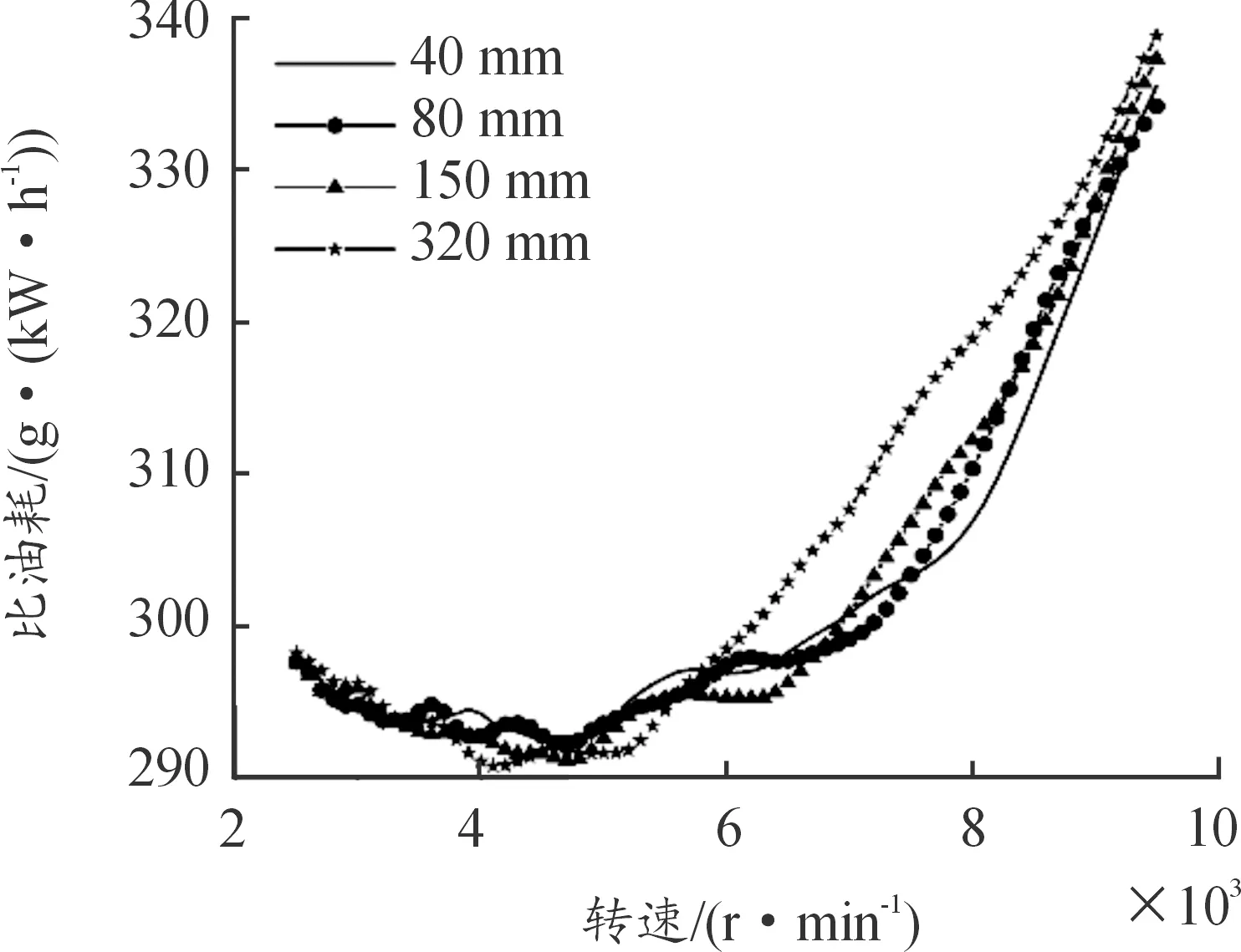
图7 进气管长度变化对比油耗的影响
2.2 进气管管径对发动机性能的影响
进气系统等效管径越大,摩擦损失越小,但气流波动幅度减小,进气谐振效果下降。因此,合理的进气管径可以促进进气波动效果,增加充气效率。Kastner给出了最小管径的经验估算公式(2):
(2)
式中:d为气缸管径;S为发动机冲程;n为发动机转速。
原机进气管管径26 mm(依据常用转速3 000~6 000 r/min设置),依据管径计算公式,管径设置范围约为22~33 mm,因此设置23、26(原机)、29和32 mm 4个定常参数,研究管径变化对发动机性能影响。其他结构参数和配气相位以原机的基本技术参数为准,图8—11为不同管径的进气管对发动机功率、扭矩、充气效率以及比油耗的影响。
进气管管径越小,发动机转速越高,进气气流流速和流动阻力越大,充气效率和进气质量流量越低(图8);扭矩影响与充气效率影响一致(图9)。因此在发动机高转速区间,可以采用更大管径的进气管。在发动机低转速区间,不同管径的进气管对动力性能参数的影响不显著,高转速时曲线随进气管管径增加其陡峭特征略有增加(图10)。增加进气管的管径对比油耗的影响较小(图11),然而减小管径会对提升高转速下的比油耗,降低经济性能。与原机管径为26 mm的进气管相比,采用32 mm管径的进气管在7 000、7 500、8 000、8 500和9 000 r/min时,功率和扭矩分别提升了4.6%、1.6%、0.5%、2.1%、6.5%。

图8 进气管管径变化对充气效率的影响
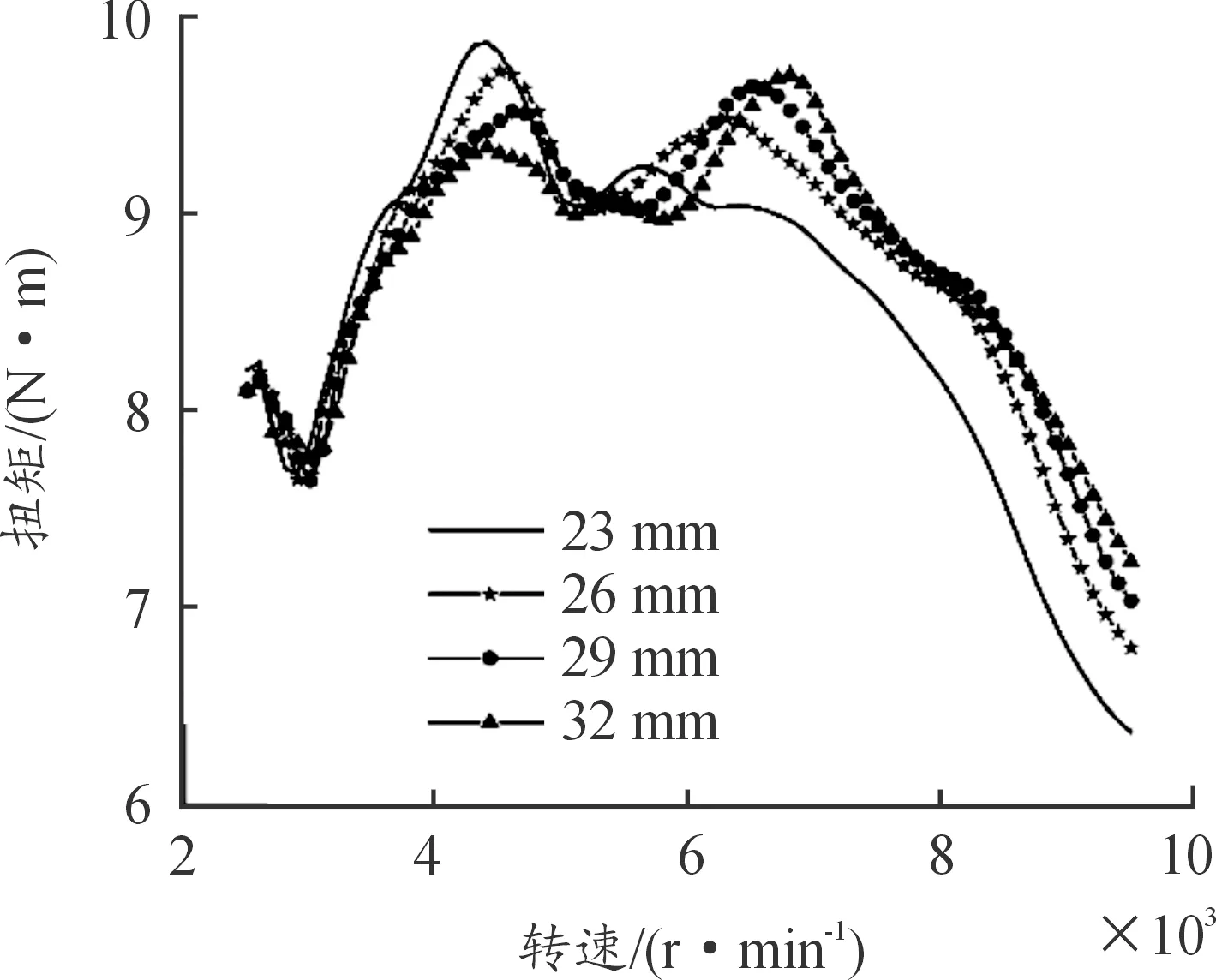
图9 进气管管径变化对扭矩的影响
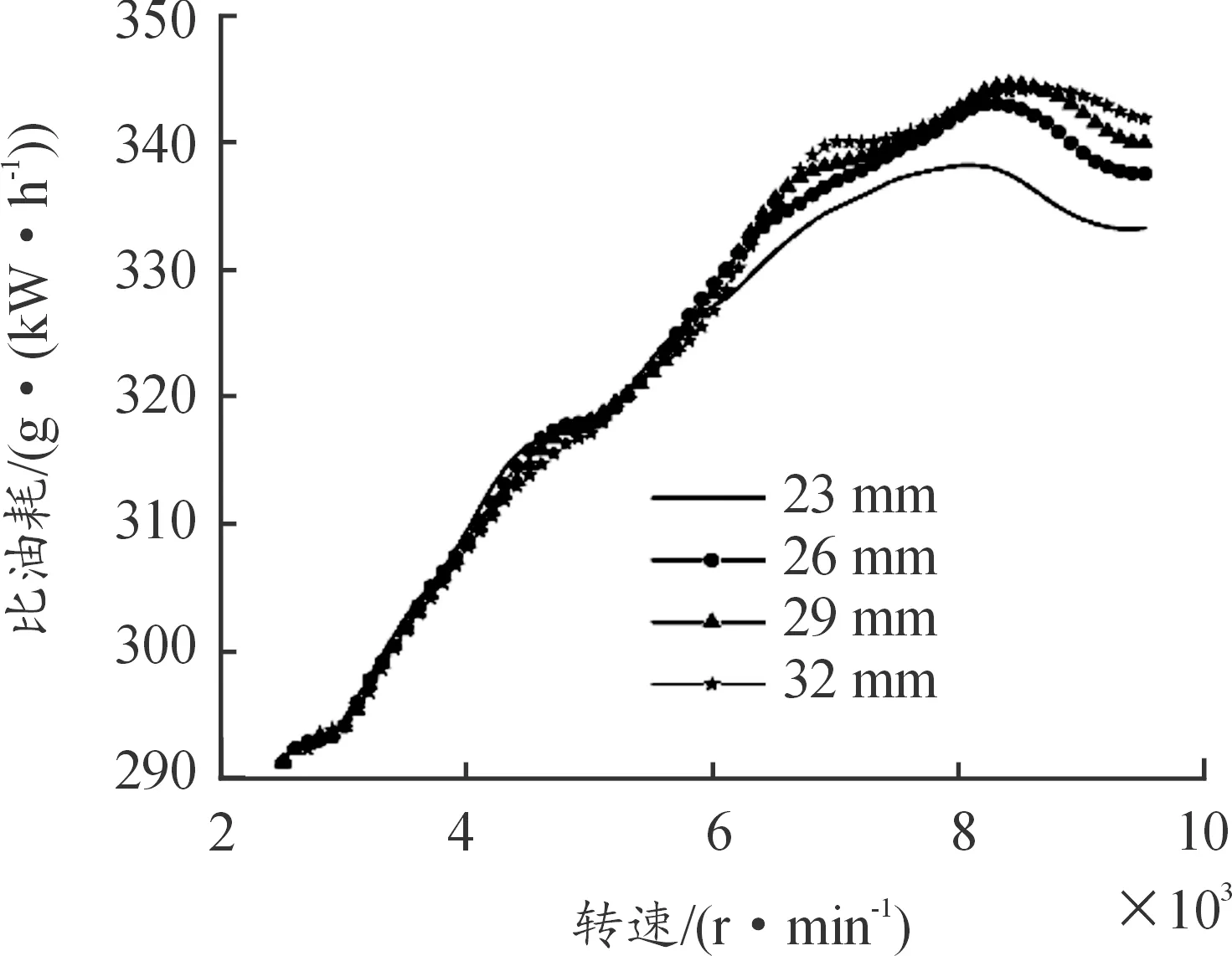
图10 进气管管径变化对功率的影响
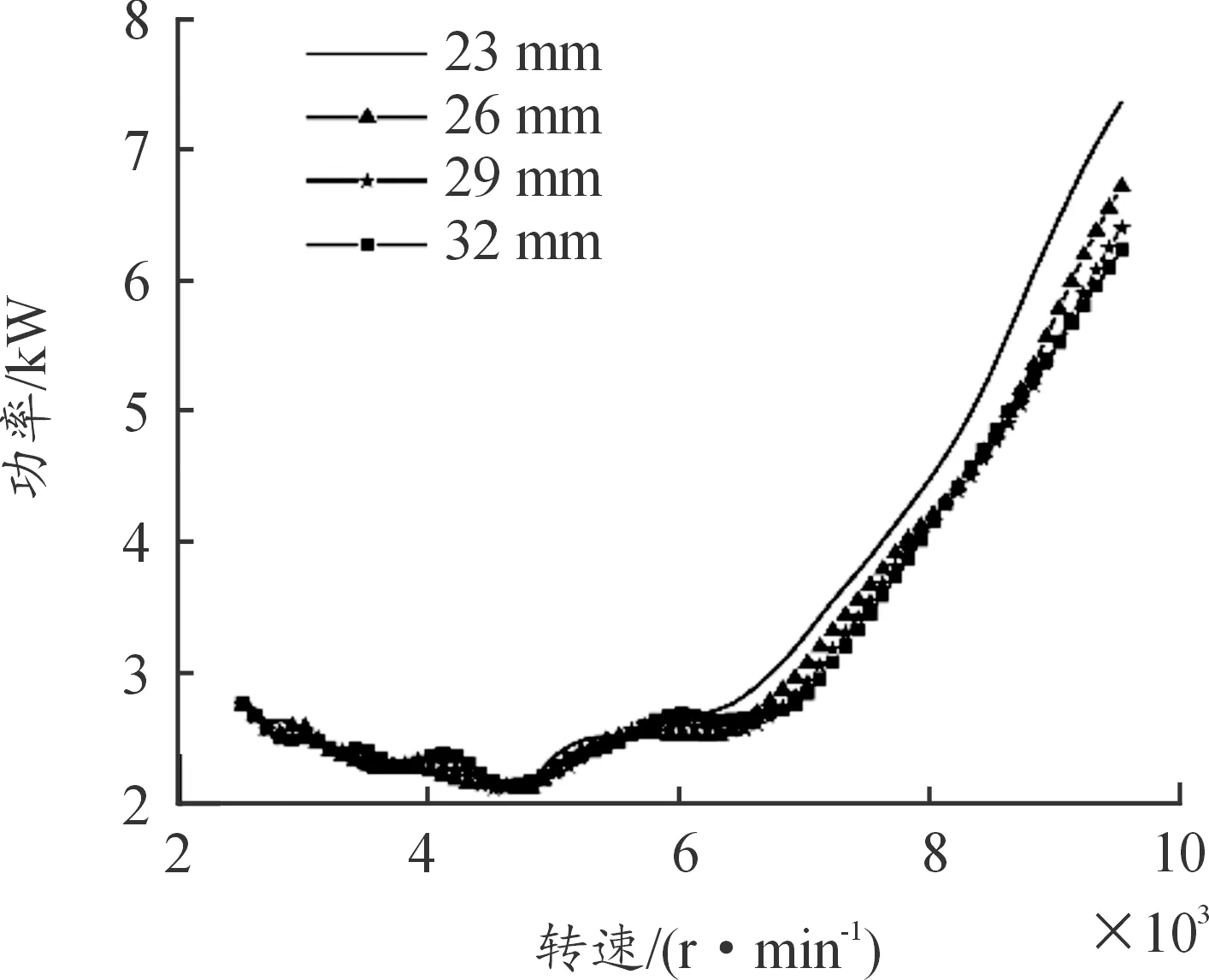
图11 进气管管径变化对比油耗的影响
3 进气管结构参数优化
以7 000 r/min为例,综合考虑发动机的经济性能和动力性能,联合遗传算法对未知系统非线性函数的拟合能力、神经网络算法对未知系统非线性函数寻找极值,对进气管的长度和管径进行参数优化。神经网络采用BP网络模型,其具有并行性、冗余性、自适应性优点,且网络只需要少量试验数据,经网络训练后就能反映发动机的特性,从而保障输出结果与实际过程的一致性。
3.1 神经网络遗传算法原理
神经网络遗传算法对进气管参数响应值寻优过程分为BP神经网络训练拟合和遗传算法搜索全局最优解[9]。其中,BP神经网络训练拟合包括BP神经网络构建、利用系统的输入输出数据对网络的处理功能进行训练和学习、实际响应值比油耗和扭矩的适应度函数输出的预测;遗传算法寻优的本质是进行有方向性且受概率引导的启发式计算。
对进气管结构参数进行拉丁超立方抽样,获取500组输入、输出数据值。BP神经网络的训练和拟合性能的测试需要在拉丁超立方抽样数据里再进行抽样,抽样方式为随机抽样,其中,用于网络训练的数据为450组。训练之后的BP神经网络可以代替与二阶响应面模型耦合的适应度函数,对该非线性函数模型的输入进行输出预测,并将神经网络预测的结果作为遗传算法中的染色体适应度值,适应度值越大,即目标性能越高,染色体越优秀。按照设置的中止条件对适应度值进行判断,若不满足迭代终止的条件,则根据选择操作决定下一代染色体。以初始化设置步骤中的概率,对染色体进行交叉策略、变异策略操作,再进行适应度判断。随着迭代次数的增加,目标性能较差的配气参数组合逐渐被淘汰,保留下来的配气参数组合个体目标性能优秀,配气参数组合逐渐向目标性能的最优方案收敛,迅速高效地搜寻到函数的全局近似最优解及对应的输入参数组合。
BP神经网络结构为2-5-1,即2个输入参数层、5个隐含层、1个输出参数层的网络结构设计。由于采用实数编码,个体长度为2;遗传算法中初始种群规模设置N=100,仿真程序迭代次数T=2 500,交叉概率Pi=60%,变异概率Pm=10%。当进化迭代数达到最大时,运算结束,输出优化目标结果,在仿真计算动态过程中完成进化。计算过程如图12所示。
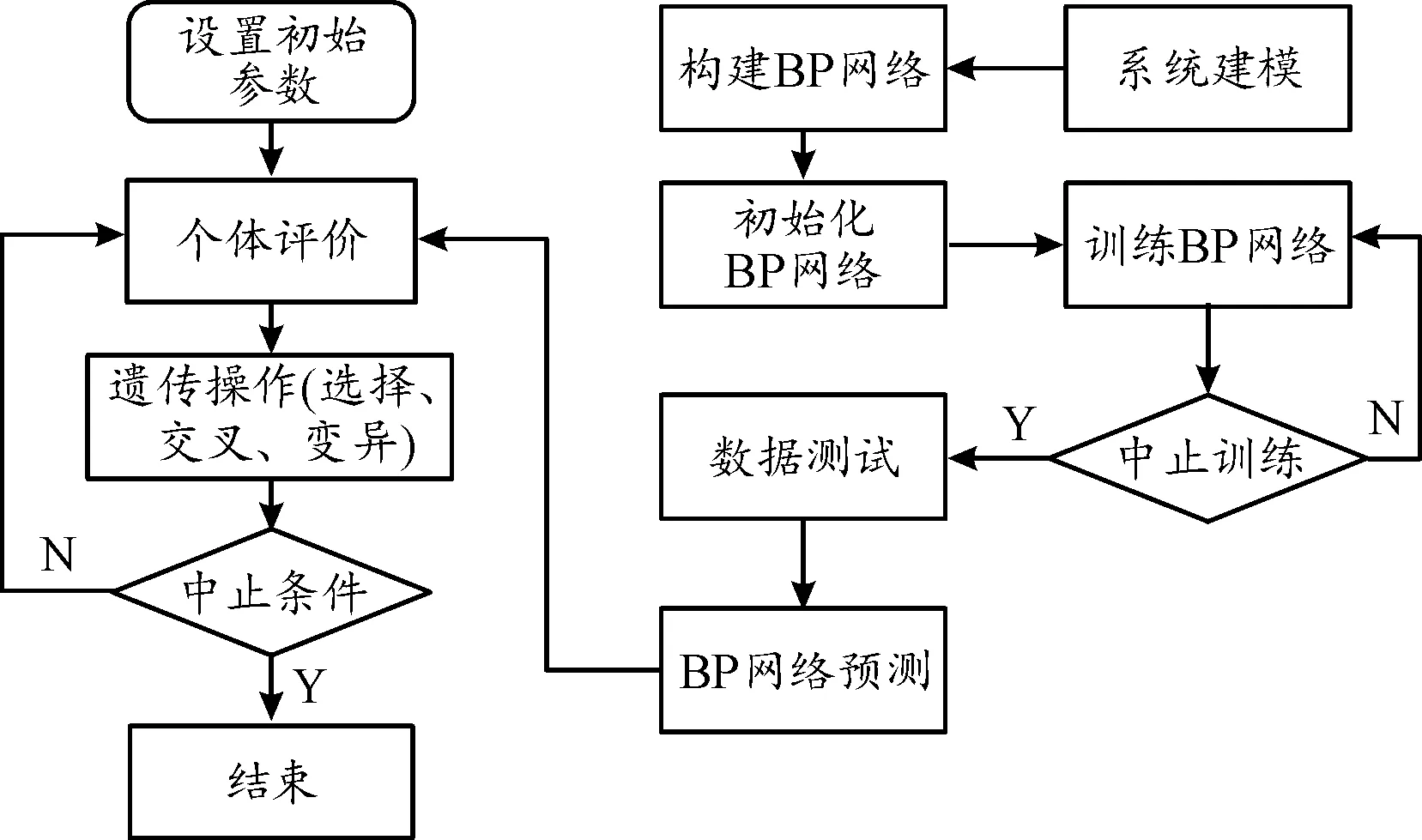
图12 神经网络遗传算法优化流程
3.2 针对优化目标构建适应度函数
基于神经网络遗传算法对进气管结构参数优化,同时考虑进气管长度和管径对经济性能和动力性能的影响。设计优化适应度函数由代表动力性能和经济性能的扭矩和比油耗2个性能指标以不同权重构成,如式(3)所示。扭矩最大化、比油耗最小化的优化目标转换为求适应度函数的区间极大值。
(3)
式中:T0和BSFC0分别为扭矩和比油耗性能指标的对比目标值,取前述抽样仿真实验结果的平均值作为对比目标值,其中T0为9.15 N·m,BSFC0为301.80 g·(kW·h)-1;L、D为进气管结构参数取值向量组;λ1和λ2为分配给2个响应目标的权重因子,不同的权重因子分配的值影响最终的优化结果。针对不同发动机的设计和工作要求,对发动机的性能取向要求不一致。文中使用的小排量高速汽油机在低转速时主要考虑其动力性能,而在高转速区间对经济性能有相对更高的要求,故此时分配给λ1、λ2两个权重因子值分别为20、5,不同转速下的权重因子可以重新分配取值。
3.3 神经网络遗传算法优化结果分析
BP神经网络输出预测和误差如图13—15所示,期望输出与预测输出的误差小,预测值可以近似成二阶响应面模型实际输出值。收敛结果如图16所示,适应度值在500代左右基本收敛至最优值。
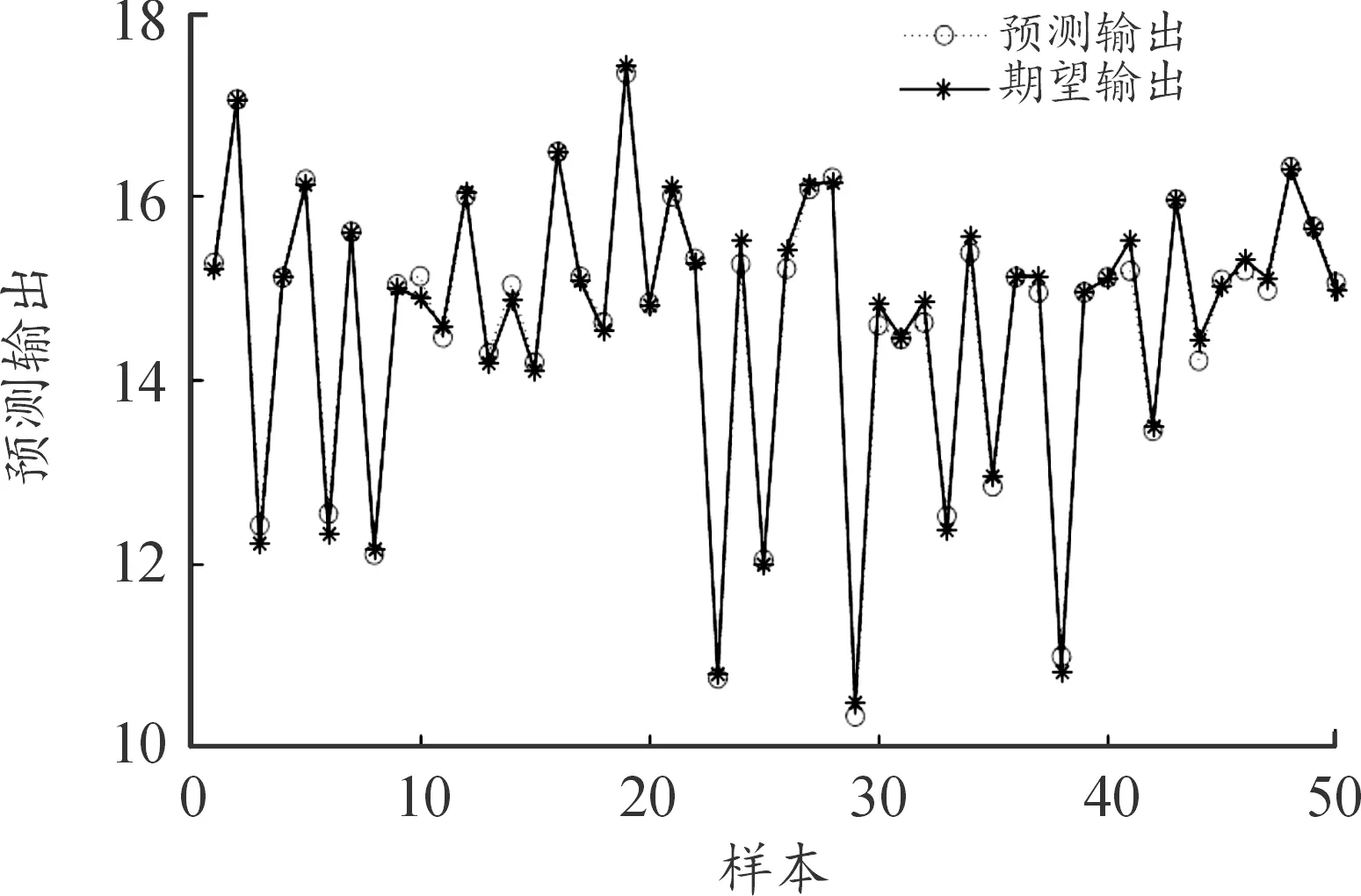
图13 BP网络预测输出
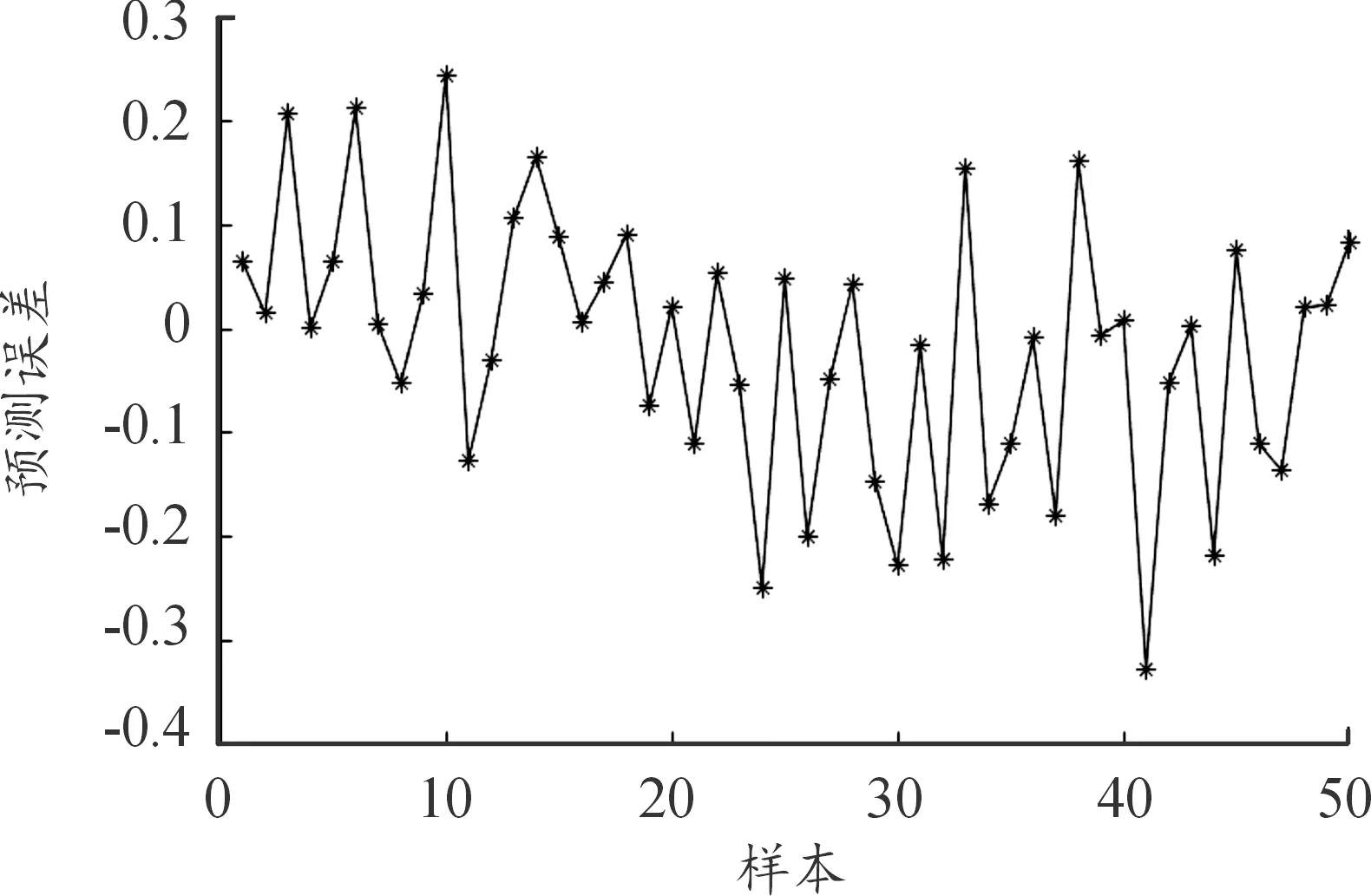
图14 BP网络预测输出的误差

图15 BP网络预测输出的误差百分比
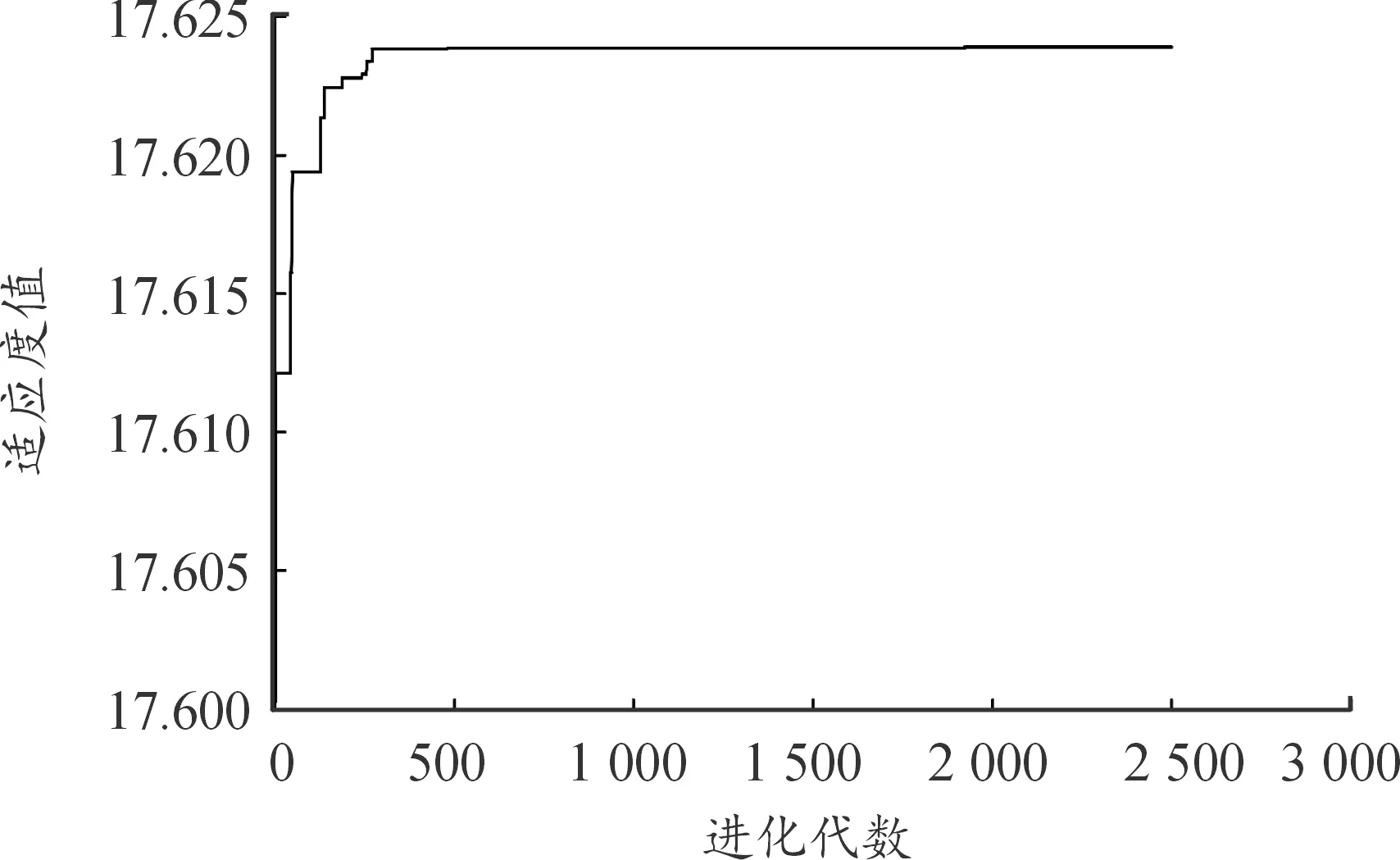
图16 适应度函数优化曲线
神经网络遗传优化过程是建立在抽样取值的基础上,与实际结果相比有一定偏差,因此需要验证预测优化结果。在发动机2 500、4 000、5 500、8 500 r/min分别进行算法应用,对不同转速设定不同扭矩和比油耗权重因子来满足不同的设计要求。采用优化后的配气参数,代入模型重新计算,表2为进气管参数优化后相应转速点的仿真实验值和实际优化效果值。采用新的进气管参数后,能够有效的提升动力性能和经济性能,同时也验证了模型的拟合程度、预测精度高。图17和图18为优化前后比油耗和扭矩的对比图。表2表明,在发动机4 000~5 500 r/min转速区间,扭矩的提升效果最明显,在发动机5 000~7 000 r/min转速区间,比油耗的提升效果明显。值得注意的是,发动机转速在2 500 r/min和8 000 r/min附近时,比油耗反而比原机的水平更高,扭矩提升效果较弱,这主要是因为这些转速下原机的进气管几何结构的经济和动力性能表现优异,原机的进气管尺寸较小适用于怠速区间和高转速区间,进一步降低进气管的长度和管径受到实际限制,因此优化空间也较小。
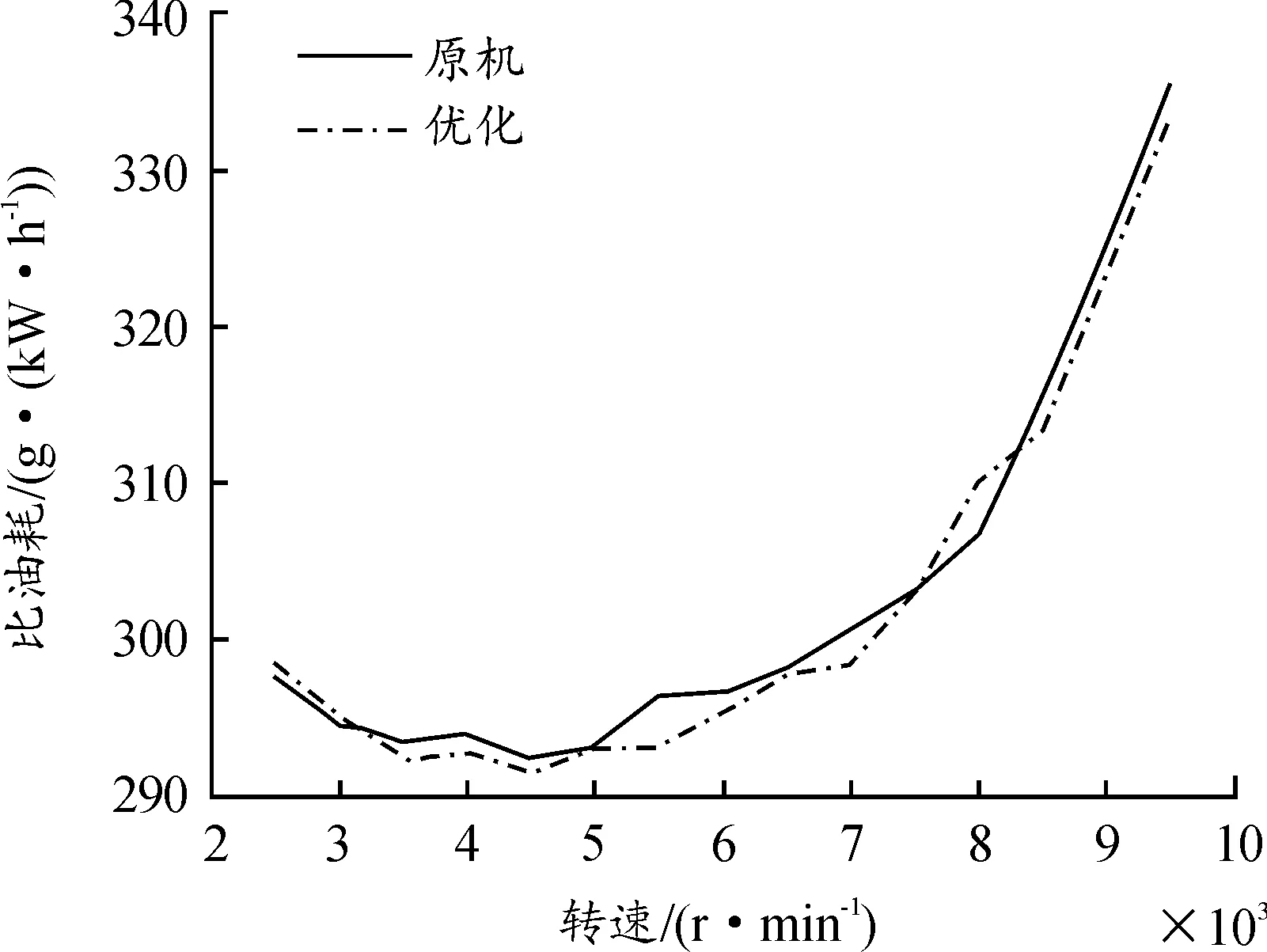
图17 比油耗优化对比图
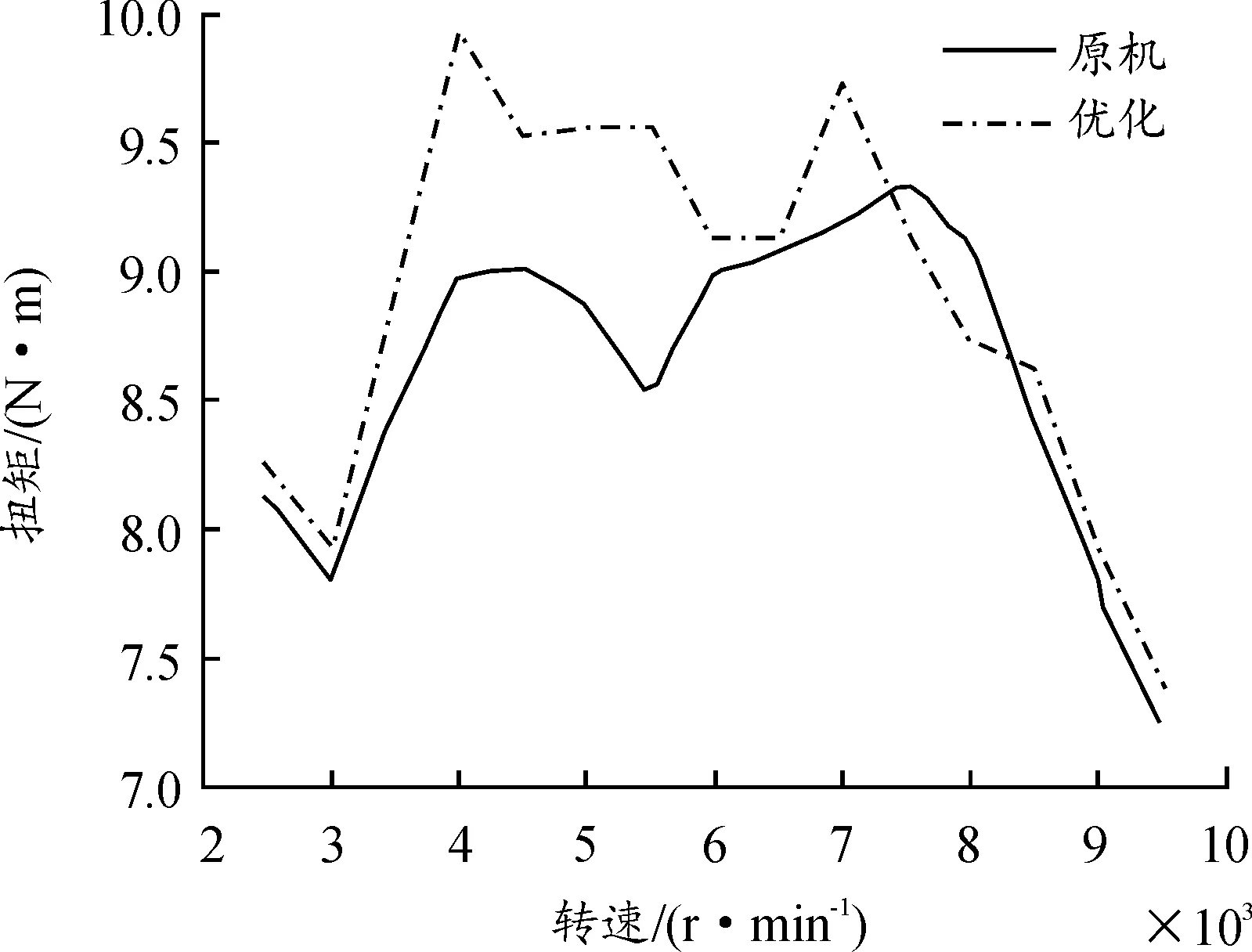
图18 扭矩优化对比图

表2 优化结果对比和验证
4 结论
结合某款高速汽油发动机为原型分析发动机进气管长度和管径参数对动力和经济性能的影响。在仿真系统模型的基础上,联合拟合函数遗传优化算法和神经网络遗传算法,设计外特性时不同转速时对应的最佳进气管结构参数,并得出如下结论。
1) 性能参数波动的幅度与进气系统结构参数、发动机转速有关。在中低转速下,适度增加进气管的长度可以使压力波的频率减小,波动的振幅提升,动态效应增强,改善充气效率;而在高转速下正好相反。
2) 进气管的管径对不同转速下的扭矩、功率和充气效率有较为显著的影响,进气管的管径变化主要通过影响进气气流的流速,进而对进气阻力以及沿程摩擦和能量损失产生影响。
3) 基于仿真系统模型,联合神经网络和遗传算法的应用,可实现发动机4 000~5 500 r/min转速区间扭矩的提升,发动机5 000~7 000 r/min转速区间比油耗的提升。在文中设定的优化设计目标下,扭矩优化率最高可达12.08%,比油耗优化率最高可达1.51%。
4) 针对进气管结构参数,通过集成一维仿真模型、神经网络遗传算法,并结合模型实验对比,可以获得发动机性能最优的进气管结构参数;集成方法的应用,对可变结构参数提供机理参考,可以为下一步可变结构设计提供依据。
